一种基于稀疏正则化的地下水点污染源识别法*
2020-10-20杨方浩吕中荣汪利
杨方浩,吕中荣,汪利
(中山大学航空航天学院,广东广州510006)
地下水是我国甚至全球重要的淡水资源之一,约占我国水资源总量的30%。而在我国部分城市,地下水几乎是唯一的供水水源[1]。由此可见,地下水资源具有一定的珍贵性。但是,我国地下水污染问题仍然相当严峻。并且,由于地下水具有隐蔽性和复杂性等特性,地下水污染的预防与治理工作十分困难。因此,通过已知的水文地质参数和监测点浓度数据,反求污染源位置及释放历史等信息具有十分重要的研究意义和实际价值。
地下水污染源识别属于典型的源项识别反问题,目的在于反演地下水污染源的位置及释放历史信息。然而,对于大多数反问题,往往是不适定的,即无法直接求解[2]。目前已有大量的研究通过正则化方法将地下水污染源识别问题转变为适定问题进行求解。Skaggs 等[3]将Tikhonov 正则化应用于地下水一维均匀流模型反问题中,在已知单个污染源的位置的情况下,反演得到污染源释放历史,进而得到污染物的时空分布。Li 等[4]在Tikhonov 正则化的基础上,提出了一种新的梯度正则化算法用于求解地下水一维均匀流的源项反演问题,有效地识别出线污染源的空间强度变化。Huang 等[5]通过共轭梯度法反演地下水二维均匀流模型中的线污染源空间变化强度。而邢利英等[6]通过改进的共轭梯度法重构地下水一维均匀流的线污染源空间释放函数。Onyari 等[7]对二维各向异性地下水含水层中的污染物运输反问题,通过格林函数法离散、奇异值分解及Tikhonov 正则化的最小二乘法等进行求解,重构了一维已知位点的污染源随时间变化的释放函数以及二维线污染源的空间变化强度,从而得到污染物的时空分布。Mazaheri 等[8]则是将格林函数法应用于一维对流−弥散方程,从而得到积分方程,并通过Tikhonov 正则化进行求解,以此准确地识别河流中的点污染源。Wang等[9]提出了一种基于有限元方法求解序列适定正问题的非迭代正则化优化算法,重构了地下水一维均匀流模型反问题中线污染源释放函数的空间变化。
综上可知,以上研究大多采用正则化方法对地下水非点污染源和已知点源位置情况下点源源强进行反演识别,也就是说目前采用正则化方法对地下水点污染源的空间位置识别研究较少。而已有研究是将稀疏正则化理论应用于空气污染源定位[10−11]、热源定位[12]以及声源定位[13]等领域。对此,本文将设计一种方法来识别地下水点污染源的位置及源强变化,即对反问题的目标函数引入l1范数项加以约束,然后利用交替优化算法分别迭代求解浓度场和源强。
1 地下水污染源反演模型
1.1 地下水污染物运移控制方程
假定承压含水层地下水的流动方向为x方向,且污染物为保守性污染物,初始浓度场为0,故采用不考虑吸附及化学反应的一维对流−弥散方程,为:
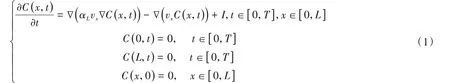
式中,T表示计算区域内的时间范围,L表示计算区域内的空间范围,C(x,t)表示污染物浓度,vx为沿x方向的地下水渗流速度,αL为纵向弥散度即沿x方向的弥散度,I表示源汇项。这里仅考虑点污染源,故有:



1.2 加稀疏约束的目标函数

1.3 交替优化法


1.4 正则化参数选取

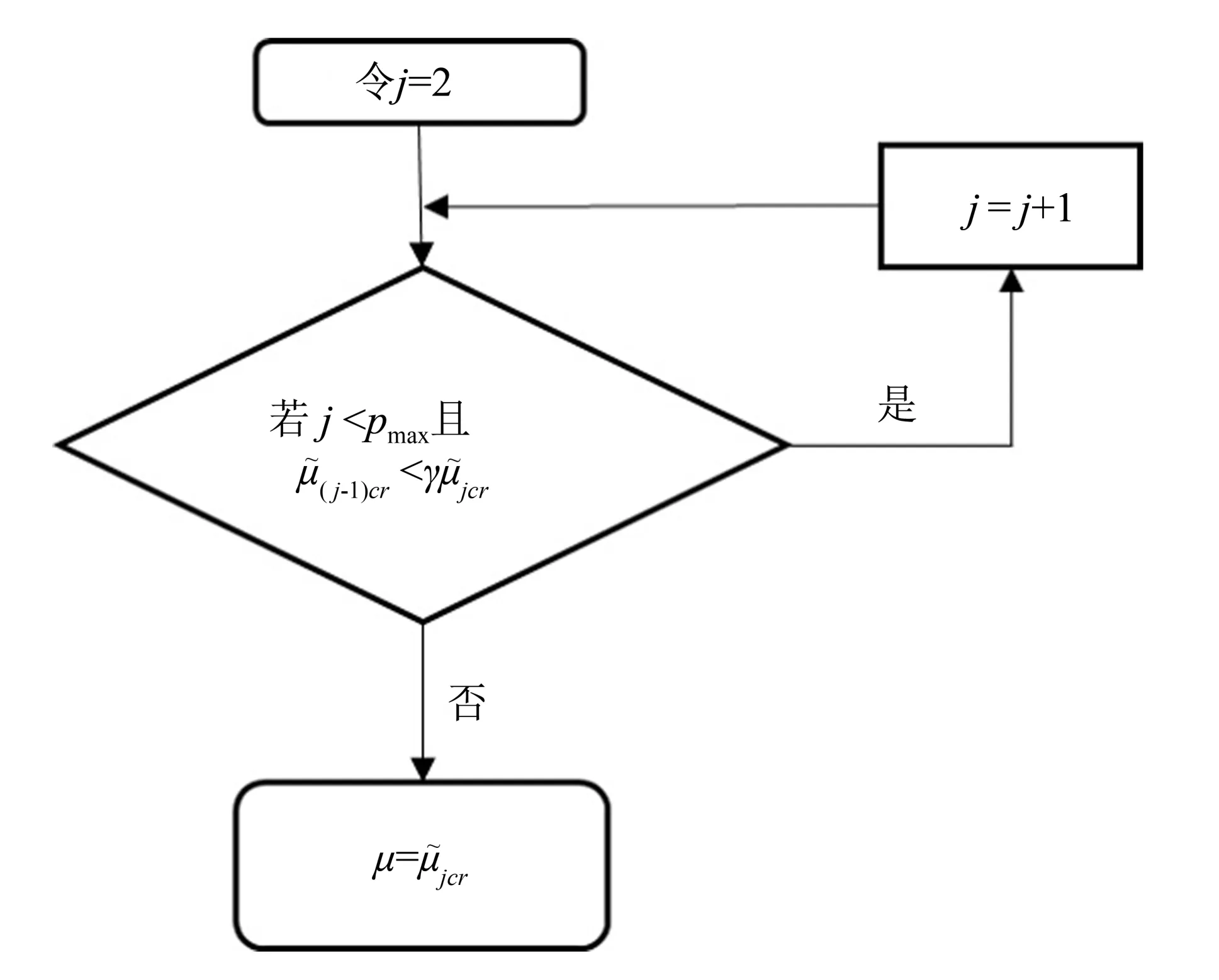
图1 正则化参数μ的选取Fig.1 Selection of regularization parameter μ
2 数值算例
本文研究一个一维的地下水污染源识别问题,如图2 所示。并令式(1)中,L= 100 m,T= 10 d,vx= 1m d,αL= 10 m,然后设空间步长为dx= 0.5 m,时间步长为dt= 0.01d,则将空间范围划分为200个单元,201个节点,并定义节点编号集合为{ni,i= 1,2,…,201},其中ni表示第i个节点上;单元编号集合为{ei,i= 1,2,…,200},其中ei则表示第i个单元内。
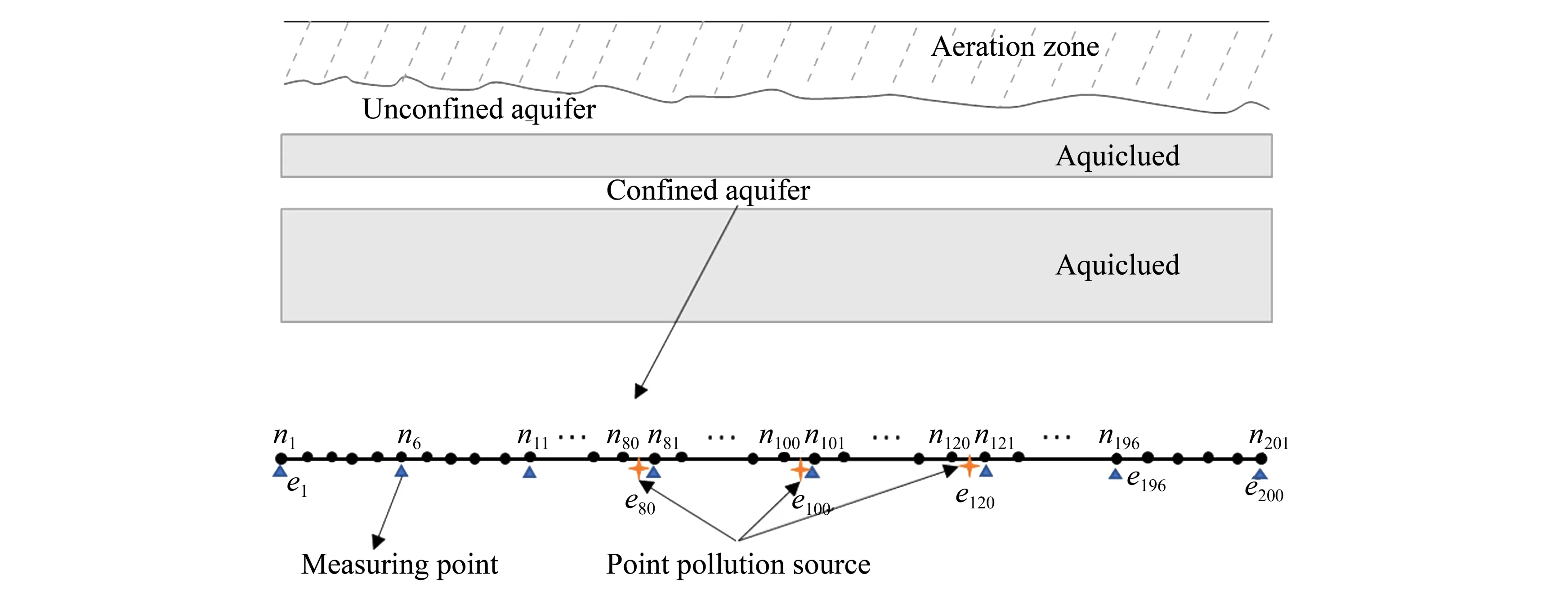
图2 一维地下水污染物运移示意图Fig.2 Schematic of a one−dimensional groundwater contaminant transport problem
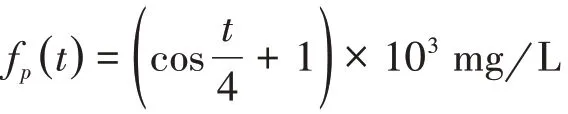
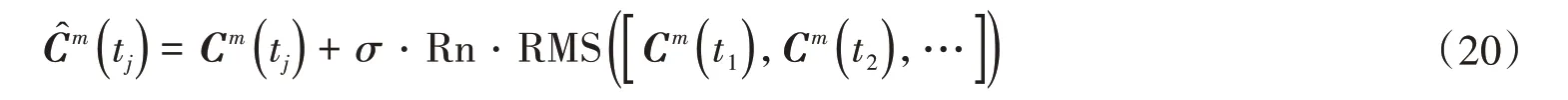
式中,Cm(tj)为上文所提的t时刻真实节点浓度,可由式(4)求得;σ表示噪声水平;Rn为由标准正态分布(即均值等于0,标准差等于1)求得的随机数;RMS表示均方根误差。

表1 一维点源识别的四种工况Table 1 Four scenarios for one−dimensional point sources identification

3 结 语
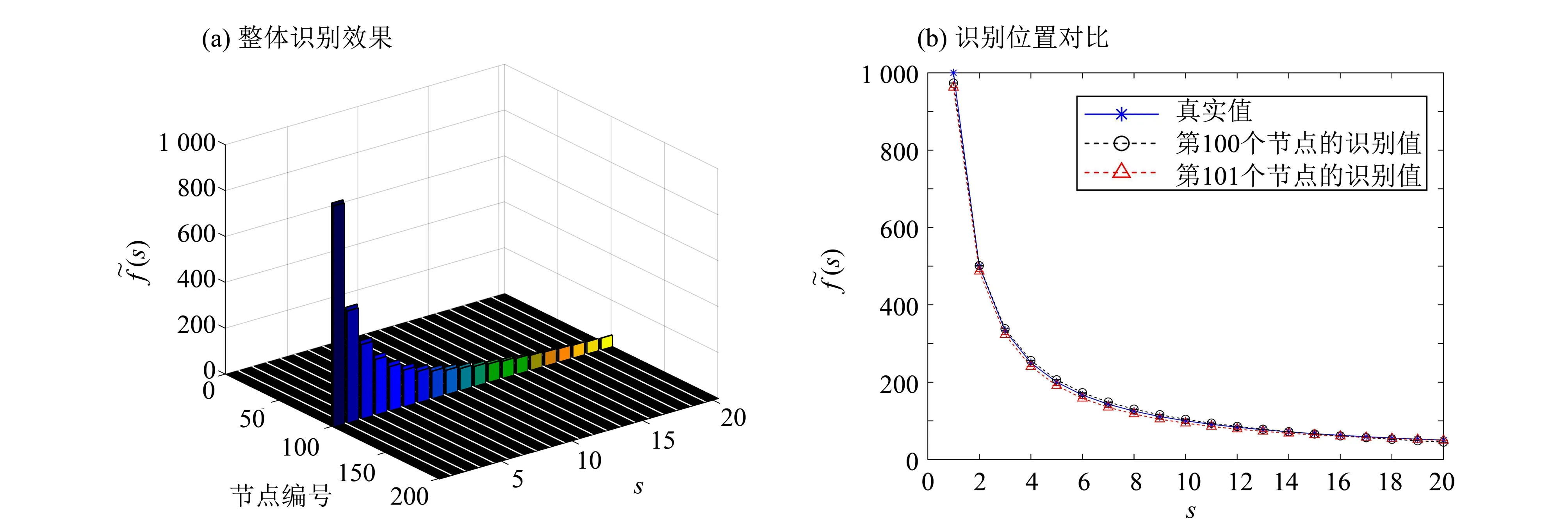
图3 工况1的稀疏正则化识别结果Fig.3 Identified results for scenario 1 with sparse regularization
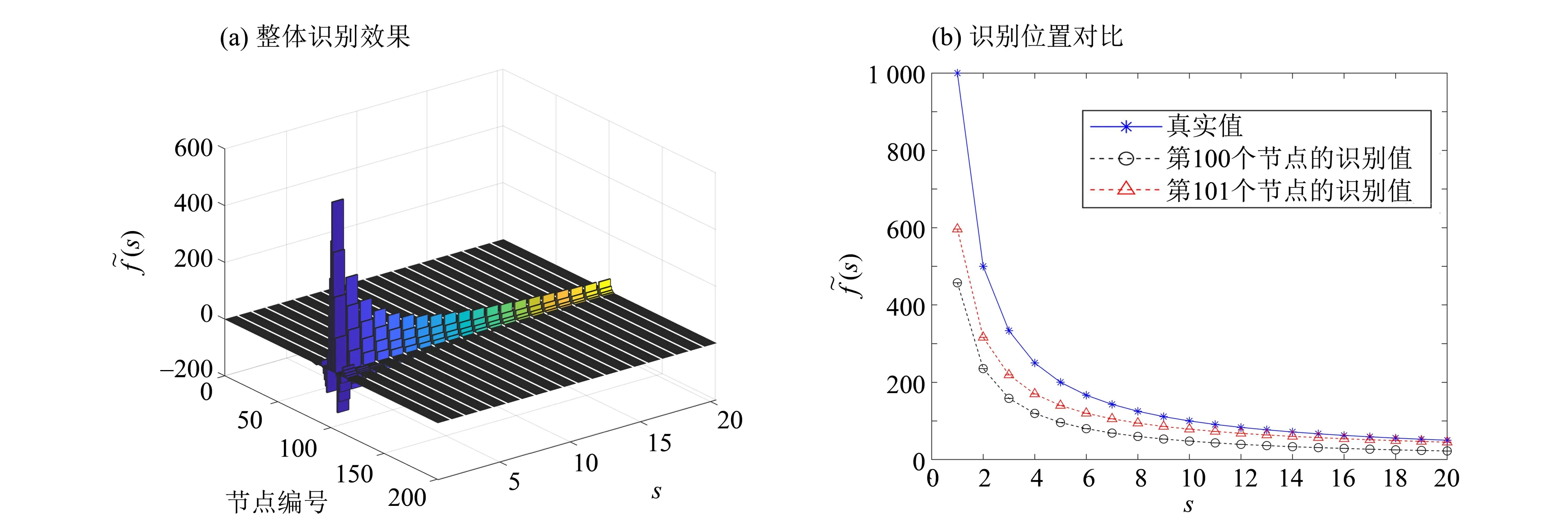
图4 工况1的无正则化识别结果Fig.4 Identified results for scenario 1 without regularization
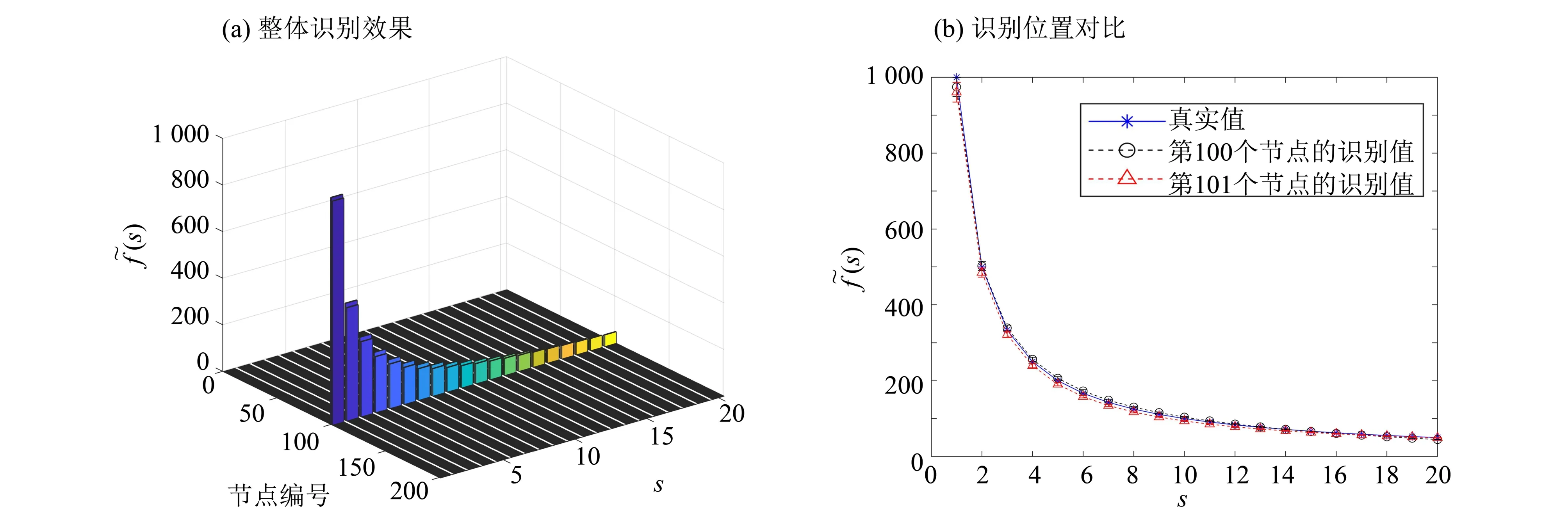
图5 工况2的稀疏正则化识别结果Fig.5 Identified results for scenario 2 with sparse regularization
针对地下水一维点污染源识别问题,本文提出了一种基于稀疏正则化的点源识别方法,从而为地下水污染的预防与治理工作提供一定的理论支持。首先,构造一维点污染源对流−弥散方程的时域有限元格式,并进行拉普拉斯变化得到频域方程,接着建立以l1范数项为约束的目标函数,从而克服污染源识别的不适定性并兼顾点源的稀疏性,然后利用交替优化法在不同噪声水平下进行迭代求解,发现所提方法能有效识别算例的点源位置及其强度变化,且其抗噪性较强,本论文方法可进一步推广应用到地下水二维点污染源识别问题。
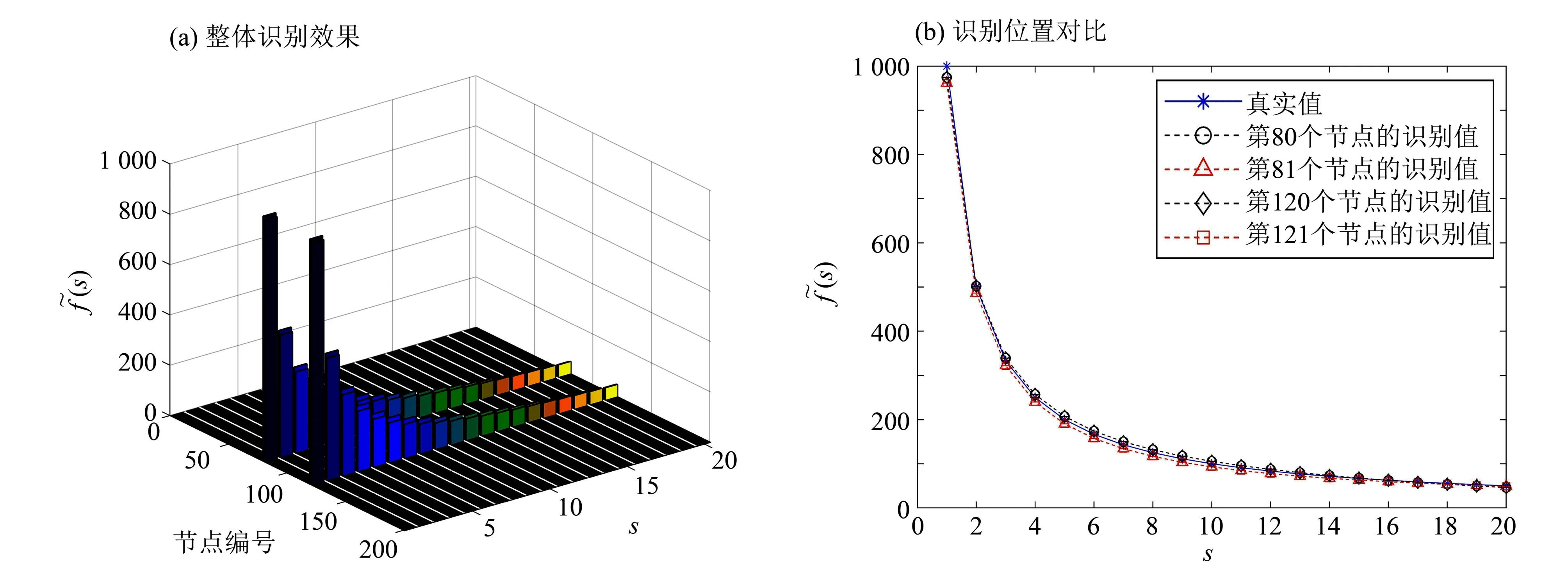
图6 工况3的稀疏正则化识别结果Fig.6 Identified results for scenario 2 with sparse regularization
图8 工况4的稀疏正则化识别结果Fig.8 Identified results for scenario 4 with sparse regularization
