卡拉比-丘代数的导出表示概型与平移泊松结构*
2020-10-20陈小俊陈友明艾西玛多夫艾西玛多夫
陈小俊,陈友明,A. 艾西玛多夫,F. 艾西玛多夫
(1. 四川大学数学学院,四川成都610064;2. 重庆理工大学理学院,重庆400054;3. 托莱多大学数学与统计系,美国俄亥俄州托莱多43606;4. 首都师范大学北京成像理论与技术高精尖创新中心,北京100048)
在代数几何中,仿射概型(affine scheme)组成的范畴与交换代数组成的范畴是等价的。在此对应下,一个几何对象(或者结构)可以用代数的语言来描述,反之亦是如此。例如,仿射概型上的向量丛等价于对应的交换代数上的有限生成投射模,概型上的切向量场等价于对应的代数的导子(derivation),等等。
像投射模、导子这些概念,不仅仅对交换代数可以定义,它们对一般的结合代数也是可以定义的。一个自然的问题是:对于一个结合代数,是不是也存在类似“仿射概型”这样的空间,使得上面这些代数的概念可以对应到相应空间的几何结构上?
在过去几十年中,数学家们一直在寻找这样的空间,但是并不是很成功。虽然如此,我们仍然可以假想这些空间是存在的,并称之为“非交换空间”,这些非交换空间上的几何称为“非交换几何”。实际上,我们在研究几何结构的时候,往往是通过这些几何结构与其他已知空间上的几何结构的关系来得到相应的信息。如果我们收集的这种信息足够多,那么“窥一斑而知全豹”,这个假想的“非交换空间”的各种几何性质也就足够清楚了,或者更准确地说,对我们的研究而言,就已经足够了。
1 背景介绍
本文接下来从所谓的Kontsevich−Rosenberg 原理出发,以非交换泊松几何和非交换辛几何为例,介绍非交换几何的研究思想、内容和方法。
我们需要指出的是,导出非交换代数几何是一个非常宏大的研究领域,囿于作者的学识,我们甚至不能对这一领域做一个大概的介绍。在本文中,我们只对我们感兴趣的几个问题做一个简介。读者们不要误认为导出非交换几何仅限于我们文中介绍的几个专题。
1.1 Gelfand−Naimark定理和Gabriel定理
一般认为,非交换几何的研究肇始于Gelfand−Naimark 定理。设M是一个局部紧致的Hausdorff 拓扑空间。我们记C(M)为M上复值连续函数组成的集合,可以证明它是一个交换的C*代数。1943 年,Gelfand和Naimark 证明了:一个交换的C*代数决定一个拓扑空间(作为集合,它由该C*代数的极大理想组成),使得该代数同构于这个拓扑空间上的复值连续函数。也就是说,M和C(M)互相决定对方。一般情况下,一个C*代数不一定是交换的,那么我们有没有类似的Gelfand−Naimark 定理呢?菲尔兹奖获得者Connes 创立的非交换微分几何说:对于不交换的C*代数,我们可以假想存在一个空间,使得上面的Gelfand−Nai⁃mark 定理“理论上”成立;特别是在做一些计算的时候,我们在很多时候并不需要关注这些C*代数是否来自于一个真实的空间。该假想存在的空间,一般就称为“非交换空间”,其上的微分几何,就是“非交换微分几何”。
在Grothendieck 学派的代数几何研究中,Gabriel证明了一个类似的定理:两个概型同构当且仅当它们的凝聚层范畴是等价的。也就是说,概型的凝聚层范畴完全决定了这个概型本身。例如,概型的K−理论,它是凝聚层的不变量,因此要研究K−理论,我们只要知道凝聚层就够了。
遵循Grothendieck 学派的这一思想,在1990年代,Artin和Zhang在非交换几何领域做出了极富价值的探索。他们以及很多数学家们如Tate、Smith、Van den Bergh 的工作,成为了数学的一个研究分支,被称为“非交换射影几何”。
1.2 Kontsevich−Rosenberg原理
在2000 年左右, 菲尔兹奖获得者Kontsevich 和Rosenberg 提出了一个研究“非交换代数几何”的原理[1]:对于一个非交换空间(在本文中,我们把它等同于一个结合代数;我们将会看到,实际情形不限于此),其上的非交换几何结构(例如我们下面要讨论的非交换辛结构、非交换泊松结构等),如果存在的话,它一定诱导该代数表示概型(representation scheme)上的经典几何结构(即通常的辛结构、泊松结构等)。
这一原理现在被人们称为Kontsevich−Rosenberg 原理。那么,为什么要提出这个原理呢?它的道理何在?
要回答这个问题,我们需要回到文章开始提到的“交换代数−仿射概型”对应。对于一个交换代数A,它对应的仿射概型是A的素理想组成的集合(谱),称为素谱,记为SpecA。稍微熟悉代数几何的人都知道,SpecA中真正与我们所熟知的“点”对应的是A的那些极大理想,记为SpmA。这些极大理想组成的集合同构于
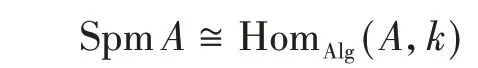
而后者又可以看成A的一维表示组成的集合。
现在,如果我们令k是代数闭域,那么表示论告诉我们,A的所有不可约表示都是一维的。也就是说,在此情形下,A本质上没有高维的表示。但是,如果A是一个结合且非交换的代数,则情况大不相同:A存在非平凡的不可约高维表示!
从这个观察,我们可以认为:对于一般的结合代数,它对应的“素谱”(或者更准确地说,极大理想组成的谱),应该是它所有的表示组成的集合。如果我们记Repn A为A的n维表示组成的集合(容易证明,这是一个仿射概型),那么
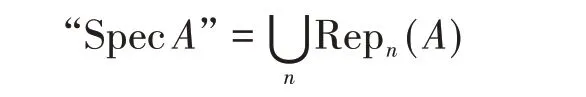
由此,我们得出:结合代数A所对应的“非交换空间”(也即我们要找的“SpecA”)上的几何结构,一定会反映到Repn(A)上;反之,如果对所有n,Repn(A)上都自然地存在一个几何结构,我们就说A上存在相应的非交换几何结构。这就是Kontsevich−Rosenberg原理提出的背景。
1.3 Kontsevich−Rosenberg原理的应用
Kontsevich−Rosenberg 原理是一个十分美妙、十分深刻但同时也是非常粗略的原理。它给出了一个寻找非交换几何结构的指导原则,但并不能给出一些非交换几何结构的具体刻画。虽然如此,它仍然极大地激发了人们的研究兴趣,并努力地寻找符合这一原理的“非交换几何结构”。
在2009 年左右,英国数学家Crawley−Boevey[2]、比利时数学家Van den Bergh[3]各自给出了一个版本的“非交换泊松结构”的定义;与此同时,Crawley−Boevey 和美国数学家Etingof、Ginzburg 一起定义了“非交换辛结构”[4]。
在第2 小节中,我们将给出这些结构的具体定义。从Crawley−Boevey 等的工作中,我们可以观察到“喜忧参半”的两点:
(i)对于一般的结合代数A,Repn(A)是一个不光滑的仿射概型,因此要刻画其上的通常几何对象如微分形式、切向量场等等,都是非常困难的;
(ii)对于自由的结合代数,Repn(A)又是相当简单的,就是多项式的素谱,因此其上的几何对象很容易给出。
这两点促使康奈尔大学的数学家Berest等思考如下问题:对于一般的结合代数A,能否找自由的结合代数来逼近A,从而得到相应的多项式来“逼近”Repn(A)?如果我们扩大研究的范畴,考虑“微分分次结合代数”组成的范畴,那么,上述问题的答案是可能的。Berest 等[5−6]的结果说:一个结合代数A,总存在一个自由的微分分次代数的逼近,与此同时,该逼近也给出了Repn(A)的自由的微分分次交换代数的逼近。该Repn(A)的充分逼近,被Berest等称为“导出表示概型”(derived representation scheme)。当然这些“逼近”,并不是任意的,而是基于1960 年代菲尔兹奖获得者Quillen 发展的“有理同伦论”(Ratio⁃nal homotopy theory)。
1.4 Berest等的导出表示概型
根据有理同伦论,特征为0 的数域k上的微分分次结合代数组成的范畴,记成DGA,具有“模型范畴”结构,因而每一个结合代数(把它看成具有0微分的微分分次代数)可以由一个自由的微分分次结合代数来逼近,也就是存在一个“预解”(resolution)
(QA,d) →A
其中d是微分,使得同调群H.(QA,d) ≅A,并且这个逼近是内蕴的、在相差一个同伦的意义下是唯一的。
类似地,数域k上的交换微分分次代数组成的范畴,记作CDGA,作为微分分次结合代数的子范畴,也具有“模型范畴”结构,因而每一个交换代数也可以由一个自由的、交换的微分分次代数来逼近。
这两个范畴在拟同构下的局部化,称为它们的同伦范畴。现在将Repn(A)与其对应的交换代数等同,Berest等[5]证明函子
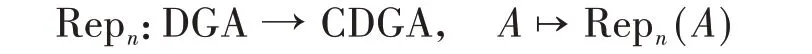
可以提升到两者的同伦范畴上。直观地说,对于一个结合代数A,如果QA是它的一个自由逼近,那么Repn(QA)就是Repn(A)的一个“充分好”的逼近。
当然,在这里我们需要证明,对于微分分次代数,Repn(A)也是有意义的,但这并不困难。Berest等称Repn(QA)为A的“导出表示概型”。
利用导出表示概型,我们可以将Crawley−Boevey 等的构造推广到微分分次代数的同伦范畴,从而非常轻松地构造一大类(导出意义下的)非交换的泊松结构和非交换的辛结构。
我们需要注意到一点是:我们这里所有的构造都需要将“微分分次”这个条件考虑进去。例如在研究导出的非交换辛结构时,我们需要构造“切空间”与“余切空间”的同构,如果把微分分次这样条件考虑进去,我们需要将其中一个空间(实际上是链复形)进行一定的平移,才能得到同构(或者拟同构)。这样的辛结构称为“平移辛结构”(shifted symplectic structure)。类似地,我们也有“平移泊松结构”的概念。
1.5 卡拉比−丘范畴与卡拉比−丘代数
假设X是一个卡拉比−丘射影代数簇。我们考虑X上的有界凝聚层范畴的导出范畴,记为D(X)。由于X的典则层(canonical sheaf)是平凡的,因此D(X)上的Serre 函子是恒同函子。对于任意两个凝聚层ℰ,ℱ,我们有Serre对偶定理:

如果我们令ℰ = ℱ,Toën 等[7]的结果说,HomD(X)(ℰ,ℰ),作为分次线性空间在相差一次平移下,可以看成D(X)中凝聚层组成的模空间在ℰ 处的切空间,因而同构(1)可以看成切空间和余切空间的一个同构(在相差(2−n)次平移下)。由此,我们可以得到一个结论:D(X)的模空间上存在一个平移辛结构。
当然,具有同构(1)的三角范畴是很多的,这样的范畴称为“卡拉比−丘范畴”(Calabi−Yau catego⁃ry)。很多的卡拉比−丘范畴等价于一个结合代数的模范畴的导出范畴,这样的结合代数在很多情况下是“卡拉比−丘代数”(Calabi−Yau algebra)。由此,我们得到一串构造:
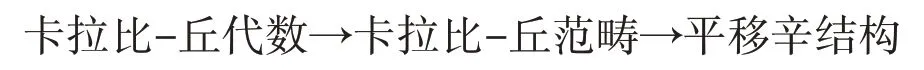
一个自然的问题是:卡拉比−丘代数上的什么结构导致了其(模范畴的)导出范畴上的平移辛结构?这个问题的答案,如果存在的话,可以看成是Kontsevich−Rosenberg原理的推广。
在接下来的小节里,我们将对上面出现的这些概念和结果进行进一步的介绍。
2 非交换辛结构和非交换泊松结构
在物理学中,辛结构和泊松结构是最基本的概念之一,它们最初出现于19 世纪Poisson、Hamilton 和Jacobi 等关于理论力学的研究当中,并由此获得了人们广泛的研究。到了20 世纪80 年代,数学和物理又进入了一个大融合的时代,新的理论、新的结构层出不穷。例如物理学中的杨−米尔斯理论、超弦理论,被很多数学家进行了深刻的研究,数学中的纽结理论、陈−西蒙斯理论等等在物理中亦有重要的应用。
在这些理论层出不穷的同时,有识之士如Kontsevich、Sullivan 等亦在不断地反思,去芜存菁,发掘、总结这些看上去毫不相关的理论背后的共同点,并通过演绎类比,探索、发现一些往往被人忽略了的新的结构。
例如,对于我们耳熟能详的泊松结构、辛结构,经过200多年的发展,我们几乎不能够期望再有什么新的发现了。但是,通过发展导出的非交换代数几何,将这些经典的概念作为这种新的几何的特殊情形,我们不仅对这些概念有了全新的理解,而且通过将很多新出现的概念,如我们将要谈到的凝聚层范畴、Fukaya范畴等纳入这一范畴之中,这些古老的概念获得了新的内涵,焕发了新的生机。
下面,我们将从泊松代数的概念出发,开始我们的导出非交换代数几何的探索之旅。
定义1(泊松代数) 设A是一个交换结合代数。如果A上存在着一个对每个分量都满足Leibniz法则的李括号{−,−},即对于任意的a,b,c∈A,

那么我们称A为一个泊松代数。
当代数A仅仅是一个结合代数而不具有交换性时,若我们仍然按照刚才的定义来定义A上的泊松代数,则Farkas和Letzter在文[8,Theorem 1.2]中证明了下列结论。
定理1设A是一个非交换的整环,或者更一般地,是一个非交换素环。若A上有李括号{−,−}满足Leibniz法则(2),则存在一个A的中心元λ使得
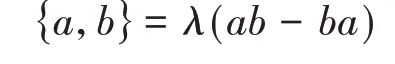
也就是说,若按照上面这种直接的方法定义非交换泊松结构,则李括号本质上由交换子给出,因此这一定义给出的非交换泊松结构是没有太大的意义的。在下面的几小节里,我们介绍几种版本的非交换泊松结构和辛结构,它们分别是:Crawley−Boevey 的H0−泊松结构,Van den Bergh 的双泊松结构(double Poisson structure),以及Crawley−Boevey,Etingof 和Ginzburg 提出的双辛结构(bi−symplectic structure),并指出它们之间的联系。
2.1 Crawley−Boevey的H0−泊松结构

注记1(i)Crawley−Boevey 称上述概念为H0−泊松结构的主要原因是因为A[A,A]实际上是A的0−维Hochschild(也是循环)同调群。后来,Berest 等将这一概念推广到导出代数几何中,这就涉及到所有的循环同调群了。
(ii)在上述定义中,如果A是交换的,我们可以看到:H0−泊松结构就是通常的泊松结构。在这个意义下,H0−泊松结构可以说是交换代数的泊松结构的非交换推广(在§2.6我们将讨论泊松结构的非交换推广的另一个版本)。
Crawley−Boevey在文章中证明:
定理2([2]Theorem 1.6) 设A是特征为0的数域k上的一个结合代数。如果A上存在一个H0−泊松结构,则
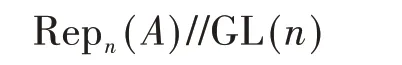
上存在着一个自然的泊松结构。
这个定理主要用到了Procesi的一个结论:考虑“迹映射”
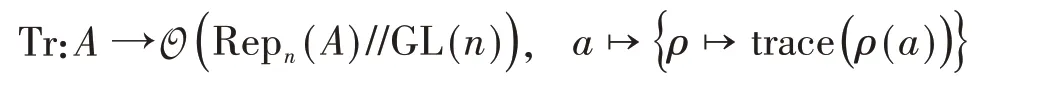
其中ρ∈Repn(A),则Tr的像生成O( Repn(A)//GL(n) )。我们很容易在Tr的像集上定义一个李括号,并且利用H0−泊松结构中的导子性质,把这个李括号定义到整个Repn(A)//GL(n)上使之成为一个泊松代数。
我们注意到,这个H0−泊松结构非常好地符合了Kontsevich−Rosenberg原理。
2.2 Van den Bergh的双泊松代数
大约与Crawley−Boevey 同时,Van den Bergh 在文[3]中引进了“双泊松结构”(double Poisson struc⁃ture)。
定义3(Van den Bergh) 设A是一个带幺元的结合代数。A上的一个双括号(double bracket)是一个双线性映射{{−,−}}:A⊗A→A⊗A使得
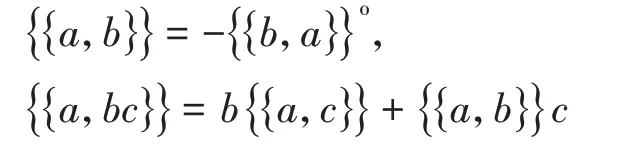
其中(u⊗v)o=v⊗u。这里b和c的作用是由A⊗A的双模结构给出的,即:b(a1⊗a2)c:=ba1⊗a2c。
设{{−,−}}是A上的一个双括号。任取a,b1,…,bn∈A,s∈Sn,记
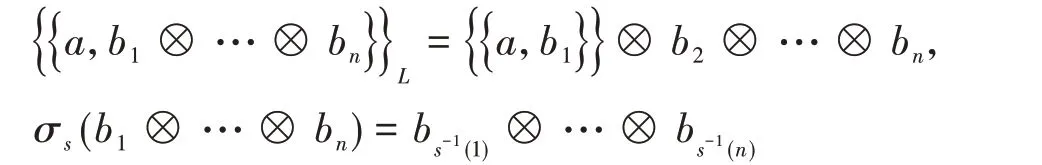
则A上的一个“双泊松结构”(double Poisson structure)是一个满足“双雅可比恒等式”(double Jacobi identity)的双括号{{−,−}},即对于任意的a,b,c∈A,
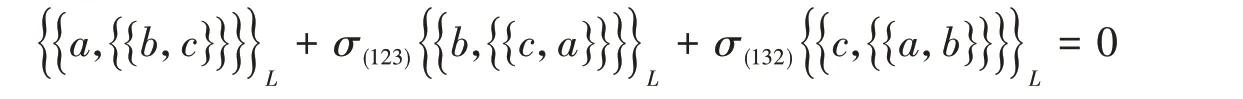
类似地,Van den Bergh证明了以下定理:
定理3([3] Proposition 7.5.2) 设A是一个结合代数。如果A上存在一个双泊松结构,则Repn(A)上存在一个自然的泊松结构。
Van den Bergh 的这个定理也非常好地符合了Kontsevich−Rosenberg 原理,它与Crawley−Boevey 定理的区别是:这两种非交换泊松结构诱导的泊松结构,一个是定义在Repn(A) 上,一个是定义在Repn(A)//GL(n)上。
2.3 Crawley−Boevey,Etingof和Ginzburg的双辛结构
在本小节,我们讨论Crawley−Boevey,Etingof 和Ginzburg 在文[4]中提出的“双辛结构”(bi−sym⁃plectic structure)。

通过莱布尼茨法则,导子d诱导了Ω.A上的导子d。从而(Ω.A,d)是一个微分分次代数。然而,对于带幺元的结合代数A,(Ω.A,d)的同调却总是平凡的:
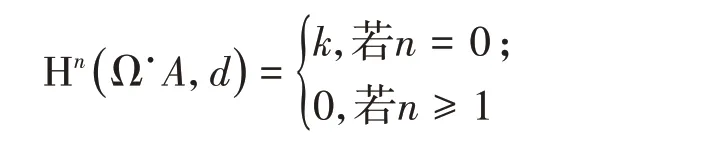
但是,A的Karoubi−de Rham 复形
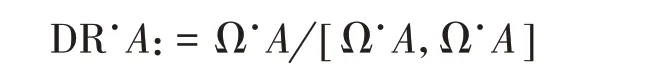
有非平凡的同调群,其上的微分由DR.A上的微分d诱导而来。
注意到Ω.A是Ω1A在A上的张量代数,因此缩并算子ῖΘ:Ω1A→A⊗A诱导了分次代数Ω.A的一个度数为−1 的“双导子”ῖΘ,即ῖΘ∈Der(Ω.A,Ω.A⊗Ω.A)。更确切地说,任意给定α1,α2,…,αn∈Ω1A,我们有
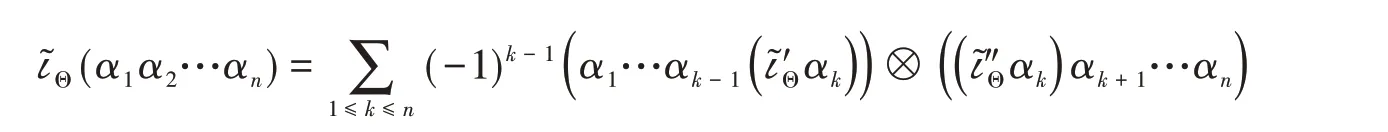
下面,我们令
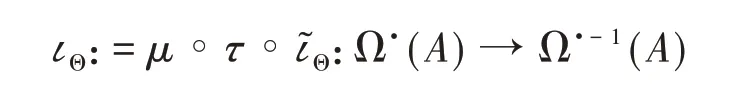
其中μ是乘积,τ:a⊗b↦(−1)|a||b|b⊗a是置换算子。特别地,对于ω∈Ω2A,我们得到映射
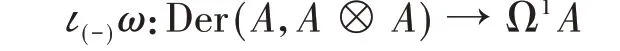
容易看出,这一映射仅仅依赖于ω在DR2A中的等价类。
定义4(Crawley−Boevey−Etingof−Ginzburg) 设A是一个结合代数。A上的一个双辛结构(bi−symplec⁃tic structure)是指A的一个满足以下条件的闭2−形式ω∈DR2A:映射

是A−双模同构。
Crawley−Boevey,Etingof和Ginzburg证明了他们引进的该双辛结构也满足Kontsevich−Rosenberg原理:
定理4([4]Theorem 11.3.1) 设A是一个结合代数。如果A上存在一个双辛结构,则对于任意的自然数n,Repn(A)上有一个辛结构。
2.4 以上三种非交换结构之间的关系
上面3小节介绍的三种非交换几何结构之间的关系是非常密切的。Van den Bergh在文[3]中证明:
2.4.1 双泊松结构蕴含H0−泊松结构
设(A,{{−,−}})是一个双泊松结构。记A上的乘法为μ,并令
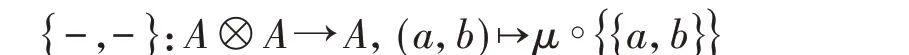
根据双泊松结构的定义,固定{−,−}中的一个元素,则括号对另一元素相对于乘法都是一个导子。Van den Bergh 证明(由计算可以直接得到):{−,−}可以下降到A♮:=A[A,A]上成为其上的一个李括号。由此,我们可以得到
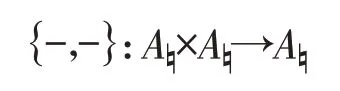
是一个H0−泊松结构。
2.4.2 双辛结构蕴含双泊松结构
设(A,ω)是一个双辛结构。则对于任意的a∈A,存在着对应的哈密顿向量场Ha∈Der(A,A⊗A)使得ιHa ω=da。若令

则{{−,−}}ω是A上的一个双泊松结构;证明见文[3]附录。
2.5 箭图代数的例

其中
则(P,ω)是一个双辛结构[4]。
2.6 另一种非交换泊松结构
在1990年代,Block−Getzler[9]和宾夕法尼亚州立大学的徐平教授[10]分别给出了另一种非交换泊松结构的定义。
定义5(徐平,Block−Getzler) 设A是一个结合代数。A上的一个“非交换泊松结构”是指A的一个Hochschild上同调α∈HH2(A)满足
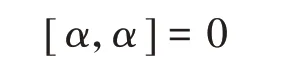
如果我们记Z(A)为A的中心,则Z(A)是A的一个交换的子代数;反之,我们可以把A看成交换代数Z(A)的非交换扩张。现在假设α是一个非交换泊松结构,那么α诱导了Z(A)上经典意义下的泊松结构(见文[10,Proposition 2.1])。在这个意义下,定义5 给出的非交换泊松结构也是泊松结构在结合代数范畴上的推广。这种非交换泊松结构曾被Getzler和唐翔等仔细研究过。
另一方面,我们难以看到这种非交换泊松结构满足Kontsevich−Rosenberg 原理。话又说回来,注意到Hochschild 上同调是结合代数的导出不变量,因此这种非交换泊松结构可以在结合代数的同伦范畴下定义;与此同时,Crawley−Boevey 的H0−泊松结构也可以在结合代数的同伦范畴下考虑。我们可以看到,在同伦范畴下,这两个版本的非交换泊松结构,实际上是统一的,具有很好的函子性,它们分别是导出意义下“多重切向量场”的Maurer−Cartan方程的解的一个分支。我们将另文做详细的讨论。
注记2 在本小节,我们详细地介绍了非交换几何而不是“导出代数几何”的几个例子。这样做的原因是:我们首先要对经典的几何有充分的了解,然后才能在导出代数几何中有迹可循而不致迷失。
3 表示概型与Van den Bergh函子
在本小节,我们稍加详细地讨论表示概型上的几何结构。特别地,我们讨论如何将一个结合代数上的非交换几何结构转化到它的表示概型上。
3.1 表示概型
设k是一特征为0 的数域,A是一个带幺元的k−结合代数,V是k上的线性空间。A在V上的一个表示是一个代数同态A→End(V)。A在V上的所有的表示构成的空间RepV(A)是一个仿射概型。用函子的语言,这一问题表述如下:
记Alg 为所有带幺元的结合k−代数所构成的范畴,CommAlg 为其中的交换结合代数所构成的子范畴。考虑下列函子
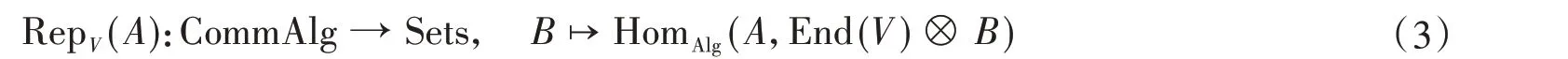
其中Sets是所有集合构成的范畴。
命题1RepV(A)是可表的,也就是说,存在一个交换代数AV,使得对任意的B,总有

该命题的证明可见参考文献[11]的§4.1。我们称由AV定义的概型为A在V上的表示概型(represen⁃tation scheme),自然地记为RepV(A),因此AV又可以写成k[RepV(A)]。
在RepV(A)上,存在一个自然的GL(V)作用:
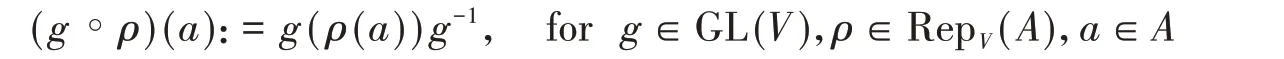
我们记RepV(A)GL(V)为对应的约化RepV(A)//GL(V)。事实上,RepV(A)GL(V)表示A在V上的所有表示的同构类。在文献中,如果V=kn,则RepV(A)和RepV(A)GL(V)分别记为Repn(A)和Repn(A)GL(n)。
一般地,RepV(A)和RepV(A)GL(V)都不是光滑的。为此,我们先回顾一个定义:
定义6(Cuntz−Quillen[13])如果一个有限生成的结合代数A满足下列等价条件:
(i)给定任意的k代数R及其幂零双边理想N,任意的同态φ∈HomAlgk(A,R N),总可以提升为一个同态-φ∈HomAlgk(A,R)使得φ是和自然投影R→R N是交换的;
(ii)对任意的A双模M,二阶Hochschild上同调HH2(A;M) = 0;
(iii)记乘法μ:A⊗A→A的核为Ω1(A),则Ω1(A)是A的投影双模,
那么我们称A是“形式光滑”的(formally smooth)或“准自由”的(quasi−free)。
例1下列代数是形式光滑的:
(i)由n个变量生成的自由结合代数k x1,x2,…,xn;
(ii)Matn(k);
(iii)k[X],这里X是一个光滑仿射曲线;
(iv)箭图生成的路径代数。
Ardizzoni,Galluzzi和Vaccarino在文[12]中给出了RepV(A)光滑的一个充分条件:
定理5([12],Theorems 4.6−4.7)若A是有限生成的形式光滑的k代数,则RepV(A)总是光滑的。
注意到形式光滑仅仅是一个代数的表示概型式光滑的充分条件,而非必要条件。一个例子是半单李代数的万有包络代数不是形式光滑的,但其表示概型式光滑的。文[12]给出了表示概型光滑的充要条件,即:
定理6([12],Theorem 3.3)设f:k[RepV(A)]→k是RepV(A)的一个点。则f是RepV(A)的一个正则点当且仅当对应的二阶Harrison上同调
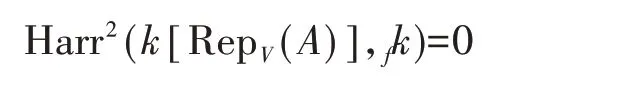
其中fk表示对应的k[RepV(A)]−模k。
在上述定理中,交换代数的Harrison 上同调是平行于结合代数的Hochschild 上同调的一个同调理论,具体见Harrison 的论文[14]。换句话说,对于一个代数A,其表示概型RepV(A)光滑与否存在障碍,而通常情况下,这个障碍不是平凡的。
3.2 Van den Bergh函子
弄清楚表示概型之后,接下来的一个问题是:如何把A上的结构关联到RepV(A)上?Van den Bergh 在文[15]中给出了一个构造,具体如下:设M是一个A−双模,则
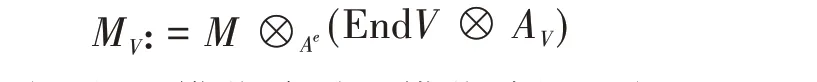
是一个AV−模。这样,我们就得到了从A的双模范畴到AV模范畴的一个函子

注意到交换代数的模范畴与其对应的仿射概型上的拟凝聚层范畴是等价的,Van den Bergh 的函子实际上也给出了从A的双模范畴到其表示概型的拟凝聚层范畴的一个函子。
在这个函子下,我们可以将A上的非交换切向量、非交换微分形式等(见§2.3)关联到其表示概型上的切向量场、微分形式等等。作为推论,我们重复定理3和定理4:
定理7[3−4]设A是一个结合代数,V是任意的一个线性空间。我们有:
(i)设{{−,−}}是A上的双泊松结构,则RepV(A)上存在一个泊松结构;
(ii)设ω∈DR2A是A上的双辛结构,则RepV(A)上存在一个辛结构。
至此,我们在Kontsevich−Rosenberg 原理的指导下,介绍了非交换泊松结构和非交换辛结构的构造。这是非交换几何的重要结果之一。当然,正如我们前面的所说的,除了箭图的例子之外,我们实际上是很难找到更多的例子了。注意到箭图的路径代数实际上是一个自由代数,同时注意到任何代数都存在一个自由的预解,那么我们有十足的动机作如下的考虑:我们是否可以在同伦的意义下考虑表示概型,并且在同伦的意义下考虑非交换的泊松结构和辛结构?这是我们下面要讨论的内容。
4 导出表示概型
在本小节,我们介绍Berest等引进的导出表示概型的概念,讨论它们的切空间、余切空间等性质。
首先注意到:设A是一个结合代数,固定线性空间V,则A在V上的表示概型给出了一个函子
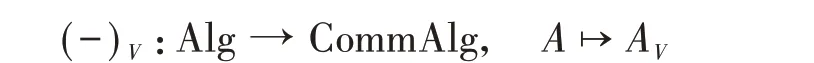
我们称该函子为V上的表示函子。事实上,表示函子可以扩展到微分分次代数上:对于任意给定的一个微分分次向量空间V,存在着一个函子
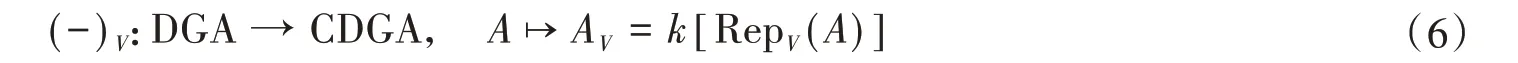
使得
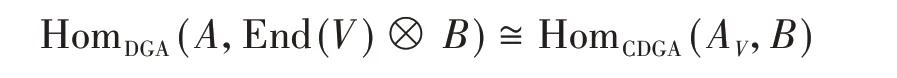
根据前面提到的Quillen的有理同伦论,DGA和CDGA 这两个范畴都具有“模型范畴结构”,因此都存在相应的同伦范畴,即这两个范畴在拟同构下的局部化,记为Ho(DGA)和Ho(CDGA)。这两个范畴中的对象,都存在着“准自由”的逼近(见§3),也就是说对任意一对象(A,d),其中d是微分,存在代数的拟同构
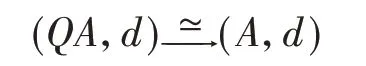
并且QA是准自由的,这些QA称为余纤维化分解(cofibrant resolution)。对于函子(6),可以证明,它能够提升到相应的同伦范畴上。这就是Berest,Khachatryan 和Ramadoss 在文献[5]中证明的一个重要的结果:

为“导出表示函子”(derived representation functor),并称DRepV(A)为A在V上的“导出表示概型”(de⁃rived representation scheme),称其同调H.(DRepV(A))为A在V上的“表示同调”(representation homology)。
对结合代数导出表示概型的研究揭示了该代数很多隐秘的信息,比如循环同调群、Hochschild 同调群以及Hochschild 上同调群等等,都自然而然地出现了。接下来,我们介绍导出表示概型的“函数空间”、“切空间”和“余切空间”,并将它们与上述概念联系起来。
4.1 导出迹映射和循环同调
回忆§2.1中,对任意的代数A∈Alg,任意的向量空间V,存在着一个迹映射
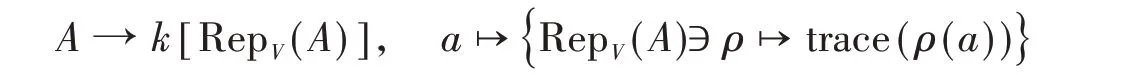
注意到这个迹映射通过(factor through)A♮:=A[A,A],并且像总是GL(V)不变的,因此一般把这个迹映射写成
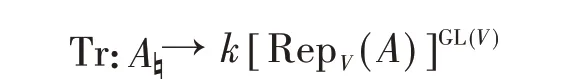
我们也称A♮为A上的函数,即迹映射把函数映到函数。
参考文献[5]的另一个重要结论说迹映射存在着一个导出版本。为了说明该结论,我们首先回忆一下结合代数的循环复形(cyclic complex)的概念。代数A的循环复形CC.(A)是下图中1 −T的余核构成的复形(这部分内容可以参考Loday的书[16]):

其中
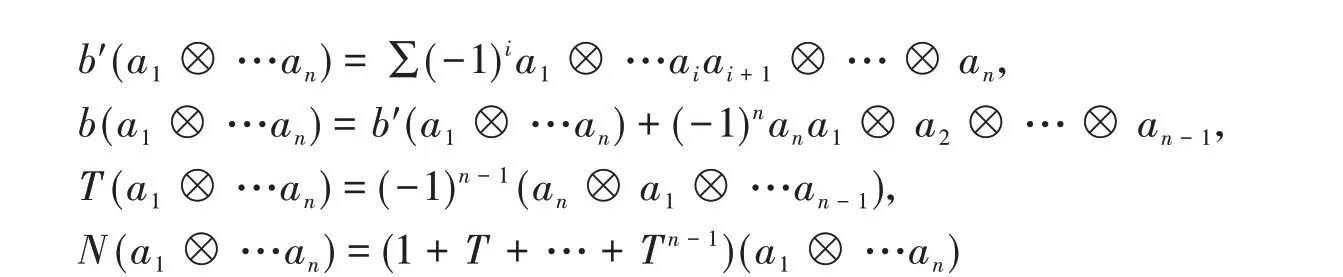
其同调群称为A的循环同调群,记为HC.(A)。在上图中,b−复形称为A的Hochschild 链复形,记为CH.(A),其同调群称为A的Hochschild 同调群,记为HH.(A)。若代数A是增广的(augmented),则我们有如下分解

参考文献[5]的Proposition 4.2 给出了该结论一个新的范畴化的证明。因为CC.(A) →----CC .(A)是分裂的,满的,且R♮=Rˉ♮+k,所以存在一个满映射
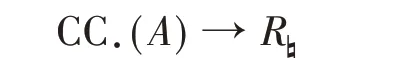
结合式(7)~(9),我们可以得到如下结论:
定理9([5]Proposition 4.1)设A是一个微分分次代数,则存在一个自然映射,称为“导出迹映射”(derived trace map)

使得该映射的像生成的函数在每一个分次上(degree−wise)是满的。
换句话说,对于一个结合代数A,它的“导出函数”是其循环链复形,并且在导出意义下,我们有迹映射把导出的函数映到其导出表示概型上的函数。
4.2 切向量场与余切向量场
类似地,我们可以考虑导出意义下的“非交换切向量场”和“余切向量场”。这些概念完全平行于§2.3,因此我们只是简略地提一下,具体内容请参考文献[5−6,18,20]。
设结合代数A的一个余纤维化分解为QA,我们称Der(QA,QA⊗QA)和Ω1(QA)为A的导出意义下的“非交换切向量场”和“非交换余切向量场”;在Van den Bergh 函子下,它们分别映到A的导出表示概型DRepn(A)上的切向量场和余切向量场。
此 外, Ω1(QA) 和Der(QA,QA⊗QA), 作 为QA双 模, 对 应 的 交 换 子 商 空 间, Ω1(QA)♮和Der(QA,QA⊗QA)♮分别对应于A的Hochschild 链复形CH.(A)和上链复形CH.(A),从而我们有导出的迹映射:
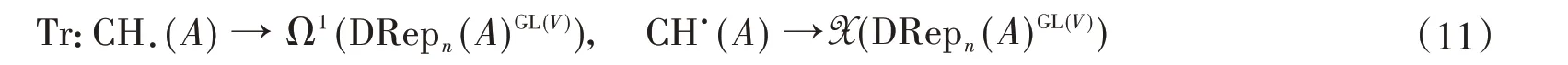
其中Ω1(−)和X(−)分别表示相应空间上的微分1−形式(余切向量场)和切向量场。
4.3 导出非交换泊松结构和辛结构
有了上述这些背景,我们介绍导出的非交换泊松结构和非交换辛结构就非常容易了。
定义8[18](导出非交换泊松结构)设A是微分分次代数。一个A上的度数为n的“导出非交换泊松结构”(derived non−commutative Poisson structure)是A的一个余纤维化预解QA上的度数为n的微分分次H0−泊松结构,即(QA)♮是一个度数为n的微分分次李代数使得对任意的-a∈(QA)♮
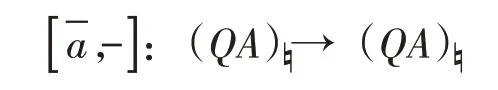
总是由代数QA的一个与微分交换的导子da:QA→QA诱导而来的。
在文献上,度数为n的泊松结构,也称为n−次“平移泊松结构”(见Calaque 等的论文[19])。导出非交换Poisson括号在同伦意义下是不依赖于分解QA的选择的,因此在微分分次代数的同伦范畴上是良定义的。下列结果为文献[18]所证明:
定理10([18]Theorem 2)设A是微分分次代数,且具有一个度数为n的导出非交换泊松结构。则对任意的向量空间V,A的导出同调H.(DRepV(A)GL(V))上存在唯一的度数为n的分次泊松代数结构使得导出迹映射是一个分次李代数同态。
当然,我们也可以讨论导出意义下Van den Bergh 的双泊松结构以及DRepV(A)上的泊松结构,在此不再赘述。类似地,我们有:
定义9[21](导出非交换辛结构)设A是微分分次代数。A上的度数为n的“导出非交换n−次平移辛结构”(derived non−commutativen−shifted symplectic structure)是A的一个余纤维化预解QA上的度数为n的闭的、非退化的(2 −n)−形式ω∈DR2(QA)。
在这里,注意到DR.(QA)实际上有两个微分,一个是de Rham 微分,一个是从QA上遗传来的微分,因此“闭”在这里的意思是:在DR.(QA)对应的负循环链复形(negative cyclic complex)中是闭的。我们有如下定理:
定理11([21]Theorem 5.7)设A是微分分次代数,且具有一个导出非交换n−次平移辛结构。则对任意的向量空间V,DRepV(A)上存在n−次平移辛结构。
在这个定理中,平移辛结构的概念是Pantev等在文[22]中首次提出的;定义9中给出的可以看成是该概念的非交换版本。前面提到的文献[19]是该论文的后续。
注记3在本小节,我们实际上模糊处理了DRepV(A)和DRepV(A)GL(V)的区别。在介绍非交换泊松结构的时候,因为Van den Bergh 的双泊松结构自然给出了Crawley−Boevey 的H0−泊松结构,所以前者不仅给出了DRepV(A)上的泊松结构,也给出了DRepV(A)GL(V)上的泊松结构。在研究非交换辛结构的时候,DRepV(A)和DRepV(A)GL(V)上的切向量场与余切向量场是有区别的,因此前者上的辛结构并不能给出后者上的辛结构,反之亦是如此。尽管如此,通过对非交换的切向量场和余切向量场的定义稍加改动(具体讨论可见文[21,23],并参见定理16),我们可以分别得到DRepV(A)GL(V)上的辛结构。为了得到DRepV(A)GL(V)上的辛结构的例子,我们接下来讨论卡拉比−丘代数。
5 卡拉比−丘代数
2007年,Ginzburg在arXiv论文预印本网站发表了论文[24]。在文中,他首次引入了“卡拉比−丘代数”的概念。这一概念不仅总结了前人(例如Kontsevich 等)在此领域的结果,而且开辟了很多新的研究方向,引起了很多数学家的关注与研究。
定义10(Ginzburg)假设A是一个特征为0 的数域k上的结合代数。我们称A是一个n维的“卡拉比−丘代数”,如果它满足以下两个条件:
(i)A是同调光滑的(homologically smooth),也就是说,作为Ae−模,A存在一个有限长度的、并且是有限生成的投射预解;
(ii)作为Ae−模范畴的导出范畴中的对象,存在同构

注记4(i)在上述定义中,如果A是交换的,则:条件(i)等价于说,A对应的仿射概型,也即素谱SpecA是光滑的(这是Serre 的一个结果);条件(ii)等价于说,SpecA的典则层(canonical sheaf)是平凡的。由此,我们得到:对于一个交换代数A,它是一个卡拉比−丘代数当且仅当SpecA是一个卡拉比−丘概型。对于同构(12),Van den Bergh后来证明:在相差一个内自同构的意义下,该同构是唯一的。
(ii)卡拉比−丘代数与文献中的Artin−Schelter 正则代数关系非常密切。实际上,如果我们在同构(12)中,只要求同构既是左A−模同构,又是右A−模同构,但是不一定是双模同构,则在此情形下,该代数就是一个Artin−Schelter 正则代数。换句话说,卡拉比−丘代数是Artin−Schelter 正则代数的特殊情形,反过来,Artin−Schelter 正则代数也称为“扭曲”的(twisted)卡拉比−丘代数(具体内容见Reyes 等的论文[25])。
下面我们给出卡拉比−丘代数的几个例子(以下代数有时候不限定基域是k)。
例2(包络代数)假设g 是一个有限维的李代数。我们称g 是幺模的(unimodular),如果任意a∈g 的共轭作用

并且称ℂ[x,y,z]⋊Γ)为ℂ3/Γ 的“非交换无差异消解”(noncommutative crepant resolution,简称NCCR)。在一般情况下,一个奇点的非交换无差异消解,如果存在的话,都是卡拉比−丘代数。
例4(Ginzburg代数)Ginzburg在文[24]中用箭图构造了一类微分分次代数(现在人们称为Ginzburg代数),并猜测:这类代数是卡拉比−丘代数。这一猜测后来被Keller和Van den Bergh证明(见文[28])。
Broomhead 证明,任意一个3−维仿射、Gorenstein 孤立奇点,都存在非交换的无差异消解;该无差异消解是一个3维Ginzburg代数[29]。
例5(基本群的群代数)一个流形M称为“无球”(aspherical)的,如果它的万有复叠空间是可缩的。对于一个无球闭流形,它的基本群的群代数是一个卡拉比−丘代数。在文[24]中,Ginzburg曾经猜测,3维无球闭流形的基本群的群代数,作为一个卡拉比−丘代数,是由一个非交换势函数给出的Jacobi 代数。这一猜测后来被Davison否定[30]。
5.1 从卡拉比−丘代数到卡拉比−丘范畴
在1990年代初,日本数学家Fukaya(深谷贤治)在研究辛流形上相交型Floer同调群的时候,发现了辛流形的Lagrange子流形组成一个特殊的结构,他称之为A∞范畴。简单地说,一个A∞范畴不是一个范畴,而是在相差一个“同伦”的意义下形成一个范畴,而这些同伦之间又存在同伦,以及同伦的同伦等等,一直至于无穷。这一结构,现在称为Fukaya范畴,可以说是Stasheff在1960年代发现的流形的闭路空间上的A∞结构的范畴化版本。
在1994 年的世界数学家大会上,在数学界崭露头角的Kontsevich 提出了著名的“同调镜像对称猜测”(Homological Mirror Symmetry Conjecture)指出:对于一个卡拉比−丘流形,存在另一个卡拉比−丘流形,称为前者的“镜像”,使得前者的Fukaya范畴与后者的凝聚层范畴导出等价,前者的凝聚层范畴与后者的Fukaya范畴导出等价(见文[31])。同调镜像对称猜测可以说是近二十多年来数学物理领域最重要的猜测,获得了人们广泛的研究,并取得了丰硕的成果。
Kontsevich 还指出,这两个范畴都是一类“非交换的辛空间”,后来Costello[32]等称之为卡拉比−丘范畴,并且证明一个卡拉比−丘范畴等价于一个“开”的拓扑共形场论(topological conformal field theory,简称TCFT)。下面,我们对这一重要概念稍微详细地加以介绍(更详细的内容可见文[32])。
定义11(A∞范畴)一个A∞范畴A是由对象集合Ob(A),及对任意的对象A1,A2∈Ob(A)对应的k上的分次线性空间Hom(A1,A2)构成的,并且对所有n= 1,2,…,都存在着度数为|mn|= 2 −n的多重线性映射:

在文献中,有时候也把上述范畴的同伦范畴称为卡拉比−丘范畴而不加以区分;在文[33]中,作者们也称之为非交换的卡拉比−丘空间。
例6(凝聚层范畴)设X是一个d维卡拉比−丘流形,则X上的有界凝聚层范畴D(X)是一个d维的卡拉比−丘范畴。
在本例中,m1是相应的态射空间上的微分,m2是态射的复合,而m3及后面的mn都是0;相应的配对则由Serre对偶给出。具体证明可以参见Huybrechts[34]的书第三章。
例7(Fukaya范畴)设M是一个辛流形。直观地说,辛流形M的Fukaya范畴Fuk(M)定义如下:其对象为M中的Lagrange 子流形,对任意两个横截相交的对象L1和L2,其态射空间Hom(L1,L2)定义为对应的Floer 上链复形,即由所有L1和L2的横截相交点张成的空间,并且对任意的n+ 1 个Lagrange 子流形L1,…,Ln+1,多重线性映射
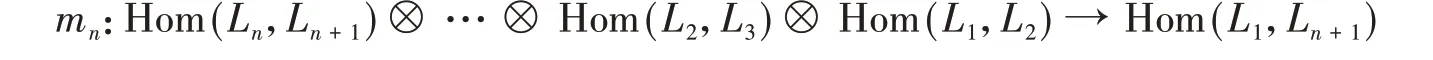
的定义是通过计数边界落在L1,…,Ln+1的拟全纯圆盘的个数而得到。Fukaya和Seidel等证明:如果M的条件充分好(例如第一陈类为0),则Fuk(M)是一个卡拉比−丘范畴,其中的配对由流形的Poincaré 对偶给出。
这一结论中A∞范畴结构(13)的证明,可以参考Fukaya等[35]的专著以及Seidel[36]的专著,而其中非退化配对(14)的存在性在Seidel的书中亦有证明。后来Fukaya告诉本文作者,对于一般的辛流形,这一结论也是成立的。
关于卡拉比−丘代数和卡拉比−丘范畴的关系,我们有如下定理(其证明见文[37]):
定理12设A是一个卡拉比−丘代数,则A的有限维微分分次模组成的范畴的导出范畴是一个卡拉比−丘范畴。
因为这个密切的关系,有些文献中也把满足定义10 中两个条件的范畴称为卡拉比−丘范畴(例如文献[38])。
5.2 卡拉比−丘范畴与非交换几何
如前所述,Kontsevich 等认为(具体可见文[31,33]),卡拉比−丘范畴实际上等价于非交换的辛空间。直到现在,人们还在发掘这一论断背后的几何意义。例如,Pantev等证明:
定理13([22]Theorem 0.1)设X是一个卡拉比−丘射影流形。则X上的凝聚层的导出范畴的模空间上存在一个平移辛结构。
关于Fukaya范畴上的非交换几何理论,这方面的研究近年来有增多的趋势。前面提到的Seidel及其学生Abouzaid、Sheridan,以及Lekili等都做出很重要的工作。对于其中的非交换Poisson结构,试举一例:
定理14([39]Theorem 17) 设M是一个2d维的恰当辛流形且满足c1(M) = 0。则M的Fukaya 范畴Fuk(M)上具有一个度数为2−d的微分分次双泊松结构。
6 卡拉比−丘代数的导出表示概型
在本小节,我们讨论卡拉比−丘代数的导出表示概型,并讨论其上的非交换泊松结构和辛结构。为了表述的方便,我们假设这些代数都是Koszul的。事实上,我们遇到的大部分卡拉比−丘代数都是(某种意义下)Koszul的。
6.1 Koszul对偶

6.2 非交换泊松结构和辛结构
下面我们考虑Koszul 的卡拉比−丘代数。这类代数有一个非常好的性质,这是由Van den Bergh 给出的:
定理17([41]Theorem 11.1)设A是一个Koszul 代数,则A是一个n维卡拉比−丘代数当且仅当它的Koszul对偶A!是一个对称的Frobenius代数,即存在A!−双模同构

根据双辛结构的定义,结合定理16和定理17,我们立即得到:
定理18[21,23]设A是一个Koszul的n维卡拉比−丘代数。则A上存在一个导出意义下的非交换的双辛结构,该双辛结构诱导了DRepV(A)GL(V)上的(2 −n)次平移辛结构。
回忆§2.4中关于非交换辛结构与非交换泊松结构的关系,定理18有如下推论:
推论1[18,20,42,44]设A是一个Koszul 的n维卡拉比−丘代数。则A上存在一个导出意义下的非交换的双泊松结构,该双泊松结构诱导了DRepV(A)GL(V)上的(2 −n)次平移泊松结构。
6.3 应用
通过学习非交换泊松结构,我们得到了结合代数的一些以前不知道的结构。在本文的最后,我们讲述几个这样的例子。
首先回忆在微分几何中,设(M,π)是一个泊松流形,则M上的微分形式空间Ω1(M)是泊松代数C∞(M)的一个李模:
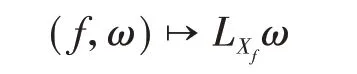
其中f∈C∞(M),ω∈Ω1(M),Xf是函数f的汉密尔顿向量场。同时,de Rham 微分
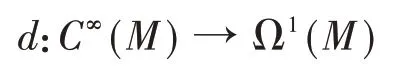
是泊松代数C∞(M)的李模同态。
在导出泊松几何中,我们也有类似的结论。回忆前面§4.1~4.2所述,代数A的循环同调HC.(A)可以认为是A的导出意义下的函数,而A的Hochschild同调HH.+1(A)与A的导出意义下的微分1−形式关系密切(见式(11)),Connes循环算子B则类似于de Rham微分。本文部分作者和杨松在文[20]中证明:
定理19([20]Theorems 1.1−1.2)设A是一个n维的Koszul 卡拉比−丘代数。则:
(i)A上存在着一个度数为2 −n的导出泊松代数结构,且该导出泊松结构诱导了A的循环同调HC.(A)上的一个度数为2 −n的分次李代数结构;
(ii)HH.(A)上具有一个度数为2 −n的HC.(A)−李模结构,并且正合序列
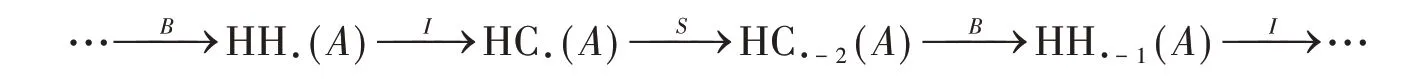
是度数为2 −n的HC.(A)的李模映射。
关于定理中长正合列的具体内容,请参考Loday的书[16]。在同一文章中,我们还给出如下论断,后来被Ramadoss和张忆宁证明:
定理20([44]Theorem 4.2)设A是一个n维的Koszul卡拉比−丘代数。我们有李模映射的交换图
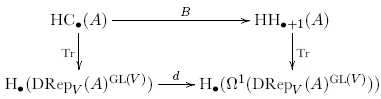
关于导出非交换泊松结构的其他应用,如在弦拓扑、表示论和导出代数几何等领域的应用,可参见文献[42−43]等。最后,我们提两个有趣的问题,与大家一起探讨:
问题1 在§1.5小节,我们将卡拉比−丘流形上凝聚层范畴的Serre对偶定理解释成其模空间上的平移辛结构。对于一般的n维射影流形,我们仍然有Serre对偶定理
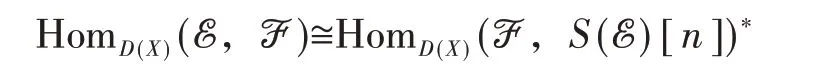
其中S是Serre函子。我们的问题是:这个一般情形的定理给出了流形凝聚层范畴的模空间上的什么结构?
问题2 在本文中,我们主要考虑了结合代数在线性空间上的表示及其导出情形。在代数几何中,我们还可以考虑代数簇的Hilbert 概型和Quot 概型,这些函子也都存在导出的版本。一个自然的问题是:对于结合代数,是否存在导出的非交换Hilbert概型和Quot概型?如果存在,如何刻画它们?
致谢本文的撰写得到中山大学胡建勋教授的支持与鼓励,并得到杨松、杨向东的协助,作者们向以上诸位表示诚挚的谢意。
