基于ARFIMA模型的钢材价格预测研究
2020-10-20申建红徐文慧
陈 雪,申建红,2*,徐文慧,朱 琛
(1.青岛理工大学 管理工程学院,山东 青岛 266520;2.山东省高校智慧城市建设管理研究中心,山东 青岛 266520)
近年来,随着我国城镇化步伐的加快,建筑产业不断发展,工程承包企业之间的竞争日趋激烈。钢材作为工程建设的主要原材料,其价格直接影响着工程承包企业的成本和利润。科学合理地运用价格预测技术,准确把握钢材价格的变化趋势,是工程承包企业制定合理采购策略和库存优化的依据。
目前,国内外针对钢材价格的预测研究相对薄弱。陈海鹏等人综合考虑螺纹钢原材料结算价与货币汇率等因素对螺纹钢价格变动的影响,提出了一种基于岭估计法的线性回归预测模型,通过与未来螺纹钢的交易价格进行对比验证,得到该模型预测精度较高[1]。陈希等人针对钢材价格变动性较大的现象,利用Levenberg-Marquardt方法改进的BP神经网络建立了钢材价格预测模型,同时结合1990—2008年的数据对模型进行训练预测,结果显示所建立的钢材价格预测模型有较好的预测精准度[2]。胡六星为提高工程造价效率以钢材价格为研究对象,在提炼出其趋势项的基础上利用残差序列建立了自回归移动平均模型(Auto-Regressive Moving Average Model,ARMA),并应用该模型对钢材价格进行分析预测,同时结合真实价格进行精度验证,得到其预测结果误差低于5%[3]。王雪飞等人通过建立差分自回归移动平均模型(Autoregressive Integrated Moving Average model,ARIMA),对多种钢材价格进行预测分析,实验结果表明该模型的短期预测效果较好[4-5]。王松等人应用广义自回归条件异方差(GARCH)模型与ARMA模型相结合的组合模型对近十六年Myspic钢材价格的变动率进行实证分析,发现钢材价格的时间序列中含有着明显的长短记忆特征[6]。Kaijian He等人对初始时间序列进行空间重构,并采用曲线去噪方法分离和剔除噪声干扰,实现了对原始时间序列中的动态混沌数据特征进行建模。其所提出的模型在统计上比传统的标杆模型具有更强的鲁棒性[7]。Tsung-Yin Ou等人提出了一种极限学习机器(ELM)法与灰色关联分析(GRA)法相结合的材料价格组合预测模型,其预测能力优于ARIMA和GARCH模型,可以更准确、快速地预测原材料价格[8]。
目前关于钢材价格预测的研究只考虑了钢材价格变动的短记忆性,并未考虑其价格变动的长记忆性对预测结果的影响。为此,本文从螺纹钢价格时间序列出发,引入钢材价格变动的长记忆性指标,从而建立了基于分数差分自回归移动平均(Autoregressive fractionally integrated moving average,ARFIMA)模型的钢材价格预测模型,通过对钢材价格时间序列变动特性的分析并借助MATLAB软件编程进行了钢材价格的预测[9]。并利用ARFIMA模型和ARIMA模型的预测值与真实值进行对比分析,实验结果显示,ARFIMA模型的钢材价格预测精准度更高。
1 基本模型
1.1 ARMA及ARIMA模型
ARMA模型可认为由自回归模型(AR)和移动平均模型(MA)组成,通常可记为ARMA(p,q),其形式为:
Xt=φ0+φ1Xt-1+φ2Xt-2+…+φpXt-p+
εt-θ1εt-1-θ2εt-2-…-θqεt-q
(1)
式中:{εt}是白噪声序列,p为自回归模型阶数,q为移动平均模型阶数,φ1,φ2,…,φp和θ1,θ2,…,θq为参数,且φp≠0,θq≠0。
若使用后移算子B表示,ARMA模型可简写为:
Φ(B)Xt=Θ(B)εt
(2)
BXt=Xt-1
(3)
ARMA模型适合于分析平稳时间序列,即其均值不受时间影响且方差收敛的狭义平稳过程。目前,由于多数时间序列呈现出非平稳性,因此ARMA模型不再适用。而ARIMA模型则适用于分析非平稳时间序列,它是在ARMA模型的基础上加入差分处理,通过剔除时间序列中非平稳趋势,得到平稳时间序列,从而展开分析研究。其模型ARIMA(p,d,q)形式为:
φ(L)(1-L)dXt=θ(L)εt
(4)
式中:L为滞后算子,d为差分参数,{εt}是白噪声序列,φ(L)和θ(L)分别为p阶与q阶平稳的滞后算子,可表示为:
φ(L)=1-φ1L-φ2L2-…-φpLp
(5)
θ(L)=1-θ1L-θ2L2-…-θqLq
(6)
式中:p,d,q均为非负整数。
1.2 ARFIMA模型
在ARIMA模型中,当0 (7) 对于任何d>-1的实数,上式都可以用一个超几何函数表示为: (8) 式中:Γ(x)为Gamma函数。差分参数d可以通过赫斯指数(H)来确定[10],d=H-0.5。 对于一个由N个数值组成的时间序列集合Xt,将其划分成长度为n的m个子序列,并将这m个子序列的均值都定义为: (9) 式中:xk,l为第l个时间序列中第k个观测量。 计算每个子序列的累计均值离差为: (10) 根据上式,计算出每个子序列的极差为: (11) 则其重标极差均值可表示为: (12) 式中:Sl表示第l个子序列的标准差为: (13) 如果时间序列满足: (R/S)n=αnH (14) 则该时间序列符合赫斯特率,式中,α为系数,H为赫斯指数。其中H可以由公式(14)两侧取对数,并结合最小二乘法拟合得到。当0≤H<0.5时,则表示时间序列具有反持久性,其表现出强烈的异变特性;当H=0.5时,则表示时间序列为随机序列;当0.5 因此,ARFIMA模型能够避免过度差分,最大限度地保留时间序列在低频处的信息,更适用于具有长记忆性的时间序列分析研究。 本文在借助SPSS软件缺失值分析功能对钢材价格原始数据进行补齐的基础上,通过平稳性检验、长记忆性检验、数据拟合等过程利用ARFIMA模型对青岛市直径为18 mm的HRB400螺纹钢价格进行了分析预测,同时结合ARIMA模型对该钢材价格的预测结果进行对比分析。 本文数据选用青岛市2014年1月1日到2019年6月30日直径18 mm的HRB400钢材价格作为研究对象。共采集到样本数据1 875个,由于各种因素导致收集的原始数据存在部分缺失,共缺失131个。 为保证预测结果的准确性,本文采用SPSS软件缺失值分析功能对缺失数据进行了分析,并在此基础上将数据补齐。其中单变量统计结果见表1,通过SPSS数据分析中的多变异分析(MVA)得到钢材价格变动时间序列服从正态分布,且多变量检验(Little's MCAR)的显著性水平小于5%,由此可判断原始数据为随机缺失型数据。本文采用期望-最大似然估计法(EM)对存在缺失的原始数据进行填补。 表1 单变量统计 利用经数据处理后的钢材日价格共得到287个周价格样本作为初始时间序列,记为Xt。图1为利用SPSS软件对该时间段内青岛市直径为18 mm的HRB400螺纹钢价格数据绘制的时序图,其价格在早期呈现出下降趋势,后期呈现出上升趋势,初步识别为非平稳时间序列。并利用单位根检验-ADF方法检验时间序列Xt是否含有单位根。 图1 螺纹钢价格时序图 单位根检验结果如图2所示,初始时间序列Xt检验统计量大于各个临界值,此时原假设成立,即认为初始时间序列Xt是非平稳时间序列。 图2 时间序列Xt的ADF检验结果 图3为时间序列Xt的自相关函数图,图中表明钢材价格的变动没有明显的季节性变化,且自相关系数逐渐减小呈缓慢下降的趋势,在滞后80阶后才开始小于0,表现出长期相关特性,可初步判断时间序列Xt含有一定程度的长记忆性。根据公式(8)—公式(13)计算得到H为0.835,赫斯指数大于0.5进一步表明时间序列Xt确实具有较强的长记忆性。 图3 时间序列Xt自相关函数图 将样本数据分为两部分,取2014年1月1日到2019年5月12日的周价格数据,即前280个样本数据作为建模序列,记为Yt,用来构建ARFIMA模型和确定模型参数。取2019年5月13日至2019年6月30日的周价格数据,即后7个样本数据用来验证所建立的ARFIMA模型的可行性与精确度。 应用R/S分析法求得时间序列Yt的赫斯指数为0.835,则所建模型中的分数差分参数d为0.335。对时间序列Yt进行分数差分剔除其中存在的长记忆性,从而获得只含有短记忆的时间序列,记为Zt。图4为时间序列Zt的时序图,由图可知经分数差分后的时间序列Zt中的数据基本围绕基准线零线进行上下波动,并不存在显著的趋势或周期,此时可初步判断时间序列Zt已达到平稳。 图4 时间序列Zt时序图 采用ADF方法检验时间序列Zt是否还含有单位根,结果如图5所示,可以看出经过分数差分处理后的时间序列Zt检验统计量小于各个临界值,此时可判断该时间序列为平稳时间序列。通过利用混成检验(LB)法对该时间序列纯随机性进行检验,可知在前6阶和前12阶延迟下Q检验统计量的p值均小于0.05,于是时间序列Zt为纯随机序列的假设不成立,即认为时间序列Zt属于非白噪声序列。 图5 时间序列Zt的ADF检验结果 通过分数差分处理后的时间序列Zt的自相关系数在滞后2阶时其值小于2倍的标准差,同时偏自相关系数在滞后1阶时其值小于2倍的标准差,于是可以确定模型参数p=2,q=1。由此可建立模型为ARFIMA(2,0.335,1),并对时间序列Zt进行数据拟合,同时采用LB检验其残差序列,可知在前6阶和前12阶延迟下Q检验统计量的p值均大于0.05,此时认为该残差序列是白噪声序列,即可表明ARFIMA(2,0.335,1)是显著有效的。为了与ARIMA模型的预测结果进行对比分析,本文同时利用ARIMA模型对时间序列Yt进行数据处理,模型参数对比如表2所示。 表2 ARFIMA和ARIMA模型参数估计值 为了验证ARFIMA模型的适用性,根据以上模型参数估计,确定以ARFIMA(2,0.335,1)模型对直径为18 mm的HRB400钢材价格进行拟合预测。图6为ARFIMA(2,0.335,1)模型的拟合预测结果与真实值的比较,结果显示ARFIMA(2,0.335,1)具有很好的拟合效果。 本文通过分别利用ARIMA模型和ARFIMA模型对2019年5月13日至2019年6月30日,7周的钢材周价格进行预测分析,同时结合7周的真实值进行累计差值和相对误差的精度验证,如表3所示。从表中可以看出,ARIMA模型预测值较真实值的累计差值为777元,平均相对误差为2.08%;ARFIMA模型预测值较真实值的累计差值为175元,平均相对误差为0.38%。综上所述,在钢材价格预测中ARFIMA模型较ARIMA模型预测结果精度更高。 表3 ARFIMA模型和ARIMA模型预测结果 图6 ARFIMA(2,0.335,1)模型预测拟合图 本文以2014年1月~2019年6月青岛市直径18 mm的HRB400钢价格数据为样本,建立了ARFIMA(2,0.335,1)钢材价格预测模型,并与ARIMA模型进行对比分析,得出以下几点结论: 1)ARFIMA模型中的分数差分较ARIMA模型的整数差分能更好地保证钢材价格原始时间序列信息的完整性,避免有效信息的缺失。 2)螺纹钢价格时间序列具有较强的长记忆性,ARFIMA模型在保持ARIMA短期预测精度的基础上,充分考虑了钢材价格变动的长记忆性。 3)实验结果显示,ARFIMA模型预测值较真实值平均相对误差仅为0.38%,相较于ARIMA模型的钢材价格预测精准度提高了1.7%,且模型拟合度更高、预测效果更稳定。对于房地产企业及时掌握市场动向,降低库存资金占用率,制定短期钢材采购计划有一定的参考意义。2 基于ARFIMA模型的钢材价格预测
2.1 原始数据处理

2.2 ARFIMA模型
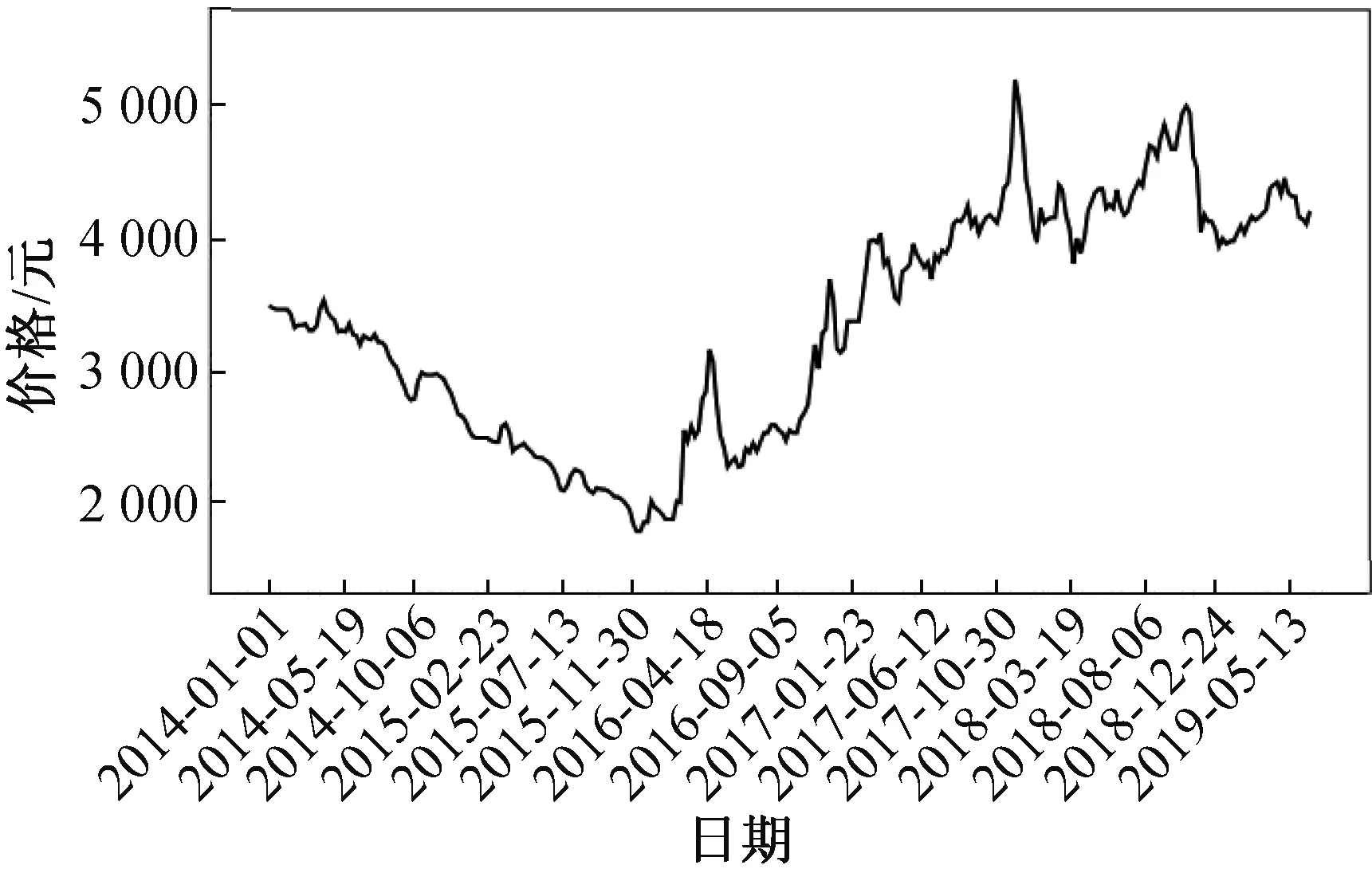

2.3 长记忆性检验

2.4 模型建立
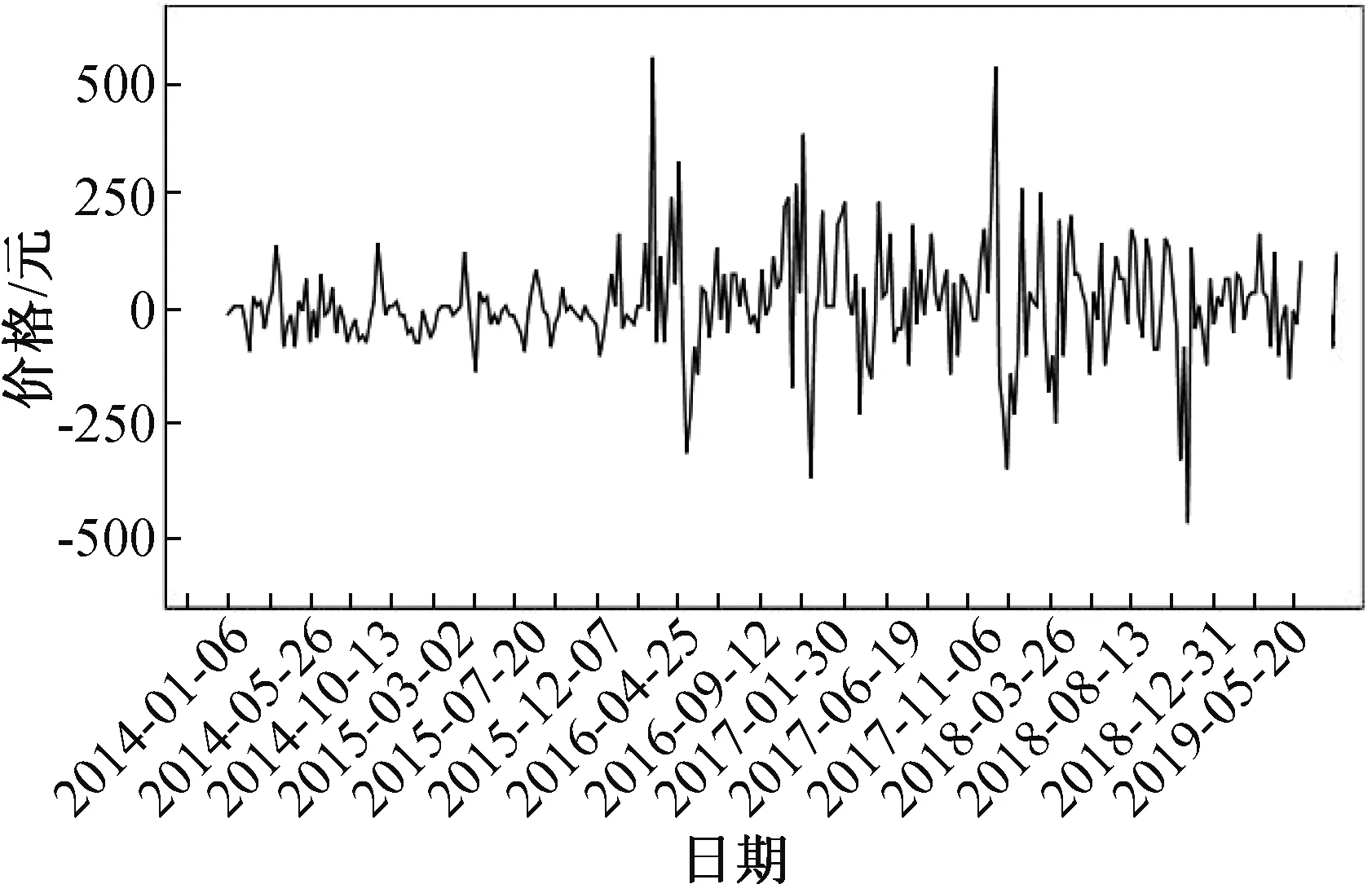


2.5 模型预测
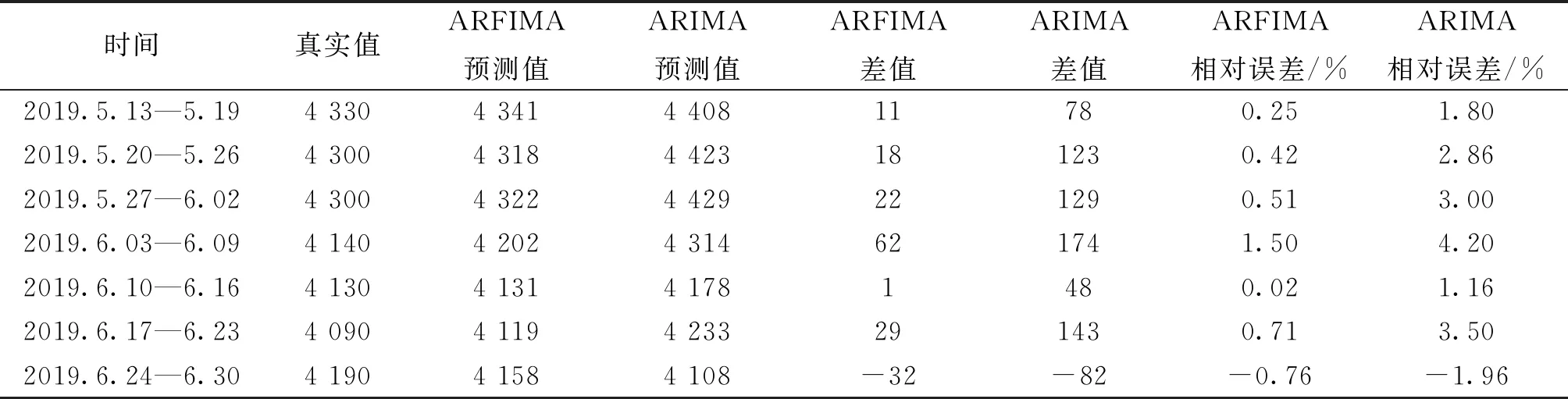
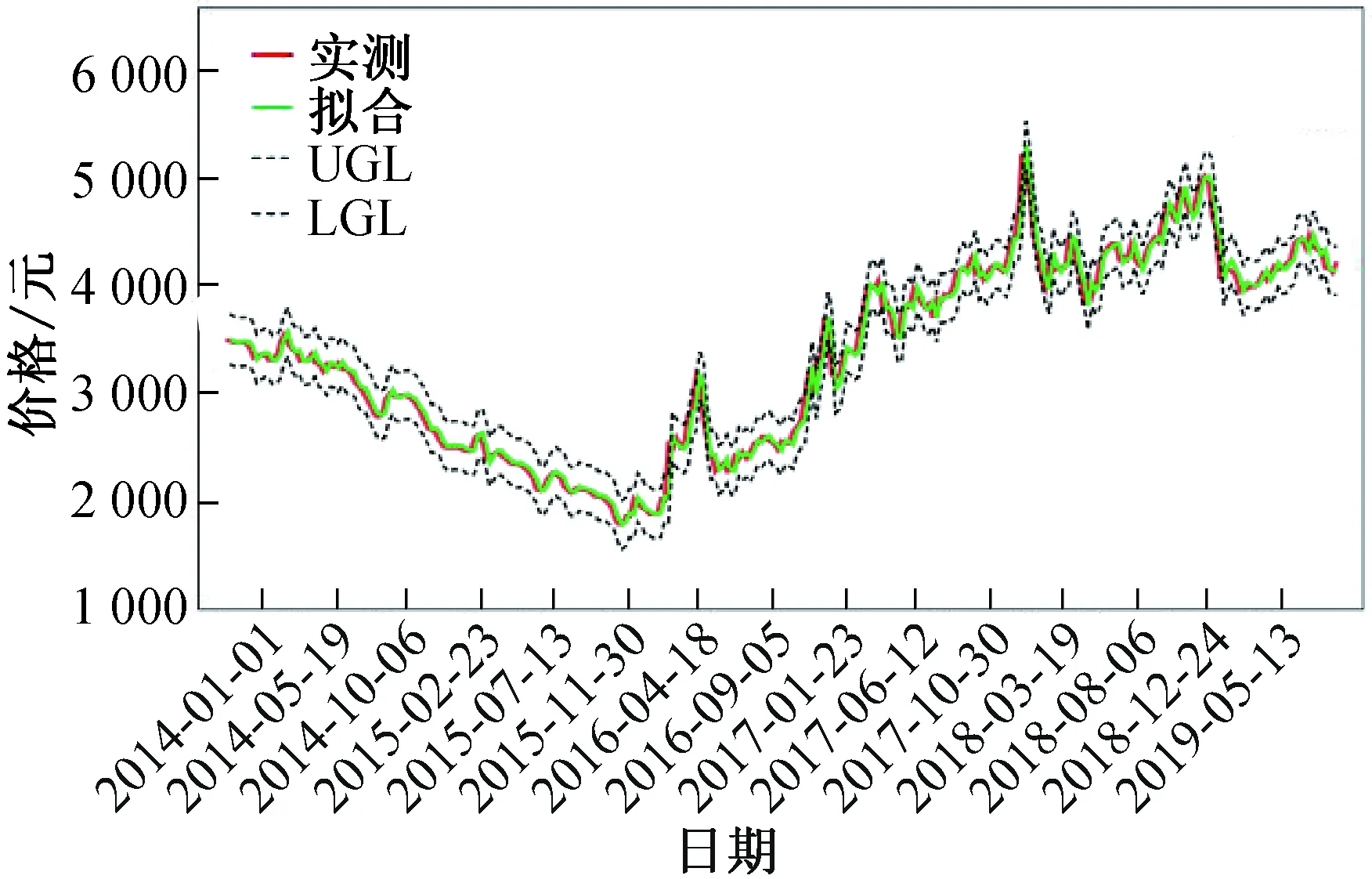
3 结论
