金沙江梯级水库群供水发电联合调度研究

2020-10-20陈雨菲董增川

河北工程大学学报(自然科学版) 2020年3期

陈雨菲，董增川

(河海大学水文水资源学院，江苏南京 211098)

水库的运行与管理需要满足多方面利益部门的用水需求，梯级水库群间存在复杂的水文、水力与电力联系[1]，过去的单目标水库优化调度难以满足新时期水库群优化调度的新需求。针对水库群发电供水目标联合优化调度，国内外研究学者从优化算法、模型求解和竞争协同关系等方面进行了深入研究[2-5]。一类学者采用约束法，将多目标问题转化为单目标问题，如徐斌[6]等选择梯级发电量最大作为优化目标，将防洪、供水目标转化为约束条件，揭示不同来水条件下目标间置换及协调关系。李想[7]等应用优化软件LINGO构建了供水与发电目标的水库调度模型，并采用非线性规划方法权衡了二者关系。Babel[8]等将生活、工业、生态等部门的需水满足程度转化为经济效益，再以各部门总经济效益最大为目标，建立了优化配置模型。上述学者虽然构建了水资源优化配置模型求解问题，但是无法得到供水发电两目标优化的非劣解集以进行多目标决策分析，难以对比出供水-发电目标在不同调度时期内的竞争关系，及不同偏好下调度方案的区别；同时其人为设置权重系数的主观性较大。另一类学者侧重于通过改进的智能优化算法求解多目标模型，如周华艳等[9]提出烟花量粒子群算法，在梯级联合优化调度中提高了总发电量。杨光等[10]引用基于CIS优选的决策因子，得到了分布更优的非劣解集。此类研究改进了模型求解难度与效率，但是却没有再对水库群多个目标间的具体关系进行联合分析，难以实现流域水资源联合调度下的效益最大化。金沙江梯级水库群作为我国水电资源开发的主要基地，由于其巨大的发电效益和流域的供水要求，对发电供水目标竞争协同机制研究具有重要意义，为实际调度决策提供支撑。本文建立了面向发电与供水目标的金沙江下游梯级电站多目标优化调度模型，引入置换率的概念对发电与供水目标进行具体量化分析，得到不同典型年下，不同时期内的供水与发电两目标间的竞争协同关系，以实现流域水资源效益最大化。

1 研究区域概况

金沙江是我国西南地区最大的江河之一，具有落差大，水能资源丰富等特点，在我国水力开发中占有极其重要的地位。其控制流域面积4.763×105km2，年平均流量4.75×103m3/s，降雨主要集中在6月—9月。金沙江下游已建和在建的向家坝、溪洛渡、白鹤滩、乌东德四座大型水利枢纽相连形成装机容量为44 670 MW的巨型梯级水库群[11]，水库工程特性见表1。基于流域自然地理特征和水量传输关系，对金沙江下游进行概化，见图1。对金沙江下游四库开展水库群联合优化调度研究，可以充分发挥梯级水库群的调蓄和补偿能力。

2 水库群优化调度模型

2.1 目标函数

(1)发电目标:梯级总发电量最大。

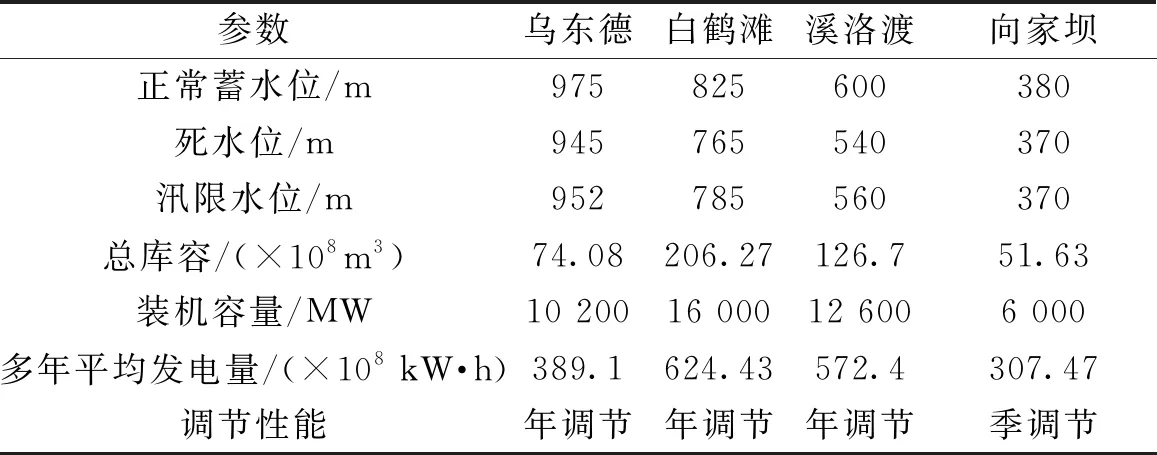
表1 水库工程特性表

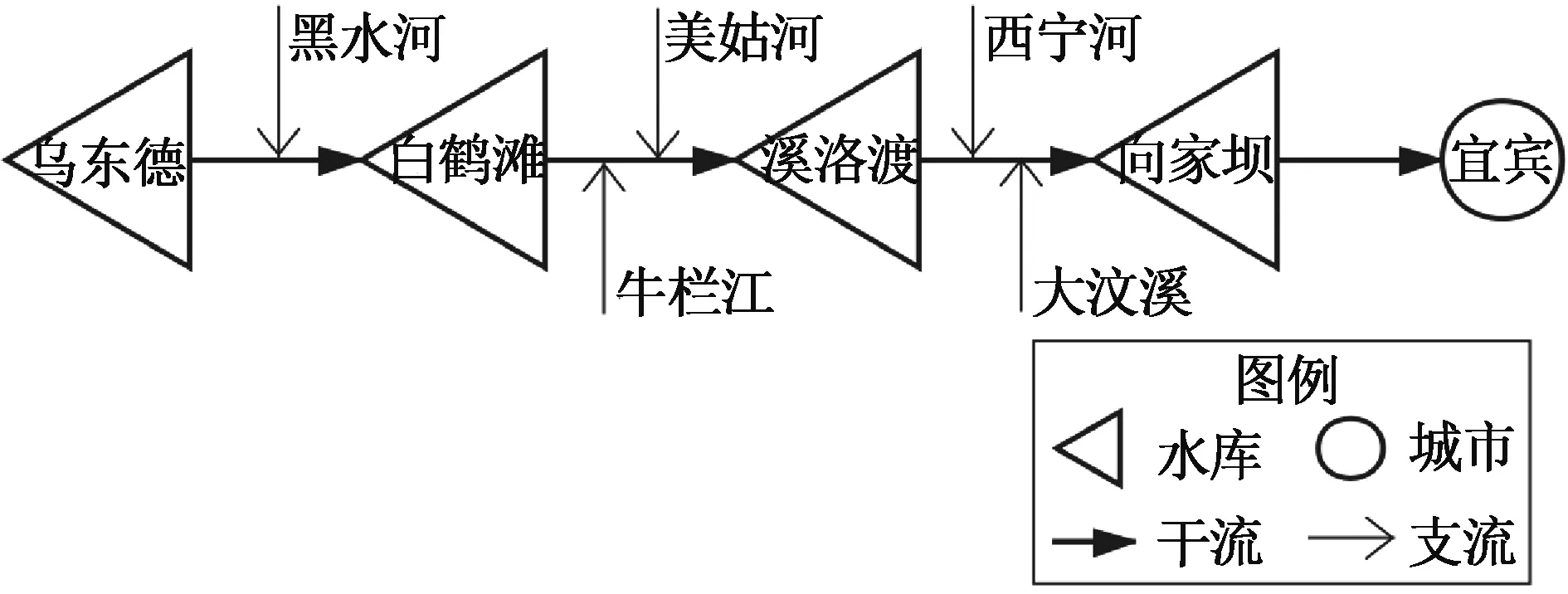
图1 金沙江下游流域概化图

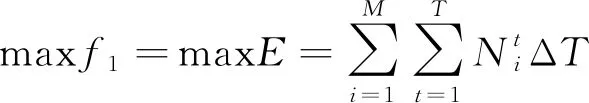
(1)

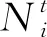
(2)供水目标：缺水量平方和最小。

(2)

式中：qt为梯级水库群在第t时段内的总供水量；Dt为流域在第t时段内的需水量。

2.2 约束条件

(1)水库水量平衡约束

Vi,t-Vi,t-1=(Ii,t-Qi,t)Δt

(3)

式中：Vi,t、Vi,t-1为i库第t时段末、初水库的库容，m3；Qi,t为i库第t时段平均出库流量，m3/s；Ii,t为i库第t时段内平均入库流量，m3/s；Δt为计算时段长。

(2)水库出流约束

Qi,t,min≤Qi,t≤Qi,t,max

(4)

式中：Qi,t,min为t时段i库最小出库流量，m3/s；Qi,t,max为t时段i库最大出库流量。

(3)水库水位约束

Zi,t,min≤Zi,t≤Zi,t,max

(5)

式中：Zi,t,min为t时段i库末最小允许水位，即为死水位，m；Zi,t,max为t时段i库末最大允许水位，在汛期为汛限水位，在非汛期为正常高水位[12]，m。

(4)出力约束

Ni,t,min≤Ni,t≤Ni,t,max

(6)

式中：Nit，min为i库t时段最小出力，万kW；Ni，t，max表示i库t时段最大出力，万kW。

(5)非负约束

Qi,t≥0

(7)

式中：Qi,t为i库第t时段出库流量。

2.3 模型求解

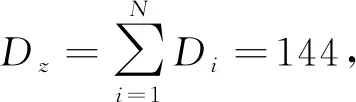
X=[Z1(1),Z1(2),…Z1(T+1),…

Zi(t),…,ZN(T+1)]

(8)

求解步骤如下：

(1)初始化模型参数，输入典型年下的金沙江下游四库在各时段的来水，在水位与流量约束范围内随机生成初始种群。

(2)计算水库下泄流量、出力等，利用罚函数淘汰不满足约束条件的种群个体。

(3)交叉与变异产生新的满足约束条件的子代种群，并将其与父代种群合并，依据目标函数值进行非支配排序，计算个体的拥挤度，从低到高进行挑选。

(4)采用精英策略保留优秀个体，即将父代也纳入到子代当中进行排序分析。

(5)重复上述步骤直至满足迭代次数，输出模型优化调度后的非劣解集。

3 模型结果分析

3.1 全周期发电供水目标关系分析

利用P-Ⅲ型分布曲线，对1957年至2015年金沙江下游水文站实测径流数据进行排频计算，选取1974年、1963年和1959年为典型年，分别对应于频率为25%、50%和75%的丰水年、平水年和枯水年。参照调度规则，选取本年度的11月上旬至次年的10月下旬为调度期，算法参数上将种群规模设为100，进化代数为500。求解模型可以得到三种典型年下，金沙江下游梯级水库电站多目标优化调度模型的非支配解集如图2所示。

缺水量平方和随着梯级发电量的增大，在不同典型年来水情况下都呈增长的趋势，即供水目标与发电目标呈竞争性。各典型年在一开始的增长趋势较为平缓，竞争关系较弱，当丰水年发电量超过2.19×1011kW·h，平水年发电量超过1.93×1011kW·h，枯水年发电量超过1.69×1011kW·h时，非劣解集出现拐点，斜率逐渐增大，增长趋势由缓变陡，竞争关系增强，单位发电量的增加将显著导致供水不足造成的供需矛盾。

对比不同典型年情况下的非劣解集可知，丰水年的发电量最大，缺水量平方和则为最小。平水年与枯水年在发电量较小时缺水量平方和数值相近，而随着发电量增加，平水年变化较小，枯水年的缺水量平方和显著增加，供需水矛盾最为突出，发电目标与供水目标竞争激烈。分析原因，主要由于在来水量丰沛时，供水效益得到满足，因而总缺水量较小，发电量较大，金沙江下游在丰水年来水较大，通过水库的调蓄作用可以基本满足需水要求，竞争关系较弱。

3.2 分周期下的发电供水目标竞争关系

为明确不同时段下发电与供水之间的竞争关系，基于Fisher最优分割法[16-17]，结合金沙江流域多年来水特征，将全年划分为蓄水期、供水期、汛前消落期以及汛期。(1)蓄水期：10月1日—10月31日。在该阶段内水库群的主要目标为供水，发电与蓄能。在电站出力不低于保证出力的前提下，尽快将水位从汛限水位蓄至正常高水位，以满足供水期金沙江下游片区的综合用水，提高水头的同时增加发电效益；(2)供水期：11月1日—次年6月10日。在该阶段内为满足下游生活需水，工业需水及农业需水，在天然径流来水较小时，由水库放水满足需水要求；(3)汛前消落期：6月11日—6月30日。在该阶段内雨量增大的同时径流增大，需尽快将水位降低至汛限水位，留出防洪库容，为汛期防洪应急做好准备；(4)汛期：7月1日—9月30日，在该阶段内由于金沙江流域水量丰沛，供水效益得到充分保障，仅考虑发电效益。在兴利调度的模型中，汛期时的水库水位根据防洪要求设定不超过汛限水位，下泄流量即来水流量。因此，将调度周期划分后，对非汛期的蓄水期、供水期及汛前消落期进行优化调度研究。由于枯水年来水较少，供需矛盾最为突出，竞争关系最强，选取其为典型年，以旬为调度时段，得到上述三个期内的非劣解前沿。

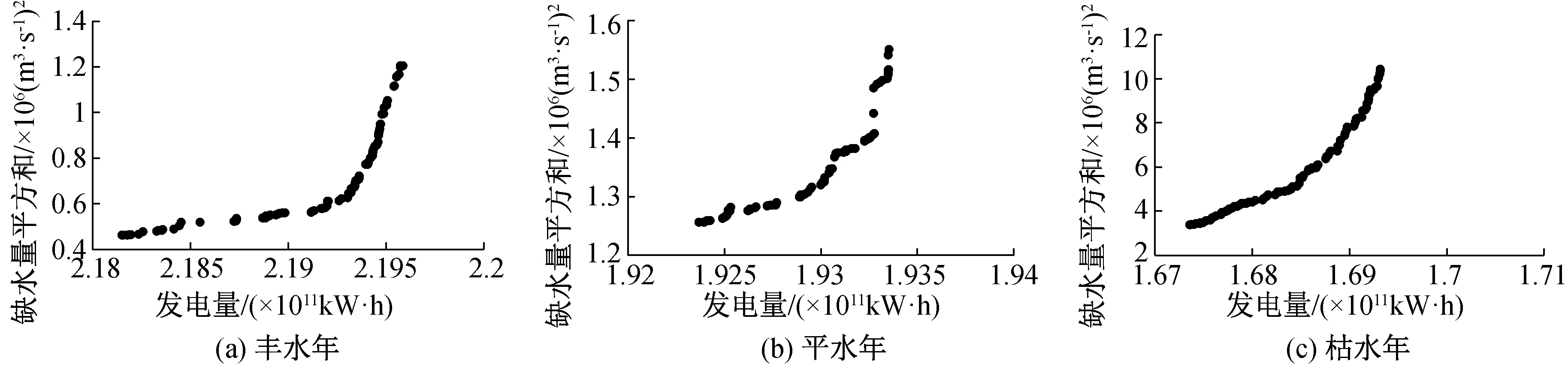
图2 不同典型年下的非劣解集

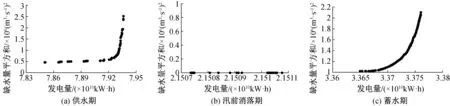
图3 分周期下的非劣解集

在供水期内，由于水库泄水，当发电量在7.92×1011kW·h内时，既能保证发电效益，又能在一定程度上满足下游需水，随着梯级发电量增加缺水量平方和较小且变化不大；若再提高梯级发电量，则需要减少水库下泄水量来抬高水库运行水位发电，可供水量减少，下游需水难以完全满足，导致缺水量平方和显著提高，竞争关系加强。在汛前消落期，由于金沙江流域来水丰沛，梯级水库群需要在一个月内将水位降低至汛限水位，可以满足金沙江下游需水，因此随着发电量增加，缺水量平方和始终为零，供水效益满足，供水与发电为协同关系。在蓄水期，当发电量小于3.37×1010kW·h时，缺水量平方和随着梯级发电量变化的趋势较缓。由于水库调度的主要目标是尽快蓄满，即水位尽快由汛限水位蓄至正常高水位，水库下泄流量减少，难以满足下游需水，增加单位发电量对供水效益产生很大影响，因此发电用水与流域供水间存在强竞争关系。

3.3 竞争协同关系量化分析

为进一步分析发电与供水的竞争机制，采用置换率[18]来表征两目标之间相互转化的指标，对于非劣前沿来说，目标间的偏置换率表示在局部非劣面上某点，在其他目标函数的值均固定不变的情况下，当第j个目标函数的值被提高(或降低)一个单位，必须由第i个目标函数的值降低(或提高)Tij个单位补偿，即通过目标的置换量反映目标间地影响的程度。目标函数yi=fi与yj=fj之间的非劣置换率定义如下:

(9)

式中：fi，fj为参与置换率分析的目标函数，λij为两目标函数之间的置换率。

利用软件1stOpt对枯水年供水期与蓄水期的发电供水竞争关系的非劣前沿进行函数拟合，得到梯级发电量与缺水量平方和的函数关系，求一阶导数后得到分周期下的置换率曲线见图4，选取三个差异较大的点形成偏供水方案、均衡方案和偏发电方案，定量度量单位目标的变化对另外目标的改变程度，与两目标间的变化关系见表2。

根据上述图表对比分析，在不同周期内的来水情况下，置换率与发电量呈正相关关系，提高发电效益的同时供水效益势必会受到影响。供水期发电量在7.931×1010kW·h内，置换率始终为零且增长较慢，水库供水与发电几乎不存在竞争关系，其后随着发电量增加，缺水量平方和显著增加，且变化幅度逐渐增大。蓄水期发电量在3.373×1010kW·h内，置换率曲线增长趋势较缓，而当梯级水库群为了追求高发电量时，在较短时间内抬高水库运行水位，单位发电量的增加将显著导致缺水量平方和的增加，容易引发供水区水资源供需矛盾，产生不利影响。枯水年相较于丰、平水年置换率始终较高，且随着梯级发电量增加，上升趋势更加明显。

图4 分周期下的置换率曲线

表2 枯水年典型方案置换率

不同周期内的不同偏好方案对梯级发电量影响较小，对缺水量平方和影响较大，若一味偏向发电目标最大化则对供水效益产生较大影响，难以实现下游水资源供需平衡。针对水库群在实际调度中的需求，可以合理选择水库的运行方式，在供水、发电的竞争博弈中选取偏好解。

3.4 典型非劣解方案调度过程分析

对枯水年水库调度过程进一步分析，在非劣解集中，挑选出偏供水方案、偏发电方案和均衡方案作为代表方案，其对应的水库运行水位过程如图5所示。三种方案在汛期前存在较大差异，偏供水方案为了保证下游供水充足，水库应该在可允许的范围内尽可能地向下游泄水，因此水位下降趋势最为明显。在接近汛期来水增大时，水库下泄水量满足下游需水的同时库容得到补充，水位提高，梯级发电量增加。偏发电方案为保证发电量最大，水库在较长时间内保持高水位，在大多数情况均在偏供水方案之上。均衡方案则介于二者之间，水位变化相对均匀，既要保证下游供水又维持适当水头保证发电效益。其中，向家坝水库由于是季调节水库，调节能力较弱，可调节库容小，水位变幅相对较大。