隧道开挖对邻近桩基影响的两阶段分析方法

张坤勇，徐 娜，臧振君，王乾坤，张彦红

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210024；2. 河海大学 岩土工程科学研究所，江苏 南京 210024；3. 江苏省宿迁市住建局，江苏 宿迁 223800；4. 上海市政工程设计研究总院(集团)有限公司，上海 200092；5.中铁(上海)投资集团有限公司，上海 200135)

随着新型城镇化进程的加快发展，对于充分规划利用好地下空间、发展好地下交通的需求越来越紧迫。并且城市地下空间巨大[1]，很多城市开始修建地铁。当城市的经济水平较高时，人口必然较多，建筑物也会很密集，这会给地铁的施工带来巨大的麻烦。因为在隧道开挖过程中，无论采用哪种施工方法，都不可避免地会对周围地层产生扰动，从而打破原有的平衡，出现地层位移[2]。当扰动较大时，建筑物桩基会出现较大的变形，当变形过大时，建筑物就会倒塌，造成工程事故的发生。因此，在实际工程中考虑隧道开挖对附近建筑物的影响越来越重要。

Mroueh和Shahrour[3-4]使用三维有限元软件建立整体模型，选用摩尔库伦土体本构模型，模拟隧道开挖对邻近桩基以及上部建筑物的影响。并比较在不同桩顶边界条件下桩身变形和内力的不同。张志强等[5]使用ANSYS来模拟深圳地铁盾构隧道施工过程对邻近地层的影响，该模型主要考虑隧道附近桩基础的存在对隧道开挖是否有遮拦效应。计算结果表明，当隧道开挖时，邻近建筑物桩基础会有靠近隧道方向的水平位移。所以需要提前做好监测和保护措施，以避免工程事故的发生。Lee和Jacobsz[6]使用有限元差分软件来分析隧道开挖对邻近桩基的影响，分析结果表明，隧道开挖引起桩基的水平位移要远大于竖向位移。数值模拟的准确性很大程度上取决于土体本构模型的选取以及材料参数的确定[7-9]，这样才可以得到较为准确的桩身附加响应。但该方法建模较为复杂，需要熟练使用建模软件，并且计算时间较长。所以该方法工程实用性较低。

本文基于Winkler地基模型[10]，该模型简单，并被广泛应用于地基工程，并且在解决实际问题的过程中积累了许多经验，被证明是有效的。然后采用两阶段分析方法[11]，建立隧道开挖条件下被动桩受力分析模型，推导出桩土相互作用控制方程。最后通过工程实例，验证本文计算方法合理可行，能够有效分析隧道开挖对邻近桩基的影响。

1 隧道开挖条件下被动桩受力分析

图1给出了隧道开挖条件下既有桩基的受力分析模型。该模型假设桩侧土体均匀且各向同性，桩身为线弹性本构模型，桩土之间变形协调。桩基在隧道开挖的作用下，桩侧桩土间相互作用力分别为p1和p2，简化模型如图1(a)所示，桩身两侧土体弹簧为并联形式，地基反力系数可改写为k=k1+k2，如图1(b)所示；桩基处的水平向土体自由位移场为q(z)，如图1(c)所示，然后将该自由场作为主动荷载作用于桩身，导致桩基的挠曲变形为y(z)，如图1(d)所示，因此桩土之间相互作用力可以写成下式：

(1)

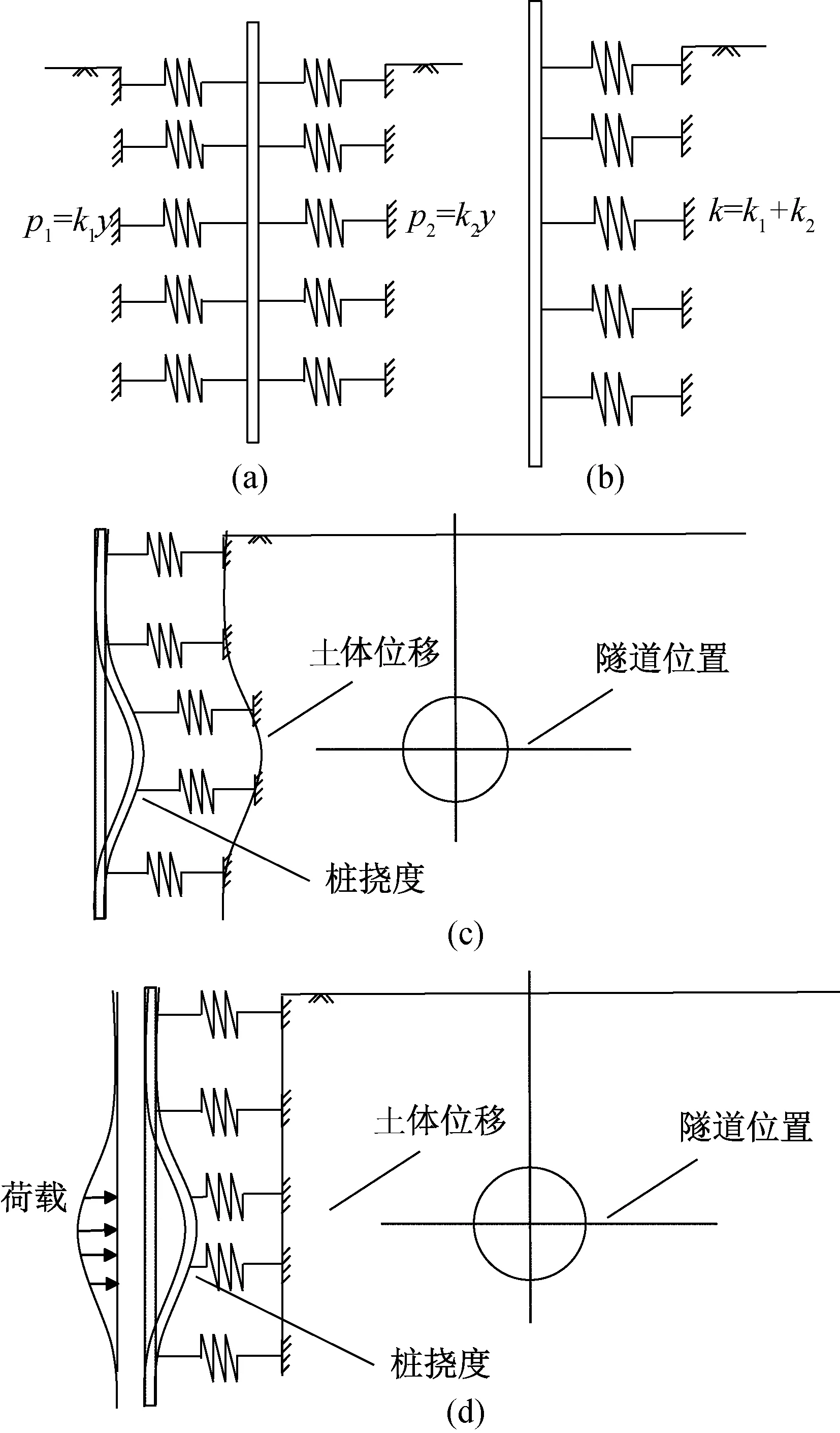
图1 隧道开挖下桩-土相互作用模型

2 桩土相互作用控制方程推导

工程实践中，既有桩基础一般均承受上部结构荷载，取桩身微单元建立受力分析模型如图2所示：

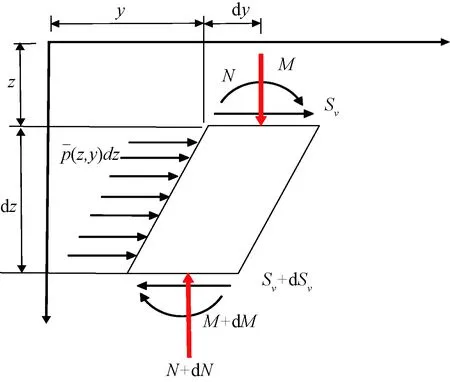
图2 桩单元受力分析

图2中，桩体单元的轴力作用点分别为桩单元上下截面的中心点，并且该桩体单元处于静力平衡状态。对该单元形心取矩可得：

(M+dM)-M+Ndy-Svdz=0

(2)

对式(2)化简得：

(3)

根据水平方向的合力为0可知：

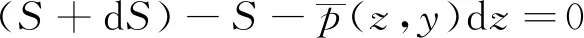
(4)

化简后得：

(5)

根据欧拉-伯努利梁理论得公式如下：

(6)

式中，E为桩体弹性模量；I为桩体截面惯性矩。

将式(5)和式(6)代入式(3)中，并对z再次求导，得：

(7)

(8)

式中，N(z)为桩的轴力沿桩长方向的函数，D为桩的宽度或半径。

将式(1)代入式(8)，得：

(9)

式(a)即为隧道开挖引起土体变形，从而桩身产生挠曲变形的桩土相互作用控制方程，该方程的求解是两阶段分析桩土相互作用的基础。

3 桩土相互作用控制方程求解

式(9)是四阶非齐次微分方程，不能直接求出该方程的解析解答。但该方程可以通过数值分析中有限差分法求得近似解。首先根据不同精度要求，将求解区域分成若干节点，然后对每个节点使用泰勒级数展开，即将高阶微分方程中的导数项消除建立差分格式；构造了差分格式后，对于前述高阶微分方程求解问题就转化为代数方程组问题，可编写成程序计算得到定解问题在离散单元上的离散解，进而应用插值法可以从离散解得到定解问题在整个定义域上的近似解，对于式(9)，可构建矩阵AX=b进行求解。

首先将桩体离散为m个节点，从桩顶开始，编号为r(r=1，2，3…，m)，每个节点的步长为h，同时桩头设置两个虚段0、-1，桩底设置两个虚段m+1、m+2。如图3所示。然后使用泰勒级数展开节点r+1和r-1的水平位移，如下：

(10)

(11)

忽略二阶无穷小量，将式(10)减去式(11)可得一阶中心差分公式：

(12)

忽略三阶无穷小量，将式(10)加上式(11)可得二阶中心差分公式：

(13)

同理可得三阶中心差分公式和四阶差分公式分别为：

(14)

(15)

图3 有限差分法划分单元体示意图

将式(9)化简如下：

Dk(z)q(z)

(16)

然后将式(12)—式(15)代入式(16)中得：

(Nrh2-4EI)yr-1+EIyr-2=Dkrqrh4

(17)

然后需要确定桩顶和桩底的边界条件，设桩身沿轴线方向任意一点r(深度zr)处的变形为yr，惯性矩为Ir，桩身弹性模量为Er，那么r点处的转角、弯矩、剪力可以表示为：

θr=(dy/dz)r

(18)

Mr=ErIr(d2y/dz2)r

(19)

Vr=-ErIr(d3y/dz3)r

(20)

利用式(12)—式(15)，式(18)—式(20)可以表达为：

4)相比传统日照分析方法，本文提出的方法操作过程简便，每一计算结果均有图形显示，清晰易懂。分析结果可为其它建筑物满足日照规范设计提供参考。

yr+1-yr-1=2hθr

(21)

yr+1-2yr+yr-1=h2Mr/ErIr=ξrMr

(22)

式中ξr=h2/ErIr。

yr+2-2yr+1+2yr-1-yr-2=-2h3Vr/ErIr=ψrVr

(23)

式中ψr=-2h3/ErIr。

通常情况下，对于桩底而言，根据桩身的受力特点，桩底弯矩很小，可以忽略不计，即可认为桩底处于铰接状态[12]，对于桩顶而言，根据桩顶荷载的形式不同，一般可分为桩顶自由，桩顶铰接和桩顶部分固定三种约束形式，如图4所示。

当r=1时，为桩顶节点，当r=m时，为桩底节点，根据式(21)—式(23)可得：

对于桩底铰接(水平位移和弯矩为0)

ym=0

(24)

(25)

对于桩顶自由(剪力和弯矩为0)

y3-2y2+2y0-y-1=0

(26)

y2-2y1+y0=0

(27)

对于桩顶铰接(水平位移和弯矩为0)

y1=0

(28)

y2-2y1+y0=0

(29)

对于桩顶部分固定，即上部结构对桩顶转动施加了一定的约束：

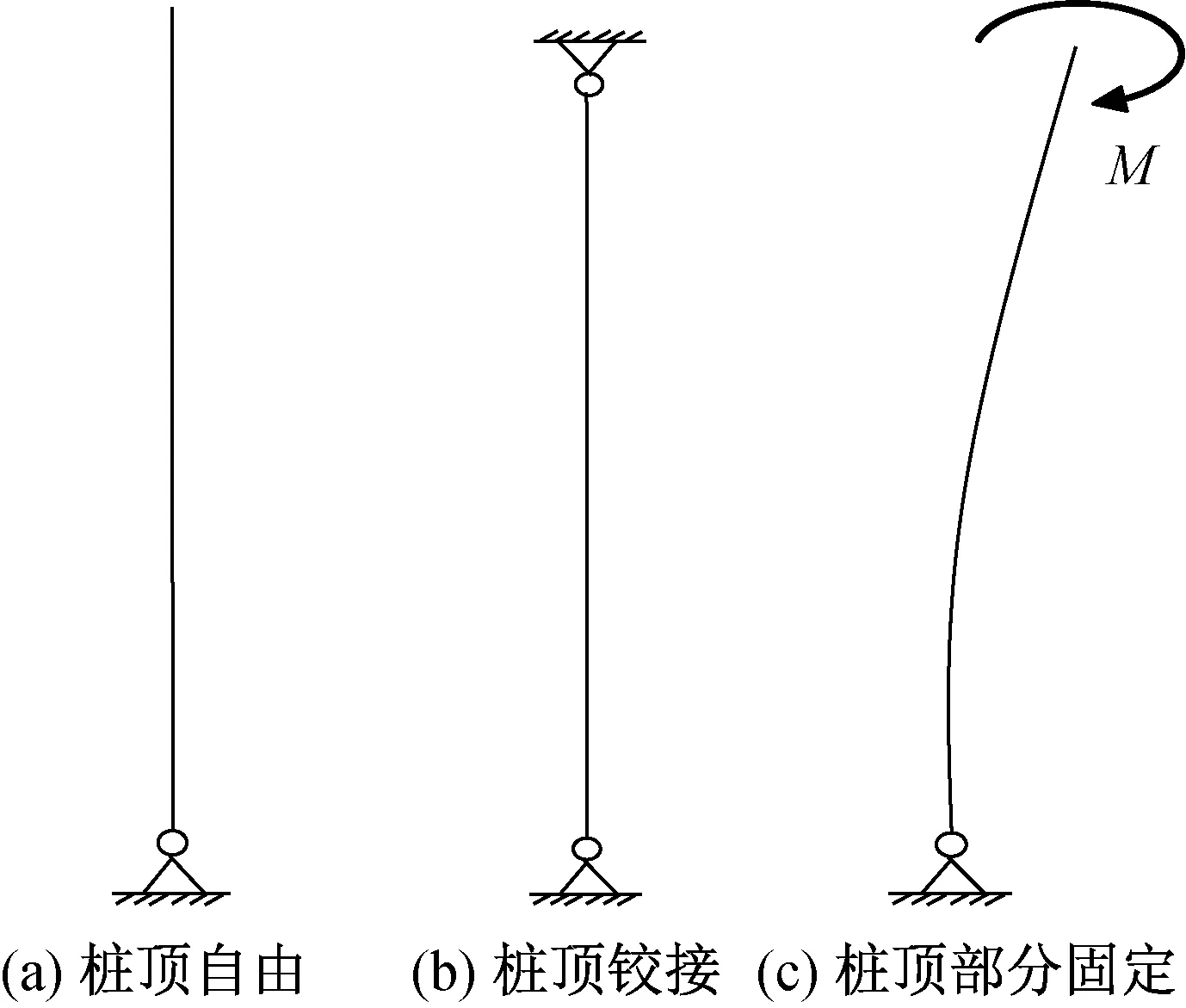
图4 桩身边界条件示意图

y2-y0=2hθ0

(30)

y2-2y1+y0=ξ0M0

(31)

那么针对不同的桩顶情况，矩阵方程组AX=b对应三种不同的表达形式：(1)当桩顶自由时，矩阵方程组AX=b可表示成式(32)；(2)当桩顶铰接时，矩阵方程组AX=b可表示成式(33)；(3)当桩顶部分固定时，矩阵方程组AX=b可表示为式(34)。

则y-1，y0，y1…ym，ym+1，ym+2，一共m+4个未知数，可由m+4个方程求得，即可以完成对隧道开挖下桩身挠度方程的求解，根据θ=(dy/dz)，M=EI(d2y/dz2)，V=-EI(d3y/dz3)，可分别计算桩身的转角、弯矩、剪力，由此，即可确定隧道开挖下桩土相互作用解答。然后采用MATLAB软件编制程序进行计算，可以得到某个深度处桩体响应。

(32)

(33)

(34)

4 工程计算实例

4.1 工程实例概况

为验证本文所提分析方法，分别采用本文解答和有限元对实际工程进行算例分析。算例选自文献[13]，该工程是位于上海市东北部的长江西路隧道开挖项目。隧道为连接宝山区和浦东区的公路隧道，起点位于黄浦江西岸，终点位于港城路与双江路交汇处。隧道全长4 912 m，主线长2 792 m。使用直径为15.43 m的大型盾构机，沿黄浦江东岸向西岸工作井推进，如图5所示。盾构机向前推进过程中高架道路的桩组，与相邻桩之间的最小距离为1.02 m。在隧道西岸开展了现场试验，以监测隧道施工对既有构筑物影响。

图5 现场工程示意图

4.2 试验介绍

试验主要关注隧道开挖过程中土和桩的横向移动。由于在隧道开挖过程中无法进行倾角测量，因此，在现场试验区隧道周围埋置四根预应力高强混凝土管桩，将测斜仪预先安装在管桩内，来监测桩身的变形，从而得到盾构机掘进过程中对邻近建筑物桩基的影响，试验桩相对位置如图6所示。

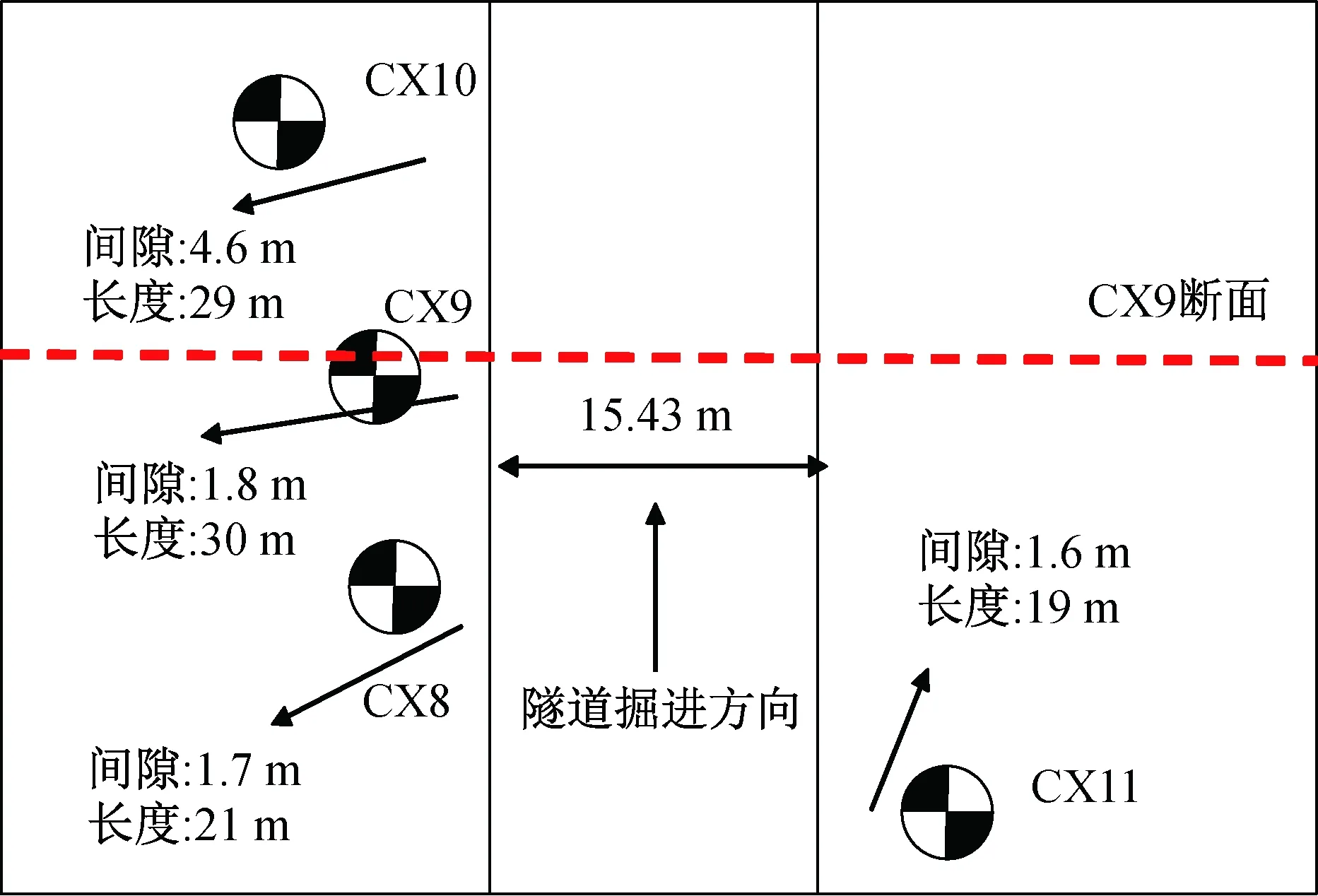
图6 试验桩相对位置示意图

4.3 有限元模型建立

从图6可以看出，CX9号桩距离隧道较近，并且桩身较长，桩身响应能够全面反映隧道开挖对周围地层的影响。所以本文选取CX9断面建立二维有限元模型进行分析计算。

模型中第⑦和⑨号土层为砂土，采用摩尔库伦模型，其余土层均采用修正剑桥模型，计算参数如表1所示，模型尺寸为165 m。两面约束水平位移，地面约束竖向位移，桩与隧道净距1.8 m，桩长31.8 m，隧道直径15.43 m，中心埋深24 m。模型示意图如图7所示。桩采用弹性本构模型。衬砌采用梁单元模拟衬砌厚度为0.65 m。衬砌与土体之间采用Tie约束，桩底面与土体之间采用Tie约束，侧面与土体之间采用摩擦约束。该模型共计4 377个单元，4 581个节点。

图7 二维模型示意图

4.4 计算结果分析

本文同时开展了解析解答和数值解答，然后将两者计算得到的桩身变形结果与实际监测结果进行比较。

使用相同的模型参数和相同的边界条件，建立了无桩情况下，隧道开挖对临近地层的影响有限元数值模型，将有限元计算得桩位置处的土体水平位移，作为土体自由位移场，然后进行解析解答的计算。如图8所示，当隧道周围没有桩基时，由于地层土层损失，周围土体成对称趋势向隧道中心移动，如图9所示，然后进行拟合，由于曲线较为复杂，将该曲线分成三段进行线性拟合，得本工程中隧道开挖下土体自由场水平位移表达式为：

(35)

本工程中的桩长为30 m，桩身节点个数本文确定为31个，计算步长为1 m，桩体弹性模量为3×104MPa，地基反力系数选择与实际工况较为符合的“C”法[14]进行计算，桩顶荷载为0 kN，忽略桩身轴力。同时确定桩身的边界条件，桩顶视为自由端，桩底视为固定端。将上述参数代入桩身扰度矩阵进行计算可以得到解析解答。

同时建立本工程实际的有限元二维模型，如图10(a)所示，当隧道开挖时，由于桩基的存在，隧道两侧土体的水平位移并不一致，左侧土体由于桩基的遮挡效应，水平位移较小。桩基的桩顶和桩底的水平位移较大，这导致介于隧道顶部和轴线之间的桩身部分挠曲变形较大。

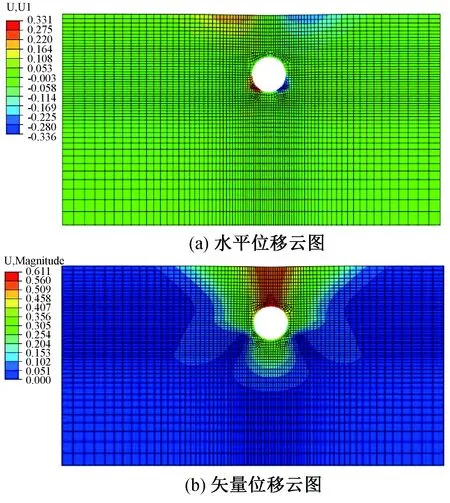
图8 无桩基存在时隧道开挖位移云图(单位：m)

为了便于比较桩身的变形，本文选择桩顶作为参考点即假定该处的水平位移为0，计算结果与实际监测结果如图11所示。由图可知，现场监测到的桩身侧向水平位移沿桩深分布不均匀，这是由于现场试验桩由多个翼板连接的分段组成。所以存在一定的离散性，规律性不强，但是监测值总体上还是呈现一定的规律性，与一般认知相符。

本文采用有限元数值模拟计算的结果和解析解答与监测值都较为接近。能够反映由于盾构施工引起地层位移并进而对既有桩基础的影响。

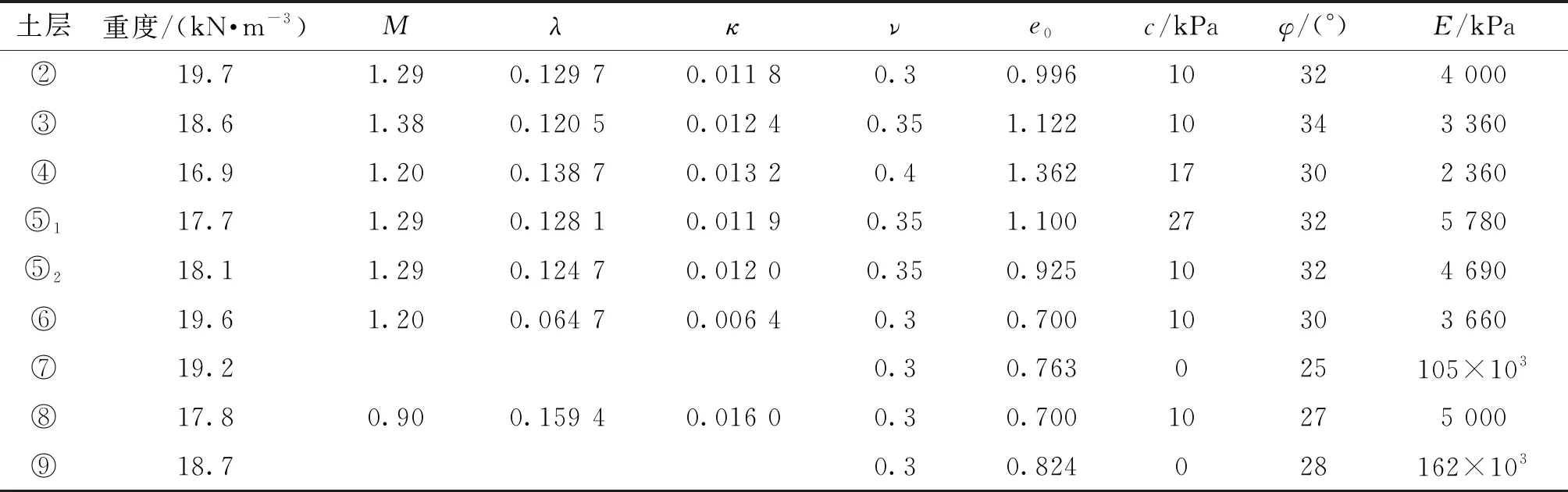
表1 土层及桩土接触参数的确定

图9 土体自由场

图10 有桩基存在时隧道开挖位移云图(单位：m)

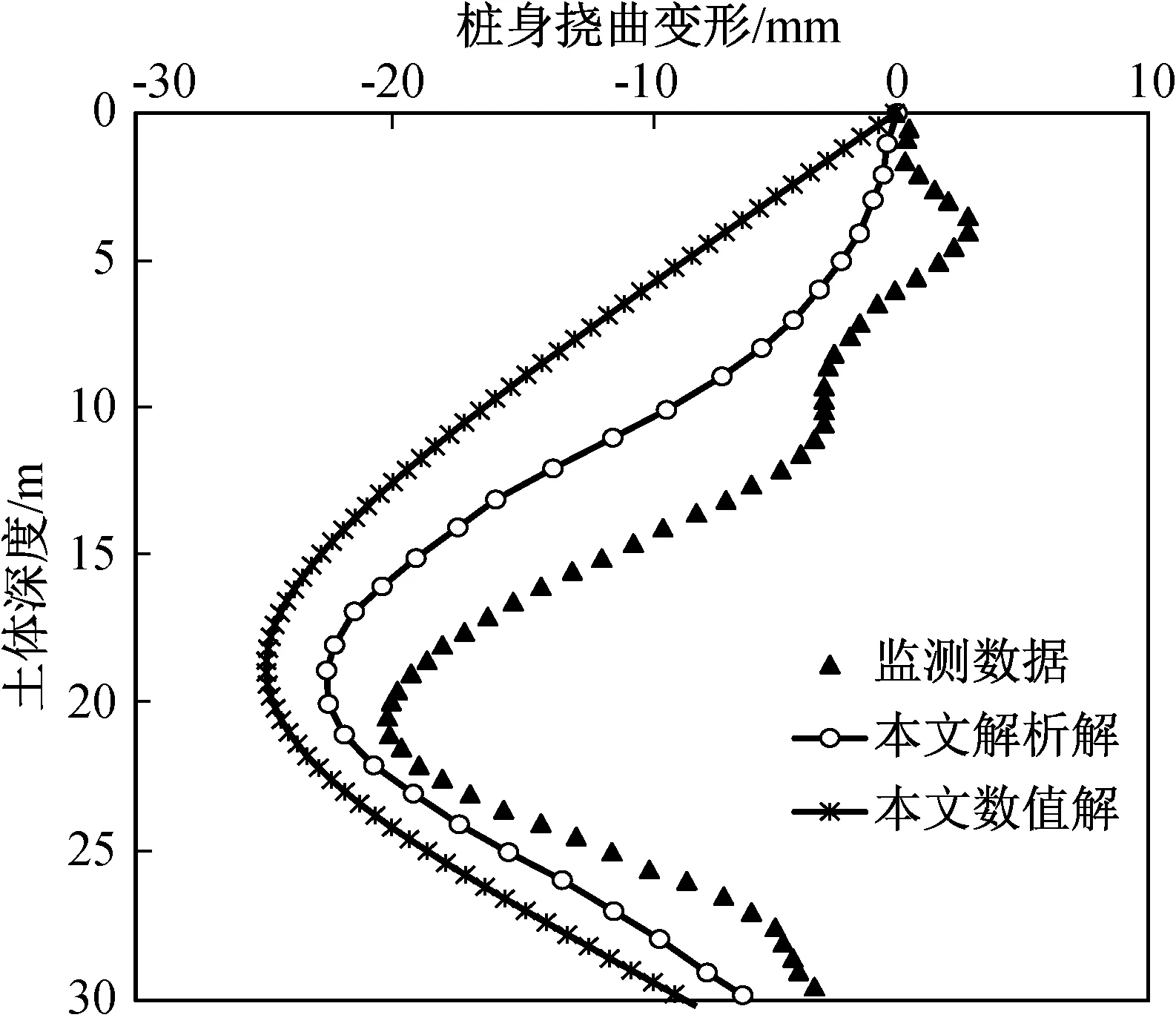
图11 计算值与现场监测结果

5 结论

本文建立了考虑不同桩体边界条件的桩土相互作用控制方程，以及基于有限差分的近似解答。依托实际工程，该解答与实际监测结果较吻合，证明其具有良好的工程实用性。