基于OpenFOAM求解聚合物加工的高Wi数流动*

陈迪林 张 来 李 捷* 陈海文 钱诗智

(武汉理工大学能源与动力工程学院1) 武汉 430061) (老道明大学微纳米技术学院2) 诺福克 VA23529)

0 引 言

黏弹性流体属于时变性非牛顿流体，具有黏性和弹性的双重特性，且广泛的存在于生活中的多个工业部门，如血液、油漆、高分子聚合物溶液、胶体溶液等，深入研究非牛顿流体的流动行为具有重要的工程应用价值[1].因此，黏弹性流体流动的分析与建模在工业领域中具有根本的重要性.黏弹性流体的流变响应非常复杂，包括非线性黏性和弹性效应的组合，剪切流中法向应力差的存在，弛豫现象和记忆效应，冲模膨胀特性等.关于黏弹性流动的数值分析，使用一个或多个非线性微分模型的分析处理方法在文献中都是常见的.无论离散化方法(有限元，有限差分或有限体积)，迭代求解方法或所用的本构方程，求解工作中的常见困难是所谓的“高Weissenberg数问题(HWNP)”. HWNP包含在高Weissenberg(Wi)或高Deborah(De)数下实现收敛的困难，其中量纲一的量化的参数Wi和De用以表征黏弹性流动的流动特征.

当下，商业的软件分析实际上仅限于纯黏性非牛顿现象描述，具有黏弹性流动分析能力的软件的开发和使用仍然几乎完全在学术环境中进行，应用于特定领域[2].OpenFOAM(open source field operation and manipulation)中新的求解器，对多弛豫时间、高Wi数问题、混合网格有着更大的适用性，并且支持并行运算与数据处理，在解决大网格尺寸的问题上有明显优势.作为一个经过充分测试和广泛使用的免费开源CFD软件包，更具有C++面向对象编程语言的内在优势，OpenFOAM软件包很明显是针对具体问题，开发自定义求解器的最有前途的工具.同时，处理非结构化和动网格以及实现复杂数学模型的灵活性，是其最吸引人的特征.

因此，于本文中，利用OpenFOAM软件包中的通用黏弹性流体求解器，采用一种基于分离应力张量方法[3]和平衡应力张量的概念去处理HWNP问题，且适用于任何微分本构方程.通过将其预测值与来自文献的实验数据进行比较来评估所谓的黏弹性流体求解器ViscoelasticFluidFoam，并用于分析平面4∶1平面收缩高Wi数流动与腰圆形形功能块流动的仿真分析.

1 DCPP本构模型与基本方程

1.1 数值模型

黏弹性流体等温不可压缩流动的控制方程是质量守恒方程(连续性)和动量守恒方程.

·(u)=0

(1)

(2)

式中：ρ为流体的密度；u为速度矢量；p为压力；τ为应力张量.应力张量可分为(溶剂)牛顿应力张量τs和弹性聚合物应力张量τp(或额外弹性应力张量)

τ=τs+τp

(3)

τs=2ηsD

(4)

(5)

式中：ηs为溶剂黏度；D为变形率张量；τpk取决于黏弹性流体的本构方程.

(6)

1.2 DCPP本构模型

考虑到欧湘萍等[4]提出的XPP模型预测稳态拉伸流和剪切流时存在解不唯一的问题,尽管有一些改进，但当包括非消失的第二正应力时，他们的新模型在简单的剪切流中遭受奇异行为，以上都是与实际高分子熔体的流变特性是不相符的.为了消除模型存在数学和流变学上的这些缺陷，Clemeur等[5]发展了DCPP模型，其本构模型描述为下述的形式.

(7)

式中：T为黏弹性额外应力张量；S为方向张量；Λ为拉伸量，用于表征Pom-Pom大分子的行为；I和G为单位张量、剪切模量；ξ为非线性参数，用于对第二法向应力差的控制.张量S和拉伸量满足下式.

(8)

(9)

式中：D为变形率张量，Δ和分别为上对流导数和下对流导数；λ和G为线性参数的范畴，λ为取向弛豫时间，λs为拉伸机制的弛豫时间；q依附于Pom-Pom大分子的支链数.其他的参数λs，q，ξ为非线性参数.

1.3 压力-速度、动量-应力耦合及张力黏度

速度-压力耦合是通过分离方法完成的，其中连续性方程(2)采用半离散形式，得到的方程组通过解耦方法求解，使用具有欠松弛的迭代算法，如SIMPLE算法[6].

为了保证动量方程解中的动量-应力耦合和数值稳定，所采用的策略包括将黏弹性应力分解为与D对应，基于张力黏度ηT定义的隐式分量，并进行显式校正.

·τ≈·(ηT·u)+·τcorr

(10)

此外，应力传递模型写成下面的通用形式：

(11)

该等式描述了应力随速度场在空间中的传递，同时在较小的弛豫时间后趋向平衡值τ*，其中τ*是在没有运输效应的情况下实现的应力状态，λ是松弛时间.无论使用任何特定的黏弹性本构模型，都可以实现这种形式.

根据定义导出，与所选模型无关的ηT表达式.

ηT=τ*·D-1

(12)

当detD=0时，意味着速度梯度是一个奇异张量.在以上的公式中，动量方程为

-p+·τcorr

(13)

1.4 数值算法

OpenFOAM中，用于求解黏弹性流体流动问题的方法可以归纳为以下四个步骤.

步骤1通过给定的初始速度u、压力p、应力τ，对压力梯度与应力差进行显式计算.随后隐式求解动量方程，得到一个新的速度预估值u*.

步骤2随着u*的计算，得到新的压力预估值p*，随后进行速度修正，得到新的满足连续性方程的新速度场u**.选择采用较好选择的SIMPLE或者PISO算法进行计算.其中，瞬态流动PISO算法更具有适用性.

步骤3随着修正后的速度场u**的计算，代入指定的本构方程中，求解得到应力张量场τ*.

步骤4瞬态流动中，前三个步骤每个时间步不断重复，能够生成得到更加精确的解.迭代过程中，u**，p*和τ*不断地获得更新.

动量方程(2)在OpenFOAM中的形式如下，具体的代码含义不做赘述，可以参考文献[7].

2 结果与讨论

2.1 收缩流几何和流动条件

通过与Clemeur等[8]的数据进行比较来测试DCPP模型的实施.图1所示的平面突然收缩， 2H=4.10 mm和2h=1 mm，收缩比为4.1∶1. 网格单元数为23 800，上游和下游流道长度分别为40，80 mm，以使其充分发展.使下游壁面剪切速率12.4 s-1，得到Weissenberg数为50.0.基于第一法向应力差N1(N1=τXX-τYY)定义主应力差PSD，用于参数比较.

图1 收缩流网格

(14)

表1中列出了DCPP模型参数的对应值.

表1 DCPP模型参数

2.2 DCPP的结果验证

运用Paraview后处理工具，展示了图2的等色条纹图.定值描述其变化趋势，速度值U与主应力差PSD的预测值见图3.结果表明沿着中心线y=0并且沿着于y=0.2,y=0.4,y=0.49获得了良好的收敛，除了收缩的入口有较小的偏差，但与Favero等[9]研究数据的误差不超过5%.主应力差与速度曲线都在一个较狭窄的范围内，沿着y=0.49的预测曲线不是特别理想，几何拐点的附近是否平滑，可能是导致预测值与实际差值的原因.PSD预测值与实验值趋势近似，但y=0线的最大值偏小，误差可能是由于收缩口前后网格不够细化所导致.文献[10]中网格在收缩处有半径为3 μm的圆角，而本文中忽略了圆角带来的影响.总体而言，仿真所得结果数据是令人满意并良好吻合的.

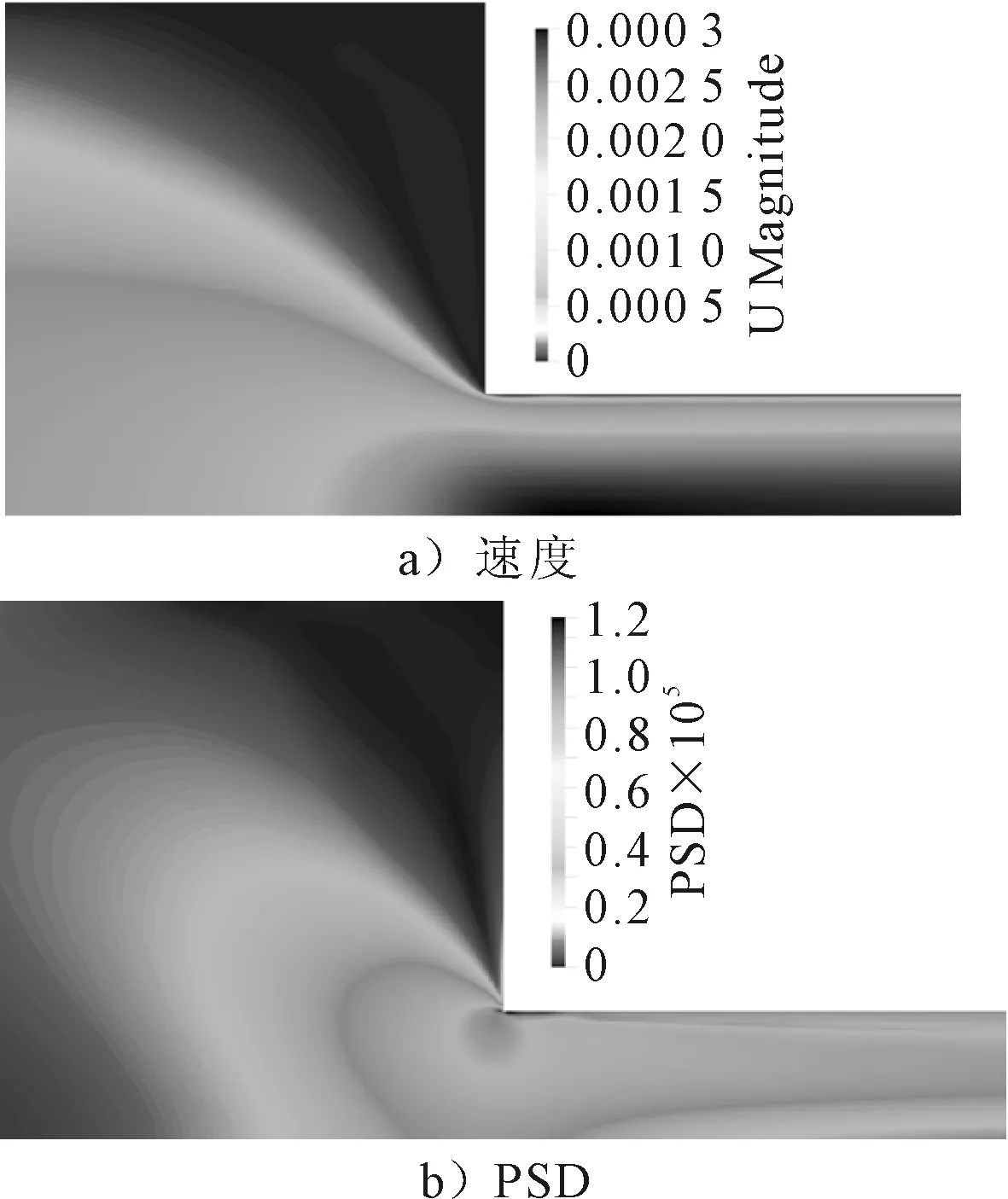
图2 速度和主应力差等色条纹图

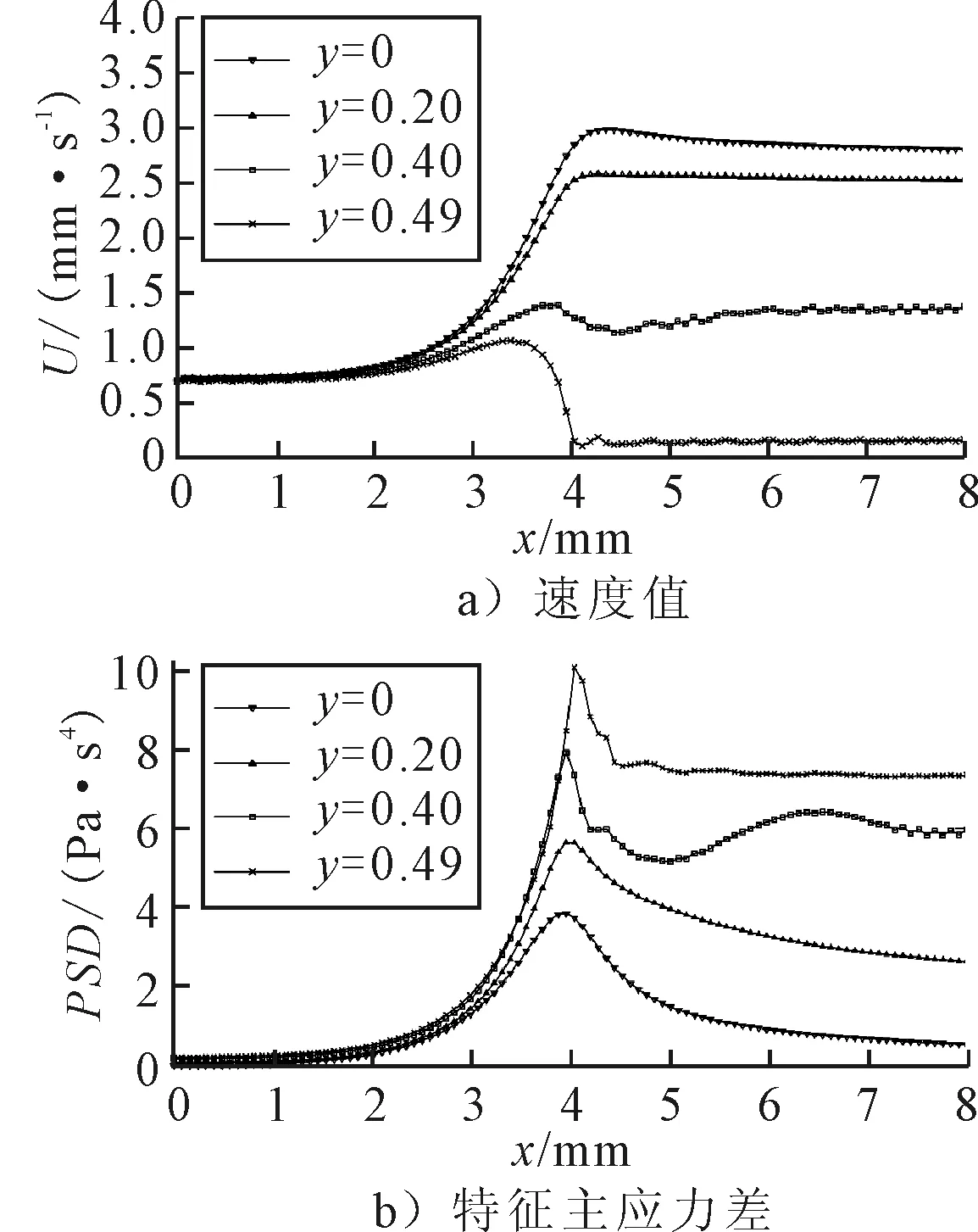
图3 收缩前后的速度值和特征主应力差

2.3 腰圆形功能块收缩流动的数值模拟

求解模拟聚合物在复杂流动几何中的流动，关键在于选取合适的黏弹性流体本构模型.DCPP是基于Pom-Pom的优化模型，能够很好的规避剪切流动中的奇异行为，预测聚合物溶液流动的拉伸和剪切作用.本节选用DCPP本构模型，针对注塑成型过程中腰圆形功能块收缩流动，对其流函数、速度、压力、主应力差进行了仿真，并与不存在嵌件的流场数据进行对比分析.

模型收缩比4.1∶1.腰圆形处L=1 mm，总长2 mm，圆弧半径r=0.5 mm，见图4.在腰圆形壁面及前后流场进行局部网格加密，网格数30 533.Wi数50，模型参数按照2.2选取.选用流量边界条件，固壁边界，定值压力出口，其他设为零梯度.

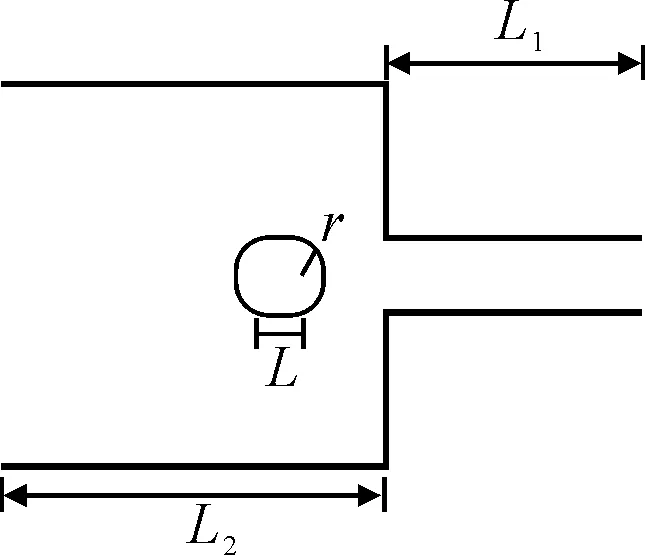
图4 腰圆形功能块几何

由图4可知，为收缩流道不存在功能块与存在功能块流场的数据对比图.图5为收缩口前后的流线图.很明显，在功能块的作用下，流体流线在中心线两侧发生分离；在功能块的上平面与下平面区域，流线近似平行于轴(X)方向流动，进入收缩口之前都紧紧的贴合于功能块壁面流动，两边绕行之后在功能块后侧进行汇合；图中可见，功能块的圆弧过渡段，由于不存在几何尖角，流线在流过功能块之前方向偏转.近二次涡流横截面上流线更加紧密，是由于功能块导致的收缩口前的又一次收缩，分子链在这一区域也会有大的强拉伸剪切行为.流体流过功能块后侧时发生急剧的方向偏转，是由于横截面积的急剧收缩及二次涡流的影响，将使流线更加集中，流速逐渐升高，这样的流动变化与实际工程中聚合物成型的规律是极其吻合的.

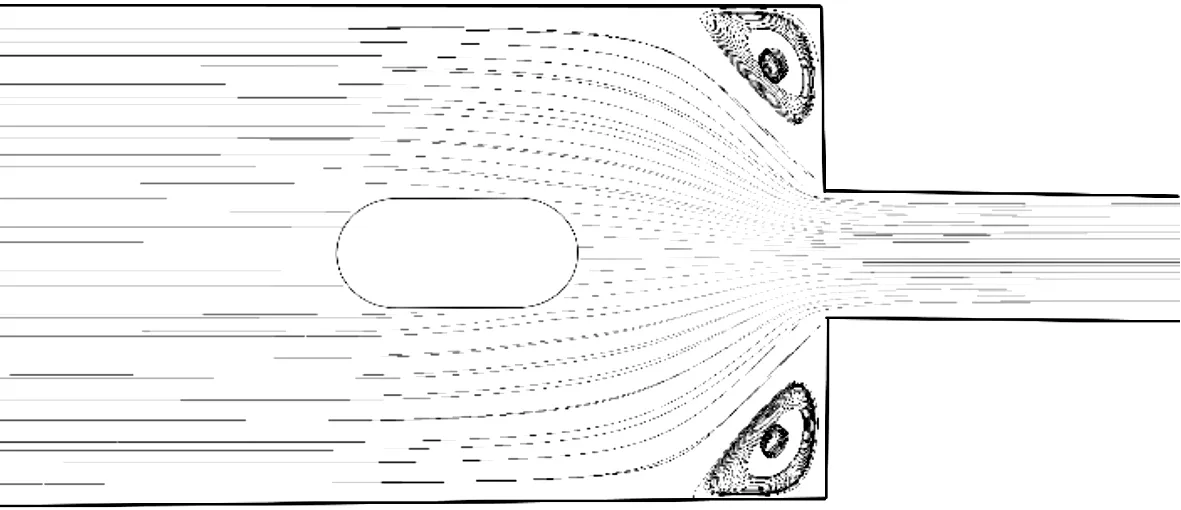
图5 流函数

图6为y=0与y=0.4上速度U的对比图.

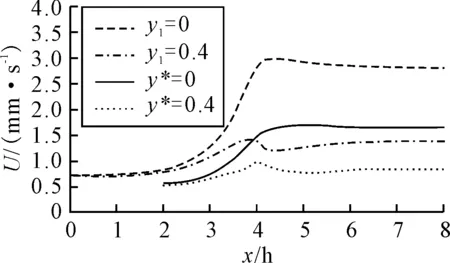
图6 速度趋势

y=0为中轴线上的速度，在功能块的作用下，无论是近壁面(y=0.4)还是中心线(y=0)上，都经历了一个巨大的速度损失；相较而言，在中心线流道上，速度U在功能块与收缩口之间的管段速度下降较少，更大的速度损失是在收缩口之后的管段；在近壁面处，速度U在收缩口前后的速度U几乎是同比下降，趋势近似；中心线趋势变化的原因：流体绕过功能块顶部后又进入了一个比较狭窄的通道内，大分子链有一个剪切到拉伸的过程，且块后局部流体受到上下分开的流道内的流体挤压，速度进一步降低，导致了收缩口后中心线上的速度损失更大；近壁面处，由于流体都是通过宽的流道随着流线而过，流动中受到的阻力更小，因此速度损失较小，几乎是同比下降.

图7a)为y=0和y=0.4在收缩口前后的压力降(图中y1为收缩流道预测值，y*为功能块收缩流道预测值).由结果可得在收缩口前后遭遇了大的压力损失，无功能块的近壁面压力曲线与中心流道压力曲线重合，存在功能块的情况下的预测值与收缩流道的趋势一样，也遇到了重合的预测曲线；可见对于压力p的预测值皆获得了良好的收敛，与实际情况下的压力变化吻合.

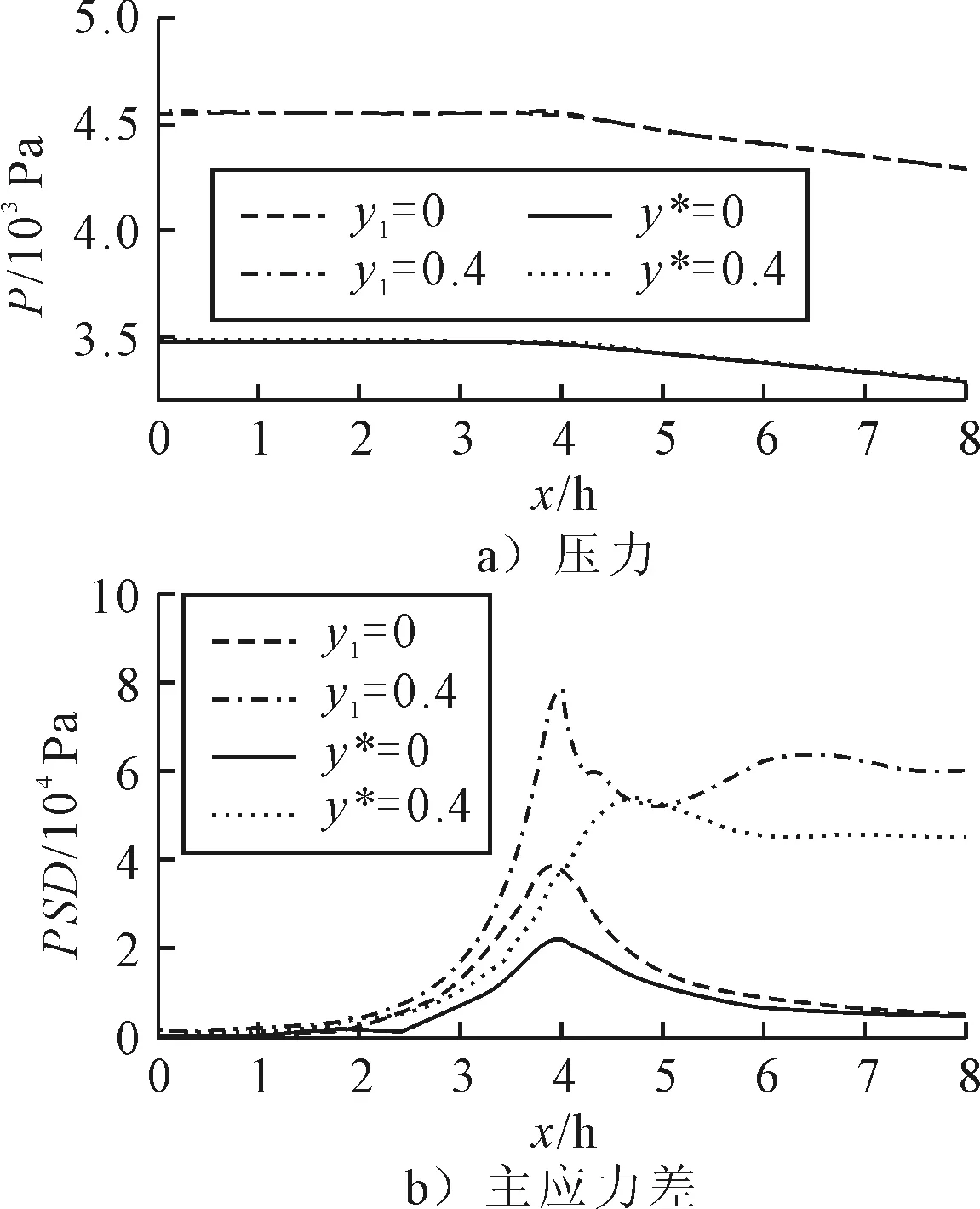
图7 腰圆形功能块收缩流动的压力与主应力差对比

图7b)为y=0与y=0.4在收缩口前后的主应力差PSD的预测值.预测的数值在中心线流道y=0上获得了良好的收敛，靠近壁面的预测值则不是那么理想，在收缩口下游拐角后流道有大的偏差与波动；功能块的出现导致了主应力差有部分降低.根据预测值的表征，具有弯角的功能块使得收缩口后半段的应力差波动越加稳定，并没有y1=0.4后半段波动那么明显.功能块后段流域,第一法向应力差与拉伸量同比变化，且取值较大.这是由于在功能块后侧,收缩流道中的二次回流，将增大分子链拉伸量，表征为聚合物分子弹性的增强，漩涡产生了一个强剪切作用的区域；在流过功能块与壁面的小收缩区域后，分子链部分弹性增强，当还未完全松弛的情况下，又经过回流区域的强拉伸区域及收缩拐角的剪切拉伸作用，聚合物弹性得到进一步增强.因此，主应力差的最大值出现在这一区域；另外一方面，在靠近壁面处的第一法向应力差的最大值较纯收缩流动的最大值有所滞后，主要是由于通道截面的多次急剧变化以及回流的作用，使得分子链向平衡态舒缓的过程变慢，剪切作用的叠加与拉伸舒缓的双重效果，共同形成了极值的滞后；在收缩口下游区域，流道得到充分发展，流场中剪切拉伸作用逐渐弱化，分子链进一步松弛，靠近壁面流体，由于受到拐角的扰动更大，向平衡态舒缓的速度更慢，而中心线附近流体则舒缓较快，二者都表征为第一法向应力差的逐渐减小.

3 结 束 语

本文中网格收敛与流动趋势、数值预测方面表现良好，确认所采用的方法是成功的；同时针对聚合物加工过程中常见的腰圆形功能块收缩流动，对流函数、U、PSD等聚合物浓厚体系表征量进行了预测分析，并与不存在功能块的流场数据进行对比，揭示其内部规律与机理，能够更好的服务于聚合物成型、模具优化、缺陷防范的相关研究；本文选用开源OpenFOAM工具，其所具有的优势与内在属性，能够高灵活性的求解黏弹性流体流动的相关问题，为黏弹性流动的开发应用提供巨大潜力.