列车延误条件下城市轨道交通跳停方案研究*

户佐安 夏一鸣 郑 磊

(西南交通大学交通运输与物流学院1) 成都 611756)(西南交通大学综合交通大数据应用技术国家工程实验室2) 成都 611756)

0 引 言

城市轨道交通列车的正常运行容易因各类突发事件产生延误，而较长时间的延误则会导致列车大面积晚点和站台乘客滞留.在这种情况下，常规的站站停运行调整模式已经不能很好地满足尽快恢复列车正常运行的要求[1].而跳停调整模式相较于站站停调整模式，能够使列车通过跨站运行从而更快地恢复至计划运行状态，但同时也会导致部分乘客无法及时乘降，增加其乘车及候车时间.现阶段城轨列车跳停方案的制定主要还是依据于调度员经验及预案，在全局性上还存在不足.因此，为了制定更为合理的跳停方案，在恢复列车正常运行的同时尽可能缩短乘客的旅行时间，建立行之有效的列车运行调整模型和相应求解算法就具有十分重要的意义.

国内外学者针对城市轨道交通列车跳停问题已展开一定的研究.郑锂等[2]对列车停站方案进行分类组合，建立了以乘客总出行时间节省最大为目标的0-1规划模型，并通过算例验证了模型的有效性.王婵婵等[3]从延误情况下多线换乘站的工况、跳停需求、跳停方案影响因素，以及跳停效果等方面进行分析，得出列车延误时在多线换乘站的跳停方法，并通过实际案例分析了该方法的局限性.刘祥喜[4]对各类突发大客流的特征进行分析，选取实际案例进行客流预测，并建立了以运营效率最高为目标的停站方案优化模型，最后提出突发大客流背景下的列车运营组织策略.Cao等[5]以列车停站状态为决策变量，建立乘客出行时间及列车总运行时间的总节省量最大为目标的0-1规划模型，并通过实例验证了模型的有效性.Freyss等[6]采用近似连续法将列车跳停问题用线路的站点密度等连续参数进行描述，并构建以列车运行成本最小为目标的运行调整模型，最后对跳停策略适用情况进行总结.Jamili等[7]对动态客流条件下的列车跳停方案进行研究，设计了一种将分解算法及模拟退火算法相结合的混合优化算法，并用实例证明该算法的稳定性.

综上，现有研究大多都是针对于常规情况下的城轨列车跨站停车问题，跳停方案采用固定的列车分类组合停站模式，且没有考虑因列车运能不足而使乘客滞留的问题.而在延误条件下，列车之间的运行调整空间小，且站台乘客容易出现积压，跳停方案的制定还需要考虑列车运行安全及列车运能利用情况等等因素，因此现有研究成果并不适用于延误条件下的列车跳停问题.本文基于某一列车延误条件，以乘客总旅行时间最小为优化目标，考虑列车运能约束、运行约束，以及跳停约束，建立相应模型与算法，以期制定更加灵活且合理的城市轨道交通列车跳停方案.

1 问题描述

1.1 跳停影响分析

列车跳停是指载客列车抵达某站后不进行停车操作，直接运行通过此站，图1 为列车跳停示意图.跳停对乘客出行的影响主要体现在以下三个方面.

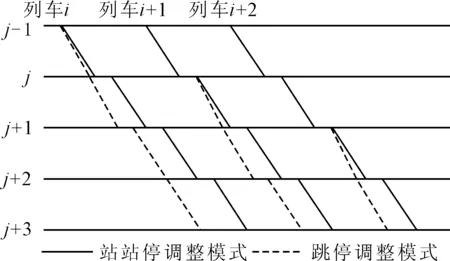
图1 列车跳停示意图

1) 跳停可以节省列车i在跳停站j的停站时间及起停附加时间，从而减少部分乘客的乘车时间.

2) 跳停会导致出行起始站为跳停站j的乘客无法及时上车，使其必须等待下一趟同向列车i+1才能上车，增加其候车时间.

3) 跳停会导致出行终到站为跳停站j的乘客无法及时下车，而乘客在提前得知跳停信息后会出现两种选择：①在跳停站的前一站j-1下车，此时乘客需要额外花费一次等候下一趟同向列车i+1的时间，才能到达出行终到站；②在跳停站的后一站j+1下车，此时乘客需要额外花费从跳停站j乘至后一站j+1、在站j+1等候反向列车，以及乘坐反向列车到达站j的时间.

综上可知，跳停调整模式在提高部分乘客出行效率的同时也会对一些乘客的出行产生负面影响.因此，当某一列车发生延误时，如何制定使整个乘客群体出行效率最高的列车运行调整方案，是本文需要解决的主要问题.

1.2 问题假设

结合我国城市轨道交通实际调度情况，本文给出以下假设.

1) 列车在线路的首站及末站均不组织跳停，列车不能连续跳停两站，同一站点不能被连续跳停两次.

2) 列车在恢复正点运行后不再进行调整.

3) 某线路1 h时段内的站间OD数据已知，且各站客流的到达服从均匀分布.

2 城市轨道交通列车运行调整模型

2.1 参数定义

模型相关参数定义见表1.

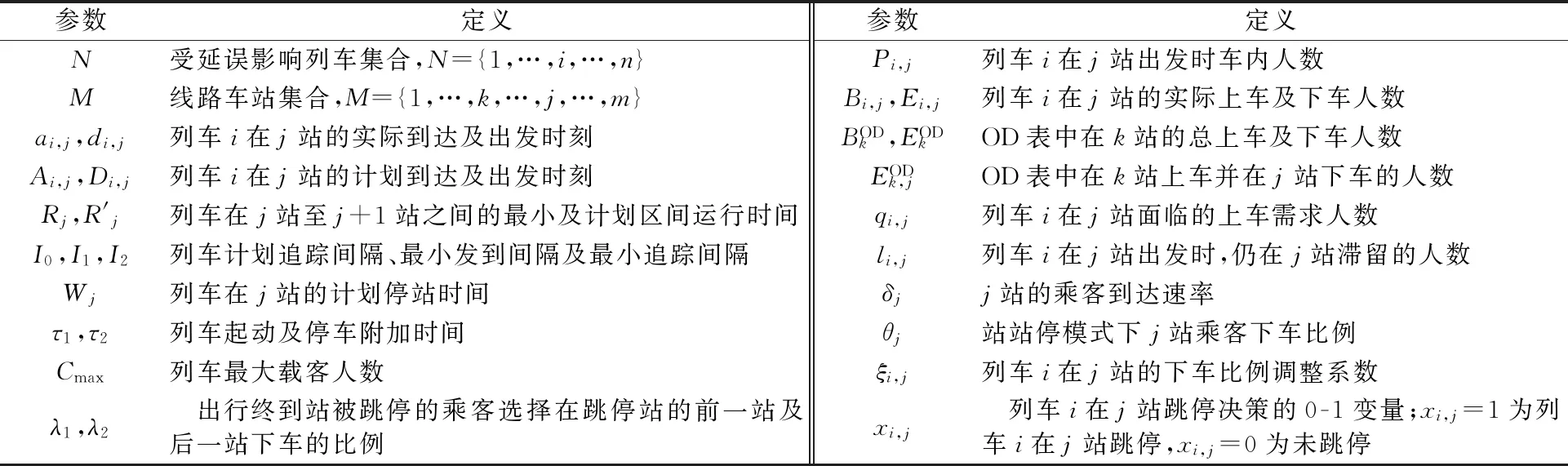
表1 参数定义

2.2 模型相关参数计算

本文将用列车出发时车内人数、上车需求人数、实际上车人数、实际下车人数，以及车站滞留人数来描述客流与列车运能之间的交互关系.

列车i在j站出发时的车内人数与其在j-1站出发时的车内人数及在j站的上下车人数有关，即

Pi,j=Pi,j-1+Bi,j-Ei,j

(1)

列车i在j站的实际上车人数决定于列车在该站的剩余载客能力能否满足上车需求，以及列车在该站的跳停与否，即

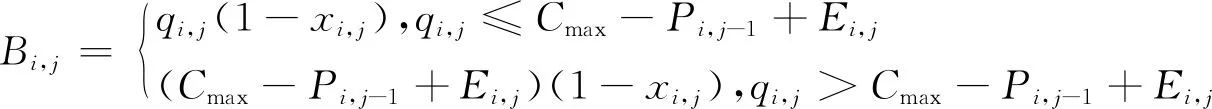
(2)

式(2)中上车需求人数即为列车i-1在j站出发时的滞留人数与在时段[di-1,j,di,j]内到达j站的人数之和，为

qi,j=li-1,j+δj(di,j-di-1,j)

(3)

式(3)中j站乘客到达速率δj可由OD表中的数据直接求出，即

(4)

由跳停影响分析可知，列车i在j站的下车人数与列车i在j站、j+1站以及j-1站的跳停与否有关，即

Ei.j=(Pi,j-1·θj·ξi,j+λ1·Pi,j·θj+1·ξi,j+1·

xi,j+1+λ2·Pi,j-2·θj-1·ξi,j-1·xi,j-1)(1-xi,j)

(5)

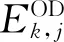
(6)

(7)

列车i离开j站时，j站滞留人数与列车i在j站面临的上车需求人数、实际上车人数以及可能因跳停在j站提前下车的人数有关，即

li,j=qi,j-Bi,j+λ1·Pi,j·θj+1·ξi,j+1·xi,j+1

(8)

2.3 目标函数

研究目标是使乘客总旅行时间最小，乘客总旅行时间表示为T.乘客总旅行时间可分为站台候车时间及乘车时间，分别表示为T1和T2，两者计算为

(9)

(10)

式(9)中，第一项表示正常乘客候车时间，第二项表示滞留乘客候车时间，第三项表示乘客换乘反向列车时的候车时间，此时平均候车时间取I0/2；式(10)中，第一项表示车内乘客站间乘车时间，第二项表示列车停站过程中不下车乘客的等待时间，第三项表示乘客乘坐反向列车时的乘车时间.

优化目标即为

minT=T1+T2

(11)

2.4 运行约束

运行约束条件有：

di.j=ai,j+wj(1-xi,j)

(12)

ai.j≥di,j-1+Rj-1-τ1·xi,j-1-τ2·xi,j

(13)

ai+1,j-di.j≥I1

(14)

ai+1,j-ai.j≥I2

(15)

di+1,j-di.j≥I2

(16)

di,j≥Di,j

(17)

式(12)为停站时间约束，由于缩短停站时间可能会导致积压的乘客无法及时乘降，因此本文不对停站时间进行调整；式(13)为列车区间运行时间约束，即列车i在j-1站跳停则可节省起动附加时间τ1，在j站跳停则可节省停车附加时间τ2；式(14)为列车最小发到间隔约束；式(15)为列车最小到达间隔约束；式(16)为列车最小发车间隔约束；式(17)为列车发车时刻约束.

2.5 跳停约束

跳停约束有：

xi.1=xi.m=0

(18)

xi.j+xi.j+1≤1

(19)

xi.j+xi+1.j≤1

(20)

式(18)为列车不能跳停首尾站；式(19)为列车不能连续跳停两次；式(20)为同一站点不能被连续跳停两次.

3 求解算法

目标函数及部分约束条件为非线性，而遗传算法具有优秀的全局搜索能力及处理非线性系统优化问题的能力，因此采用遗传算法求解[8].但由于本文决策变量中，跳停变量的取值直接决定着列车的到发时刻关系，导致两种变量无法同时参与迭代.为解决上述问题，设计了一个内外层嵌套式遗传算法，即外层遗传算法对停站方案进行优化，内层遗传算法基于外层的停站方案对到发时刻方案进行优化.具体流程见图2.

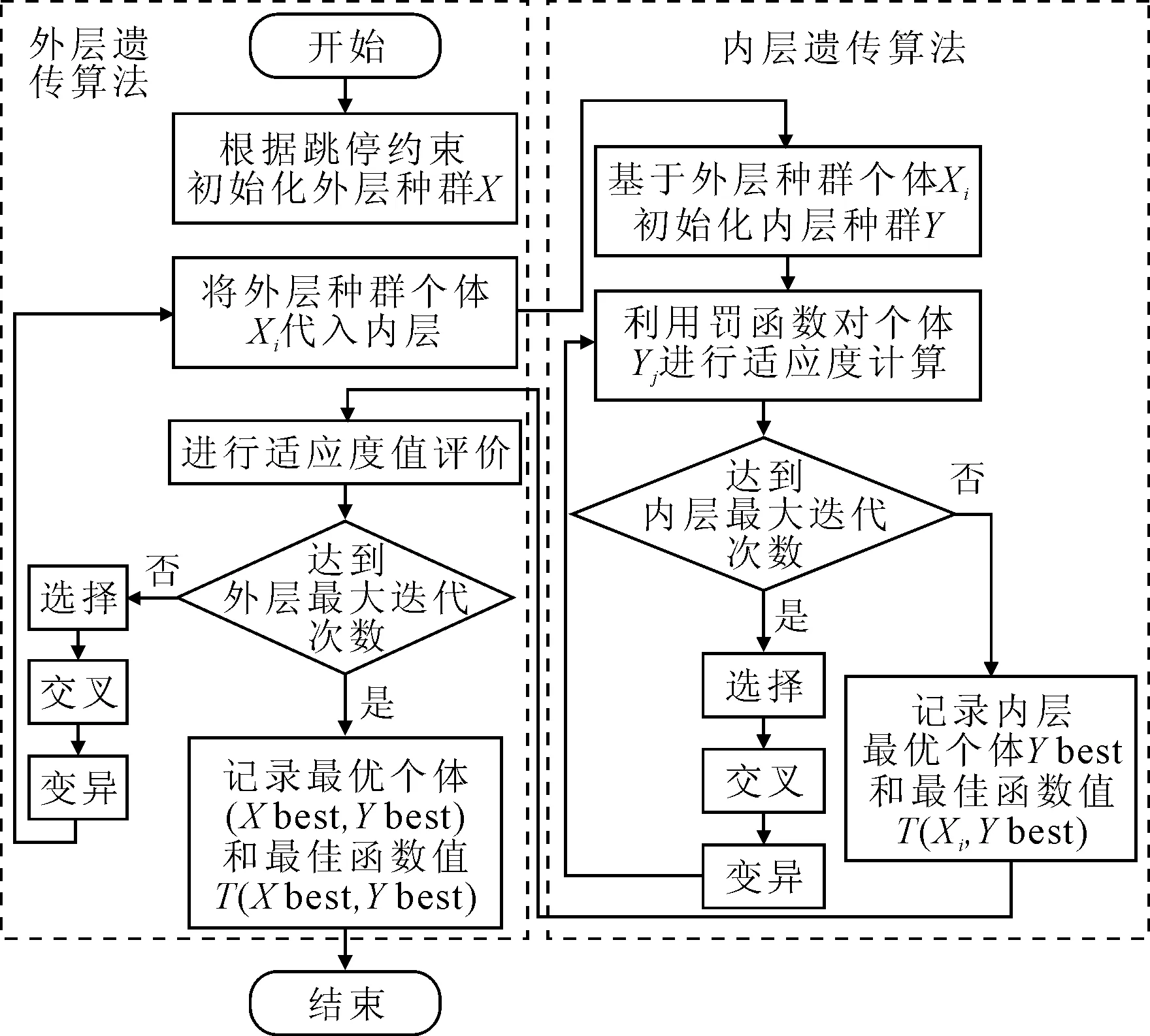
图2 嵌套式遗传算法求解流程

3.1 染色体编码及种群初始化

设外内层染色体分别为Xi和Yj，种群规模分别为S1和S2.其中:i=1,2,…,S1；j=1,2,…,S2.由于外层染色体由0-1变量构成，因此外层遗传算法采用二进制编码.为方便内层编码，本文将运行时刻表中的到发时刻转化为上午06:00:00至该时刻的间隔秒数，例如3 600即代表07:00:00这一时刻.由于内层染色体由正整数构成，因此内层遗传算法采用实数编码.外内层染色体结构见图3.

图3 外内层染色体结构

假设列车I在第Q站发生初始延误.对于外层种群的初始化，本文首先将染色体中第Q个及之前的基因全部设为0，随后从第Q+1个基因开始将其随机赋值为0或1，若违反跳停约束则令其为0.以此类推，直到形成符合跳停约束的个体Xi.循环上述操作S1次即形成初始种群X.

对于内层种群的初始化，首先分析跳停次数最大情况下以及站站停调整模式下各列车在各站的到达时刻，并将这两组时刻作为育种边界，以此生成染色体中代表到达时刻的基因，随后根据外层个体Xi和约束条件(12)生成代表出发时刻的基因，从而形成完整个体Yj.循环上述操作S2次即形成初始种群Y.

3.2 适应度函数

染色体适应度越大，表示其性能越好.因此内层个体Yj的适应度函数设计为

(21)

式中：C为一个足够大的正整数；nk(Xi,Yj)为基于外层个体Xi生成的个体Yj违反第k个运行约束的次数；p为惩罚因子且为正数.

外层个体Xi的适应度取内层最优个体Ybest对应函数值的倒数，即

Fit(Xi)=1/T(Xi,Ybest)

(22)

3.3 种群演变策略

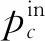
4 算例分析

4.1 基础数据

以某城市地铁线路为例.设线路共有20站，列车最大载客人数Cmax=1 400，计划追踪间隔I0=180 s，最小发到间隔I1=80 s，最小追踪间隔I2=120 s.假设某列车在第二站因突发事故产生初始延误，导致其在该站的出发时刻由08:01:40延误至08:11:40.根据延误时间可确定受延误影响列车数n=10.

当乘客的出行终到站被跳停时，由于在跳停站前一站下车的决策比在后一站下车所需额外花费的时间明显更少，因此本文设λ1=0.8，λ2=0.2.由文献[9]可知城轨列车起停附加时间均在15 s左右，因此本文设τ1=τ2=15 s.

只研究线路单向跳停方案，该线路08:00:00-09:00:00时段内的OD量,见表2.

表2 OD客流

设定的列车停站时间、计划区间运行时间及最小区间运行时间分别如下(单位为s).

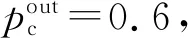
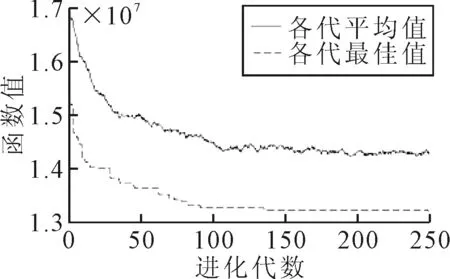
图4 函数收敛曲线

4.2 结果分析

优化后的列车运行调整方案见图5.

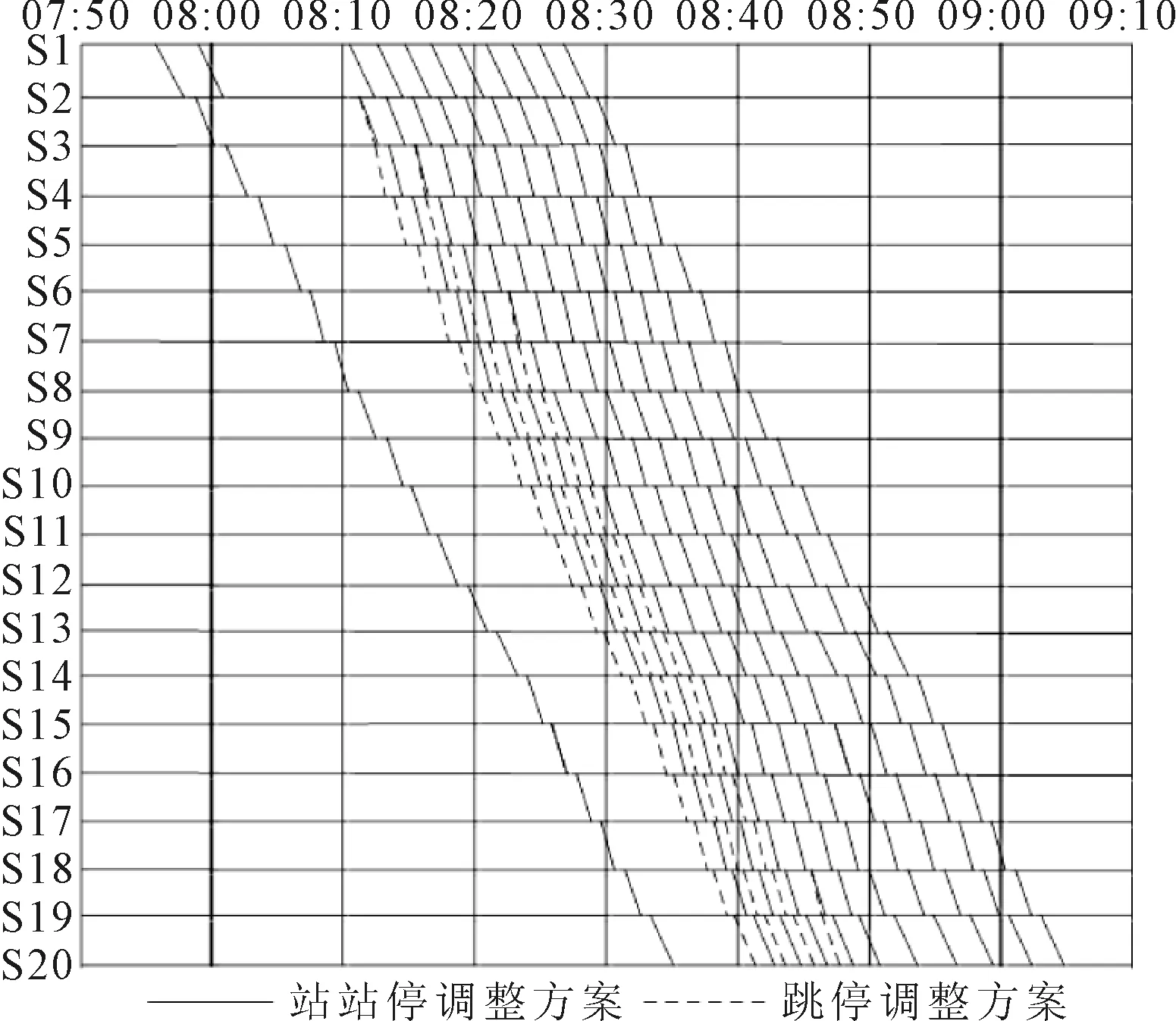
图5 两种调整方案下的列车运行图

为验证本模型的优化效果，将影响集合范围内，计划运行方案、站站停调整方案,以及跳停调整方案下的乘客总旅行时间、站台乘客候车时间与乘客乘车时间一一进行对比(各时间的单位由s换为h，以方便目标值的比对)，跳停调整方案相对于站站停调整方案的优化效果见表3.

由于算例中列车存在延误情况，且设定列车在恢复正点运行后均不再进行调整，因此跳停调整方案与站站停调整方案下得到的乘客总旅行时间必然大于计划值.但由表3可知，在站台乘客候车时间方面，模型求解得到的跳停调整方案相较于站站停调整方案，可以缩短6.6%因延误而产生的额外站台乘客候车时间；而在乘客乘车时间方面，模型求解得到的跳停调整方案和站站停调整方案相比于计划运行方案均能够有效缩减乘客的乘车时间，但跳停调整方案的缩减效果更加明显.最后在整体层面上，结果表明本模型求解得到的跳停调整方案能够显著减少64.8%由列车延误带来的额外乘客总旅行时间.由此证明，在列车延误条件下，建立的运行调整模型与算法在应对城轨列车运行调整问题上具有有效性及优越性.

表3 结果对比

5 结 束 语

文中从乘客的角度出发，分析列车跳停对乘客出行的影响，并结合城市轨道交通实际调度情况，考虑客流与列车运能之间的交互关系及列车延误情况下列车跳停需考虑的约束，建立了以乘客总旅行时间为目标函数的运行调整优化模型，并根据模型特点设计了嵌套式遗传算法来对模型进行求解.最后通过设计算例证明了本文模型及算法的有效性及优越性，可为城市轨道交通列车延误条件下的实际调度提供理论支持.文中研究的前提之一是客流的到达为均匀分布，这与实际情况略有差别，因此动态客流下跳停方案的制定有待进一步深入研究.