基于误差剔除和重标极差法的滑坡水平变形趋势分析
2020-10-18王承敏
王承敏,程 涛
(1.上海城地岩土设计有限公司,上海 200333;2.湖北理工学院 土木建筑工程学院,湖北 黄石 435003)
近年来,极端天气日益增多,极大程度上诱发了滑坡灾害。为保证威胁区内居民的生命财产安全,开展滑坡灾害的相关研究具有重要意义。滑坡变形是滑坡稳定性的直观体现,加之滑坡多沿纵向滑动,进而开展滑坡水平位移变形趋势研究的尤为必要[1-3]。目前,已有学者开展了滑坡水平位移方面的相关研究,如赵久彬等[4]利用数理统计,分析了滑坡水平位移与降雨量间的关系,为其空间预测提供了一种思路。成枢等[5]利用优化BP神经网络构建了滑坡变形预测模型,有效地实现了对滑坡水平位移变形规律的研究。上述研究虽取得了一定成果,但均未涉及滑坡水平位移的变形趋势分析,加之滑坡所处区域受地质条件限制,故仍有必要进一步开展滑坡水平位移变形趋势的研究。根据栗燊等[6]的研究成果可知,滑坡变形数据含有一定的误差信息,有必要对其进行剔除处理,且小波去噪和卡尔曼滤波[7]具有良好的数据处理能力,利用其实现滑坡误差剔除处理是可行的。同时,李秋全等[8-9]通过研究发现,重标极差法适用于滑坡变形趋势判断。
因此,本文以八字门滑坡水平位移数据为基础,先利用小波去噪和卡尔曼滤波实现其误差信息剔除,再利用重标极差法判断其水平位移变形趋势,以期为滑坡水平位移变形规律研究提供一种新的思路。
1 基本原理
滑坡水平位移变形趋势的研究思路为:首先利用去噪方法剔除滑坡水平位移数据中的误差信息,以求得滑坡水平位移的真实数据,保证后续分析的准确性;再以已处理好的数据为基础,利用重标极差法(Rescaled Range Analysis,简称R/S分析)进行滑坡水平位移的变形趋势判断。
1.1 误差剔除模型的构建
由于滑坡所处地质条件较为复杂,加之受监测过程中人为不确定因素的影响,滑坡水平位移数据往往含有一定的误差信息,即:
Yt=Xt+wt
(1)
式(1)中,Yt为滑坡水平位移监测数据;Xt为滑坡水平位移的实际变形值;wt为误差信息。
水平位移数据含有的误差信息会影响后续变形趋势判据结果的准确性,需要对其进行剔除处理。小波去噪和卡尔曼滤波2种误差信息剔除方法均具有良好的误差剔除效果,鉴于两者的适用性存在差异,因此为保证本文误差信息的剔除效果,通过对比分析两者在实例中的剔除效果,确定最佳误差剔除模型。
1.1.1小波去噪模型
小波去噪是通过函数空间映射的最佳逼近来实现误差信息剔除,具有较强的适用性,已被广泛应用于滑坡领域。结合其基本原理,其去噪过程可定义为:
(2)
式(2)中,f(a,b)为小波系数;ψ(t)为基本小波函数;b为平移因子;a为伸缩因子。
随着去噪理论及计算机技术的发展,传统小波去噪参数的经验设定已难以满足实际工程需要,其中,小波函数类型、阈值选取方法、阈值选取标准及分解层数等对去噪效果具有较大影响。因此,为保证去噪效果,有必要对上述参数进行优化筛选。
1)小波函数类型。在小波去噪方法中,小波函数类型较多,常用类型包括db小波系、cof小波系和sym小波系,且受小波阶次设定的影响,小波函数类型还可进一步细分。鉴于各类小波函数去噪条件存在差异,对其优化筛选是有必要的。
2)阈值选取方法。常用的阈值选取方法为软阈值和硬阈值。前者主要是按收缩处理边界上的不连续信息;而后者主要是全面剔除阈值标准以外的信号。两者的实现方式明显不同,因而确定合理的阈值选取方法也是必要的。
3)阈值选取标准。常用的阈值选取标准包括通用阈值、自适应阈值、启发式阈值和极限阈值4类,其原理各不同,因而也需进行优化筛选。
4)小波分解层数。小波分解层数过少,难以保证误差信息与真实信息的准确分离;反之,又可能将误差信息错当真实信息。因此,小波分解层数对去噪效果的影响较大,因而有必要进行优化筛选。
结合文献[6]的研究成果,启发式阈值和10层小波分解具有良好的去噪效果。在其研究基础上,将上述4类参数的优化过程设定如下:为保证筛选范围的全面性,将db小波系、cof小波系和sym小波系均纳入筛选范围,并将阈值选取标准设定为启发式阈值,分解层数设定为10层,小波阶次设定为3阶、5阶、7阶和9阶,通过试算确定最优阈值选取方法和小波函数。然后,再计算求解4种阈值选取标准的去噪效果,确定出最优阈值选取标准。最后,对分解层数为6~14层间的偶数层进行去噪效果分析,确定出最优分解层数。
1.1.2卡尔曼滤波模型
卡尔曼滤波是在线性空间状态基础上,通过输入信息与输出信息间的最优估计来实现误差剔除。由于不需要满足噪声与信号间的平稳假设,其适用范围较广,在岩土领域也有广泛的应用。根据应用经验,卡尔曼滤波递推过程易出现发散现象,不利于抵抗粗差影响。因此,为满足剔除误差的需要,发展出了多种卡尔曼滤波类型,主要包括标准型、半参数型、自适应型和抗差自适应型。由于各类型的适用性也存在一定差异,因此可以利用试错法确定最优卡尔曼滤波类型。
1.1.3误差剔除效果评价指标
误差剔除效果通常用平滑度、信噪比及均方根误差3种指标进行评价。由于各评价指标的评价侧重点不一致,为保证评价效果的准确性,利用三者构建综合评价指标g:
g=g1+g2+g3
(3)
式(3)中,g1~g3分别为平滑度、信噪比及均方根误差指标的归一化值,旨在避免各类基础指标单位差异影响。
通过对比综合指标g的大小来评价误差剔除效果:g值越大,说明误差剔除效果越好;反之,误差剔除效果越差。
1.2 水平位移变形趋势判断模型的构建
重标极差法已被广泛应用于岩土领域变形序列长期相关性评价,具有较强的适用性。利用重标极差法可实现对滑坡水平位移变形发展趋势的判断,其判断过程为[8]:
将滑坡水平位移序列设定为{Ni}(i=1,2,…,N),将其划分为A个长度为n的子序列,并将每个子序列设定为Na(a=1,2,…,A),对其进行均值求解,得均值为ea。
先对各子序列进行累计离差Xk,a求解,即:
(4)
式(4)中,Nk,a为子序列中的水平位移值。
在累计离差计算结果的基础上,求解各子序列的极差值Ra:
(5)
再对各子序列的标准差Sa进行求解,即:
(6)
通过上述极差和标准差可求得到各子序列的重标极差(R/S)a为:
(7)
最后,对所有子序列的重标极差进行均值(R/S)n求解,即:
(8)
由上可知,n值与(R/S)n具有对应关系,通过改变n值大小,即可求得若干散点(n,(R/S)n),且lgn和lg(R/S)n间具有如下线性关系:
lg(R/S)n=lgC+Hlgn
(9)
式(9)中,C为拟合常数;H为Hurst指数。
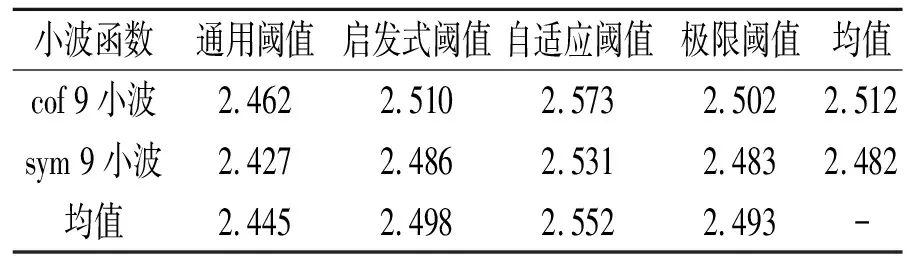
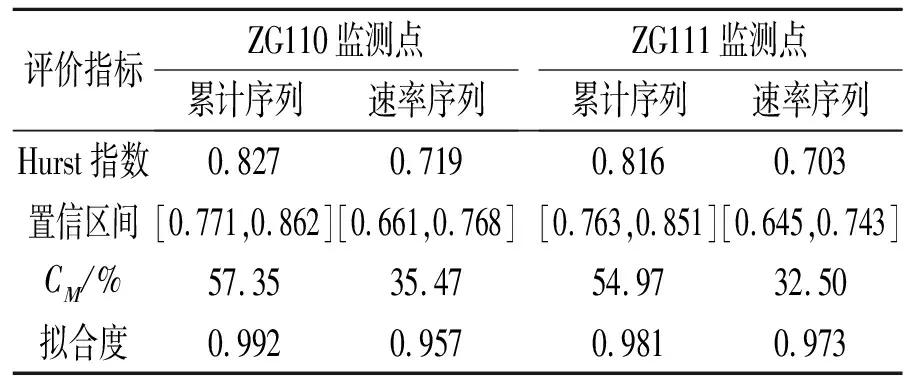
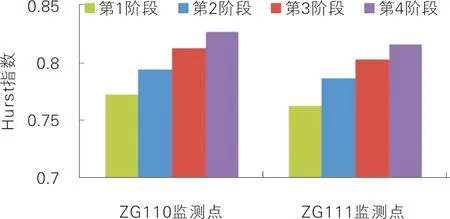
利用Hurst指数即可判断滑坡水平位移序列的变形趋势。当0.5 为实现滑坡水平位移序列的相关性评价,再引入CM统计量: CM=22H-1-1 (10) CM统计量可判断水平位移序列的相关性。当CM>0时,说明滑坡水平位移序列具有正相关性;反之,为负相关性,且CM值的绝对值越大,滑坡水平位移序列的相关性越强。 八字门滑坡隶属湖北省秭归县归州镇管辖,位于三峡库区香溪河右岸。其平面形态呈不规则扇形,剖面呈阶梯状,后缘宽度约105 m,前缘宽度约350 m,纵向长约517 m,总面积约11.78万m2,滑体厚度10~50 m,总体积约235万m3,属大型滑坡。 据现场勘查,滑坡区地势呈西高东低,且具有3级堆积平台地貌,致使其坡度变化较大,其中,后侧斜坡较陡处可达60°,中部平台处仅5°。据钻探结果可知,滑坡下部滑床主要以侏罗系香溪组砂泥岩互层为主,于滑坡后缘出露较多。滑带可分为主滑带和次级滑带2种。其中,次级滑带位于滑坡中部,埋深及岩性随位置差异变化,后缘埋深为6~18 m,主要以粉质粘土为主,在中部及前缘埋深为27~33 m,主要以碎石土为主;主滑带为基覆界面,埋深受滑体变化影响,呈前后薄、中部厚的特征,岩性以粉质粘土为主,夹杂少量角砾。滑体可分为上中下3层,其中,上层为填筑土,主要为坡体中部公路修建的弃土,厚度变化较大;中层为粉质粘土,褐红色,可塑至硬塑状态,厚度变化差异也较大,平均厚度约12 m;下层为碎石土,褐黄色,厚度间于6~50 m,平均厚度为30 m。 同时,由滑坡区水文调查结果得出,滑坡区内水文条件发育具体特征如下。 1)地表水。区内地表水主要以前缘香溪河为主,其水位受三峡库区水位调节影响较大,主要接受降雨补给;其次,河流两岸斜坡支沟也较发育,流水季节性变化较大。 2)地下水。按赋存条件可分为孔隙水和裂隙水,前者主要赋存于上部第4系地层孔隙,后者主要赋存于下覆基岩裂隙,均以降雨补给为主。 八字门滑坡于1982年出现复活迹象,加之2003年受三峡蓄水影响,滑坡变形历年增加,且在2008年至2011年间变形显著。八字门滑坡变形特征现状如图1所示。 (a) 滑坡后缘公路裂缝 (b) 滑坡中部拉张裂缝 为掌握八字门滑坡的变形特征,对其进行变形监测,其中,ZG110监测点位于滑坡中部,ZG111监测点位于滑坡后缘,在监测过程中,监测频率为1次/月,监测时间为2008年1月至2011年12月,共计得到48个监测周期数据,两者的监测结果较为完整,可将其作为分析的数据来源。滑坡水平位移变形曲线如图2所示。 图2 滑坡水平位移变化曲线 滑坡水平位移监测数据中含有一定的误差信息,会对后续变形趋势判断结果造成不利影响,有必要对其进行剔除处理。分别使用小波去噪和卡尔曼滤波对误差信息进行剔除,分析两者剔除效果。 2.2.1小波去噪误差剔除效果分析 按照小波去噪的参数优化流程,先将阈值选取标准设定为启发式阈值,分解层数设定为10层,得到不同小波函数在不同阈值选取方法下的误差剔除效果(见表1)。由表1可知,对比评价指标均值,不同小波系的误差剔除效果存在一定差异,得出cof小波系的误差剔除效果相对最优,sym小波系与之相当,两者都优于db小波系;小波阶次也对误差剔除效果产生影响,主要表现为随着小波阶次的增加,误差剔除效果相对更好;对同一小波系来讲,硬阈值的误差剔除效果也要优于软阈值的误差剔除效果。因此,考虑到cof小波系和sym小波系的误差剔除效果相当,初步确定小波函数为cof 9小波和sym 9小波,阈值选取方法为硬阈值。 表1 不同阈值选取方法的误差剔除效果 在确定了小波函数和阈值选取方法的基础上,再对4种阈值选取标准的误差剔除效果进行试算筛选。不同阈值选取标准的误差剔除效果见表2。 表2 不同阈选取值标准的误差剔除效果 由表2可知,不同阈值选取标准的误差剔除效果存在一定差异,验证了对阈值选取标准优化筛选的必要性。对比4类阈值选取标准的误差剔除效果得出,自适应阈值选取的误差剔除效果相对最优,其次是启发式阈值、极限阈值和通用阈值;对比cof 9小波和sym 9小波的去噪效果可知,前者的评价指标均值为2.512,优于后者的2.482。因此,根据上述筛选结果,确定小波函数为cof 9小波,阈值选取标准为自适应阈值。 根据小波去噪参数的优化步骤,对分解层数6~14层间的偶数层误差剔除效果进行试算分析。不同分解层数的误差剔除效果见表3。由表3可知,不同分解层数的误差剔除效果也不尽相同,随分解层数增加,评价指标g近似表现为先增加后减小趋势,且在12层分解时的误差剔除效果相对最优,进而确定小波分解层数为12层。 表3 不同分解层数的误差剔除效果 根据上述小波参数的优化筛选,确定最优参数为cof 9小波、硬阈值选取方法、自适应阈值标准和12层分解,其综合评价指标g值为2.638。 2.2.2卡尔曼滤波误差剔除效果分析 类比上述小波去噪的优化筛选过程,对4种类型的卡尔曼滤波进行误差剔除效果筛选。不同类型卡尔曼滤波的误差剔除效果见表4。由表4可知,不同类型卡尔曼滤波的误差剔除效果具有明显差异,验证了卡尔曼滤波类型筛选的必要性。由表4可以得出,半参数型卡尔曼滤波的误差剔除效果相对最优,其次是抗差自适应型、自适应型和标准型。因此确定卡尔曼滤波的最优误差剔除类型为半参数型,其综合评价指标g为2.538。 表4 不同类型卡尔曼滤波的误差剔除效果 对比2种误差剔除方法的误差剔除效果得出,小波去噪在最优参数条件下的综合评价指标为2.638,优于半参数型卡尔曼滤波的2.538。因此,确定本文误差剔除方法为小波去噪,相应参数为cof 9小波、硬阈值选取方法、自适应阈值标准和12层分解。 以误差剔除处理后的数据为基础,对其进行重标极差分析,判断滑坡水平位移的变形趋势。为保证分析结果的全面性,对滑坡累计变形序列和变形速率序列均进行变形趋势分析。滑坡水平位移变形趋势判断结果见表5。 表5 滑坡水平位移变形趋势判断结果 由表5可知,2个监测点不同序列的Hurst指数均大于0.5,说明八字门滑坡水平位移具有正向持续性,其变形发展趋势与现状发展趋势一致,呈持续增加趋势。对于同一个监测点,累计序列的Hurst指数均不同程度地大于速率序列的Hurst指数,说明累计序列较速率序列具有相对更强的趋势性。对于同一分析序列,ZG110监测点的Hurst指数大于ZG111监测点的Hurst指数,说明前者变形的趋势性相对更大,结合监测点位置,得出八字门滑坡中部位移较后缘位移的变形趋势更为明显。在相关性评价方面,2个监测点均具有正相关性,且累计序列较速率序列具有相对更强的相关性。在拟合效果方面,2个监测点在不同序列的拟合度均趋近于1,说明趋势判断过程的拟合效果较优,分析结果的可信度较高。 为进一步分析八字门滑坡水平位移变形的阶段性特征,再将其监测过程等分为4个阶段,每阶段12个周期,分析得到累计序列和速率序列在不同阶段的Hurst指数。不同阶段的变形趋势对比如图3所示。 由图3可知,随着时间的推移,累计序列的Hurst指数呈不同程度的增加,而速率序列的Hurst指数则不具特定规律,波动性较强,但两序列的Hurst指数均大于0.5,说明在本次监测时间内,八字门滑坡的水平位移累计值具有持续增加趋势,但其增加速率存在一定差异,这与变形曲线一致,验证了变形趋势判断结果的准确性。 (a) 累计序列 (b) 速率序列 通过上述分析可知,八字门滑坡的水平位移变形仍将继续增加,建议采取切实措施控制滑坡变形发展,保证航运及区内居民安全。 通过对八字门滑坡水平位移变形数据进行误差剔除和变形趋势分析,主要得出如下结论。 1)滑坡变形影响因素较多,其变形监测数据含有一定的误差信息,为保证数据分析结果的准确性,有必要对其进行误差剔除处理,且小波去噪和卡尔曼滤波均能较好的剔除滑坡水平位移数据中的误差信息。 2)重标极差分析能有效判断八字门滑坡的水平位移变形趋势,得出水平位移的累计值呈持续增加趋势,但其增加速率存在一定差异,且后期变形仍将继续增加,需加强滑坡变形的监测与控制。 3)本文仅对八字门滑坡的水平位移进行了变形趋势分析,在条件允许下,可进一步进行滑坡其他变形项目的类似研究,以便充分掌握八字门滑坡的变形规律。2 实例分析
2.1 工程概况


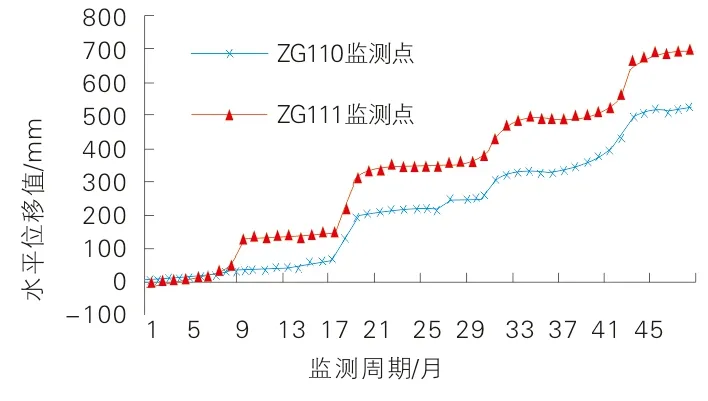
2.2 误差信息的剔除处理



2.3 水平位移变形趋势分析
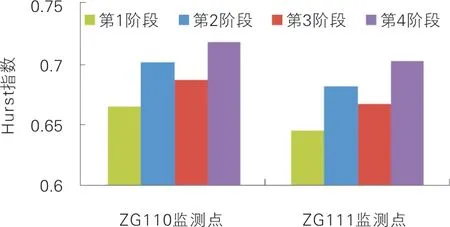
3 结论
