广义指数递减模型改进及其在油气田开发评价中的应用

陈元千 宋 珩 徐佳倩 孙银行 陈 松

（中国石油勘探开发研究院 北京 100083）

产量递减法的应用，不受储集类型、油气藏类型、驱动类型和开发方式的限制，只要油气田的生产已经进入递减阶段，即可有效地应用。由于指数递减简单易行，预测的指标比较稳妥可靠，因此，受到国际上市评估公司和油气开采公司的普遍采用。然而，由于指数递减的递减率为常数，产量的递减比双曲线递减和调和递减要快，因此，预测的产量和可采储量比双曲线递减和调和递减低。但实际应用表明，双曲线递减出现的概率较少，调和递减出现的概率很低，而指数递减出现的概率可达90%以上。Arps[1-2]提出的指数递减，主要用于无峰递减模式递减阶段的产量和累积产量的预测。陈元千[3]基于Arps的指数递减，于2005年提出了预测油气田可采储量和剩余可采储量的快速方法，此法于2010年被列于国家的行业标准[4]。此后，该法在评价井网加密调整效果[5-6]、评价注聚合物提高采收率效果[7]、评价重质油热力开采效果[8-9]、页岩气井控可采储量[10-11]和年度标定油气田开发指标[12]等方面，均取得了比较满意的效果。正基于此，陈元千[13]于2016年提出了广义递减模型。本文将着重分析广义指数递减在油气田开发指标预测方面的应用。

1 不同油气田开发模式的总累积产量

图1给出了4种油气田开发模式，即无峰开发模式（图1a）、单峰开发模式（图1b）、均峰开发模式（图1c）和多峰开发模式（图1d）。无峰开发模式，就是Arps（1945）提出的3种递减所遵循的开发模式。4种开发模式在产量递减阶段某时间的总累积产量可表示为

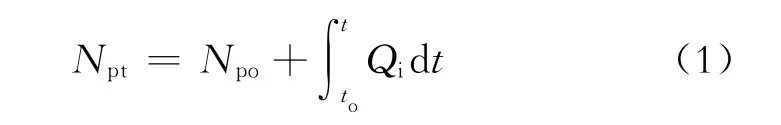
对于上述4种开发模式，Npt为从投产计量产量的总累积产量；Npo为从投产计量产量到to时间的累积产量；to为从投产时间到产量开始递减的时间；t为从投产时间到递减阶段的某时间；Qi为to时间的初始理论产量。应当指出的是，对于无峰开发模式，to=0和Npo=0。

2 广义指数递减预测公式的推导

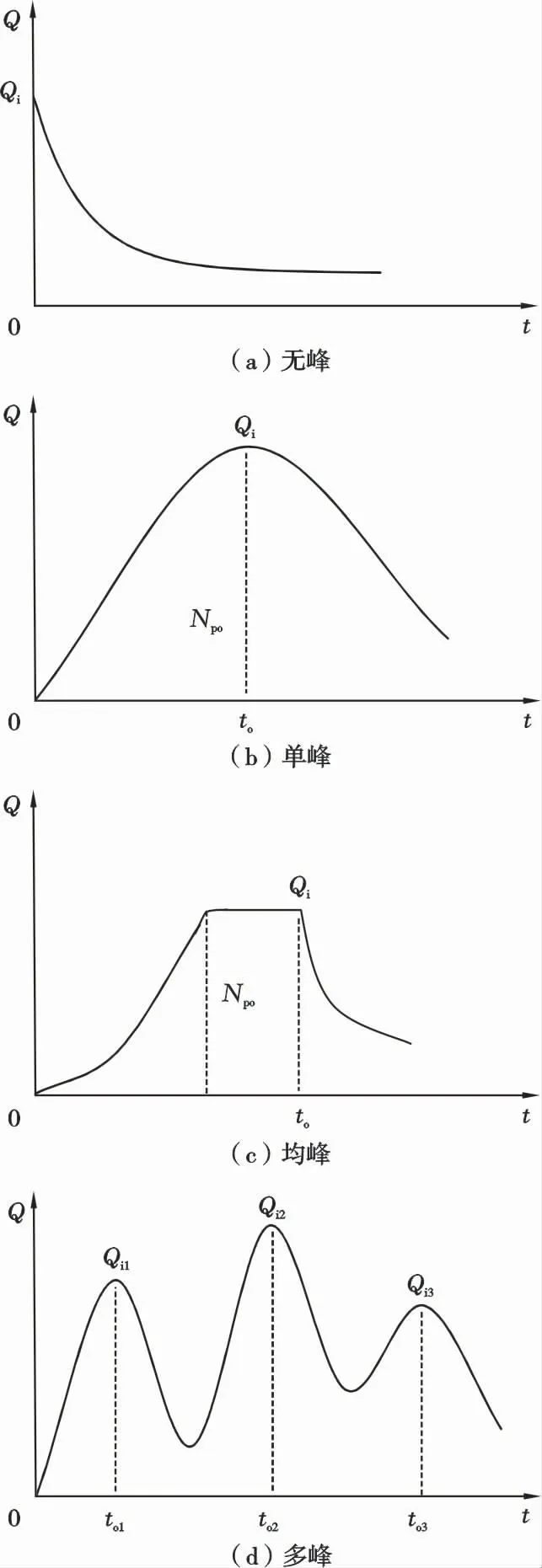
图1 油气田开发模式示意图Fig.1 Schematic diagram of the development modes of oil and gas fields

广义指数递减的主要预测公式，包括用于预测递减阶段的产量、总累积产量、经济可采储量、技术可采储量、剩余经济可采储量、剩余技术可采储量、经济可采储量的采出程度、技术可采储量的采出程度、剩余经济可采储量的储采比和剩余技术可采储量的储采比等。本文在文献[13]的基础上，经过推导得到了如下更为简单实用的预测方法。

预测油气田产量的公式为

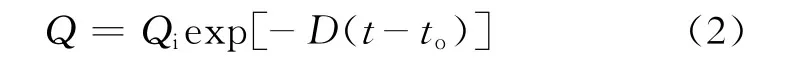
将式（2）代入式（1）经积分后可得，总累积产量与产量的关系式为

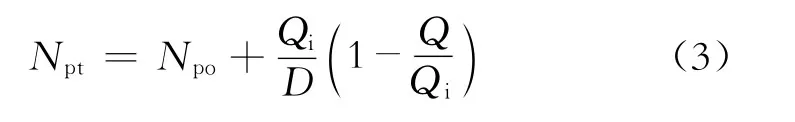
再将式（2）代入式（3）得，预测总累积产量的公式为

当Q=QEL（经济极限产量）时，由式（3）得经济可采储量的预测公式为

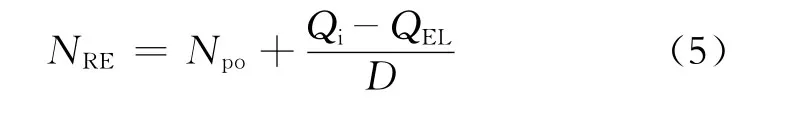
根据国家行业标准[4]的规定，当Q=0时，由式（3）可得预测技术可采储量的公式为

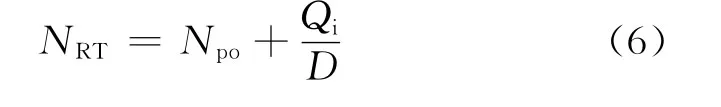
已知剩余可采储量表示为

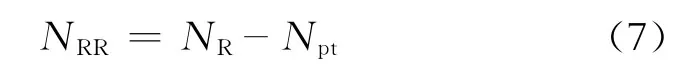
将式（4）和（5）代入式（7）得预测剩余经济可采储量的公式为

再将式（4）和式（6）代入式（7）得预测剩余技术可采储量的公式为：

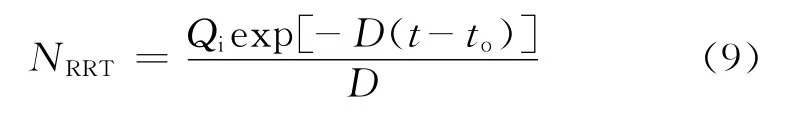
已知可采储量的采出程度表示为

将式（4）和（5）代入式（10）得预测经济可采储量采出程度的公式为

再将式（4）和式（6）代入式（10）得预测剩余技术可采储量采出程度的公式为

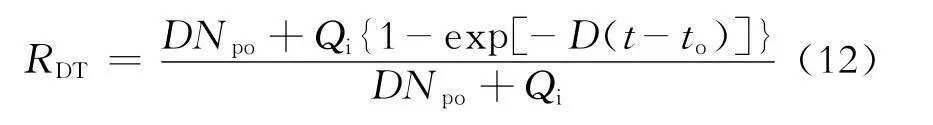
已知储采比的定义为某年的剩余可采储量与当年的年产量之比，即

将式（2）和式（8）代入式（13）得预测剩余经济可采储量的储采比公式为

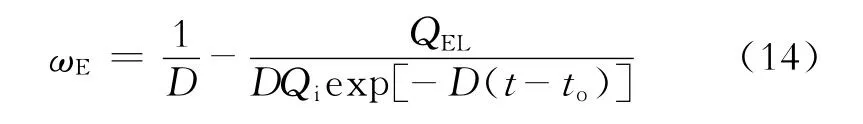
再将式（2）和（9）代入式（13）得预测剩余技术可采储量的储采比公式为

3 Qi和D两个常数确定的方法

由上述的预测公式可以看出，公式中都存在Qi和D两个常数，为求取这两个常数的数值，将式（3）改写为下式：

其中

由式（16）可以看出，对于广义指数递减，递减阶段的Q与Npt的相应数据绘于直角坐标上，将是一条下降的直线。由线性回归可求得直线的截距a、斜率b和相关系数的数值。由式（18）看出，直线的斜率b就是递减率D。再将式（17）改写为下式，可得确定递减阶段初始理论产量为

4 应用实例

中国境外合作开发的Zana油田，属于碳酸盐岩似层状微裂缝性水驱油藏，1994年进行人工注水，含油面积109.3 km2，由容积法评价的原始地质储量4.151×108t。该油田于1986年投产，进入产量递减阶段的时间to=23 a，此时的累积产量Npo=4 830×104t。由式（16）绘成的Q与Npt关系图，见图2所示。经线性回归求得直线的截距a=765.51、斜率b=0.071 6和相关系数r=0.992 3。将a、b和Npo的数值代入式（19）得，递减阶段开始时的初始理论产量为419.68×104t。

图2 Zana油田的Q与Npt关系图Fig.2 Relationship between Q and Npt of Zana oilfield

将Qi、D和Npo的数值，以及假定的经济极限年产量QEL=10×104t／a的数值代入式（5）得该油田的经济可采储量为NRE=104t=1.055 2×108t。

再将Npo、Qi和D的数值代入式（6）得该油田的技术可采储量为1.069 1×108t。

若将Qi、D、Npo、to和QEL的数值，分别代入式（2）、（4）、（8）、（9）、（11）、（12）、（14）和（15），预测该油田递减阶段的产量Q、总累积产量Npt、剩余经济可采储量NRRE、剩余技术可采储量NRRT、经济可采储量的采出程度RDE、技术可采储量的采出程度RDT、剩余经济可采储量储采比ωE和剩余技术可采储量储采比ωT等随时间的变化，见图3～7所示。由图3～4看出，预测的线和实际的数据点符合很好。再由图7看出，ωE随时间t有所减小，而ωT随时间为常数，等于14 a。已知递减率D=0.071 6 a-1，将其代入式（15）得

利用本文方法预测Zana油田不同重点年份的开发指标列于表1。

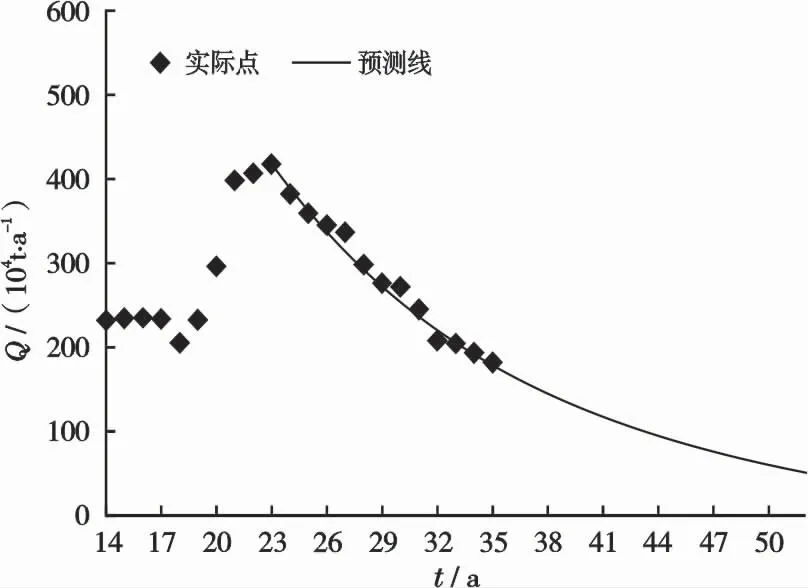
图3 Zana油田的Q与t关系图Fig.3 Relationship between Q and t of Zana oilfield

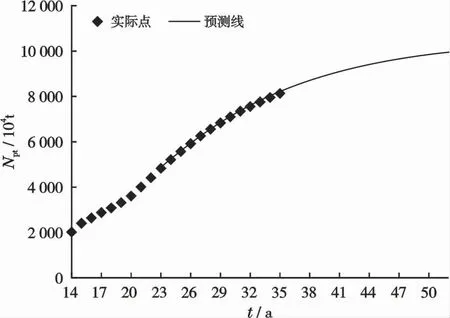
图4 Zana油田的Npt与t关系图Fig.4 Relationship between Npt and t of Zana oilfield

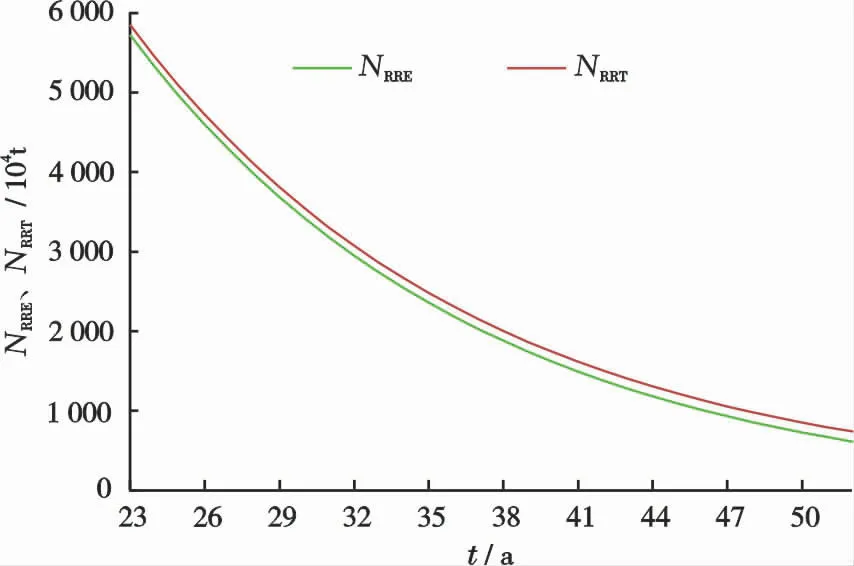
图5 Zana油田的NRRE和NRRT与t关系图Fig.5 Relationship between NRRE、NRRT and t of Zana oilfield

图6 Zana油田的RDE和RDT与t关系图Fig.6 Relationship between RDE、RDT and t of Zana oilfield

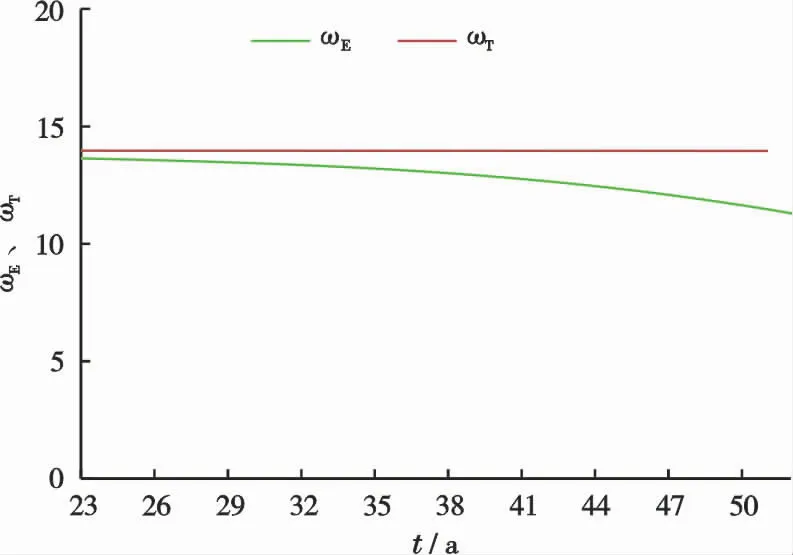
图7 Zana油田的ωE和ωT与t关系图Fig.7 Relationship betweenωE、ωT and t of Zana oilfield

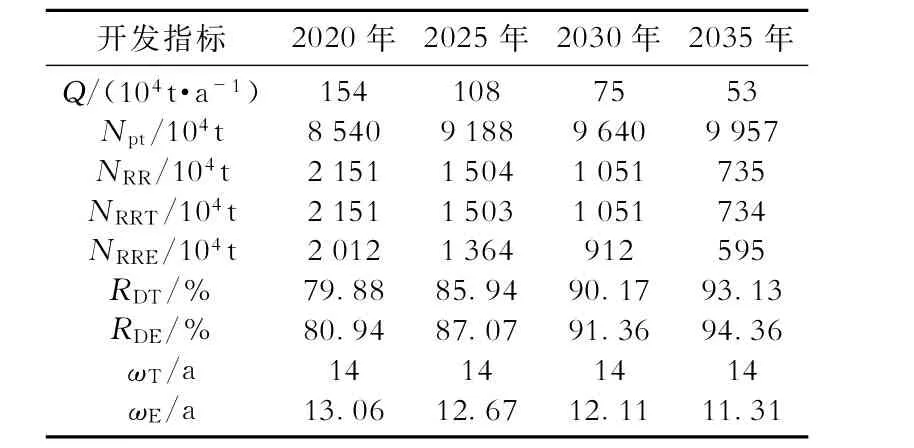
表1 Zana油田重点年份开发指标的预测结果Table1 Prediction results of different main years development indexs of Zana oilfield

5 结论

广义指数递减适用于无峰、单峰、均峰和多峰等开发模式。在产量进入递减阶段之后，广义指数递减用于预测油气田的产量、总累积产量、经济可采储量、技术可采储量、剩余经济可采储量、剩余技术可采储量、经济可采的采出程度、技术可采的采出程度、剩余经济可采储量储采比和剩余技术可采储采比等开发指标。通过Zana油田的实际应用表明，广义指数递减预测的理论线，同实际生产的数据点符合很好，不同重点年份预测的指标具有实际的参考价值。预测的采收率偏低的原因在于，评价碳酸盐岩储层的有效厚度和有效孔隙度评价的数值过高。当然，这两项参数是不用于准确评价的。

符号注释

Q—t时间的年产量，104t·a-1；

Qi—to时间初始理论年产量，104t·a-1；

D—年递减率，a-1；

t—从投产计时的生产时间，a；

to—油田进入产量递减阶段的生产时间，a；

Npt—递减阶段生产到t时间的总累积产量，104t；

Npo—从油田投产开始计时间到to时间的总累积产量，104t；

NR—可采储量，104t；

NRE—经济可采储量，104t；

NRT—技术可采储量，104t；

NRR—剩余可采储量，104t；

NRRE—剩余经济可采储量，104t；

NRRT—剩余技术可采储量，104t；

RD—可采储量的采出程度，f；

RDE—经济可采储量的采出程度，f；

RDT—技术可采储量的采出程度，f；

ω—剩余可采储量储采比，a；

ωE—剩余经济可采储量储采比，a；

ωT—剩余技术可采储量储采比，a；

a和b—递减阶段Q与Npt直线关系的截距及斜率。