新型射流振荡减摩阻工具设计及内部流场特性数值模拟分析与实验验证*

田家林 何虹志 杨 琳 杨应林 宫学成 胡志超 李居瑞

（1.西南石油大学机电工程学院 四川成都 610500； 2.中海油海洋石油工程（青岛）有限公司 山东青岛 266520）

在油气井实际钻井过程中，由于地层环境差异导致井下工况条件非常复杂，随着新型钻井技术的发展，各种新型钻井工艺不断被开发应用，导致钻柱与井壁之间的钻井摩阻影响因素呈现多样性，使井下工具安全评价、钻井过程减摩降阻与提速增效面临新的挑战[1-4]。越来越多的学者与研究机构也认识到该问题的重要性，经过不断探索研究，研制出不同类型的井下减摩降阻工具，应用于石油天然气勘探开发领域，以实现钻井过程中减摩降阻与提速增效[5-8]。

现有的减摩阻工具通常利用轴向冲击与周向冲击作用，将钻井液的液压能转变为工具的机械能，使工具产生振动，通过在钻具组合中加入减摩阻工具，能够有效降低钻井摩阻，提高钻进效率[9-10]。轴向减摩阻工具通过工具工作产生轴向振动，形成轴向冲击力，改变钻柱轴向受力条件，实现轴向振动减摩作用，相关工具有水力振荡器、防滞动工具、连续管减摩器等[11-14]；周向减摩阻工具产生的周期性扭矩传递到钻头，为钻头破岩提供一个额外的周期性扭矩，可提高钻头破岩效率，常见的周向工具为扭力冲击器[15]。但是常用的减摩阻工具存在结构复杂、耐冲蚀性能差、易受地层环境影响等缺点，限制了减摩阻工具的推广应用。

因此，为简化工具结构，提高工具使用寿命，笔者设计了一种射流振荡减摩阻工具，并结合该工具的工作原理，进行了射流短节内部流体流动特性研究，通过CFD-Post处理得到数值模拟结果，最后通过实验测试，验证了数值模拟结果的正确性。研究结果可为射流振荡减摩阻工具结构优化设计提供帮助，也可为进一步展开射流振荡减摩阻工具相关理论研究提供参考。

1 新型射流振荡减摩阻工具结构设计

新型射流振荡减摩阻工具由减震器和射流振荡器两部分组成，其具体结构如图1所示。射流振荡器安装在减震器前端，在射流振荡器内部设置射流短节。由于射流短节存在特定形状的射流腔，当钻井液进入射流振荡器后，通过在射流腔内循环，按照特定的循环路线完成循环后，从流体出口流出，形成钻井液工作压降。

图1 射流振荡减摩阻工具结构示意图Fig.1 Schematic diagram of jet oscillation friction reducing tool

当流体在射流短节内循环时，若首先形成向上的入射流，经过射流短节上部输入通道进入振荡室，产生顺时针涡流；当完成依附壁面转换后，流体经过下部输入通道进入振荡室，产生逆时针涡流，形成周期性的附壁与切换，形成流体的康达效应。在工作过程中，射流振荡器将产生周期性的脉冲压力波，并传递到射流振荡器后端的减震器上，在脉冲压力的作用下，减震器内部串联的碟簧组出现周期性地压缩与复位，使工具产生周期性的轴向振动，从而实现减摩阻作用。相对现有常用的水力振荡器、射流工具等减摩工具，本文提出的射流振荡减摩阻工具的射流振荡器内部无运动件，依靠流体在循环流道内自动切换产生射流振荡效果，从而实现减摩阻功能，而不是依靠运动部件的转动来改变流体的流动特性，因此结构更简单。

2 流场特性数值模拟分析

2.1 模型建立

2.1.1 几何模型建立

根据射流振荡减摩阻工具的结构设计，按照表1中的主要结构参数，建立射流短节内部流体计算域结构模型，结构模型包括入水管流域、上下控制端口流域、上下输入流道流域、上下直线流道流域、弯曲流道流域、振荡室流域与出入口流域等，如图2所示。

表1 射流短节主要结构参数Table1 Main structural parameters of jet joint

图2 射流短节内部流体计算域结构模型Fig.2 Computational domain structure model of fluid in jet joint

2.1.2 控制方程

射流振荡减摩阻工具以钻井液为输送介质，钻井液进入射流短节后，经过内部流道，射流振荡器产生振荡作用。忽略钻井液所受到的体积力，并且钻井液不与外界发生热交换。结合射流短节内流体的流动状态，选择RNGk-ε湍流模型，该模型由瞬时纳维-斯托克斯方程（N-S）演化而来，针对N-S方程进行时间平均后即可得到雷诺平均N-S方程[16]：

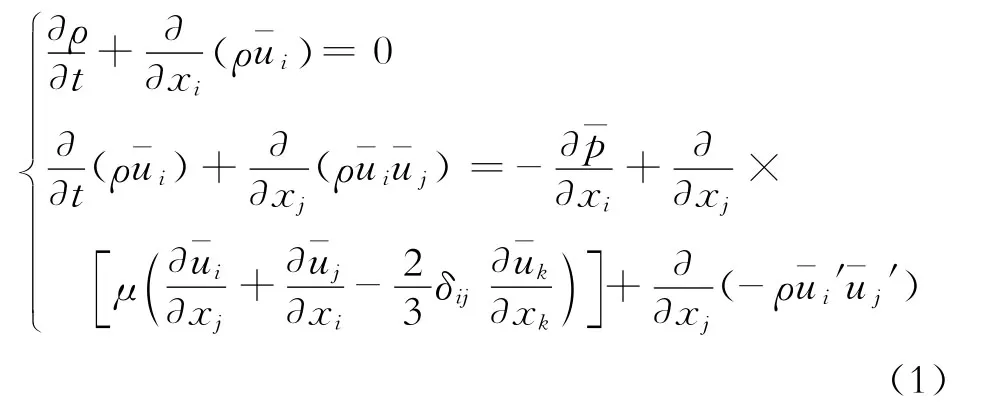
式（1）中：ρ为流体密度，kg／m3；t为时间，s；x i、x j、x k分别表示分量符号（i=1、2、3，j=1、2、3，k=1、2、3）分别表示雷诺平均速度分量，m／s；μ为动力黏度，N·s／m2¯p为平均压强，Pa′分别表示平均脉动流速分量，m／s；δij为克罗内克张量分量。

通过布西涅斯克假设，可以将雷诺应力与平均速度梯度相关联起来，其雷诺应力模型为[16]

其中

式（2）、（3）中：μt为湍流黏度，Pa·s；k为湍流动能，m2／s2；ε为湍流动能耗散率，m2／s3；C为经验常数，取C=0.09。

在RNGk-ε模型中，湍动能k和湍流动能耗散率ε分别由式（4）、（5）表示[17]

式（4）、（5）中：C1、C2为经验常数，取C1=1.44、C2=1.92；σk为湍流动能的普朗特数，取σk=1；σε为湍流动能耗散率的普朗特数，取σε=1.3。

2.1.3 定解条件

在同一网格模型中，改变入口流量大小（2、4、6、8和10 L／s）进行计算，得到射流振荡减摩阻工具工作时射流短节内流体部分参数的变化规律。在计算过程中，计算模型的入口定义为速度边界条件，出口定义为压力出口，出口压力定义为一个大气压。计算模型入口、出口湍流强度和水力直径可以通过式（6）计算得到[18]。

式（6）中：I为湍流强度，%；Re为雷诺数；Dh为水力直径，m；υ为流体流速，m／s；A为过流面积，m2；Cl为过流截面周长，m。

不同入口流量条件下的边界条件参数见表2。

表2 不同入口流量条件下的边界条件参数Table2 Boundary condition parameters under different inlet flow conditions

2.2 模拟计算结果分析

通过数值模拟计算，得到不同入口流量条件下射流振荡减摩阻工具射流短节内部流体工作参数，包括压力场、速度场等计算结果，并对不同位置的流体工作参数进行监测和分析，主要对流体入口、流体出口、分流中心点以及流体中心截面的参数变化进行监测，具体位置如图3所示。

2.2.1 速度场分析

结合数值计算过程，流体在射流短节内的流动存在附壁与切换现象，以入口流速为3.056 m／s的初始条件为例，整个附壁与切换过程中的流速变化如图4所示。由图4可以看出，在初始阶段，流体经过入水管直线流道进入扩散段后，首先完成均匀射流，随着时间的增加，流体开始沿着上部输入通道进行切换，直到大部分流体依附于上部输入通道；然后进行中间切换，再逐渐依附于下部输入通道，完成流体在射流短节内的附壁切换过程。从模拟过程可以看出，射流振荡器工作正常，流体在射流短节内能够顺利完成附壁与切换过程。

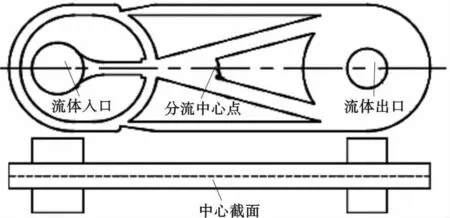
图3 模拟监测界面位置示意图Fig.3 Schematic diagram of simulation monitoring interface location

图4 射流振荡减摩阻工具模拟过程（入口流速为3.056 m／s）Fig.4 Simulation process of jet oscillation friction reducing tool（inlet velocity is 3.056 m／s）

通过建立监测截面，分别得到不同初始条件下射流短节内部流体中心截面上的速度分布云图。通过CFD-Post得到不同入口流速条件下的x-y平面内的速度计算结果，如图5所示。从图5可以看出，当流速较低时，流体进入射流短节后在振荡室内做无规律运动，大部分流体通过流体出口流出，较少部分流体通过上下直线流道回流至弯曲流道（图5a）；当流体入口流速增加到一定数值大小后，流体在振荡室内形成规则的旋流，在上下直线流道内不存在回流（图5d）；当流体入口流速继续增大，振荡室内流体的旋流状态变紊乱，上下直线流道内再次出现回流现象（图5f）。

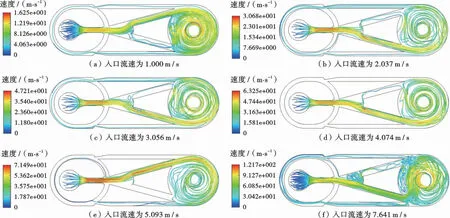
图5 不同入口流速下的速度计算结果Fig.5 Results of velocity calculation at different inlet velocities

2.2.2 压力场分析

通过速度场分析，完成了射流短节内部流体的流动状态研究，使流体在射流短节内的循环路线得到验证，为进一步开展射流振荡减摩阻工具内部流场研究，进行射流短节内流体的压力场分析，得到不同入口流速下的压力场计算结果，如图6所示。

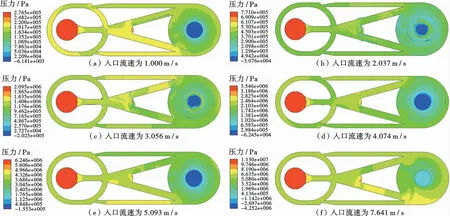
图6 不同入口流速下的压力计算结果Fig.6 Pressure calculation results at different inlet flow rates

由图6可以看出，流体入口位置压力最大，随着流体在射流短节内循环，流体压力逐渐降低，在流体出口位置，流体压力最低；在上下输入通道位置压力分布差异比较明显，在流体流速更大位置压力反而相对更低，这是由于流体在射流短节内存在附壁切换现象；在上下直线流道和控制端口位置，流体压力也与流体流速分布规律相反；流体经过入水管流道和扩散段后，由于与分流劈之间存在水力冲击作用，在分流中心点处压力大小明显高于附近位置的压力。

2.2.3 分流中心点压力分析

结合压力场分析结果，分析分流中心点的压力变化，得到不同入口流量条件下分流中心点的压力变化曲线，结果如图7所示，其中在数值计算过程中，计算时间步均为5 000步，每一步时长为0.01 s。

图7 不同入口流速条件下，分流中心点压力变化曲线Fig.7 Pressure change curve of the shunt center point under different inlet velocity conditions

由图7可以看出，随着入口流量增大，即入口流速增加，分流中心点处压力逐渐增大；随着计算时间的增加，一段时间后模拟的6种入口流量条件下的分流中心点压力均出现周期性压力波动，与模拟得到的附壁切换现象保持一致；不同入口流速条件下，当流体在射流短节内均匀射流时分流中心点压力波动范围与压力值相对较小，当流体在射流短节内产生附壁切换现象后，分流中心点位置的压力开始出现周期性波动，但周期性压力波动平稳后，其周期均保持在10 s左右。

3 实验验证

为了分析研究仿真分析结果的准确性，按照设计参数加工了一套射流振荡减摩阻工具进行实验测试，其中射流短节如图8所示。实验方案如图9所示，射流振荡减摩阻工具以水平方式放置，采用一端固定一端轴向游动，将减震器端使用机械机构进行夹持，保证左端不产生轴向移动，射流振荡器端游动。采用双泵系统对测试工具进行供液，泵1和泵2从水箱中吸水，经过出口总阀、入水软管进入射流振荡减摩阻工具，由右端流出，经过出水管流回水箱。实验过程中，所用的流体介质均为清水，通过流量压力监测控制台实现流量与压力的监测与调节。

结合实验测试方案进行实验测试，实验现场如图10所示。每次调节泵输入流量后，待射流振荡减摩阻工具工作平稳后，通过数据采集仪器进行压力数据采集。

图8 新型射流振荡减摩阻工具射流短节Fig.8 Jet joint of the new jet oscillation friction reducing tool

图9 测试设备安装方案示意图Fig.9 Schematic diagram of test equipment installation scheme

图10 射流振荡减摩阻工具实验现场Fig.10 Jet oscillation friction reducing tool test site

将压力测试结果与数值模拟计算结果进行对比，得到实验测试结果与仿真计算结果对比图，如图11所示。由图11可以看出，实验测试结果与仿真计算结果得到的压力参数与入口流速之间的变化规律基本一致。在射流振荡减摩阻工具工作过程中，随着入口流量的增加，射流振荡减摩阻工具的入口压力与出口压力均逐渐增加，出口压力大小增加缓慢，而入口压力增加速度较快，测试压降变化规律与入口压力变化规律保持一致。但实验测试得到的压力参数大小低于数值模拟得到的压力参数，其原因在于实验测试过程中，压力测试点为测试管线进出口位置，而数值模拟计算结果的压力参数对应于射流短节流体出入口位置，并且在测试过程中，测试管线存在一定的漏失，都将导致测试结果低于数值模拟计算结果。

图11 实验测试结果与仿真结果对比Fig.11 Comparison of experimental test results and simulation results

在其他条件不变的情况下，依次改变泵的输入流量，测试不同流量下工具的频振动率与加速度，测试现场如图12所示，测试结果见表3。从表3测试结果可以看出，随着入口流量增大，工具的振动频率变快，振动幅度变大。

图12 射流振荡减摩阻工具振动测试Fig.12 Vibration test of jet oscillation friction reducing tool

表3 不同流量条件下的振动测试结果Table3 Vibration test results under different flow conditions

4 结论

1）针对现有钻井工艺中井下减摩阻工具结构复杂、工作过程易受地层环境影响等问题，设计了一种新型射流振荡减摩阻工具，该工具通过射流短节内产生的工作压降，形成脉冲压力波，作用在减震器上产生轴向振动，以改变钻柱受力状态，降低钻井摩阻。新型射流振荡减摩阻工具的射流振荡器内部无运动件，结构更加简单，依靠流体在循环流道内自动切换产生射流振荡效果，实现减摩阻功能。

2）数值模拟分析和实验研究结果表明，本文设计的新型射流振荡减摩阻工具内部流场随着入口流量的增加，入口压力与出口压力均逐渐增加，出口压力增加缓慢，入口压力增加速度则较快；实验测试压降变化规律与入口压力变化规律保持一致，验证了射流振荡减摩阻工具结构设计的合理性和可靠性，可为实现射流振荡减摩阻工具的现场实际应用提供参考。