一种求解等效旋转矢量高阶误差补偿系数的新方法

严恭敏，李思锦，郭正东

（1.西北工业大学 自动化学院，西安 710072；2.海军潜艇学院，青岛 266199）

捷联惯导算法的关键在于姿态更新算法，其主流方法是先使用陀螺角增量多子样采样计算等效旋转矢量，补偿转动不可交换误差，再使用等效旋转矢量计算姿态更新四元数。等效旋转矢量多子样算法的理论基础是Bortz 方程[1]，传统基于泰勒级数展开或基于圆锥运动环境下优化的多子样算法推导，都忽略了Bortz方程中三阶以上项的影响，虽然理论上在一个姿态更新周期内子样数越多精度越高，但是，实际算法精度往往达不到宣称的理想效果，特别是在大角度机动或大锥角圆锥运动环境下，有时采用高子样算法的精度反而不如低子样算法的精度。

目前，提高姿态解算精度的研究方向主要有两个。其一是数值迭代算法，姿态的数学表示方法有姿态阵、等效旋转矢量、四元数和罗德里格参数等，只要能建立起这些表示方法与角速度输入之间的运动学关系，均可以采用积分或微分数值迭代计算的方法进行求解，这类方法的优点是精度高且实现简单，稍显不足之处是计算量略大[2-6]。其二是等效旋转矢量的高阶误差补偿算法，它考虑了Bortz 方程中高阶项的影响，将高阶项表示为多子样的多重叉积之和的形式，先推导求解出高阶误差补偿系数再进行补偿，其优点是在进行姿态更新应用时计算量相对较小[7]。

等效旋转矢量高阶误差补偿系数的求解是比较烦琐的，但幸运的是可以将Bortz 方程中的低阶项分解为多个部分，各部分恰好能够表示为不同重数的叉积形式，且它们之间互不相关，只要分别进行求解即可[7,8]。文献[9]给出了单重叉积系数即传统多子样系数的随机仿真求解算法，通用性强且计算机编程实现简单；文献[10]借鉴同样的思路，给出了双重叉积和三重叉积系数的求解算法，但由于多重叉积之间存在相关性问题，去除相关过程的推导依然有些烦琐。本文采用多重叉积矩阵秩的数值判断方法直接消除相关性，更加简单，该方法可直接推广至五子样和六子样等更高子样算法。最后，在圆锥运动和大机动情况下进行了算法的对比仿真验证，并给出了一些实际使用建议。

1 高阶误差补偿算法原理

等效旋转矢量微分方程(Bortz 方程)为[1]

其中，ω为动坐标系相对于参考坐标系的转动角速度输入，为等效旋转矢量φ的模值。将式(1)中的余切函数作泰勒级数展开，经整理后可得

将等效旋转矢量作如下“和分解”[7]

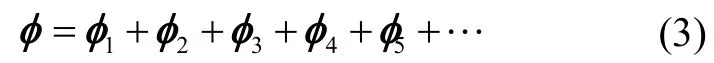
再将式(3)代入式(2)，可得

令式(4)左右两边的项一一对应相等，可得如下五个子式

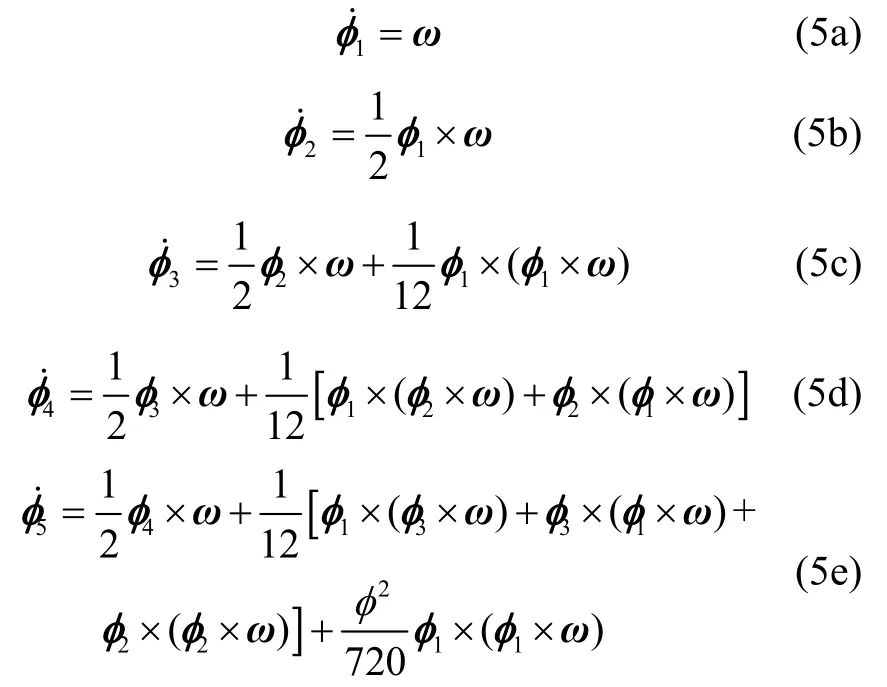
假设输入角速度ω为关于时间t的(N- 1)次多项式，即

式中，wj(j=N- 1,N- 2… 0)均为三维列向量，W为3×N维的系数矩阵。假设在一个姿态更新时间段（0,T］内进行了N次等间隔陀螺角增量采样，记为Δθj+1，显然有

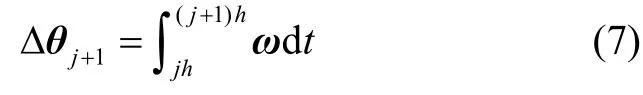
式中，h=T/N为陀螺采样间隔。根据文献[9]，有角速度多项式系数与角增量之间的关系

式中，Γ是与N和T有关的已知矩阵。由式(8)可知，角速度多项式各项系数wj均是所有角增量采样Δθj+1的线性组合，因此式(6)中角速度ω总可以表示为角增量 Δθj+1的线性组合多项式形式，即

式中，γij为逆阵Γ-1的第i行j列元素，是已知量。式(5a)显示，φ1是角速度ω的积分即角增量，因而φ1也可以表示为Δθj+1的线性组合多项式形式，根据式(9)可得

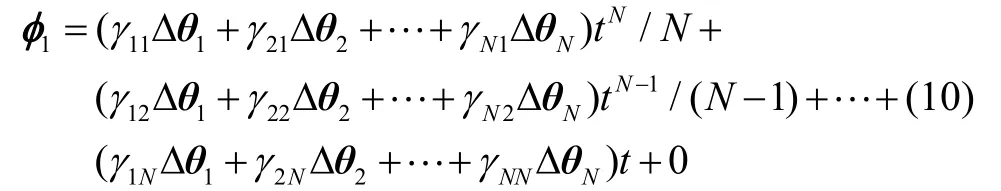
若角速度ω关于时间t的最低非零幂次为0、最高非零幂次为N- 1，则经积分后，角增量φ1的最低非零幂次为1、最高非零幂次为N；考虑到ω和φ1的最低非零幂次项和最高非零幂次项是线性相关的，则在一般非定轴转动情形下叉积φ1×ω的最低非零幂次为2、最高非零幂次为2N- 2，所以式(5b)经积分后φ2的最低非零幂次为3、最高非零幂次为2N- 1；以此类推，可分析得φ3、φ4和φ5等分解项的最低和最高非零幂次，总结见表1。其中，在式(5e)的右端最后一项中含等效旋转矢量模方因子φ2，显然φ2=φTφ的最低非零幂次为2、最高幂次为无穷，所以φ5的最高非零幂次是无穷的。

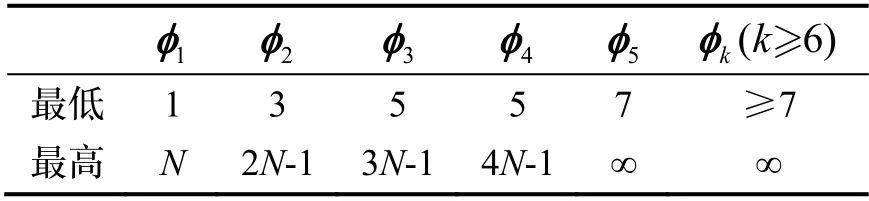
表1 等效旋转矢量分解的最低和最高非零幂次Tab1.The lowest and highest non-zero power for the decomposition of rotation vector

根据三维向量的叉乘性质，将式(10)叉乘式(9)，其结果必定可以表示成如下N(N- 1)/2项单重叉积的线性组合形式

式(11)中，ki′j是与γij和时间t有关的系数，具体表达式比较复杂。将式(11)对时间积分不会改变其整体表示形式，仅会改变系数ki′j，因此，由式(5b)可知φ2也总可以表示为角增量采样单重叉积 Δθi×Δθj的线性组合形式，记为

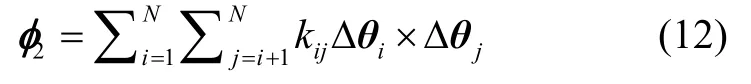
依此类推，φ3可以表示为N2(N- 1)/2项双重叉积 Δθi×(Δθj×Δθk)的线性组合；而φ4也可以表示为N3(N- 1)/2项三重叉积的线性组合（注意:在文献[7,10]中将φ4分为φ4-1和φ4-2两部分是没必要的，因为总有Δθj×［Δθi×(Δθk×Δθl)］成立，即φ4-2必定可以表示成φ4-1的线性组合）。然而，由于式(5e)中含因子φ2，理论上φ5不能完全表示为四重叉积形式，所以采用多子样多重叉积法最多只能精确补偿至三重叉积项。当然，若作模方近似φ2=(φ1+φ2+ …)T(φ1+φ2+ …)≈φ1Tφ1，则φ5的最高幂次为5N- 1，就有可能采用非叉乘的方式对其进行近似补偿，这不在论文的讨论范围内。

式(5)和表1表明，传统的等效旋转矢量误差补偿算法只补偿至φ2项，即忽略了φ3及其之后所有项，误差阶为O(t5)；φ3和φ4具有相同的误差阶O(t5)，若仅补偿φ3则误差依然为O(t5)，意义不大；若同时补偿φ3和φ4而忽略φ5，则误差阶为O(t7)。目前，所谓的高阶误差补偿算法，即为对φ2、φ3和φ4同时进行了误差补偿的等效旋转矢量多子样算法。

2 高阶误差补偿系数求解

2.1 求解步骤

根据式(9)和式(10)的表达方式直接求解式(12)中的单重叉积系数kij，甚至进一步求解双重或三重叉积系数，十分的烦琐。因此，这里通过随机数值仿真的方法求解这些系数，主要以求解双重叉积系数kijk为例，单重叉积系数kij和三重叉积系数kijkl的求解过程类似。

求解等效旋转矢量误差补偿双重叉积系数kijk的具体步骤如下:

（1）给定子样数N，不妨将等效旋转矢量更新周期作归一化处理，即令T=1；

（2）随机生成一组角速度多项式系数［wN-1wN-2…w0］，根据式(5a)～式(5c)和卷积算法[4]依次计算φ1、φ2和φ3的多项式系数，再计算多项式在T=1时刻取值φ3(1)，此即三阶不可交换误差的期望值。

（3）根据步骤（2）中的角速度多项式系数，按式(7)生成一组角增量数据［Δθ1Δθ2… ΔθN］，它们满足量测方程kijk为n=N2(N-1)/2个候选的待定系数；

（4）重复步骤（2）和（3）共记m次，一般需满足3m≥n，将所有量测方程合并在一起写成方程组形式

（5）根据向量的双重叉积性质（雅可比恒等式）V1×(V2×V3)+V2×(V3×V1)+V3×(V1×V2)=0可知，由角增量构造的矩阵不是列满秩的，可试着删去某一列并判断删除前后的秩是否一致，若相等则将该列删去并删去与该列对应的系数kijk，消除相关性，用此方法直到将角增量矩阵化为列满秩的，当然，也可通过调用Matlab 软件的“rref”函数获得角增量矩阵的极大无关列向量组直接实现列满秩。

（6）在角增量矩阵列满秩情况下利用最小二乘法求解方程组，得到n′个互不相关的双重叉积补偿系数kijk，可用Matlab 的“format rat”命令将浮点小数解转化为分数解输出。

2.2 二子样误差补偿系数

经过仿真计算，获得二子样算法的所有误差补偿系数如表2所列。

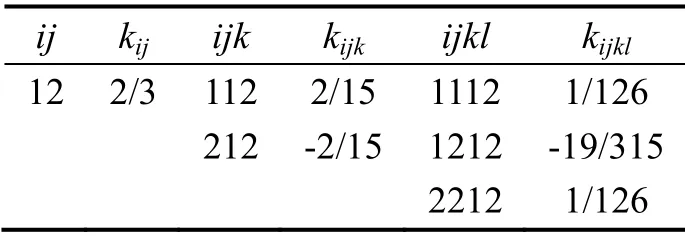
表2 二子样算法误差补偿系数Tab.2 Error compensation coefficients of 2 sub-sample algorithm

二子样算法的误差补偿系数数目不多，可根据表2直接写出完整的等效旋转矢量高阶误差补偿算法公式，为

式中，求和符号∑的右下标ij、ijk或ijkl表示遍历表2中的所有取值。后文三子样和四子样算法的误差补偿系数使用方法同式(13)，不再详细给出公式。

2.3 三子样误差补偿系数

三子样算法的误差补偿系数数目较多，参见表3，其中包含单重叉积系数3 个、双重叉积系数8 个、三重叉积系数18 个。

2.4 四子样误差补偿系数

四子样算法的误差补偿系数如表4和表5所列，共包含单重叉积系数6 个、双重叉积系数20 个、三重叉积系数60 个。

结果显示，表3和表4中的单重叉积误差补偿系数kij与文献[9]一致，它们都是在多项式角运动条件下获得的。文献[11]综合考虑了多项式角运动和圆锥运动的影响，推导并给出了所谓的扩展圆锥算法（见表3和表4第2 列括号内的数据），使其更加适应于圆锥运动环境。

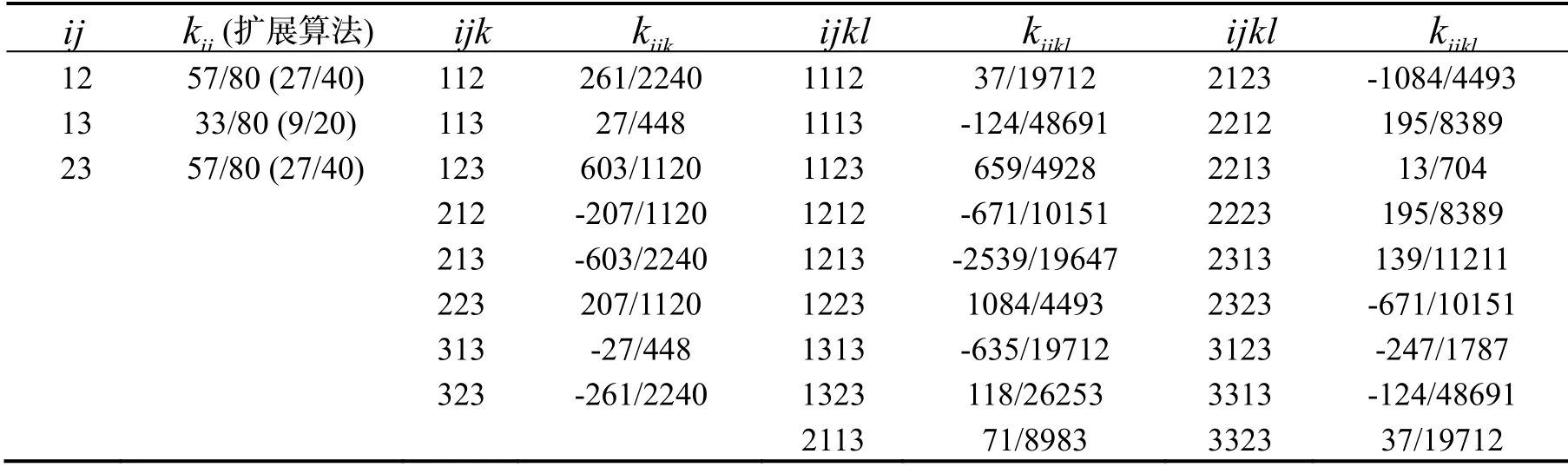
表3 三子样算法误差补偿系数Tab.3 Error compensation coefficients of 3 sub-sample algorithm

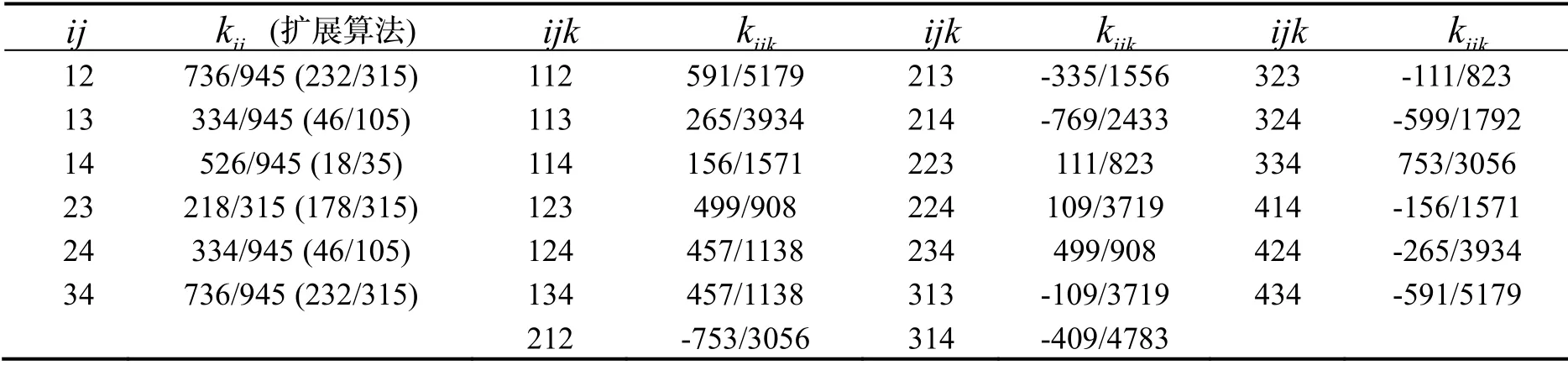
表4 四子样算法误差补偿系数（单重和双重叉积）Tab.4 Error compensation coefficients of 4 sub-sample algorithm (for single ＆ double cross product)

表5 四子样算法误差补偿系数（三重叉积）Tab.5 Error compensation coefficients of 4 sub-sample algorithm (for triple cross product)

表4中的双重叉积和表5中的三重叉积误差补偿系数与文献[7,10]的结果不完全一致，但系数的数目是对应相等的。究其原因主要在于本文采用2.1 节步骤（5）的方法消除角增量叉积之间的相关性，两种方法消去的系数不一样。本文方法无需细致的公式推导整理，直接利用计算机从数值上进行化简更加便捷。需要指出的是，在求解双重叉积和三重叉积等高阶误差补偿系数时，所有文献均未考虑圆锥运动的影响，因而，即使采用了单重叉积扩展圆锥算法，高阶误差补偿算法依然不能适应剧烈的高频大锥角圆锥运动环境。当然，要同时考虑多项式角运动和圆锥运动的影响，进一步推导高阶扩展算法是十分困难的。

利用本文方法还可以方便地求解五子样和六子样等更高子样数的算法，但误差补偿系数繁多且实际应用意义也不大，不再详细列出。

3 仿真验证

3.1 圆锥运动仿真

圆锥运动仿真参数设置为:圆锥频率f=2 Hz，半锥角变化范围α=0.01 °～90 °，角增量采样间隔h=10 ms。经过仿真，在圆锥轴上的姿态漂移误差ε如图1所示，图中实线为四元数迭代算法（Qpicard[2]）的姿态漂移误差，短虚线为扩展算法（Uncompressed[11]）的误差，点划线为“扩展+高阶误差补偿”算法（Uncomp+Highorder[7,10]）的误差，长虚线为本文给出的“非扩展+高阶误差补偿”算法（Comp+Highorder）的误差，四种算法均采用了四子样进行解算。从图1中可以看出:（1）当锥角较小时Uncompressed 算法是比较有效的，在锥角中等大小情况下须与Highorder 算法结合才具备更高的精度（提高约两个数量级），但当锥角很大时误差较Qpicard 大；（2）Qpicard 算法在全锥角范围内精度适中，当锥角很大时依然保持较高精度；（3）Comp+Highorder 算法在锥角不大的情况下精度与Qpicard 算法一致，而当锥角很大时与Uncomp+Highorder 算法几乎一样，精度均优于Uncompressed 算法。

图1 圆锥漂移误差对比Fig.1 Comparisons for coning drift errors

3.2 大角度机动仿真

这里选用文献[2,11]中的以多项式表示的2 s 大角度机动环境，重写多项式系数矩阵如下

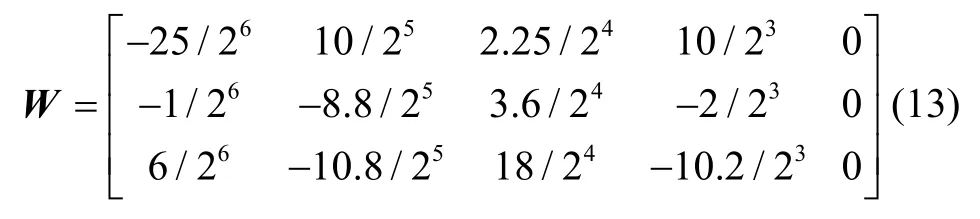
对Qpicard、Uncompressed、Uncomp+Highorder和Comp+Highorder 四种算法进行了仿真，采样间隔10 ms 且均为四子样算法，结果如图2所示。从图2中可以看出:（1）仅用Uncompressed 算法精度不高；（2）Qpicard 算法精度最高，说明特别适用于大角度机动情形；（3）Uncomp+Highorder 和Comp+Highorder两种算法的精度相当，可见在采用高阶补偿算法之后，与是否再运用扩展算法关系不大；（4）Highorder 算法与传统Uncompressed 算法相比精度提高了三个数量级。

图2 大机动失准角误差对比Fig.2 Misalignment angle comparisons under high-maneuvering

3.3 子样数与采样间隔关系仿真

圆锥运动条件同3.1 节，比较了四子样“扩展+高阶误差补偿”算法（Uncomp+Highorder4）与二子样高阶误差补偿算法（Highorder2）的差别，其中Uncomp+Highorder4 的采样间隔为10 ms、Highorder2的采样间隔为10 ms 并不断减半直至0.625 ms，仿真结果见图3。由图3可见，Highorder2 算法随着采样间隔的不断减小精度不断提高，且精度提高程度不受锥角大小的影响，采样间隔减半精度大约能够提高一个数量级，因此，选用高频低子样数的误差补偿算法往往比采用低频高子样数的算法更加有效。

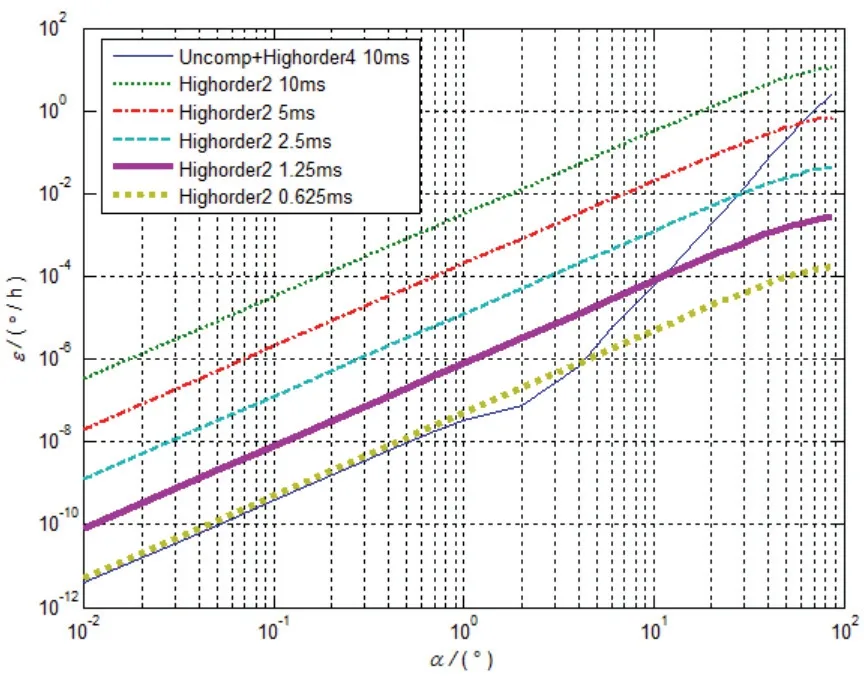
图3 不同子样数与采用间隔下的算法漂移Fig.3 Error drifts for different sub-sample number vs sampling interval

4 结 论

在捷联惯导系统姿态更新中，采用高阶误差补偿算法是提高等效旋转矢量解算精度一种措施，但是高阶误差系数的求解比较烦琐，文献[7]依靠解析推导的方法进行求解就出现了一处错误（参见文献[7]的表1中的系数a34-1，其值-238/5885 应为-101/1874），它很难依靠公式推导发现和复核。文献[10]应用更简单的随机仿真方法修正了该处错误，最终获得了全面正确的等效旋转矢量高阶误差补偿算法。本文同样也采用随机仿真的方法求解高阶误差补偿系数，但在消除误差补偿系数间的相关性时使用矩阵秩的数值判断方法，结果更加简洁，从根本上省去了公式推导的麻烦，具有更好的通用性和可推广性。

仿真表明，针对圆锥运动环境，“扩展+高阶误差补偿”算法在锥角不是特别大的情况下精度较高；而针对多项式大角度机动环境，迭代算法的精度更高。其实，不论哪种角运动环境，提高采样频率都可以大幅度地降低姿态更新误差，采用高频低子样数的简单算法远比采用低频高子样数的高阶误差补偿复杂算法更加有效。在实际应用中，由于受陀螺仪噪声误差等因素的制约，物理传感器造成的误差可能远比数学算法引起的误差大得多，因而选用过高精度的姿态更新算法没有太多实际意义，研究高精度迭代算法和高阶误差补偿算法更多的是理论参考价值。