不同速度列车脱轨撞击盾构隧道的动力损伤特性

2020-10-17孙明辉晏启祥李彬嘉吴政隆张建辉邓志鑫

中国铁道科学 2020年5期

孙明辉，晏启祥，李彬嘉，吴政隆，张建辉，邓志鑫

（1.西南交通大学交通隧道工程教育部重点实验室，四川成都 610031；2.中国水利水电第七工程局有限公司，四川成都 610081；3.四川省机场集团有限公司，四川成都 610042）

营运列车脱轨事故在世界范围内时有发生。2013年7月24日，西班牙1列快速列车由马德里开往费罗尔的途中发生严重脱轨事故；2016年11月20日，印度1 列14 节编组的快速列车全部脱轨；2019年9月12日，刚果民主共和国东南部坦噶尼喀省（Tanganyika）发生1 起列车脱轨事故；2020年2月6日，意大利1 列由米兰始发的高速列车在行驶途中脱轨造成人员伤亡。这些脱轨事故带来的惨痛教训至今仍尤为深刻。当前世界范围内铁路规模不断增长，铁路运营速度持续提高，一旦发生脱轨事故，造成的人员伤亡、财产损失等将更为严重。列车脱轨引发安全事故的潜在风险，正日益引起国内外学者的关注。在日本，学者Doi、Hung、Ishida、Sato 等建立了多体动力学模型，针对车辆的动态脱轨行为开展了一系列相关研究［1-4］。在我国，关庆华［5］对列车脱轨机理及运行安全性进行了系统研究；刘艳辉等［6］对欧洲规范中列车脱轨撞击结构设计进行了详细介绍；朱翔等［7］采用非线性有限元方法，分析了列车脱轨后的运行姿态；张景峰等［8］对脱轨列车撞击U 型梁的动态过程进行了仿真分析。但以上研究大多关注列车脱轨机理或是脱轨撞击地面结构物的动力响应。

近年来，开始有学者关注列车脱轨撞击盾构隧道相关动力响应问题。盾构隧道具有修筑速度快、对环境影响小等诸多优点，正逐渐成为修建城市地铁和铁路水下线路的首选方案。但同时，盾构隧道也存在整体刚度低、稳定性较整体式现浇衬砌结构差等缺点。当列车在隧道内脱轨时，势必会与隧道发生剧烈撞击，特别是在盾构隧道，因脱轨产生的撞击，极易引发衬砌结构损伤，严重时可导致盾构隧道贯穿性破坏、防水失效、局部结构失稳等一系列安全问题。对于此，张蒙［9］通过建立列车—刚性墙数值模型研究了盾构隧道衬砌动力响应特性；李彬［10］研究了撞击荷载下双层衬砌盾构隧道以及接头螺栓的开裂行为；晏启祥等［11-15］在总结前人研究的基础上，对列车撞击盾构隧道的动力响应进行了系统研究；肖明清等［16］研究了不同类型列车撞击盾构隧道的动力响应。以上研究采用的模拟方法，大多是提取列车撞击刚性墙仿真实验获得的撞击荷载，然后以平均面力的形式施加到盾构隧道内表面，没有考虑撞击过程中，列车与衬砌结构的非线性动态接触行为，更鲜有考察列车不同脱轨速度撞击盾构隧道衬砌管片损伤特性的相关研究。

为此，本文建立了考虑列车与盾构隧道非线性动态接触行为的有限元模型，依托上海—南通跨黄浦江盾构隧道工程，研究列车不同速度脱轨撞击作用下撞击荷载特性。基于混凝土塑性损伤理论，以200 km·h-1脱轨速度撞击下的盾构隧道为例，研究分析列车撞击下隧道管片衬砌的损伤演化规律，并对比研究列车不同脱轨速度撞击对衬砌管片拉压损伤的影响。以期解决前述问题，为盾构隧道的防撞设计提供参考。

1 考虑列车与盾构隧道非线性动态接触行为的有限元模型

为进行列车撞击盾构隧道动态过程的仿真分析，依托上海—南通跨黄浦江盾构隧道工程，分别建立围岩—衬砌模型和简化动车组列车模型。通过设置衬砌与列车之间的接触算法，对撞击过程进行仿真模拟。

1.1 围岩—衬砌模型

根据地质资料，选取隧道位于砂性土以及风化泥质粉砂地层当中。隧道衬砌内外直径分别为9.8和10.8 m，管片幅宽为2 m。衬砌管片采用错缝拼装方式，衬砌环接缝连接包括24 颗环向螺栓和22颗纵向螺栓。在保证计算精度的前提下，为了提高计算效率，仅将列车初始撞击位置附近的5环管片进行拼装式建模，并采用较小的网格尺寸；其余各环管片衬砌按照抗弯刚度等效的原则作均质化近似处理。

选取隧道的围岩—衬砌模型如图1所示，围岩模型的长、宽、高分别设置为120，40和40 m，上边界设置为自由边界，其余边界通过设置黏弹性人工边界来近似模拟岩体无限域边界条件。围岩和管片衬砌单元类型皆为8 节点缩减积分实体单元（C3D8R）。围岩单元数16 240 个，管片衬砌单元数127 584 个。围岩材料采用弹性模型，管片衬砌采用混凝土塑性损伤模型［18］。围岩、衬砌和接头螺栓的材料参数见表1。

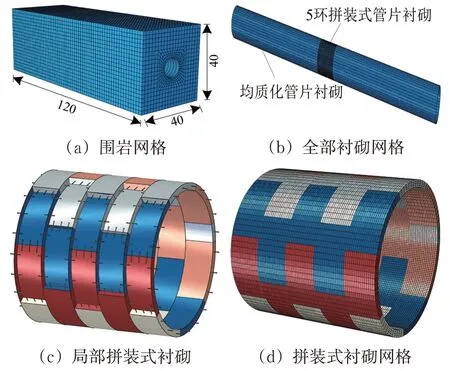
图1 围岩—衬砌有限元模型（单位：m）

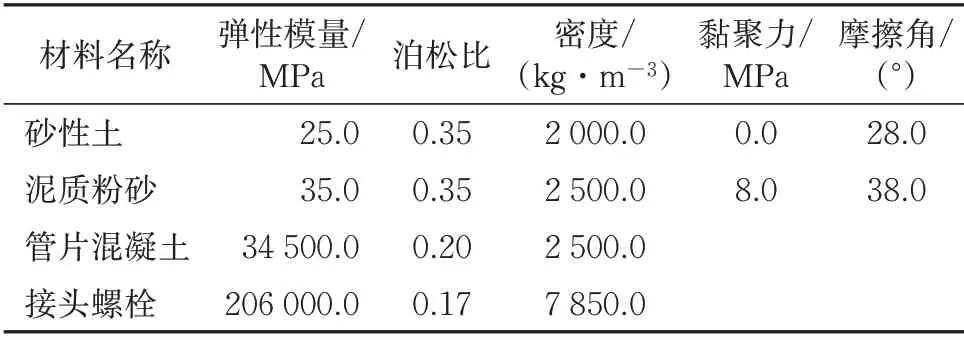
表1 材料参数

1.2 动车组列车简化模型

在列车高速撞击过程中，撞击荷载特征主要由前几节列车决定。英国学者Lu［17］研究发现，当列车编组辆数达到4节时，就与完全模拟整列编组列车获得的荷载具有较高的相似度。考虑到计算成本，本文在研究时，参照上述研究结果，建立4节编组的列车模型，进行撞击动态过程仿真分析。

依据实际列车尺寸，建立能反映列车基本几何特性的列车简化模型如图2所示，其中机车长26.200 m，后续车辆长24.175 m；机车与车辆高3.890 m，宽3.260 m。车体之间的车钩及缓冲装置通过非线性弹簧模拟，其力学参数取值依据中国常用车钩及缓冲装置力学性能参数，刚度为2 000 kN·m-1，阻尼系数为40 kN·m-1。

图2 列车有限元模型

构建列车模型时，主要采用4 节点缩减积分壳单元（S4R），车头流线型区域则采用3 节点缩减积分壳单元（S3R），列车单元总数为22 342，网格模型如图3所示。车体材料为铝合金。考虑到车载设备和车辆定额人员也是车辆荷载的组成部分之一，通过在列车模型局部区域嵌入玻璃钢和泡沫材料等实现列车刚度和质量分布的近似等效［18］。列车采用等向强化弹塑性模型，考虑材料的应变率效应，力学参数见表2。

图3 列车网格模型

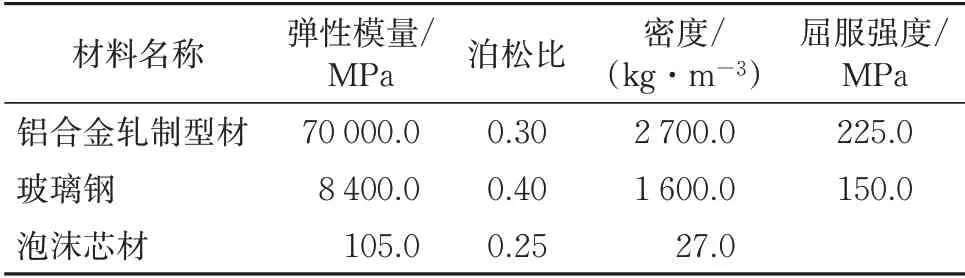
表2 列车材料参数

1.3 脱轨撞击假设条件

营运列车由于车辆和轨道结构破坏、车辆系统蛇形失稳、轨道结构动力失稳以及地震、空气动力等原因可能发生脱轨事故［5］。Grob［19］通过大量调查发现，列车初始脱轨姿态主要包括以下3种：①列车机车（车头位置）脱轨；②列车尾部脱轨；③列车中间段任意相邻两节车脱离轨道。由于列车实际脱轨情况十分复杂，列车脱轨机理也非本文研究重点，因此本文假定列车按照Grob 提出的第1 种方式发生脱轨（机车首先脱轨），脱轨撞击角度为12.5°，列车与衬砌、衬砌与围岩以及衬砌管片间设置面面接触。此时，法向接触行为设置为“硬”接触，可以传递各种接触压力；切向接触行为设置为库伦摩擦接触［20］；接触算法采用罚函数方法，列车的动能通过接触面施加到管片衬砌内表面。根据模型尺寸及脱轨撞击角度，设置列车与隧道衬砌内侧的初始接触位置如图4所示。撞击过程中，列车与隧道衬砌之间的动态接触区域，根据接触算法由有限元程序自动计算识别，相应列车—衬砌—围岩动力分析模型如图5所示。

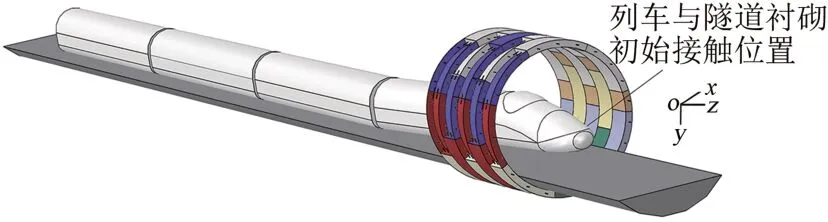
图4 列车与隧道衬砌初始接触

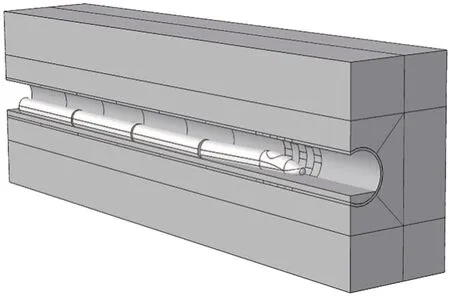
图5 列车—衬砌—围岩动力分析模型

为准确分析不同脱轨速度列车撞击作用下盾构隧道的动力损伤特性，选取列车脱轨速度作为唯一控制变量，并结合我国旅客列车的实际运营速度，按高速（300 km·h-1）、中速（200 km·h-1）、低速（120 km·h-1）3种速度分别进行分析。根据文献［12-13］，列车与隧道剧烈撞击作用主要发生在撞击时刻50 ms 时间范围内。为提高计算效率，按此数值设置计算时长。

2 模型计算结果

基于上述模型，对列车撞击盾构隧道的动态过程进行仿真模拟，提取列车撞击荷载及拉压损伤，分析如下。

2.1 列车撞击荷载

2.1.1 撞击荷载变化规律

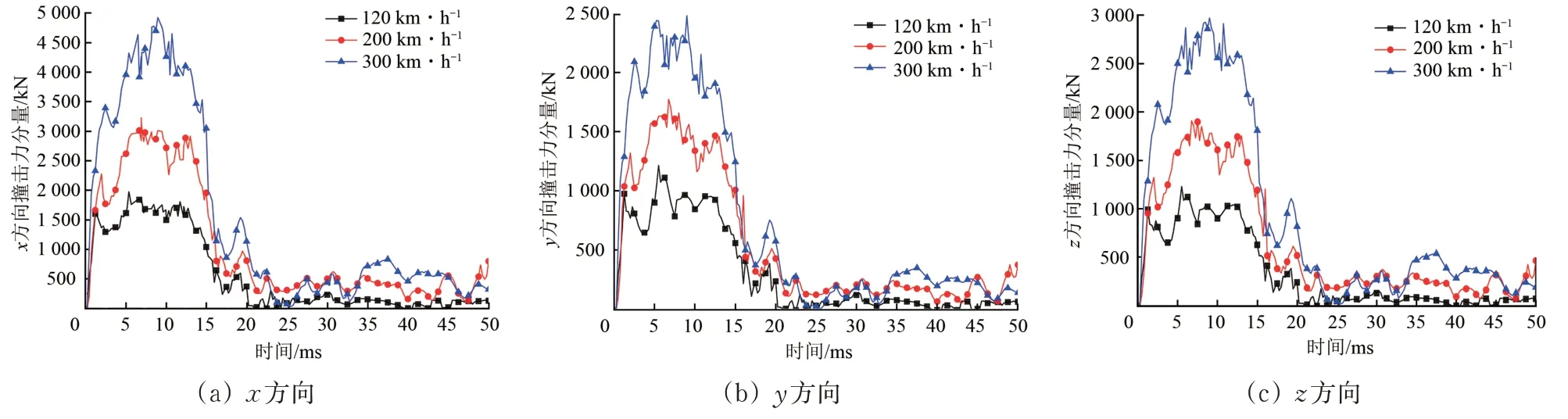
图6 撞击力分量时程曲线

3 种脱轨速度下，列车撞击盾构隧道的撞击力分量时程曲线如图6所示，设x方向为水平面内垂直隧道轴线方向，y方向为竖直方向，z方向为沿隧道轴线方向。由图可知，3 种脱轨速度下，各方向撞击力分量的变化规律基本一致：从列车与隧道衬砌发生碰撞接触开始各方向撞击力迅速增大，在短时间内即达到峰值，之后撞击力震荡减小，在大约25 ms 以后撞击力保持稳定波动。这说明列车与隧道衬砌结构剧烈的撞击作用主要发生在撞击前期，即25 ms 之前；之后撞击作用主要表现为列车与盾构隧道内壁的刮擦接触。由此，根据撞击荷载的变化规律，可将列车与盾构隧道的撞击过程分为初始撞击、碰撞耗能以及稳定撞击3个阶段。

（1）初始撞击阶段，自列车开始与管片衬砌接触，至撞击力达到峰值。此阶段中，列车机车前部与盾构隧道发生接触碰撞，而后续车辆由于惯性的影响仍然以较高的速度运行。由于后续车辆的持续冲击，机车与管片衬砌之间的碰撞力不断增加，并达到峰值。

（2）碰撞耗能阶段，自撞击荷载达到峰值，至撞击后大约25 ms。此阶段中，机车与相接触的管片衬砌均产生较大的变形，列车动能大部分转化为机车以及衬砌管片的塑性耗散能和内能，撞击荷载持续减小。

（3）稳定撞击阶段，自撞击后大约25 ms，至撞击分析结束时间。此阶段中，列车与管片衬砌间剧烈的撞击过程基本结束，列车与衬砌管片主要发生刮擦接触。由于此时列车仍有较高的运行速度，总撞击力保持在一定范围内波动。

2.1.2 撞击荷载峰值对比

整理3 种脱轨速度下，各撞击力分量的峰值以及达到峰值的时刻见表3。可以看出，随列车脱轨速度的增加，各撞击力分量的峰值也在增大，并且撞击力分量峰值发生的时刻也有所延后。

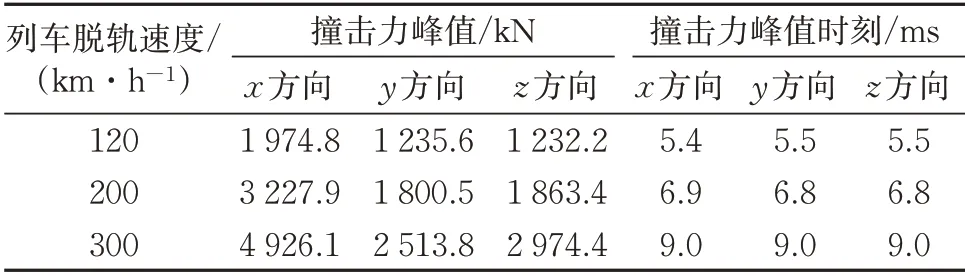
表3 撞击力分量峰值及发生时刻

以x方向撞击力分量为例进行两两比较。当列车脱轨速度为120 km·h-1时，x方向撞击力分量峰值为1 974.8 kN，发生时刻为5.4 ms；当列车脱轨速度增至200 km·h-1时，撞击力峰值为3 227.9 kN，大约是120 km·h-1速度下x方向撞击力分量峰值的1.6倍，发生时刻则延缓1.5 ms。当列车脱轨速度为300 km·h-1时，x方向撞击力分量增至4 926.1 kN，大约是120 km·h-1速度下的2.5 倍，发生时刻则延缓3.6 ms。这说明，撞击分量峰值随列车脱轨速度的增加呈非线性增大趋势。

就3 个方向的撞击力分量做进一步分析可知，x方向撞击力分量的峰值最大，y方向和z方向撞击力分量的峰值相差不多，并且3个方向撞击力分量峰值几乎是在同一时刻达到最大值。

当列车脱轨速度为120 km·h-1时，x方向撞击力分量峰值大约是其他方向撞击力峰值的1.6倍。当列车脱轨速度为200 km·h-1时，x方向撞击力分量峰值与其他2个方向撞击力分量峰值的比值大约为1.7～1.8。当列车脱轨速度增至300 km·h-1时，x方向撞击力分量峰值与其他2 个方向撞击力分量峰值的比值约为1.7～2.0。

将模拟结果与国际铁路联盟2002年发布的UIC777第2 版规范［21］进行对比，当列车脱轨速度为120 和200 km·h-1时，横向撞击力分量峰值分别为1 974.8 和3 227.9 kN，低于规范规定的最大横向撞击荷载3 500 kN。当列车脱轨速度增至300 km·h-1时，横向撞击力峰值则增至4 926.1 kN，超过规范规定值的41%。这意味着，随着我国高铁运营速度的不断提高，在参照国际铁路联盟规范进行结构设计时，需结合实际对规范进行适当修正。

2.2 衬砌管片损伤

为便于分析衬砌管片损伤发展情况，将列车撞击点周围的5 环拼装式衬砌依次编号为：R1，R2，R3，R4，R5。单环管片从封顶块开始沿顺时针方向依次编号为：F1，L1，B1，B2，B3，B4，B5，L2。如图7（a）和图7（b）所示。

模拟可知，列车与盾构隧道的撞击接触主要发生在R1～R3 衬砌环，为此，在列车初始撞击点所在的L1-3管片及其纵向相连的2块管片上（B1-2，L1-1）沿列车行进方向设置15 个观测点，各观测点间距0.5 m，列车初始撞击点为3 号观测点，如图7（c）所示。

数值计算结果显示，3 种脱轨速度撞击下，衬砌管片的损伤演化规律基本一致，但限于篇幅，本文仅以200 km·h-1撞击速度下的盾构隧道为例，研究衬砌管片的拉压损伤发展情况，分析列车撞击对盾构隧道损伤演化的影响。

2.2.1 压缩损伤发展趋势

1）压缩损伤发展及分布

特定时刻下，盾构隧道衬砌管片内、外表面压缩损伤发展情况如图8所示。由图可知，在列车剧烈的撞击作用下，衬砌管片内、外表面均会出现较大程度的压缩损伤。

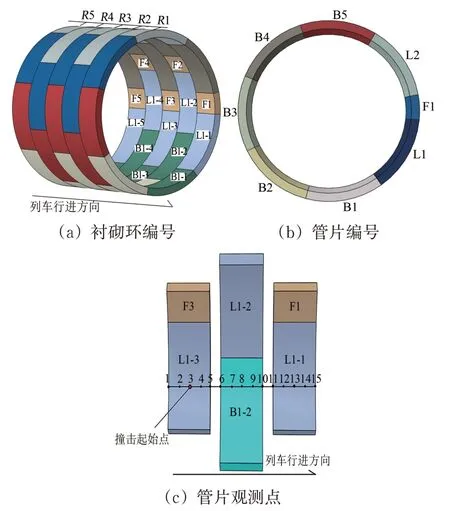
图7 衬砌管片编号及数值观测点

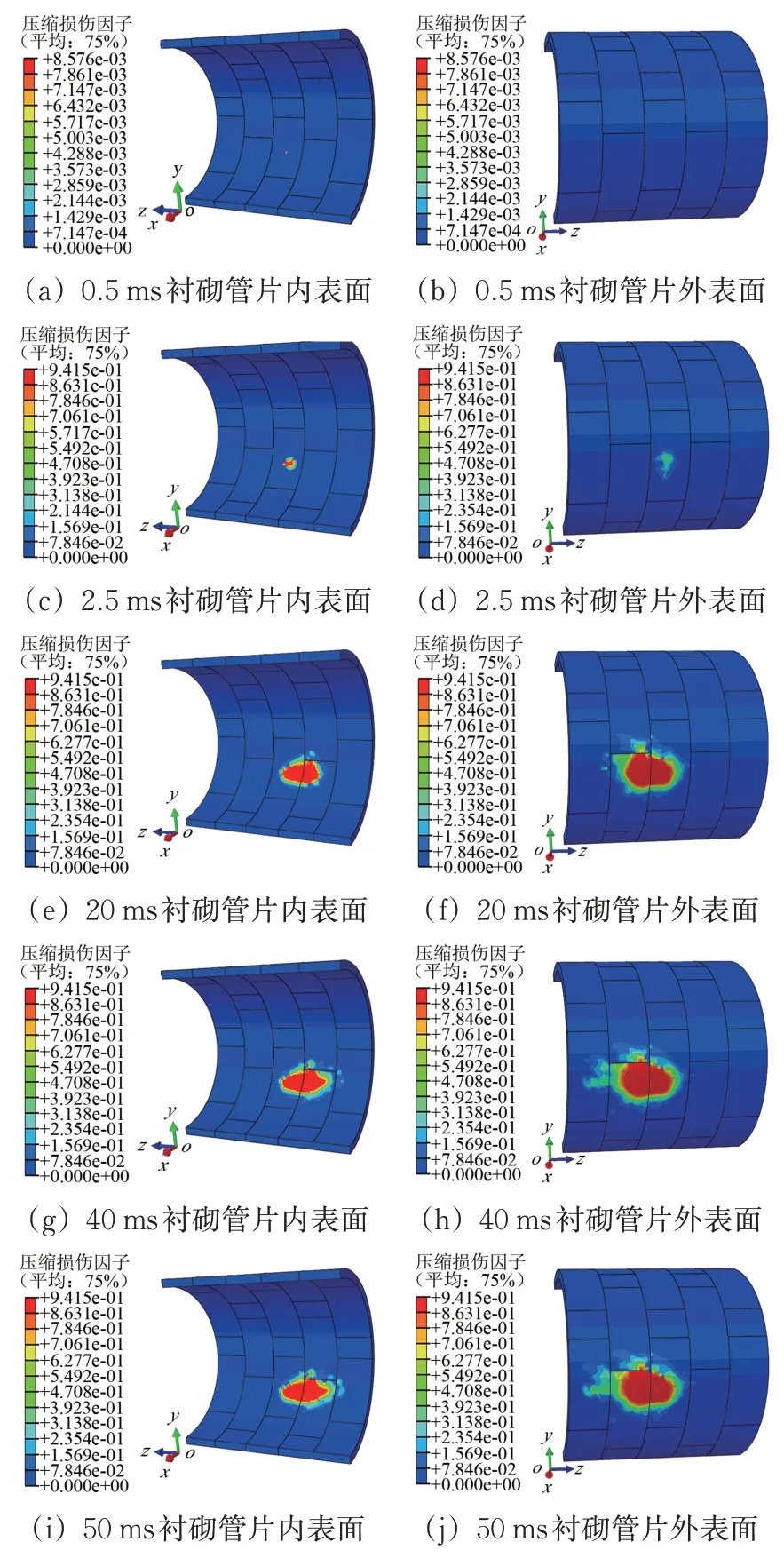
图8 衬砌管片内、外表面压缩损伤演化

从时间的变化来看，0.5 ms 时，在衬砌管片内表面列车初始撞击点附近开始出现压缩损伤，此时管片外表面尚未出现压缩损伤；随着时间的推移，衬砌管片内表面压缩损伤值迅速发展；至2.5 ms 时，衬砌管片内表面压缩损伤最大值已达0.941 5（超过0.9，即表明衬砌结构刚度极大弱化，可能导致隧道出现贯穿性裂缝或局部失稳），此时管片外表面也出现了一定程度的压缩损伤，最大压缩损伤值达0.418；20 ms 时，内、外表面压缩损伤已经从初始撞击管片发展到相邻的管片上，并且外表面的压缩损伤最大值也达0.941 5；20 ms之后压缩损伤的范围逐渐扩大，压缩损伤峰值并无明显增大。

从损伤的分布来看，压缩损伤主要分布在R1、R2 和R3 环的L1-1、L1-2、B1-2、L1-3 这4 块管片上，其中压缩损伤值较大（大于0.9）的区域主要集中在B1-2、L1-3 这2 块管片。在撞击分析结束时刻，压缩损伤分布范围呈现出沿隧道轴向大于环向的“梭形”形态。

总体来看，衬砌管片内表面压缩损伤的发展更为迅速。在撞击分析结束时刻，衬砌管片外表面压缩损伤的分布范围更为广泛。压缩损伤值的发展主要是在撞击初始阶段，之后压缩损伤的演化主要体现为压缩损伤分布范围的扩大。

2）压缩损伤值

撞击结束时，提取各观测点的压缩损伤值如图9所示。由图可知，在列车剧烈的撞击作用下，管片内、外表面各观测点位置都出现了不同程度的压缩损伤，其中压缩损伤较大值（大于0.9）主要出现在观测点3～8。内、外表面压缩损伤最大值均达到0.941 5，此时盾构隧道衬砌管片已发生了较为严重的破坏。

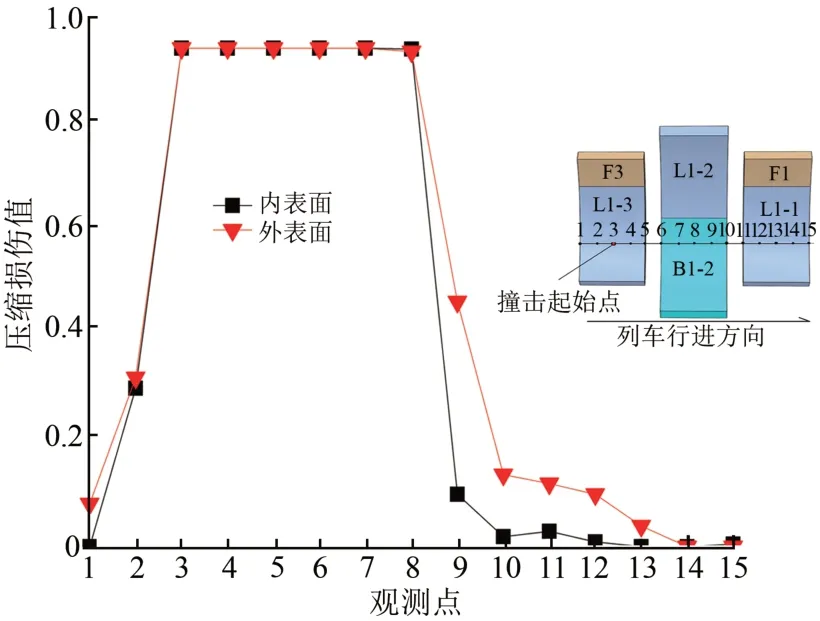
图9 各观测点压缩损伤值

沿列车行进方向，在初始撞击点前边观测点（观测点1 和观测点2）的压缩损伤值处于较低水平。在初始撞击点一定范围内衬砌管片压缩损伤值达到0.9 以上，其后观测点的压缩损伤值迅速降低。在撞击分析时间内，压缩损伤较大值仅分布在初始撞击点所在管片及其邻近管片上。

2.2.2 拉伸损伤发展趋势

1）拉伸损伤发展及分布

具体时刻下，衬砌管片内、外表面拉伸损伤的发展情况如图10所示，与压缩损伤的发展情况基本类似。

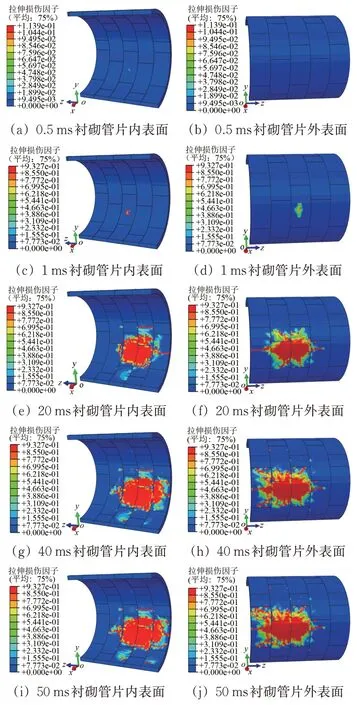
图10 衬砌管片内、外表面拉伸损伤演化

从时间的变化来看，在0.5 ms 时刻，衬砌管片内表面开始出现拉伸损伤，此时管片外表面尚未出现拉伸损伤。在1 ms 时刻，内、外表面拉伸损伤已达到峰值，之后拉伸损伤的发展主要表现为损伤面积的不断扩大。

从损伤的分布来看，与压缩损伤相比，拉伸损伤的分布范围更加广泛，不仅在出现在L1-1、L1-2、B1-2、L1-3 这4 块管片上，在距离初始撞击点一定距离的B1-3，L1-3，L1-4 等管片上也有出现，这与管片混凝土材料较弱的抗拉性能有关。

2）拉伸损伤值

提取撞击分析结束时刻，衬砌管片各观测点位置处的拉伸损伤值如图11所示。由图可知，观测点3～13 位置处内、外表面的拉伸损伤值均达到0.932 7。此时，出现拉伸损伤较大值（大于0.9）的观测点个数是出现压缩损伤较大值个数的1.7倍，说明拉伸损伤更容易导致管片衬砌的大面积破坏。其余各观测点的拉伸损伤值也均表现出外表面大于内表面的特征。

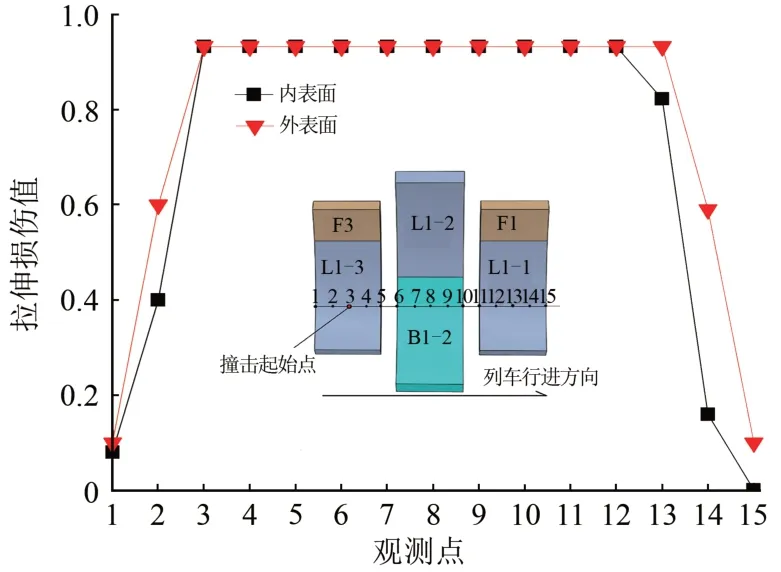
图11 各观测点拉伸损伤值

2.2.3 不同列车脱轨速度撞击下的拉压损伤对比

以3 种列车脱轨速度撞击下，衬砌管片内表面的损伤情况为分析对象，针对撞击分析结束时刻（50 ms），分别构建衬砌管片内表面压缩损伤和拉伸损伤云图如图12-13 所示。可以看出，随着列车脱轨速度的提高，压缩损伤和拉伸损伤的分布范围均显著增大，其中各列车脱轨速度撞击下的拉伸损伤分布范围均相对更为广泛。

1）损伤峰值及损伤面积

进一步分析3 种列车脱轨速度撞击下，衬砌管片内表面压缩损伤和拉伸损伤的峰值以及损伤面积，见表4。可以看出，列车的脱轨速度并不会对压缩损伤和拉伸损伤峰值产生较大的影响，在较小脱轨速度列车的撞击下，衬砌管片内表面仍会产生较为严重的损伤。而列车脱轨速度对损伤面积的影响则十分显著。

以衬砌管片内表面拉伸损伤面积为例。当列车脱轨速度为120 km·h-1时，管片内表面拉伸损伤面积约为16.76 m2；当脱轨速度提高到200 km·h-1时，管片内表面拉伸损伤面积则增至24.04 m2，约是120 km·h-1脱轨速度撞击下拉伸损伤面积的1.4 倍；当脱轨速度进一步提高到300 km·h-1时，管片内表面拉伸损伤面积达到30.51 m2，约是120 km·h-1撞击速度下拉伸损伤面积的1.8倍。

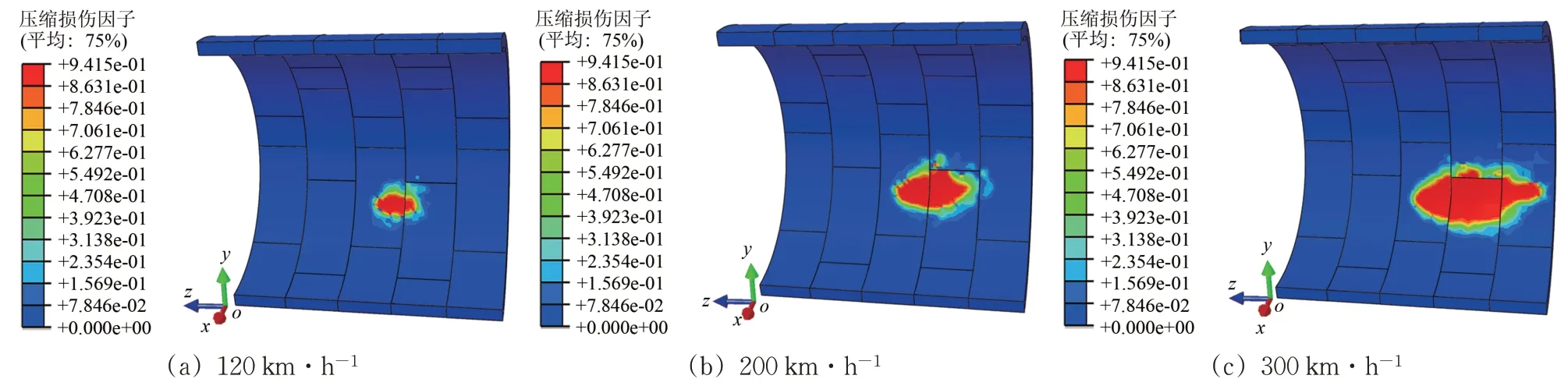
图12 衬砌管片内表面压缩损伤（50 ms）

图13 衬砌管片内表面拉伸损伤（50 ms）

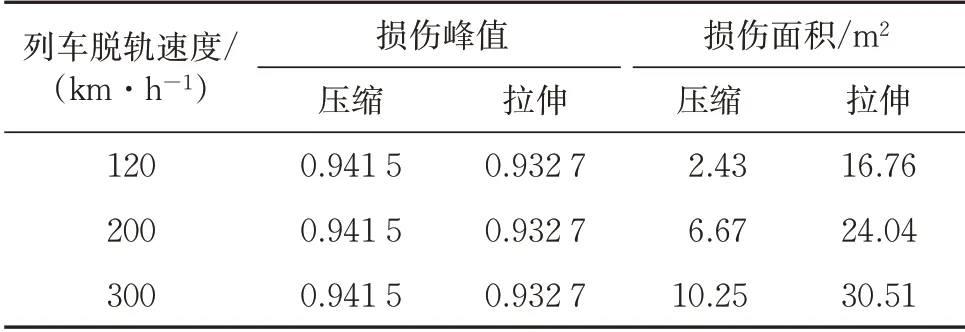
表4 3种列车脱轨速度撞击下衬砌管片内表面压缩损伤、拉伸损伤的峰值及面积

2）损伤分布

就管片内表面的损伤分布范围而言，同一脱轨速度列车撞击下，拉伸损伤的面积始终大于压缩损伤的面积。在撞击分析结束时刻（50 ms），120 km·h-1脱轨速度撞击下拉伸损伤面积大约为压缩损伤面积的6.9 倍，200 km·h-1脱轨速度撞击下拉伸损伤面积与压缩损伤面积的比值为3.6；当脱轨速度提高到300 km·h-1时，管片内表面拉伸损伤面积增至30.51 m2，此时压缩损伤面积为10.25 m2，两者的比值大约为3.0。进一步印证了：与压缩损伤相比，拉伸损伤可能导致衬砌更大范围内的破坏。