残差在线性回归分析中的作用研究

崔俊富 陈金伟 崔 伟

（1.南京航空航天大学经济与管理学院，江苏 南京 211106；2.山东女子学院经济学院，山东 济南 250300；3.南京审计大学经济学院，江苏 南京 211815；4.深圳国育未来教育科学研究院，北京 100875）

一、引言

发现经济变量之间的关系是经济学研究的重要内容，回归分析是比较常用的方法。回归分析将变量分为响应变量和自变量，通过自变量的已知或设定值去预测响应变量的均值。回归分析又可以分为线性回归分析和非线性回归分析，因为优良的性质，线性回归分析的应用性远远超过非线性回归分析。线性回归分析关键是寻找总体回归线使得响应变量的条件均值恰好落在这条线上，即：[1]

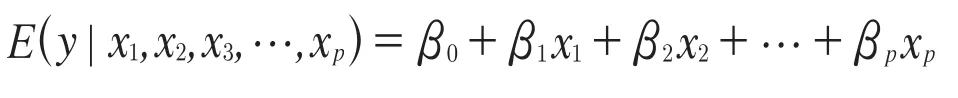
了解总体信息需要耗费巨大的人力物力财力，因此在经济运行分析中总体信息往往是很难获得的。于是统计学相继发展了统计调查和统计推断等领域，其中，统计推断指的是通过样本的信息来推测总体的信息。线性回归分析同样面临总体信息不易获得，而使用样本信息对总体情况进行推断的情况，也就是找到样本回归曲线来推断总体回归曲线，样本回归曲线的函数形式为

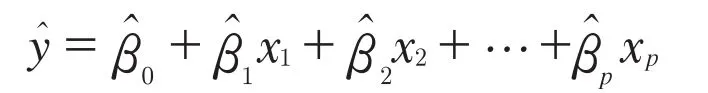
但是，线性方程组可能是相容的，也可能是不相容的。这时形成的线性方程组就是不相容的，无法求解系数。后来数理统计学家指出，统计推断不需要求出能通过所有样本点的回归线，只需要求出距离样本点最近的回归线即可。[2]因为

这个方程组是相容的，可得

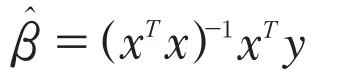
这种求解方式是对样本点的一种“近似”，不能完全反应样本点的信息，也就是说存在一定的误差，真实的样本回归线形式应该是

其中，e为残差项（Residual），反映随机干扰对样本回归的影响，可以认为是随机误差项ε的实现值。经典线性回归模型需要特定的假设，只有当这些假设符合时，才能确保回归模型的准确性，其中最重要的是关于随机误差（残差）的假定，即期望为0；方差为常数；相互独立；自变量与误差项不相关；符合正态分布

二、变量的分布

变量分布是统计研究的重要依据，因为分布决定了变量的性质。了解了参数和响应变量的分布情况，就可以对参数和响应变量的性质进行相应的讨论，例如假设检验、预测分析等等。由于自变量是确定的，参数、响应变量的分布与随机误差（残差）的分布是一致的。随机误差符合均值为0，方差为的正态分布，因此参数和响应变量的分布也符合正态分布。[4]

（一）响应变量的分布

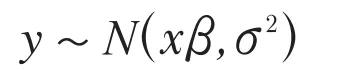
三、回归模型的拟合评价

模型建立仅是拟合数据的第一步，还必须对模型的数据拟合效果进行评价。如果拟合效果不良，说明建立的模型需要进行优化。残差项含有响应变量的部分信息，因此残差就成为判断回归模型拟合效果的重要依据，主要应用于线性检验、模型设定、信息准则等领域。[5]

（一）线性检验

参数的显著性检验反映了自变量对于响应变量模拟是否有贡献，通过了显著性检验可以确定该参数对应的自变量对于响应变量模拟有贡献，未通过显著性检验可以确定该参数对应的自变量对于响应变量模拟没有贡献。

（1）分参数检验

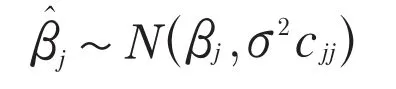
其中，cjj为矩阵

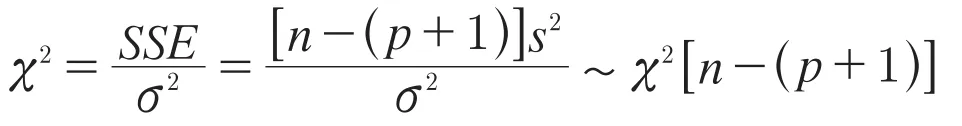
如果上述t统计量超过了显著性水平确定的临界值或者由该t统计量计算的P值过小，那么可以拒绝零假设，也就是分参数不为0。[3]

（2）总体线性检验

分参数t检验可以了解每一个参数的情况，但是参数较多的时候单独进行检验效率不高，而且t检验的次数过多会使得犯错误的概率加大，或者不需要知晓每一个参数的具体情况只需要了解总体线性情况，这时可以选择总体线性检验。[6]在原假设β1=β2=…=βp=0的情况下，构造统计量

F统计量和决定系数R2的构造都用到了SST=SSR+SSE，可以确定二者之间存在联系，通过变换，二者可以相互导出。相对而言，决定系数R2比较粗糙，F统计量比决定系数R2具有更严格的统计理论支撑，更加准确。

（二）模型设定

自变量选择是多元线性回归模型构建的关键内容，是选择线性的模型还是非线性的模型，是选择少变量形式还是多变量形式都需要讨论。

（1）失拟检验

失拟指的是所选择的模型可能是错误的，不能拟合现有的数据，也就无法得出有意义的结论。最初的失拟检验需要对不同的自变量的值进行重复观测，假定响应变量在xi水平上有ni个值，yij表示第j个观测值，则残差平方和可以表示为

如果上述F统计量超过了显著性水平确定的临界值或者由该F统计量计算的P值过小，那么可以拒绝零假设，也就是存在失拟，模型需要重新设定。上述检验要求获得在xi水平上的重复观测值，实际情况当中，特别是多元线性回归中很难获得重复观测值。Daniel和Wood（1980），Joglekar，Schuenemeyer和 LaRiccia(1989)利用最近邻的思想来近似作为重复观测值，进而进行失拟检验，得出了一些有益结论。[7-8]

（2）比较嵌套检验

嵌套模型也经常用于自变量选择问题，所谓嵌套模型指的是构建两个以上的模型，其中一个模型包含另一个模型的所有变量，并且至少包含一个以上的其他变量，使用嵌套模型可以非常有效地比较自变量是否对解释响应变量有贡献，而且可以一次检验许多自变量。可以构建[9]

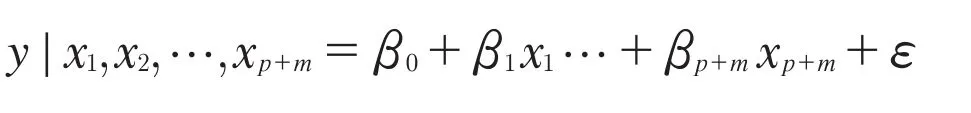
对于自变量xp+1，…，xp+m是否贡献了有价值的信息，在原假设βp+1=…=βp+m=0的情况下，可以构造统计量

其中，SSER为简化模型残差平方和，SSEC为完全模型残差平方和。如果上述F统计量超过了显著性水平确定的临界值或者由该F统计量计算的P值过小，那么可以拒绝零假设，也就是完全模型比简化模型可以对响应变量提供更强的解释力。

（三）信息准则

除了失拟检验和比较嵌套检验外，自变量的选择还可以最小化赤池信息准则（AIC）、施瓦茨信息准则（SBIC）和汉南—奎因信息准则（HQIC）[5]

其中，L为似然函数

上述准则的基本思想都是对所添加的回归变量施加惩罚，当所增加的回归变量减少AIC、SBIC和HQIC时，才增加该回归变量，否则就不能增加。因为信息准则需要S2来导出，因此该方法实际上也是考察残差信息的变化。[10-12]

四、回归模型的预测

除了对现有的数据进行描述，回归模型最重要的应用是进行预测。已经知道，利用现有的数据建立的回归模型存在随机误差，那么回归模型预测的数据也必然存在误差，而且预测数据的误差与现有数据描述的残差存在联系，这种联系通过影响预测数据的分布得以体现。[13]

（一）响应变量均值的预测

可知，E(y)在置信水平100×(1-α)%的置信区间为

（二）响应变量个别值预测

响应变量预测的随机误差为[1]

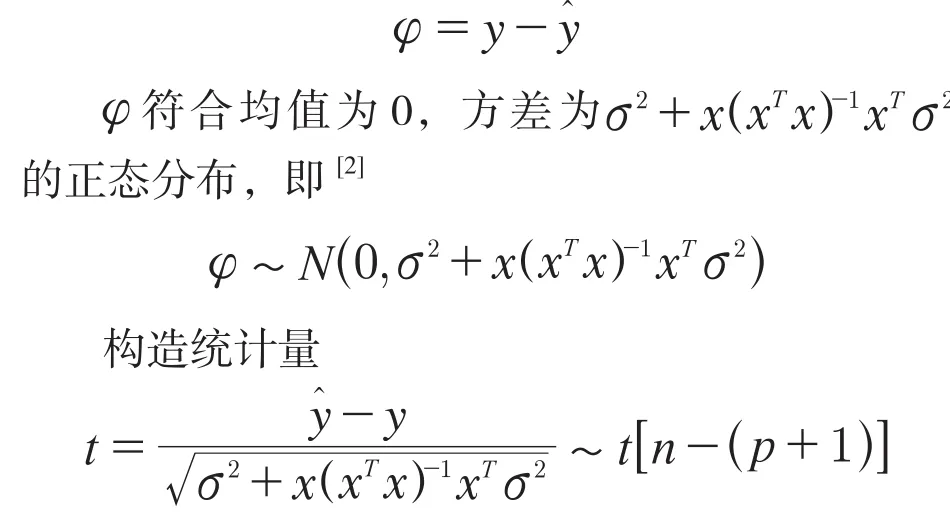
可知，y在置信水平100×(1-α)%的置信区间为

五、假定与异常值诊断

线性回归模型的有效性需要残差符合若干假定，只有符合这些假定才能导出参数、响应变量的分布，进行假设检验，预测响应变量。一旦假定不符合，线性回归模型的有效性就受到很大影响。如果零均值假定不符合，那么上述对于参数、响应变量、响应变量预测值的期望的讨论将不再有效，难以知晓这些变量的均值情况。如果常数方差假定不符合，那么参数、响应变量、响应变量预测值的方差将不可获知。如果正态分布假定不符合，意味着参数、响应变量、响应变量预测值也不能用正态分布进行描述。对于这些假定不相符可以使用一些方法加以克服，例如对数变换、广义最小二乘法等等。残差不符合假定一种常见原因是有异常值，某几个异常值就可能导致残差出现较大波动。通过观察残差可以帮助确定异常值，主要有4种方法，分别是标准化残差、学生化残差、PRESS残差和R-学生化残差。[14]标准化残差相对简单直观

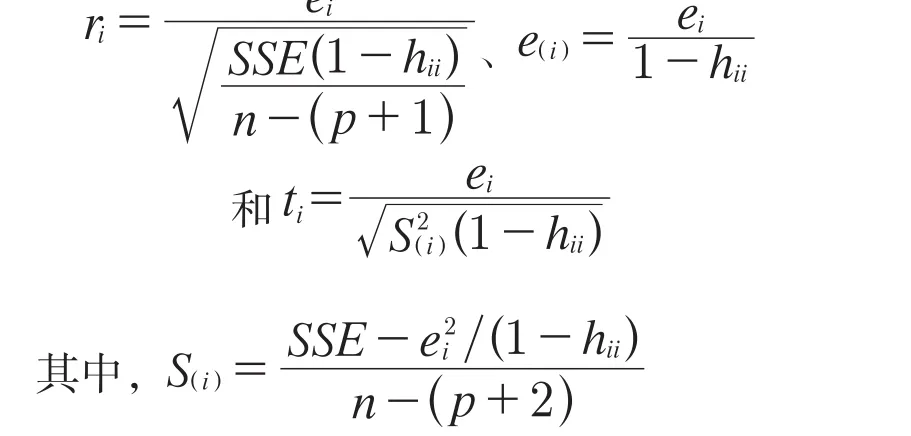
如果某一个数据点的标准化残差、学生化残差、PRESS残差和R-学生化残差远远大于其他数据点，那么基本可以判断该点为异常值点。异常值的出现可能出现两种结果，一种是杠杆点，不影响模型拟合，另一种是强影响点，对模型的拟合有较大影响。前者可以通过矩阵h对角线元素的值来进行判断，后者可以参考库克距离。[15-16]

库克距离较大的点对参数的估计有较大的影响，如果剔除第i个点估计的参数出现了较大的移动，例如达到了库克距离确定的置信域边界，那么该点为强影响点。异常值的出现通常意味着比较艰难的选择，异常值含有部分信息，有可能这些信息是模拟需要的关键信息，删除异常值可能使模型拟合的更好，但是可能丢失了关键信息，而不处理异常值又影响了模型拟合，所以对于异常值的处理要非常的谨慎，最好的方式是收集更多的数据帮助进行更准确的判断。

六、结语

发现经济变量之间的关系是经济学研究的重要内容，回归分析是比较常用的方法。数据的随机性导致线性回归模型分成回归项和残差项两个组成部分，回归项解释的响应变量信息越多，说明回归模型性质越优良，反之，残差项解释的响应变量信息越多，说明回归模型性质越差。本文对残差在回归分析中的作用进行了总结讨论，发现残差的信息可以帮助确定数据分布、进行拟合评价、预测响应变量、判断异常值等。因此，对残差进行分析不仅可以确定线性回归模型的拟合情况，还可以帮助模型的优化调整。线性回归模型建立并模拟数据集之后，一定要通过观察残差分布图，进行正态分布检验等形式对残差进行分析讨论，挖掘残差当中有价值的信息，从而准确判断现有模型的价值并加以优化。