少数决:更安全的分布式一致性算法选举机制*
2020-10-15姜建国
李 彬,姜建国
1.北京交通大学计算机与信息技术学院,北京 100044
2.国家保密科技测评中心,北京 100044
3.中国科学院信息工程研究所,北京 100093
1 引言
现实生活中,选举就是让符合多数人想法或利益的人获得领导权,被选举者需要大多数人或大多数有投票权人的赞同,即多数者决策。这个在人类社会中的民主模式启发并影响了分布式系统一致性算法研究者们,经典的一致性算法Paxos的选举机制就是如此。它的Leader选举分为两个阶段[1],且两个阶段无法分割、相互关联共同保障了数据的一致性。第一阶段:准备阶段,提案者(proposer)选择一个提案号,并发送提案给投票者(acceptor),试探能否得到多数派投票者的响应。第二阶段:如果某个提案者在第一阶段收到多数派投票者的响应,则提交提案,如果能够再次得到多数派acceptor的同意,则这个提案者被选为Leader。显然,这两个阶段都是采用多数决的方式。其实,分布式系统中各个服务器并不在乎Leader是谁,Leader是否意识形态与自己一致,是否为民主选举,他们需要的只是能非固定地选出一个服务器,它能按照协议履行相关职能,让系统保持数据更新一致。本文将提出“少数决”这一新的选举机制,通过研究分析此种选举不仅是简单的逆向思维,还在保护去中心化,提高一致性算法安全性上有更好的表现。
2 基于选举的一致性算法面临的风险
首先,Multi-Paxos[2]、Raft[3]、ZAB[4]、VR(viewstamped replication)[5]这些已实际应用的一致性算法其实都是基于选举的一致性算法。Multi-Paxos中的Leader是作为对经典Paxos的优化而提出,通过选择一个proposer作为Leader降低多个提案者引起冲突的概率,提升性能将一次决议的平均消息代价缩小到最优的两次,而且当有多个Leader存在时算法也仍是安全的,只是退回为经典Paxos选举。而Raft、ZAB、VR这些强调唯一Leader的协议,它们直接从Leader的角度描述协议的流程,但是实际上它们使用了和Paxos完全一样的原理来保证协议的安全性,当同时存在多个节点同时尝试成为Leader或者多个节点都认为自己是Leader时,它们也将退回至经典Paxos选举[6]。
在基于选举的分布式系统中可能存在这么一种问题节点:它们不同于传统的拜占庭将军问题[7](Byzantine failures)节点,不会故意发出错误的更新去破坏系统数据的一致性,但是它们会在选举谁作为Leader时操作选票,目的是让指定的节点获得Leader特权,从而垄断客户业务。这种自私行为本身违背了去中心的原则,一旦这个被指定的节点遭受攻击或故障,将是灾难性的系统崩溃。因此,需要选择更安全的一致性算法选举机制来提升整个分布式系统的安全性。
3 现实中的少数决选举
现实中少数决选举来源于Liar Game中的Minority Decision[8],它并不牵扯少数者博弈[9]问题,本是一个纯粹基于随机目的选择“幸运儿”游戏,具体规则如下:
首先,组织者随机选择一名参与者出一道二选一的题目,如“你是否喜欢红色?”。为充分保证公平性,一般是一人出一题后就换下一个人出题,出题顺序无特殊要求,总之大家都有公平的机率出题即可。
接着,大家根据题目和自己想法做出“是”或“否”的选择。这里需要说明的是大家的选择并不一定是自己真实的想法,需要思考是:怎么让自己的选择不是大多数人的选择?但可以肯定的是绝不能让别人知道你的选择,因为如果有人知道足够多人的选择后,他就能做出少数选择。因此,现实中最简单的方法就是将选择写在纸上后折叠,再投入一个不透明的箱子中。
一次选举包含多轮答题,每轮答题结束后,由组织者唱票。选择为少数派的那一方获胜,进入下一轮继续进行出题、答题;而选择为多数派一方遭淘汰;如双方人数持平或大家选择都一致,则无淘汰者,并直接进入下一轮。
最后,可能是剩下一个人或是两个人,一个人时直接宣布胜出;两个人时则组织者参与进来以打破两人无法产生少数派的僵局,进行决赛。假设进入决赛的两人为A和B,组织者为Z。如果不是A或B的选择为少数派(即Z胜出),则A、B和Z继续下一轮,直至A或B胜出。
根据上述规则描述,可以归纳此种选举机制的流程如图1所示。

Fig.1 Minority election mechanism process图1 少数决选举机制流程
下面举例进行说明,假设参与者为10人,分别为P1,P2,…,P10,组织者为Z。例1:第一轮P1、P2、P3、P4选择Yes,其余人选择No,则P1、P2、P3、P4进入下一轮;第二轮P1、P2、P3选择Yes,P4选择No,则P4获胜。例2:第一轮P1、P2选择Yes,其余人选择No,则P1、P2进入下一轮(决赛);第二轮P1、P2选择Yes,Z选择No,则无人淘汰进行下一轮;第三轮P1和Z选择Yes,P2选择No,则P2获胜。例3:第一轮P1、P2、P3、P4、P5选择Yes,其余人选择No,平局无人淘汰进行下一轮;第二轮P1选择Yes,其余人选择No,则P1获胜。
4 安全性分析
多数决选举中最常见的一种作弊方式就是控票,控制半数以上有投票权的人的选票,就能保证自己想让谁当选就让谁当选。在经典Paxos中可以更容易些,因为只有acceptor(投票者)能投票,所以只要控制50%以上的acceptor就能随心所欲地指定Leader。而在类Raft这种每个节点都有投票权的系统中实现控票,则需要控制50%以上的节点。本章将分析采用少数决选举机制是否也存在类似的安全性问题。为方便分析,本章假设是由22个参与者组成的少数决选举系统。
4.1 绝对控制攻击
在这22个参与者组成的少数决选举系统中,如果已经控制了其中的12个参与者的选票(超过50%),接下来是否能够完全按照自己的意志选择Leader。假设P1,P2,…,P22为22个参与者,P1,P2,…,P12组成受控团队。假定想指定P1成为Leader,就必须保证P1能100%顺利通过3轮的淘汰,因此团队采取全力保证P1和尽可能多的队友进入下一轮的方式进行投票。第一轮,因为还是不知道团队外这10个参与者的选择,所以要保证P1能进入第二轮,只能让P2,P3,…,P12这11个队友选择Yes,P1选择No,这样才能保证结果最坏是平票(因为有可能团队外的10个参与者也同时选择No),但只要这10个参与者是未经商量随机投票的,总会有一轮它们会选择不同的答案。但是,这样做后第二轮又变成公平的10选1选举了,P1将只有10%的获胜几率。
加大攻击力度,分析在控票率达到81.8%(18/22)的情况下是否可以保证P1获胜。第一轮,因为不知道团队外P19、P20、P21、P22的选择,所以要保证P1能进入下一轮,先能让P1,P2,…,P7这7个队友选择Yes,P8,P9,…,P18这11个队友选择No,这样才能保证结果最坏是平票(P19、P20、P21、P22同时选择Yes),但只要P19、P20、P21、P22是未经商量随机投票的,总会有一轮其中会有参与者因选择No而遭淘汰。假设第一轮P20、P21、P22选择Yes,P19选择No,因此P1,P2,…,P7和P20、P21、P22进入下一轮。第二轮,同理P1、P2这2个队友选择Yes,P3、P4、P5、P6、P7这5个队友选择No,最坏情况,假设第二轮P21、P22选择Yes,P20选择No,因此P1、P2和P21、P22进入下一轮。第三轮,P1、P2无论怎么作弊,都无法保证P1获胜。这表示控制81.8%的选票只能将P1获胜的几率提升至25%,且其他少于18个队友的团队也都无法保证P1的100%获胜。
再次加大攻击力度,分析在控票率达到86.4%(19/22)的情况下是否可以保证P1获胜。第一轮,因为不知道团队外P20、P21、P22的选择,所以要保证P1能进入下一轮,先能让P1,P2,…,P8这8个队友选择Yes,P9,P10,…,P19这11个队友选择No,这样才能保证结果最坏是平票(P20、P21、P22也选择Yes),但只要P20、P21、P22是未经商量随机投票的,总会有一轮其中会有参与者因选择No而遭淘汰。假设第一轮P21和P22选择Yes,P20选择No,因此P1,P2,…,P8和P21、P22进入下一轮。第二轮,同理P1、P2、P3这3个队友选择Yes,P4,P5,…,P8这5个队友选择No,这时最坏情况又是平票,逼P21和P22至少一个淘汰,否则永远平票。假设P22选择Yes,P21选择No,因此P1、P2、P3和P22进入下一轮。第三轮,同理P1选择Yes,P2、P3这2个队友选择No,P22注定被淘汰,而P1通过一系列操作终于获胜了。
根据上面分析可以得出,少数决中绝对控制攻击需要满足一个十分苛刻的条件才能确保攻击成功,表1列出了参与者分别为3至30个时保证绝对控制攻击成功所需要的受控个数,图2展示了对应的所需受控率。

Table 1 Number of controls required for success of absolute control attack with 3 to 30 participants表1 参与者为3至30个时绝对控制攻击成功所需受控数
分析表1和图2,可以看出:
(1)参与者为4个时,控票率达到75%(3/4)时,是少数决遭受绝对控制攻击所需控票率的最低值,即最易受攻击状态;
(2)参与者为10个时,是一个低值(下划线标记的),此时控票率需达到80%(8/10);
(3)参与者为22个时,是另一低值,此时控票率需达到86.4%(19/22);进而推论随着参与者的增加,低值出现的频率将越来越低,且低值也越来越高,即攻击难度越来越大。
4.2 团队攻击
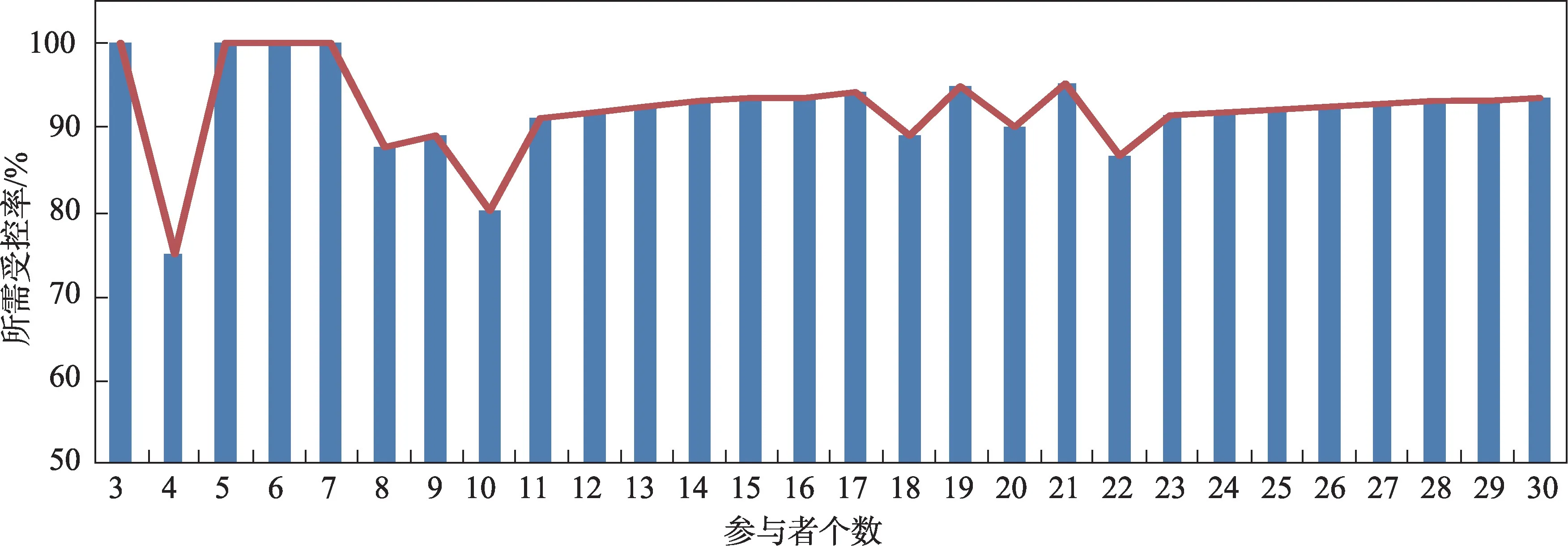
Fig.2 Control rate required for success of absolute control attack with 3 to 30 participants图2 参与者为3至30个时绝对控制攻击成功所需受控率
如果能成功控制一定数量节点的投票,是可以保证这个团队中的一个最终获胜,即团队攻击成功。第一轮中,安排团队中的8个节点中4个节点选Yes,另4个节点选No。因此这一轮后留下来的节点中总有团队中的4个,最坏情况下还有4个团队外的节点。第二轮中,安排团队中的4个队友中2个选Yes,另2个选No。因此这一轮后留下来的节点中总有团队中的2个,最坏情况下还有2个团队外的节点。第三轮中,团队中的2个队友中的1个选Yes,另1个选No,只要另外两节点是未经商量随机投票的,总会有一轮它们选择同样的答案,于是最终成为Leader将是团队中的一员。
要保证在少数决选举团队攻击成功,团队成员的数量Tn要满足一定条件。Tn与可能进行的有效投票轮数r(平局轮不计,r与参与者总数An相关)有关,因此当控制节点数量Tn满足Tn≥2r时可以确保团队攻击成功。
但是,团队攻击只能保证团队中的某一个成员被选为Leader,但仍然无法确定最终获胜的是哪一个,即只是缩小了产生Leader的节点范围,降低了系统去中心化的程度。
4.3 欺诈攻击
首先,假设P1找到P2,P3,…,P8等7个参与者在不为人知的情况下组成一个团队,把保证团队获胜的方法告诉团队成员,并承诺团队获胜后平分作为Leader的权益。然后,P1再找P9,P10,…,P15等7个参与者秘密地组建第二支团队,策略和承诺相同。最后,P1再与剩余的P16,P17,…,P22秘密地组成第三支团队。这里成功地组织了3支“8人”团队,让每个参与者都坚信自己身在一个将要利用必胜法获胜并平分胜利果实的团队里。除了P1,大家都不知道还有其他团队存在。在第一轮游戏中,P1指示每个团队里包括P1自己在内的4个队友投Yes,其余的人都投No。这样下来,投Yes的一共就有10票,No有12票,于是P1和每个团队里除P1之外的另外3个人获胜。下一轮游戏中,P1再指示每个队伍里包括P1在内的2人投Yes,其他人都投No,这样Yes就有4票,No有6票,P1再次胜出。最后,P1自己投Yes,并指示其他人都投No,这就保证了P1可以100%获胜。
这种攻击方式因其在现实中确实存在理论上的可能,但在没有奖励机制、没有智能协商、需要重复多次选举的分布式系统中是不可能实现的,因为把一致性算法当作共识机制的分布式系统,被设定是不存在拜占庭将军问题的。
5 少数决在一致性算法中的实现
本文认为可以利用少数决选举的科学性产生一致性算法中的随机Leader。通常来讲,一个正确的一致性算法需要满足以下3条性质:
安全性:具备安全性的算法保证坏的事情绝对不会发生,例如分布式Leader选举算法,绝对不会出现一个以上进程被选为Leader的情况。
存活性:具备存活性的算法保证好的事情终将发生,即算法在有限的时间内可以结束。
去中心性:在去中心化系统中,任何人都是一个节点,任何人也都可以成为一个中心。任何中心都不是永久的,而是阶段性的,任何中心对节点都不具有强制性[10]。
作为一致性算法中最关键的选举机制设计也应具备上述3个性质,下面将给出少数决选举机制的一个设计方案。
5.1 去中心化
因为分布式系统是去中心化的,所以不能固定设置一个组织者角色。另外,由组织者承担出题者的职能是没有任何问题的,因此组织者可以是由所有节点轮流承担,即每进行一轮就换一个组织者,避免中心化的问题。这种轮换机制,可以是简单地按ID号i从小到大顺序轮转,然后最大号码链接1号的方式,即1 →2 →3 →…→max→1 →2…,也可以采用其他轮换机制。
5.2 统计参与者范围
采取少数决选举分布式系统的每个节点是需要知道整个系统节点个数An,之后增加或减少节点个数时要及时更新An,并且设置初始化判断胜负的关键计数器n=An。
5.3 题目及计票方式
根据第3章描述的少数决选举特点,题目并不要求难度只是需要二选一的题目,这就自然而然让布尔值成为首选。而题目竞猜也可转变为:猜二进制随机数的最后一位、域名服务器ping值的奇偶性等方式。只要是能够产生具有随机性的布尔值,且布尔值出现的概率为50%的方式[11]均可作为少数决的题目。下面将以猜二进制随机数的最后一位为例进行描述。
如由An个节点组成的分布式系统,每个节点产生一个随机数Rn,并将自己ID信息Answ(Rn,i)一同发送给组织者,组织者将使用Lr(i)函数剥离i所对应随机数二进制格式时的最后一位。需按照式(1)计算j,如果j=n/2、j=n或j=0则表示没有淘汰者,每个节点重新产生随机数;j>n/2则Lr(i)=0对应的节点ID号进入下一轮比赛名单,设n=n-j;否则,Lr(i)=1对应的节点ID号进入下一轮比赛名单,设n=j。

5.4 存活性
少数决选举的存活性问题,就是Leader可以在有限的时间内选举出来,进而推论就是二选一答题是否可以在有限次数内结束。显然,少数决选举中的二选一答题问题相当于掷硬币问题。利用高斯分布函数[12]式(2),可得出以下结论:当观测结果的正面向上次数远远大于正面向下次数,也远远大于先验分布[13]的正面向下次数,则判断下次为正面向上的概率无限接近1[14]。
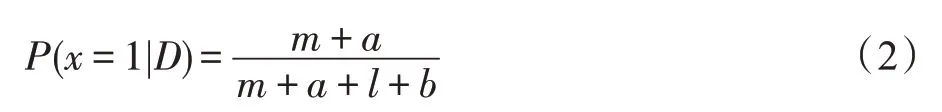
式中,a、b、m、l分别代表先验分布的正面向上次数、反面向上次数、已观测数据的正面向上次数、反面向上次数。
上述结论说明了,随着答题次数的增加,每个答题者的答案会一直变动,极小概率会出现所有人答题结果都一致或结果永远是50%对50%的情况。因为小概率事件可视为不可能事件,所以二选一答题可以在有限次数内结束。
5.5 组织者的期号
为避免由于通信延迟、重发等原因造成一个少数决系统中出现两个或者两个以上的组织者,造成混乱,每个组织者都需要附加一个期号(term)。这里的期号使用可参考Raft算法中的实现方式[3],每次轮换组织者期号就会递增,答题者只跟随期号大的组织者进行持续竞选。
5.6 组织者
组织者只需要接收本轮比赛名单内的答题者的答案,初始名单为所有节点。组织者需要通知大家本轮答题开始,让答题者将随机数Rn发送给自己。这个通知信息包含自己的期号和下一任组织者的ID信息,如M1(term,NextqwID)。
5.7 信息保密性和身份认证
可以通过非对称加密算法[15]保证答题者随机数的保密性和确认答题者、组织者身份。非对称加密算法实现保密信息交换的基本过程是:每个节点生成一对密钥并将公钥公开;当答题者需要向组织者发送信息的时候使用组织者的公钥对随机数信息进行加密后再发送给组织者;组织者再用自己私钥对加密后的信息进行解密。此外,非对称加密算法实现身份认证的基本过程是:答题者可以使用自己的私钥对需要发送的信息进行签名后再发送给组织者;组织者再用答题者的公钥对答题者发送回来的数据进行验签,确认其身份。
反之,组织者给答题者发送信息的加密方式和组织者的身份认证也将采取上述方式,这里不再赘述。
5.8 唱票方式
组织者需要将期号、计票结果、进入下一轮的节点ID号、本轮每个答题者的答案等信息,如M2(term,result,NRA_IDs,Answs(n)) 通过广播方式告知本轮的每个答题者,以示公允。
M2中的信息越详细越能体现公正性,因为每个答题者是可以通过M2发现当前组织者是否有篡改答题结果或计票错误等作恶行为。这里不必采取冷酷策略,即发现某组织者出现一点儿错误就终止其参与资格,因为可能会无法区分主观作恶和客观网络传输错误。可通过EigenTrust[16]、PeerTrust[17]等网络节点信任评价方法,对该恶意节点做出临时屏蔽或永久去除等惩罚措施。
5.9 容错处理
在少数决选举进行的过程中,可能会出现一些故障,如节点宕机或通信受阻的情况,下面描述两种最常见故障的处理方式。
(1)答题者中途宕机。由于答题者可能宕机或通信受阻,在规定时间内收到的答案个数num(Answs)少于2个时,代表整个系统出现严重故障,本次选举终止,按照ID号轮换下一个节点继续出题;如果num(Answs)大于2个但少于预期个数n时,重置n(n=num(Answs));如果计票结果为平票时,本轮无淘汰节点,直接进行下一轮答题;如果计票结果可以分出胜负时,将未收到答案的答题者列为淘汰方,获胜者继续进行下一轮答题。
(2)组织者中途宕机。答题者在发送一个答案给组织者后,一定时间内未收到组织者的计票结果时,首先询问查看组织者状态,如果确认是组织者宕机且下一任组织者不是自己,就等待下一任组织者的广播信息,准备下一次答题;如果自己是下一任组织者,累加期号后广播自己成为组织者的消息,准备出题。
5.10 决赛问题
按照现实中的游戏规则,决赛是需要组织者这个固定角色参与的,但在前面去中心化设计并已去掉了这个固定的角色的情况下,可以通过另一种方法解决此事。首先对比两个节点ID号i1和i2,如果i1>i2,则Mid=i1,Lid=i2;如果i1<i2,则Mid=i2,Lid=i1。再对比两个节点的答案Lr(i1)和Lr(i2),如果决赛两节点的答案是相同的,即“11”或“00”,就判定Lid对应的那个节点当选;如果是不同的,即“01”或“10”,就判定Mid对应的那个节点当选,这样依然能够保证Leader选举的随机性和公正性,形式化后的计算公式如式(3)所示。

5.11 组织者核心算法伪代码


6 实验验证
本实验主要是在单台计算机上,通过多个虚拟终端来仿真多台计算机之间的通信过程,对比多数决和少数决选举机制的选举速度和安全性。采用C语言实现少数决选举;通过修改的开源libPaxos实现多数决选举,并设所有服务器均承担proposer和acceptor两种角色;实验环境为Dell Precision移动工作站,Intel Core i9-8950HK,2.9 GHz,32 GB DDR4内存,操作系统为VMware Workstation虚拟机下的Ubuntu 16.4.04。
6.1 选举成功率
模拟同一网段内的8台集群服务器。通过分别执行1 000次多数决和少数决选举,对比两种选举机制的规定时间内选举成功次数[18]。图3展示了在250 ms、500 ms、1 000 ms内,模拟集群服务器分别运行多数决和少数决选举机制,成功选举出Leader的次数。
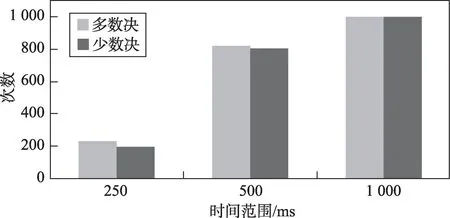
Fig.3 Comparison of the number of successful elections within specified time图3 规定时间内选举成功次数对比
6.2 选举安全性
模拟同一网段内的8台和10台集群服务器两种场景。通过执行多数决和少数决选举,对比两种选举机制的安全性。多数决时采用共同投票给P1的方式进行攻击,少数决时采用本文4.1节描述的:全力保证P1和尽可能多的队友进入下一轮的方式进行攻击。
图4是在受控节点分别为1,2,…,8的情况下,分别采用经典Paxos的多数决选举机制和少数决选举机制各进行20次Leader选举,统计拟定对象P1的获胜次数。图5是在受控节点分别为1,2,…,10的情况下分别采用经典Paxos的多数决选举机制和少数决选举机制各进行20次Leader选举,统计拟定对象P1的获胜次数。
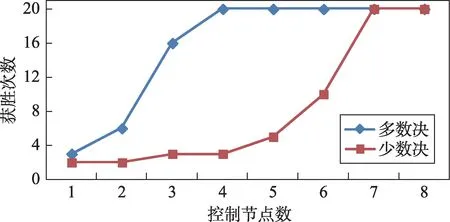
Fig.4 Comparison of election security of 8 cluster servers图4 8台集群服务器选举安全性对比
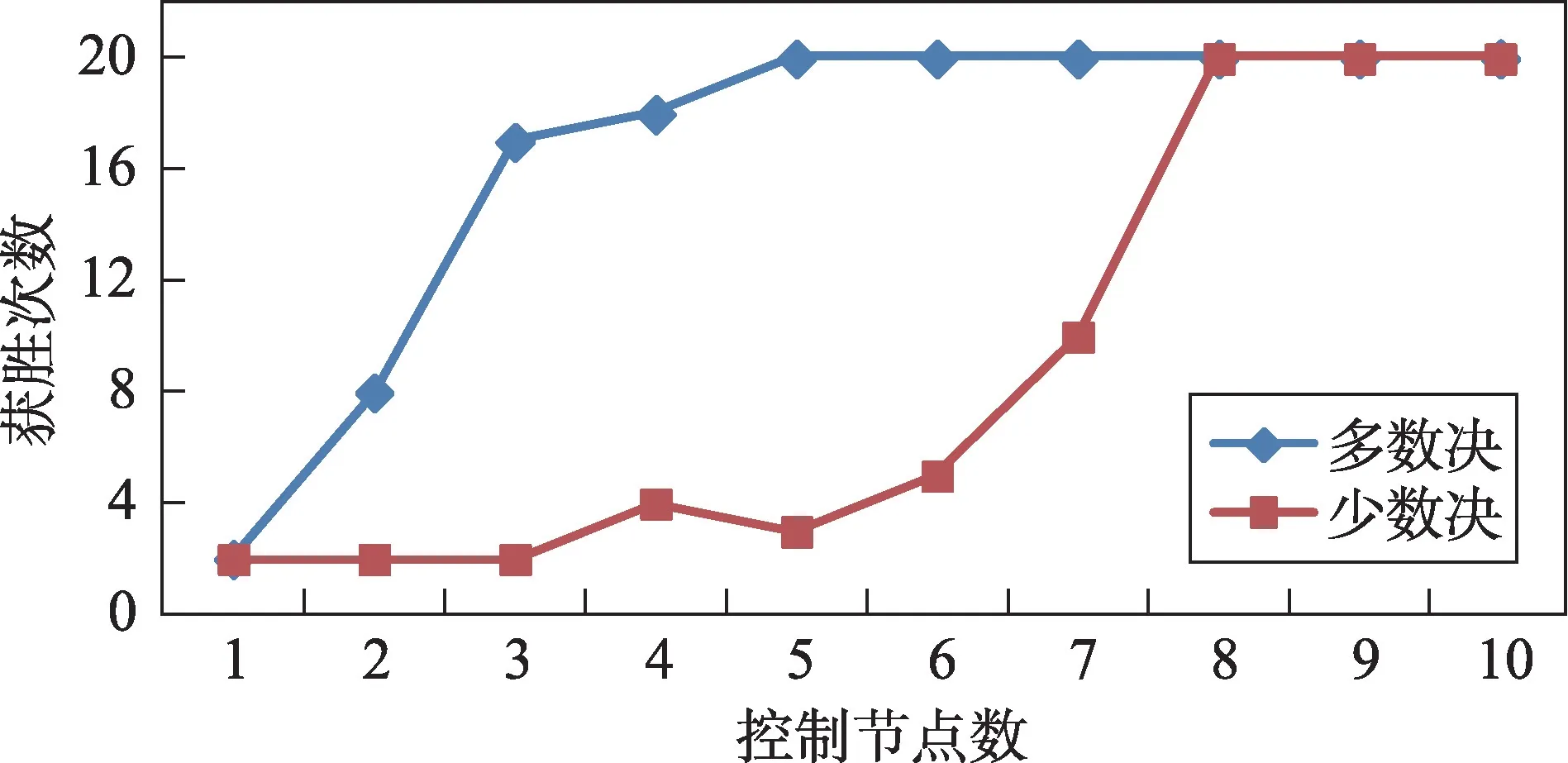
Fig.5 Comparison of election security of 10 cluster servers图5 10台集群服务器选举安全性对比
6.3 实验结果分析
(1)多数决选举机制和少数决选举机制在成功选举出Leader的所需时间基本一致。
(2)8台集群服务器时分别使用两种选举机制发起绝对控制攻击,少数决要比多数决多控制37.5%的节点才能确保攻击成功,即少数决选举安全性明显高于多数决选举。
(3)10台集群服务器分别使用两种选举机制发起绝对控制攻击,少数决要比多数决多控制30%的节点才能确保攻击成功,即在表1中的低值时,少数决选举安全性也远高于多数决选举。
(4)对比图4、图5两种选举机制的斜率,少数决选举只有在控制节点数临近绝对控制攻击满足条件时,才会对获胜次数产生明显影响;而多数决选举在随控制节点数增加的初始阶段,就对获胜次数产生明显的影响。
7 结束语
本文通过理论分析和实验证明,在分布式系统中采用少数决方式进行Leader节点选举是完全可行的,且少数决选举机制相比多数决选举机制在降低控票攻击风险方面有明显的优势。本文认为此种选举机制具有很好的科学性和进一步的研究价值。下一步,将研究分析少数决选举机制在其他领域的应用潜力。
