布谷鸟算法的收敛性分析及性能比较*

刘晓东，孙丽君，陈天飞+

1.河南工业大学粮食信息处理与控制教育部重点实验室，郑州 450001

2.河南工业大学郑州市机器感知与智能系统重点实验室，郑州 450001

3.河南工业大学电气工程学院，郑州 450001

4.河南工业大学信息科学与工程学院，郑州 450001

1 引言

近年来，群体智能算法广泛应用于各个领域，其通过团队的协作和组织，将简单的个体联系起来产生群体智慧，并以此解决实际问题[1]。与传统优化算法相比，群体智能算法有以下三种特点：灵活性、稳健性、自组织性[2]。这三种特点主要表现：若在可变系统或者环境下，群体适应能力强；当某个体出现状况时，不会影响群体对问题的处理；群体智能算法是通过个体相互竞争或者作用产生的，不受任何中心控制和局部监管[3]。

群体智能算法经过多年的发展，取得了许多重要的研究成果。例如，Eberhart和Kennedy观察鸟群、鱼群的行为于1995年提出了粒子群算法[4]（particle swarm optimization，PSO）。该算法具有收敛速度快、效率高的特点，但任子晖等人[5]从转移概率的角度证明了标准粒子群算法不是全局收敛的。同年，Storn和Price提出了差分进化算法（differential evolution，DE）[6]，它具有结构简单，易于实现等优点，广泛应用于模式识别、数据挖掘等领域。2005年，Karaboga小组通过观察蜜蜂群体行为得到启发，提出了人工蜂群算法（artificial bee colony，ABC）[7]，而孔翔宇等人[8]基于鞅论研究了人工蜂群算法的几乎必然强收敛性，并且由于该算法结构简单，易于实现，在电力、组合优化、系统工程等领域有着广泛的应用。2010年，Yang提出了蝙蝠算法（bat algorithm，BA）[9]，并且尚俊娜等人[10]采用Markov链模型证明了该算法具备全局收敛性。同样，该算法具备模型简单、参数少等优点，常常应用于组合优化等问题。2009年，Yang和Deb观察布谷鸟巢寄生育雏行为，结合莱维飞行特征，首次提出了布谷鸟搜索算法[11]（cuckoo search，CS）。该算法主要特点：参数少、操作简单、寻优能力强等。目前，布谷鸟算法在图像和信号处理、电力系统、医学应用、数据挖掘等领域已经得到成功应用[12-15]。例如Garg等[16]提出了CS算法的最优掩模生成方法，用于抑制噪声和语音信号的增强；Liu将CS算法应用于临床疾病诊断中等[17-19]。

自CS算法提出以来，一些学者对CS算法的性能进行了改进。这些改进的方式可大体分为三方面：（1）发现概率P的改进，如文献[20]认为被发现的概率P的选择会影响最优解的搜索；（2）步长的改进，如文献[21]针对优势解交换信息步长进行改进；（3）混合CS算法改进，如文献[22]介绍了一种和差分进化算法相结合的混合CS算法。除此之外，CS算法的变体及应用研究也有不错的成果，如文献[23]提出了一种离散二进制布谷鸟搜索算法来处理二进制优化问题；文献[24]提出了离散CS算法，用于解决带时间窗和同时取送货的车辆路径问题；文献[25]提出了混合多目标布谷鸟搜索算法来解决多目标优化问题。另外，CS算法在性能分析方面也有进步，如文献[26]使用模糊系统来动态调整CS算法的参数，分析了参数对CS算法性能的影响等。然而，这些改进算法仅仅在实验的角度下对比了算法收敛性能的提高，而缺乏必要的理论分析。因此，CS算法在实验和理论上的综合分析是必要的，进而为后期的改进提供支持。

本文对CS算法构建数学定义，并建立其Markov模型，在此基础上利用算法收敛准则证明布谷鸟的全局收敛性。虽然文献[27]同样采用Markov模型对CS算法进行了收敛性分析，但本文的收敛性证明与文献[27]存在着一定的差异。首先，在CS算法的数学定义方式上存在着显著不同；其次，本文对CS算法收敛性分析证明中采用了Chapman-Kolmogorov方程的方式进行证明和分析。本文不仅对已有CS算法的理论分析加以补充，而且使CS算法的收敛分析更加全面。然后，从两方面展开实验分析：（1）根据数据规模的变化来绘画出时间复杂度增长曲线，对比分析五种算法的复杂度。（2）五种典型群体智能算法在相同维度和不同维度情况下分别以数据统计的形式对同一个优化问题进行比较；并通过图像对比的形式直观地衡量算法的性能。

2 布谷鸟算法原理

在自然界中，布谷鸟的繁殖习性是比较独特的，它是巢寄生鸟类，巢寄生是指利用其他鸟类的巢穴来孵化自己的蛋[28]。若要提高蛋的存活率，则将宿主的蛋破坏掉或者伪装。若蛋被宿主发现，则宿主寻找新的鸟巢或者破坏蛋[29]。这个是自然选择的过程，选择鸟巢的好坏直接影响下一代的生存率。通过布谷鸟搜寻鸟巢的过程来模拟出布谷鸟算法，该算法基于三种理想规则：

规则1每只布谷鸟一次只能产一枚卵，并随机选择地放入一个鸟巢中。

规则2在随机选择的一组鸟巢中，最好的寄生巢将会被保留到下一代。

规则3鸟巢数量是固定的，被发现的概率Pa,Pa∈[0,1]，若宿主发现蛋，它会将蛋摧毁或者重新寻找新巢。

基于以上三种理想规则，布谷鸟寻找宿主鸟巢的位置和路径更新公式如下：

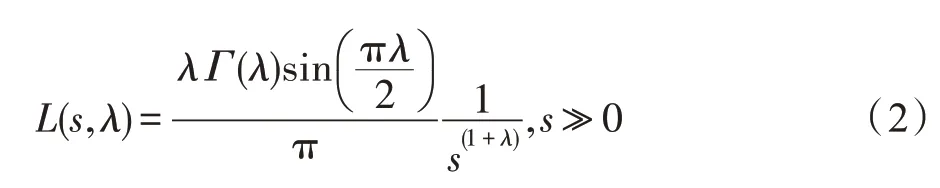
当鸟巢位置更新后，将区间[0,1]的随机数r与Pa比较，如果r＞Pa时，就随机更新一次鸟巢的位置，否则鸟巢的位置不变。

根据上述分析过程，布谷鸟搜索算法流程图如图1所示。

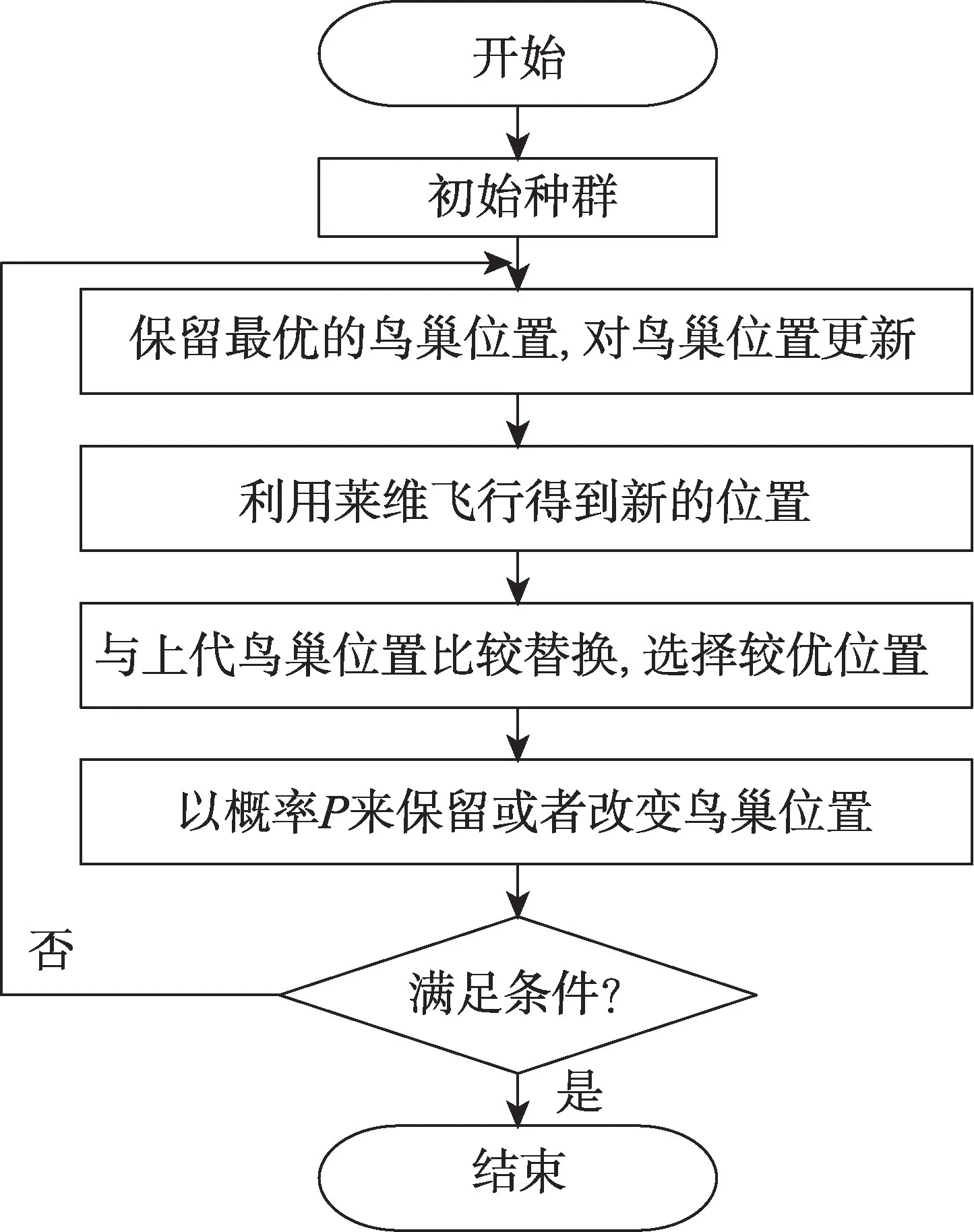
Fig.1 Cuckoo search flow chart图1 布谷鸟搜索算法流程图

3 Markov链收敛性分析

3.1 算法的收敛准则

收敛准则是一种判断算法收敛的理论分析方法，定理如下。

在Lebesgue测度空间定义搜索的下确界：

其中，v(x)表示在集合x上的Lebesgue测度。可以定义最优区域：

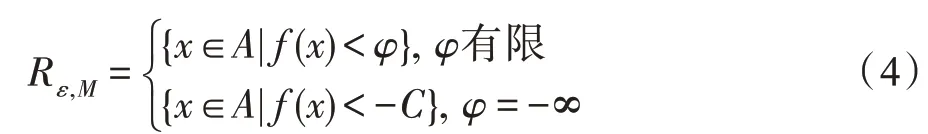
其中，ε＞0,C为充分大的正数，如果算法找到Rε,M中的一个点，则认为算法找到了可接受的最优值。

假设1f(D(x,ζ))≤f(x),若ζ∈A，则有f(D(x,ζ))≤f(ζ)。

假设2对于∀B∈A,s.t.v(B)＞0，有其中uk(B)为算法D第k次迭代搜索解在集合B上的概率测度。

定理1（算法全局收敛）设f是可测的，可测空间A是Rn上可测度的子集，算法D满足两个假设，是算法D产生的序列，则有，即算法全局收敛[30]。

3.2 CS算法的Markov链模型

定义1（鸟巢位置的状态和鸟巢位置的状态空间）鸟巢的位置构成布谷鸟的状态，记作x,x∈A,A为可行解空间。鸟巢位置的所有可能状态组成的集合构成鸟巢位置的状态空间，记为X={x|x∈A}。

定义2（鸟巢位置的群状态和鸟巢位置的群状态空间）鸟巢位置群中所有布谷鸟的状态构成布谷鸟巢位置群状态，记作S=(x1,x2,…,xN),其中xi表示第i个布谷鸟位置的状态。鸟巢位置群所有可能状态组成的集合构成鸟巢位置群的状态空间，记为S={s=(x1,x2,…,xN)|xi∈X,1 ≤i≤N}。

定义3（鸟巢位置的状态转移）对∀xi∈s，∀xj∈s，在CS算法迭代中，鸟巢位置的状态从xi转移到xj，记为T(xi)=xj。

定理2在CS算法中，鸟巢位置状态从xi转移到xj的转移概率P(T(xi)=xj)。其表达式为P(T(xi)=xj)=,其中是通过CS算法中式（1）位置转移的概率，表示被宿主发现概率所产生的位置转移概率。

证明假设鸟巢位置的状态从xi转移到xj过程中，它们之间有一次的中间转移状态xi′，此时P(T(xi)=xj)的概率为：

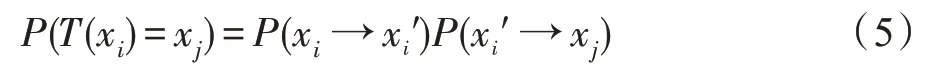
由于x、g是多维数据，加减号表示矢量加减，式（6）中绝对值表示超空间立方体的体积。

由布谷鸟算法的理想规则3可知，随机数r∈[0,1]与Pa对比。则鸟巢位置状态由xi′→xj的概率为：

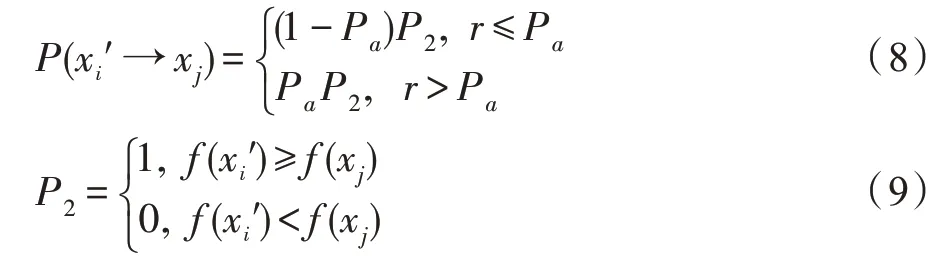
由此，定理得证。□

定义4（鸟巢位置的群状态转移）在布谷鸟算法迭代中，对于∀si=(xi1,xi2,…,xiN)∈S，∀sj=(xj1,xj2,…,xjN)∈S，鸟巢位置的群体状态从si转移到sj，记作T(si)=sj。

定理3在CS算法中，鸟巢位置的群状态从si转移到sj的转移概率为：

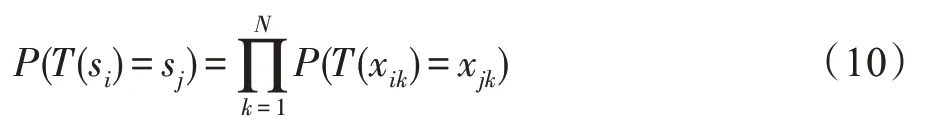
证明鸟巢位置的群状态中包含所有鸟巢位置的状态。当鸟巢位置的群状态从si转移到sj时，表示群状态的所有位置状态都会同时转移，即T(xi1)=xj1,T(xi2)=xj2,…,T(xiN)=xjN同时成立，则鸟巢位置群状态转移的概率为：

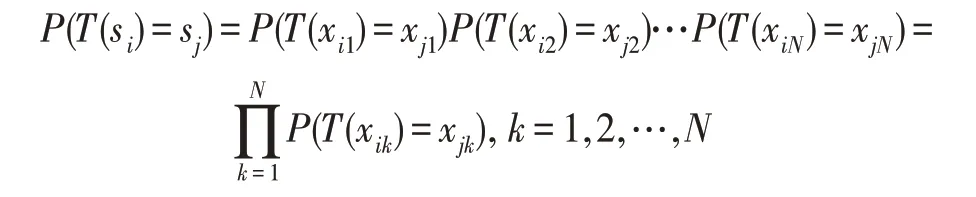
由此，定理得证。□

定理4CS算法中鸟巢的群体状态序列{s(t):t≥0}，是有限齐次Markov链。

证明任何优化算法的搜索空间都是有限的，任一个鸟巢的位置状态xi都是有限的，因此鸟巢位置的状态空间X也是有限的。群状态空间s=(x1,x2,…,xN)由N个鸟巢位置组成，N为有限正整数，则鸟巢位置群状态空间S也是有限的。

由定理3得，群状态序列{s(t):t≥0}中，对于∀s(t-1)∈S,∀s(t)∈S,其转移概率P(T(s(t-1))=s(t))是由鸟巢群体中的所有鸟巢位置的转移概率P(T(x(t-1))=x(t))决定，由定理2可知，转移概率P(T(x(t-1))=x(t))仅与t-1时刻的状态x、优化问题的最大值和最小值相关，因此P(T(s(t-1))=s(t))也仅与t-1时刻的状态相关，而与时间t-1无关，即鸟巢的群体状态{s(t):t≥0}有Markov性和齐次性，又因为状态空间为可列集，所以其构成一个有限齐次Markov链。□

3.3 布谷鸟算法的收敛性分析

定义5设优化问题全局最优解g*，定义鸟巢位置的最优状态集M={s*=(x)|f(x)=f(g*),s∈S}。

定理5CS算法中，对鸟巢位置的状态序列{s(t):t≥0}而言，最优状态集M是状态空间S上一个闭集。

证明对∀si∈M∀sj∉M，对于任意转移步长l，l≥1，由Chapman-Kolmogorov方程可得：

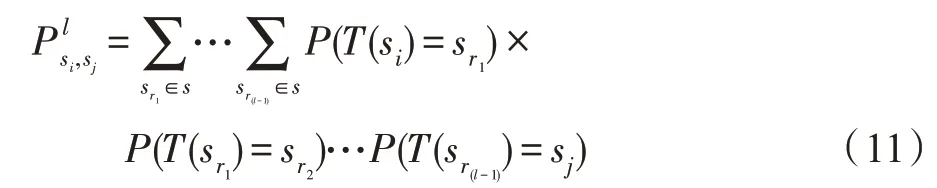
由sr(c-1)∈M,src∉M，有f(xc)＞f(xc-1)=f(g*)=inf(f(a))，a∈A，则至少存在，此时，因此M是S上的一个闭集。□

定理6鸟巢位置群体状态空间S，不存在非空闭集B,使得B⋂M=∅。

证明（反证法）假设群体状态空间S中存在非空闭集B，且B⋂M=∅，则设si=(g*,g*,…,g*)∈M，∀sj=(xj1,xj2,…,xjN)∈B,有f(xjc)＞f(g*)，由定理2和定理3可得，每个P(T(sj)=si)都有由于，则P(T(xj)=xi)≠0，因此B不是闭集，这与假设矛盾。因此鸟巢位置群状态空间S中不存在M之外的非空闭集。□

定理7假定Markov链有一个非空闭集E，且不存在另一个非空闭集D，使得E⋂D=∅，则当j∈E时，有且当j∉E时，有=0[31]。

定理8当群体内部迭代趋于无穷时，群体状态序列必将进入最优状态集M。

证明由定理5、定理6和定理7可证。□

定理9CS算法收敛到全局最优。

证明由于CS算法的适应度函数是非递增的，因此CS算法满足随机算法假设1。由定理8可知，CS算法满足假设2，故CS算法收敛于全局最优。□

4 CS算法的仿真实验分析

4.1 硬件设备和算法参数设置

实验是在操作系统为Windows 10，处理器是英特尔i5-8 400，固态硬盘256 GB和GTX1050的显卡的硬件环境下，采用Matlab2013运行算法，然后收集数据和图像。为了保障算法的正常运行，分别对5种不同的算法进行参数的调整，如表1所示，可以看出布谷鸟算法与其他算法相比，参数明显较少。

4.2 算法性能分析

4.2.1 复杂度分析

图2是5种典型智能算法运行时间对比图。根据复杂度的定义和算法伪代码可知，智能算法的计算规模均与种群的数目N、维度D和迭代次数有关，当维度和迭代的次数一样时，改变种群的数量即改变了计算的规模。本实验对表2中F1函数进行求解，绘制出5种典型群体智能算法的运行时间。从整体变化中可以看出5种群体智能算法的复杂度由高到低依次为ABC ＞DE ＞CS ＞PSO ＞BA 。总体来说，CS算法与其他算法相比复杂度较低。

Table 1 Algorithm parameter settings表1 算法参数设置

Fig.2 Time complexity comparison图2 时间复杂度对比

4.2.2 收敛性分析

收敛性分析包含了对算法的收敛速度、收敛精度及其局部搜索和全局搜索的分析。本部分实验是在Matlab2013软件平台上，对表2中18个测试函数进行求解，统计收敛数据并比较5种典型群体智能算法的性能，结果如表3和表4所示。

当判断条件（精度或迭代次数）不变时，将表2中测试函数独立运行50次，统计出均值、标准差和排名。其中，平均值和标准差分别代表着算法的搜索精度和稳定性。

CS算法在搜索精度上的比较分析，从表3中可以看出，当维度为10时，CS算法的平均排名在1.88，最终排名为第二位。在大部分测试函数上，CS算法的性能都优于其他算法，例如在F3、F4、F5等函数上，CS算法性能处于优势；并在F1、F2、F6等测试函数上算法性能相当；只有在F13函数上性能处于劣势。由表4看出，当维度为50时，CS算法的平均排名在1.61，最终排名处于第一。在所有测试函数中，除了F9、F10、F15函数CS算法性能处于中等，在其他函数上，CS算法的搜索性能都优于其他算法。此外，相同算法处理相同的问题时，当维度升高时，算法的搜索性能逐渐变差。根据表3和表4观察到CS算法在平均排名和最终排名都发生了变化，高维度时，CS算法性能表现得更为优秀。

Table 2 Test functions表2 测试函数

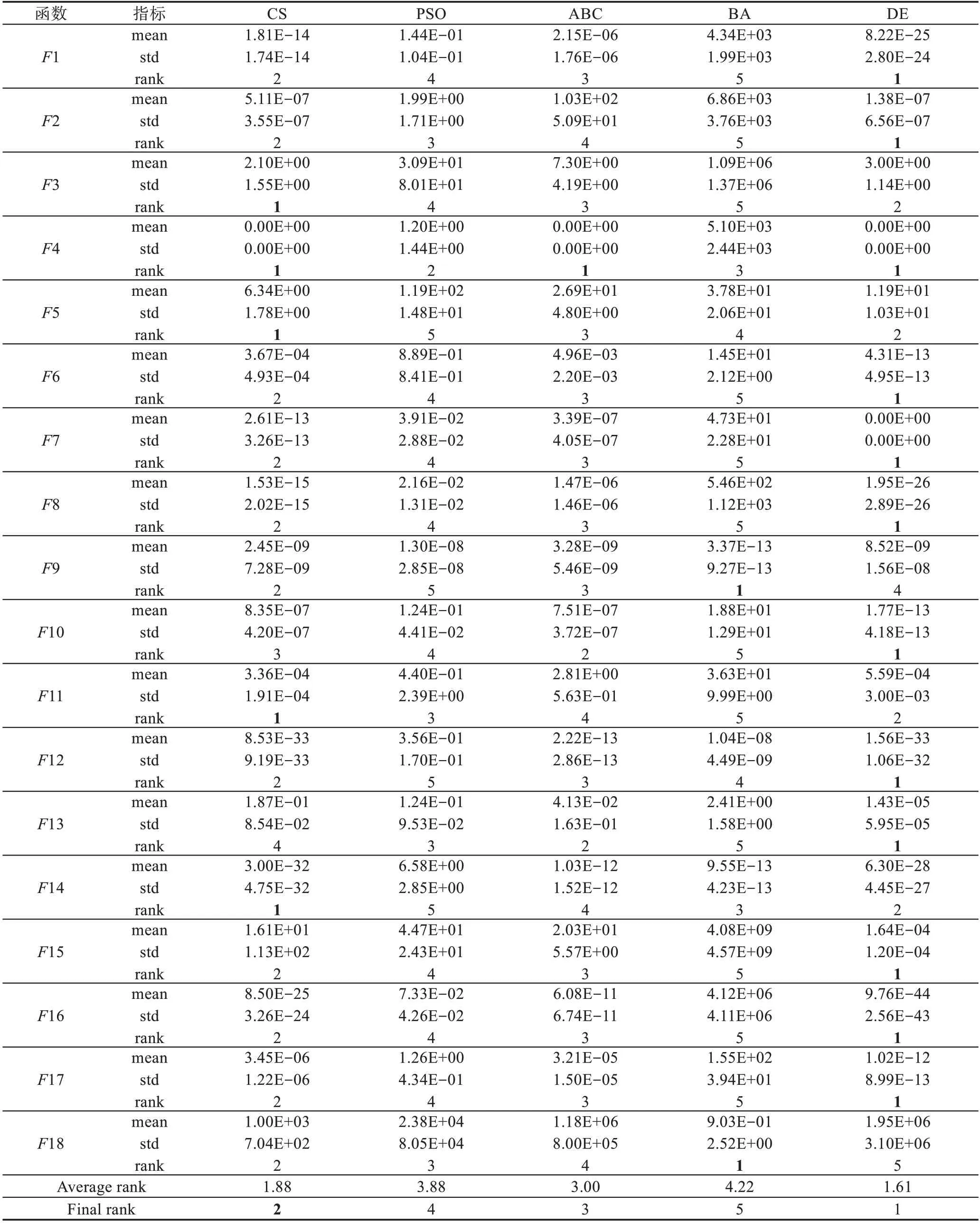
Table 3 Comparison of standard test functions(D=10)表3 标准测试函数的比较(D=10)

Table 4 Comparison of standard test functions(D=50)表4 标准测试函数的比较(D=50)

为了更加直观地评价5种算法的性能，首先选取18种标准测试函数分别对5种算法独立运行50次，并画出平均进化过程的结果图像，如图3～图20所示。其次将测试函数分为单峰测试函数和多峰测试函数。单峰测试有F1、F2、F4、F8、F10、F11、F12、F14、F16、F17。单峰测试函数检测出算法的寻优的精度、寻优的速度。多峰测试函数有F3、F5、F6、F7、F9、F13、F15、F18，由于多峰测试函数存在许多极值，因此多峰测试函数的作用为测试出算法是否会陷入局部最优以及全局最优的搜索能力。

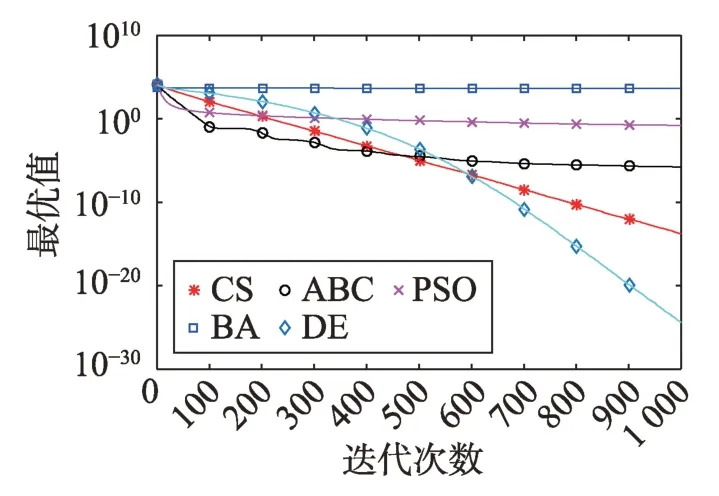
Fig.3 Logarithm F1 curve图3 F1对数曲线

Fig.4 Logarithm F2 curve图4 F2对数曲线

Fig.5 Logarithm F3 curve图5 F3对数曲线

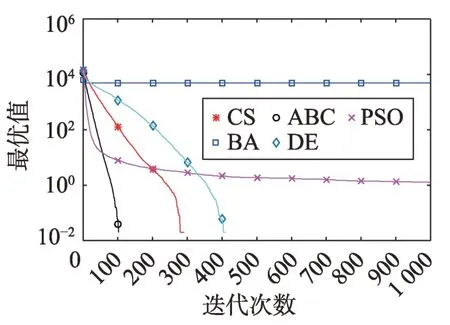
Fig.6 Logarithm F4 curve图6 F4对数曲线

Fig.7 Logarithm F5 curve图7 F5对数曲线

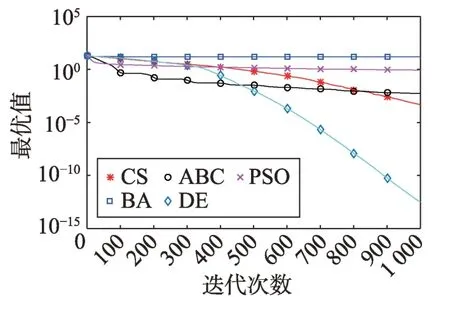
Fig.8 Logarithm F6 curve图8 F6对数曲线

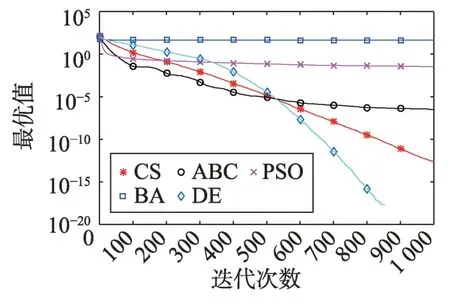
Fig.9 Logarithm F7 curve图9 F7对数曲线

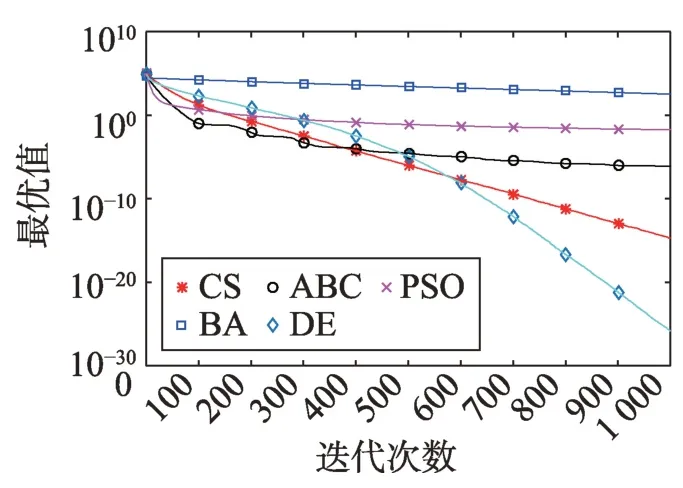
Fig.10 Logarithm F8 curve图10 F8对数曲线

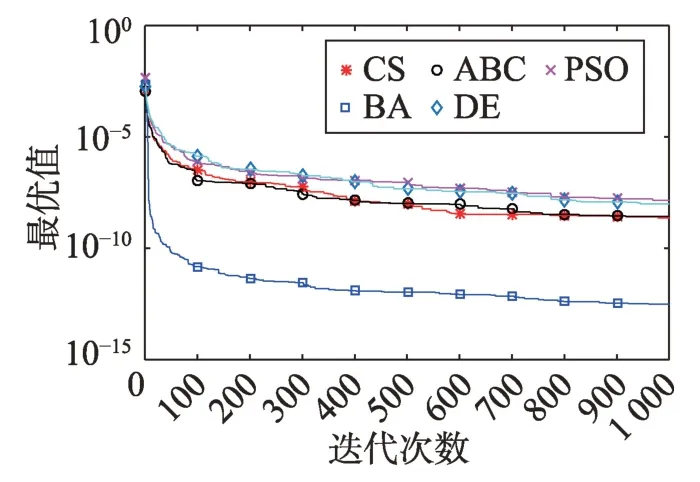
Fig.11 Logarithm F9 curve图11 F9对数曲线

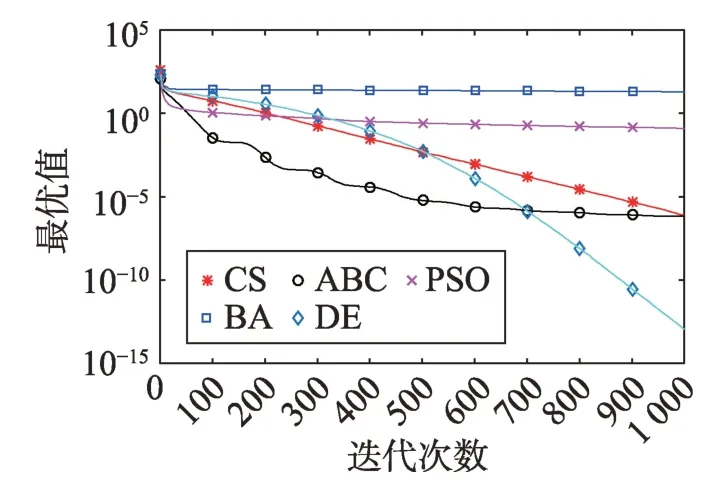
Fig.12 Logarithm F10 curve图12 F10对数曲线

Fig.13 Logarithm F11 curve图13 F11对数曲线

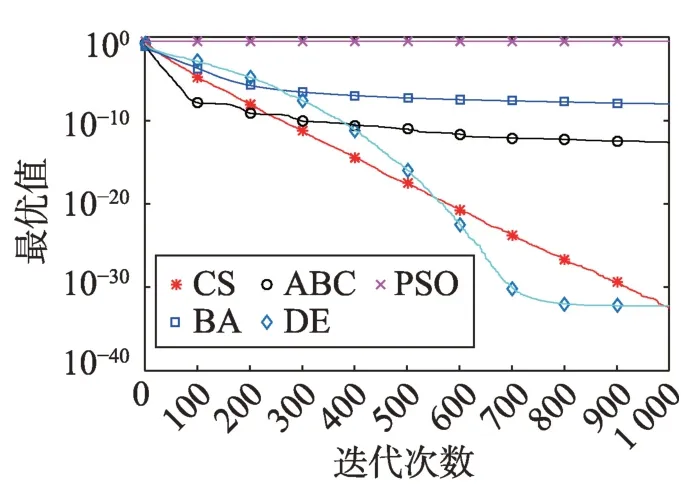
Fig.14 Logarithm F12 curve图14 F12对数曲线

Fig.15 Logarithm F13 curve图15 F13对数曲线

Fig.16 Logarithm F14 curve图16 F14对数曲线

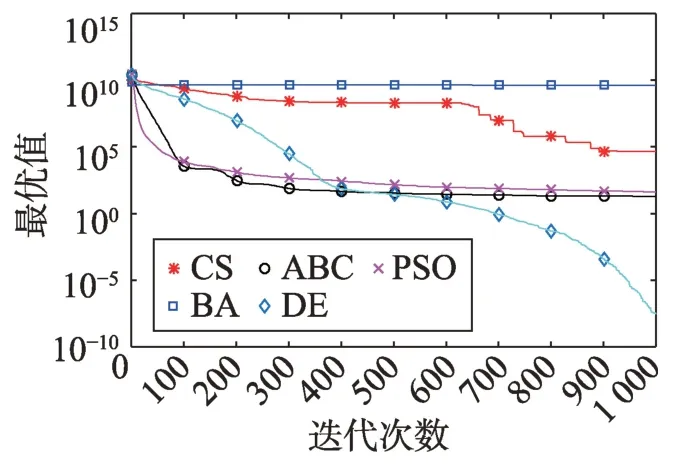
Fig.17 Logarithm F15 curve图17 F15对数曲线

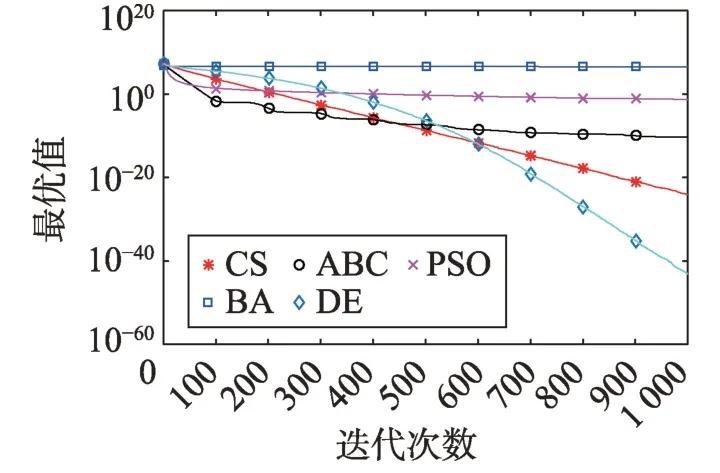
Fig.18 Logarithm F16 curve图18 F16对数曲线

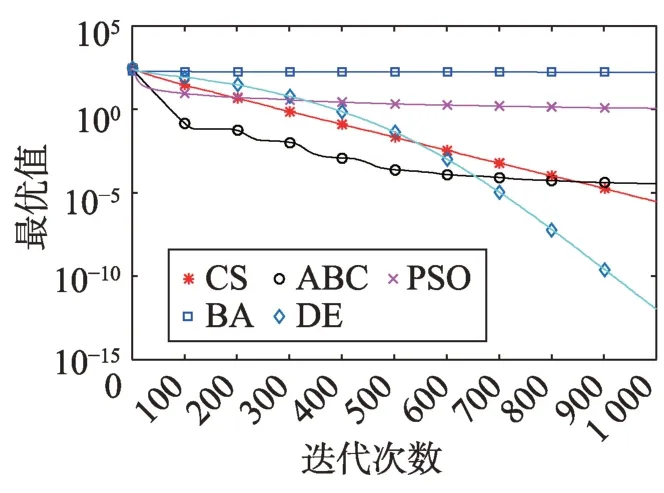
Fig.19 Logarithm F17 curve图19 F17对数曲线

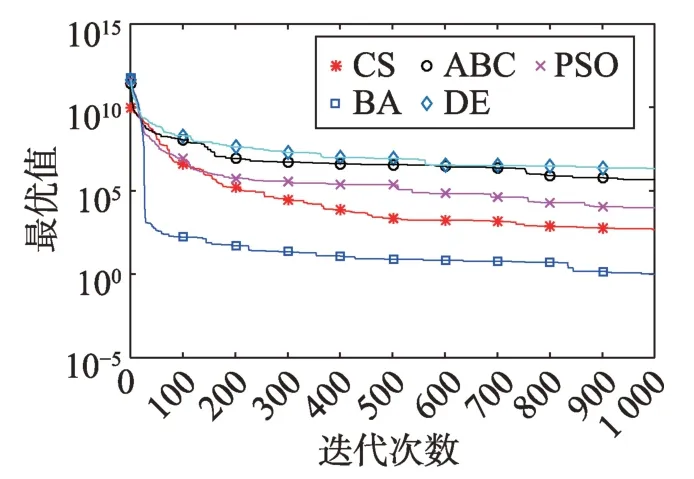
Fig.20 Logarithm F18 curve图20 F18对数曲线

观察单峰函数曲线图3、图4、图10、图12、图14、图18、图19可知5种算法在搜索精度上CS算法始终处于优势。如图6观察出CS、DE、ABC都达到了函数理论值，如图13、图16观察出CS算法的计算精确度最高。

观察多峰曲线图5、图7、图8、图9、图15可以看出，ABC算法出现几次陷入局部最优值的变化，人工蜂群算法是通过蜜蜂之间的正反馈机制，加快了全局寻优，但在接近全局最优时，寻优的速度变慢，种群的种类变少。CS算法曲线近似光滑的曲线，CS算法在处理这一类问题时，很好地跳出了局部最优值，使其尽可能快地搜寻全局最优值。如图11、图17、图20中5种算法曲线都出现了局部最优值，由于CS算法在个体和群体之间的平衡，使得CS算法更好地跳出局部最优值。从图11可以看出，CS算法和ABC算法的曲线极为相似，它们的局部搜索能力比较强，并能够更好地跳出局部最优值，PSO算法对数曲线收敛速度最快，但从整体看精度不如其他算法，也容易陷入局部极值，粒子群是以全局最优粒子进行搜索，粒子缺乏多样性。如图17、图20中CS算法曲线出现了几次局部最优值的变化，最终停留到局部最优值。总体来说，无论是处理单峰函数问题还是处理多峰函数问题时，CS算法的性能都优于其他算法，CS算法的局部搜索和全局搜索能力较强，但在处理某些问题时，也会陷入局部最优的情况。

5 结束语

本文对布谷鸟算法从两方面展开分析：（1）理论分析，先对CS算法构建数学定义，再利用数学定义构建Markov模型。然后，利用算法收敛准则证明布谷鸟的全局收敛性。（2）实验分析，统计5种算法分别在不同维度下解决单峰问题和多峰问题的平均值、标准差。观察得出当维度升高时，优化算法性能逐渐变差。再通过图表的形式，分析出布谷鸟算法复杂度和性能。CS算法与其他算法相比，其精度较高、复杂度较低、稳定性较好，但在收敛速度方面明显弱于粒子群算法和蝙蝠算法。若能够对CS算法的性能进行深入的探究，将会使CS算法的发展更进一步。