声速剖面主导的浅海声传播最佳深度规律研究

2020-10-15窦雨芮周其斗纪刚刘文玺

中国舰船研究 2020年5期

窦雨芮，周其斗，纪刚，刘文玺

海军工程大学舰船与海洋学院，湖北武汉 430033

0 引言

近年来，水声学研究的重点逐渐从深海转到浅海，我国沿海海域多为浅海，研究浅海声场声学特性无论是从军事战略的角度，还是经济发展的角度考虑，都有其重要作用[1]。如何更好、更高效地在浅海进行声呐探测和水声通信一直是水声界关注的焦点，也是实际应用上的难题。浅海的波导声学特性相对于深海更加复杂。波导的上、下界面分别受海面和海底边界条件的制约，由于边界条件不同，声能量在深度方向上的分布并不均匀，当传播距离一定时，不同深度的声能量差异可达20 dB。因此，接收点位置的选取对声信号接收效果的影响很大，如何更好地选择接收点深度以最大程度地提高声学探测和水声通信能力就显得十分重要。

在给定声源位置的情况下，垂直方向的声传播损失最小点被称为最佳深度。最佳深度的选取可以优化接收效果，如被动声呐放置在最佳深度可以提高目标探测的概率。国内外学者针对最佳深度做了一定的研究。Weston[2-3]首先对声场的平均声强进行了研究，通过计算等声速梯度条件下深度方向上的距离平均声强，发现了最佳深度现象，并用声强解释了该现象形成的原因。而后，Gershfeld 等[4]通过对声传播损失和信噪比的计算，得出浅海声传播的最佳深度与声源点深度相同的结论，并研究了声源位置、海底类型和声源频率对最佳深度的影响。以上都是针对给定声源情况而计算的最佳深度。Ferla 等[5]通过计算声呐的检测半径，对声源深度未知时的最佳深度位置进行了研究，得出在声源深度未知时，接收点深度选择在声速最小处时接收效果最佳的结论。王晓宇等[6]分别对理想Pekeris 波导和实际浅海分层波导下的水平线列阵最佳布放深度进行研究，得出了最佳布放深度应与声源深度相同的结论。范培勤等[7]通过将深度方向的声传播损失转化为检测概率，研究了声呐最优工作深度、正梯度和负梯度声速剖面下的最佳深度，得出声呐应放置在声速较小深度的结论。

现有的研究大多只针对等声速梯度情况下的声传播最佳深度现象，有关声速剖面对最佳深度影响的研究则十分有限，且相关研究选取的声速剖面类型也较少，没有系统、全面地研究其对最佳深度的影响。在进行实际的水声通信时，声速剖面对远距离声传播的影响不可忽视，且不同类型的声速剖面对声传播的影响不同。

本文将基于实际浅海不同季节的典型声速剖面，运用简正波方法，计算声传播损失随距离和深度变化的伪彩图，研究不同声速剖面下的最佳深度位置，较为全面地总结声速剖面在低频和高频时对最佳深度的影响规律，以为更好地运用最佳深度规律进行水声探测和通信提供一定帮助。

1 理论公式

浅海声传播问题可以近似采用单位强度的点声源在水平均匀的分层波导中的响应来模拟，任意一点的声压 p满足如下波动方程：

运用模式函数的正交性，得到

式（12）所示的传播损失是基于不同模态简正波之间相位叠加的结果，如果忽略简正波之间的相位差异，只考虑简正波携带的能量多少，通过这种方式叠加会产生非相干声传播损失TLInc。Jensen[8]通过对比不同模态简正波的非相干叠加与1/3 倍频程平均后的传播损失实地测量结果，发现非相干叠加的声传播损失计算结果和1/3 倍频程平均后的测量结果一致，说明非相干叠加的计算结果在描述传播规律时可以代替相干叠加。非相干损失可以清楚地显示声场的能量分布，本文采用TLInc随距离和深度的变化来描述声场，其非相干传播损失的计算公式如下：

2 声速剖面的形成和典型结构

海水声速是研究声传播的基本物理量，是声场分析中不可或缺的一个重要参数，其在海洋测距和参数反演等方面都有重要应用。由于海水中介质分布不均匀，声速在深度方向的分布也不均匀，从而形成了不同类型的声速剖面，其存在对远场声传播的影响很大[10-11]。本节将主要介绍声速剖面的形成及其典型结构，以为后续研究提出可采用的声速剖面模型。

2.1 声速剖面的形成

海水中声速是影响声传播的一个重要因素，其通常与密度和压缩系数有关。在海水中，密度和压缩系数是温度、盐度和静压力的函数，而静压力又与深度有关，所以海水中声速也是温度、盐度和深度的函数[12]。自20 世纪50 年代以来，许多学者[13-14]针对海水声速的经验函数进行了大量研究，对不同情况下的声速经验公式进行了总结。本文选取的是简化后的声速经验公式[15]，在一般情况下，该经验公式可以较为准确地预测声速值。

2.2 声速剖面的典型结构

浅海海域的声速剖面受多种因素的共同作用，其中温度是影响剖面类型的主要因素。声速剖面的变化总体遵循一定的季节规律，如浅海表层水温在夏季和冬季将分别出现升高或降低的现象，其声速也随之增大或减小。图1 所示为我国黄海、渤海附近不同季节的典型声速剖面[16-17]。

基于图1 所示不同季节的声速剖面图，下面对其形成原因进行解释：在冬季，黄海、渤海附近的部分海域由于受到强对流混合作用的影响，海水温度随深度的变化不大，声速只与海水深度有关，将随深度的增大而增大，出现图1（d）中红色短线D2 所示的微弱的正梯度现象；而受到弱对流影响的海域温度则随深度的增加缓慢减小，声速随深度的变化很小，出现图1（d）中黑色实线D1 所示的等梯度现象。当由冬季过渡到春季时，等梯度和正梯度现象逐渐消失，海水层表面由于光照和风力波浪的搅拌作用，会出现厚度约10 m的混合层，该混合层的温度不变，声速梯度为等梯度，海水较深处的组成成分较为稳定，温度较低且为常数；混合层与海水较深处的等温层间过渡区为温跃层，该区域温度会随着深度的增加而减小，声速也随着深度的增加而减小，其声速梯度如图1（a）中黑色实线A1 所示，由于地理位置的不同，部分海域的温跃层尚未形成，其声速梯度如红色短线A2 所示。到了夏季，海面受到强烈的阳光照射，表层温度会急剧增大，海水较深处的温度则基本不变，此时跃层强度达到最大，形成了强度较大的负跃层B1 和负梯度B2（图1（b））。秋季，海水的混合层厚度逐渐增加，温跃层向下移动，会形成如图1（c）所示的不同位置的负跃层梯度。

3 声速剖面影响下的最佳深度研究

2.2 节给出了我国浅海海域的典型声速剖面。本节将基于浅海声场模型，运用简正波方法，根据给出的不同季节的声速剖面，计算非相干声传播损失随距离和深度变化的伪彩图，然后再通过观察伪彩图，得到声传播的最佳深度，并研究声速剖面变化对最佳深度的影响。

3.1 计算模型

选取渤海附近海域进行模拟，海水深度z=100 m，海面设置为压力释放边界，半无限弹性海底表面平坦，底质为泥底，其参数如表1 所示，海水、海底密度和声速水平均匀不变。由于要考虑不同的声源位置对最佳深度的影响，在设置声源位置时，应选取海水层中有代表性的点，本文选取声源深度zs=10，50 和90 m，分别模拟近海面、海水中层和近海底处的点声源。根据文献[18]的经验，设置水平距离为80 km，在该距离内，声传播损失伪彩图涵盖了近场和远场的大部分声场特征，且范围以外的传播损失较大，潜艇的辐射噪声在该距离外已低于海洋环境噪声。图2 给出了声源深度zs=50 m 时的声场计算模型。

3.2 声速剖面对最佳深度的影响

声速剖面对声传播的影响可以通过声传播损失随距离和深度变化的伪彩图来体现。通过将模型内每点的坐标（r, z）代入式（13），可得到整个模型的非相干声传播损失，传播损失相同的点用同一颜色代替，就可得到声场的传播损失伪彩图。

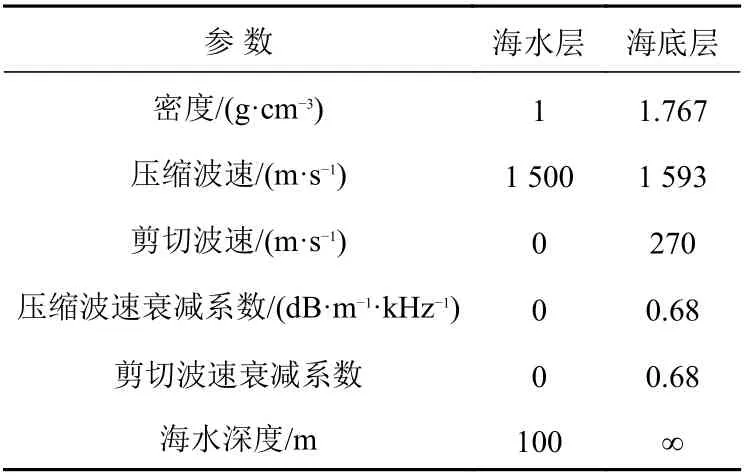
表1 声场的模型参数Table 1 Model parameters of acoustic field

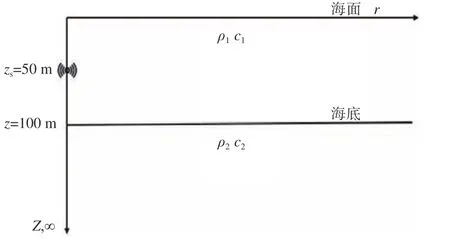
图2 浅海声场计算模型Fig. 2 Calculation model for shallow water acoustic

本节选取4 种典型的声速剖面：等梯度、负梯度、正梯度和负跃层，分别计算其声传播损失伪彩图，研究声速剖面变化对最佳深度的影响。

3.2.1 等梯度声速剖面对最佳深度的影响

选取图1 中的等梯度声速剖面D1，选取声源深度zs=10，50 和90 m，点声源频率Freq=50 和300 Hz（分别代表低频和高频），得到声传播损失伪彩图如图3 所示。

图3 中柱状图从上至下颜色由红至蓝变化表示声传播损失不断增大，每一点的声传播损失值均可从柱状图中对应的颜色得出。从图3 中可以看出：

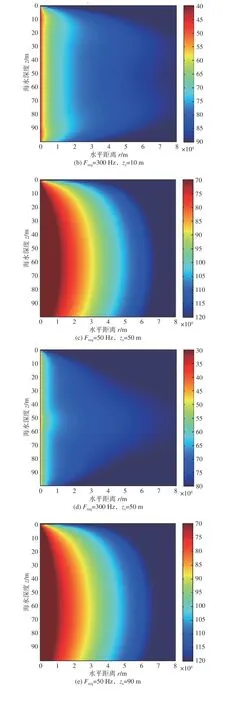
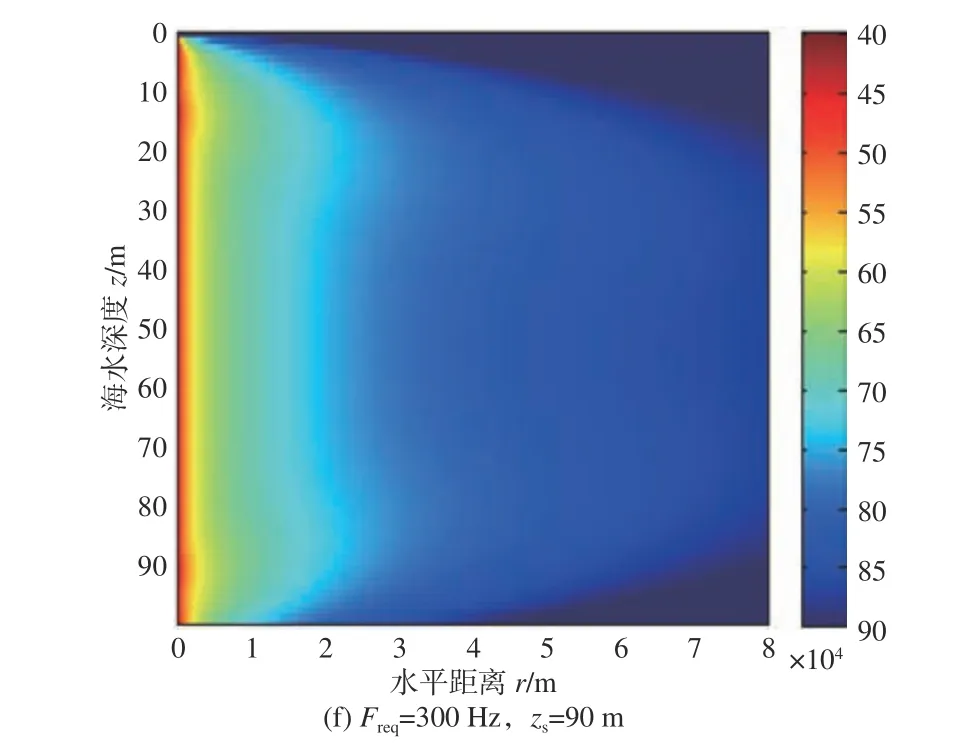
图3 等梯度下声源深度zs =10，50 和90 m 时不同频率的声传播损失伪彩图Fig. 3 Transmission loss versus depth and range for fixed sources at 10，50 and 90 m with different source frequencies for constant gradient

1）当声源频率Freq=50 Hz 时，声源深度zs=10，50 和90 m 时的声场传播损失随距离和深度变化的图相似。在深度方向上，声传播损失随着深度的增大先减小后增大，声传播的最佳深度均位于海水层中部附近。最佳深度位置不随声源深度改变是因为低频点声源激发声场中的简正波个数较少，少数阶简正波叠加后的位移幅值最大处位于海水中层偏下，即该位置处的能量最大，声传播损失最小，故形成最佳深度。

2）当声源频率Freq=300 Hz 时，声场的传播损失在垂直方向上近似关于H/2 对称。在近场时，10 m和90 m 处点声源激发的声场在声源深度和声源的对称深度出现了最佳深度现象，在传播到远场的过程中，最佳深度从声源深度和其对称深度向中间移动。这是由于高频点声源激发的声场简正波个数较多，不同阶简正波的量级不同，简正波的量级与该阶简正波在声源深度处的幅度成正比，即简正波在声源深度处的幅度越大，简正波的量级就越大，所以简正波叠加后的声场最佳深度位于声源深度。最佳深度总是成对出现的原因在于在等梯度声速剖面下，简正波的位移幅值在深度方向上近似关于H/2 对称，所以声源的对称深度也是最佳深度。最佳深度的位置在水平方向上发生变化是因为声能量在传播过程中不断衰减，简正波个数逐渐减少，导致最佳深度向中间移动。

3.2.2 负梯度声速剖面对最佳深度的影响

选取图1 中负梯度声速剖面A2，在相同条件下计算不同声源位置和不同频率下的声传播损失，结果如图4 所示。

由图4 可以看出：当频率Freq=50 Hz 时，声场的最佳深度与声源深度无关，最佳深度位于海水层中部附近；当频率Freq=300 Hz 时，由于声速剖面的存在，声场的最佳深度只位于声源深度，这同样是由于简正波叠加所造成的，随着声源位置的下降，声场的传播损失越来越小，最佳深度的现象越来越明显，即声源放置在声速梯度较小的位置时最佳深度现象最明显。这是由于声速较小处点声源发出的声线在传播过程中其弯曲程度比声速较大处声源发出的声线弯曲程度大，很多声线在还没有到达海面时就已发生转向，导致声能量较多地集中在海水层下方，又因为声源深度处位移幅值大的简正波量级也很大，故使得此时的最佳深度现象最为明显。

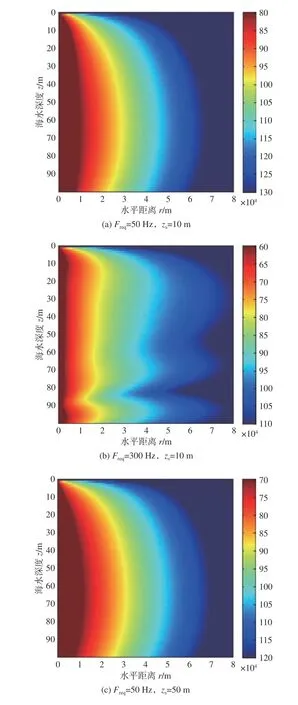
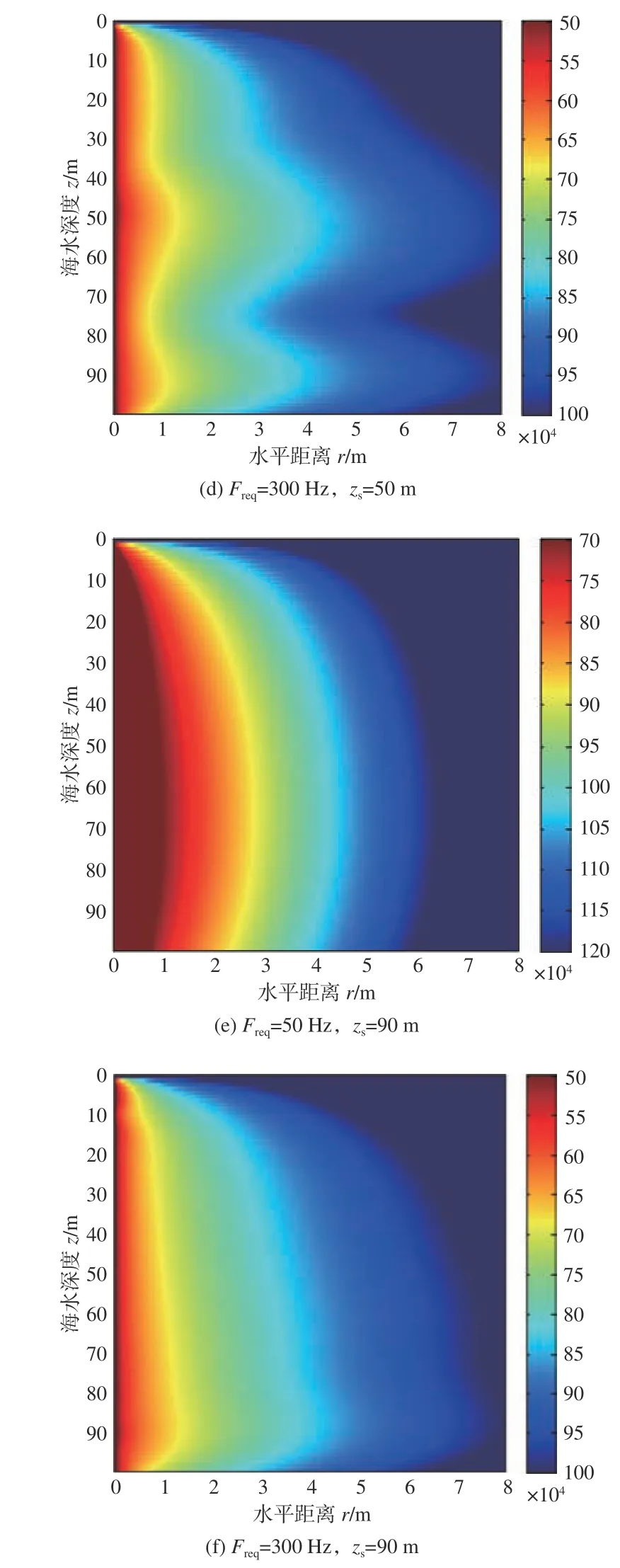
图4 负梯度下声源深度zs =10，50 和90 m 时不同频率的声传播损失伪彩图Fig. 4 Transmission loss versus depth and range for fixed sources at 10，50 and 90 m with different source frequencies for negative gradient

3.2.3 正梯度声速剖面对最佳深度的影响

选取图1 中正梯度声速剖面D2，给出不同声源位置在低频和高频的声传播损失如图5 所示。

从图5 中可以看出：当频率Freq=50 Hz 时，声场的最佳深度同样位于海水层中部附近；当频率Freq=300 Hz 时，声源在声速梯度较小处时同样展示了最为明显的最佳深度现象和最小声传播损失，其原因与负梯度情况下的相同。

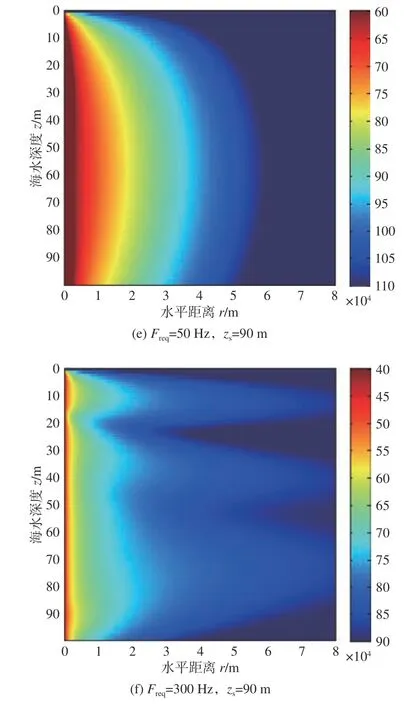
图5 正梯度下声源深度zs =10，50 和90 m 时不同频率的声传播损失伪彩图Fig. 5 Transmission loss versus depth and range for fixed sources at 10，50，and 90 m with different source frequencies for positive gradient

3.2.4 负跃层声速剖面对最佳深度的影响

等梯度、负梯度和正梯度条件下的声速梯度随海水深度保持不变，而由于温跃层的存在，负跃层的声速梯度在深度方向发生了变化，这种变化使得负跃层声速剖面对最佳深度的影响较为复杂。为系统、全面地研究负跃层声速剖面下最佳深度变化规律，本节考虑了由季节更替引起的温跃层位置变化对最佳深度的影响。

为研究负跃层声速剖面下温跃层位置对最佳深度的影响，选取春季和秋季的负跃层声速剖面A1，C1 和C2（分别代表厚度为20 m 的温跃层位于海面下10，20 和30 m 处），点声源深度同样选取为10，50 和90 m。由于负梯度下低频点声源的最佳深度特性较为稳定，而负跃层是负梯度的一种特例，所以很容易地可以得出低频时负跃层下的最佳深度同样位于海水层中层附近。本节只研究高频时的最佳深度变化规律，选取声源频率Freq=300 和500 Hz，计算得到声源深度zs=10，50，90 m 时不同温跃层位置的声传播损失伪彩图如图6 所示。

图6 给出了声源深度zs=10 m，频率Freq=300和500 Hz 时不同温跃层位置的声传播损失伪彩图。由图中可以看出，随着温跃层逐渐向下移动，温跃层上层的混合层厚度增大，声场的最佳深度始终位于混合层内声源深度附近，且最佳深度现象越来越明显，混合层下方的声传播损失在深度方向上的振荡越来越剧烈。由图中还可以看出，随着频率的增大，最佳频率现象越来越明显，混合层下方的振荡现象也越来越剧烈。

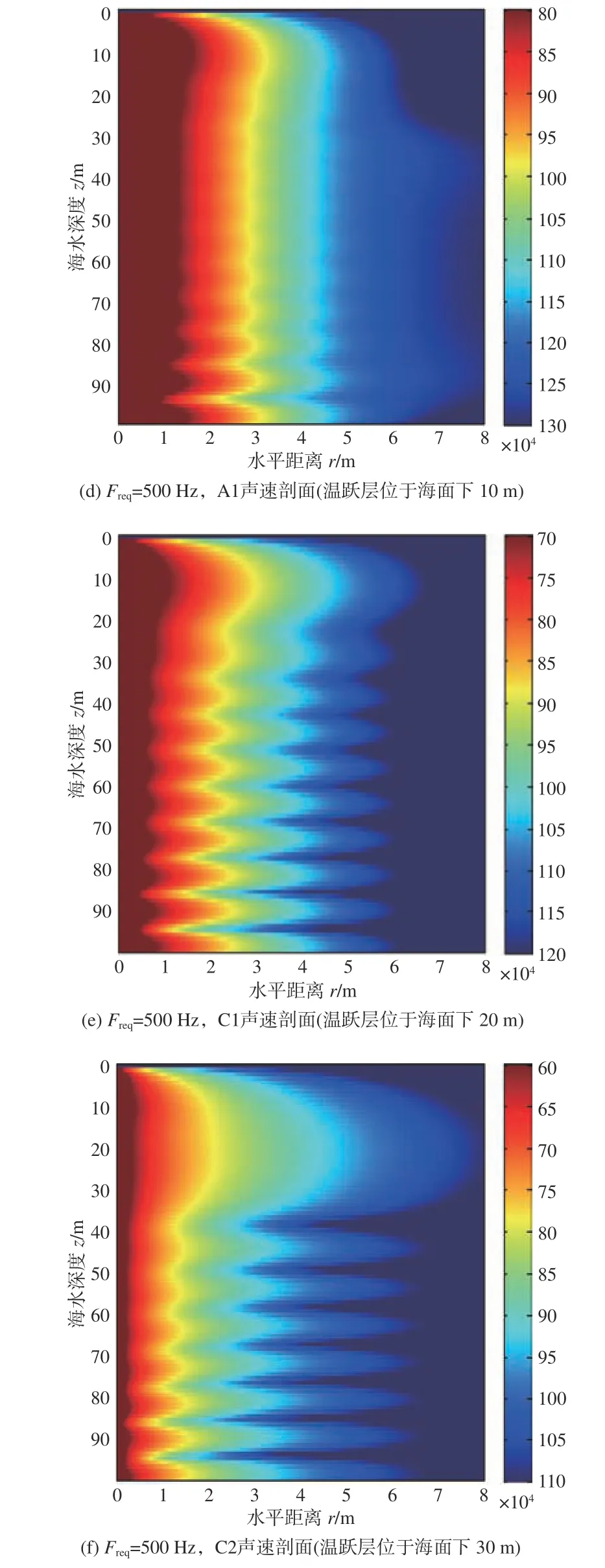
图6 声源深度zs =10 m 时不同频率下不同温跃层位置的声传播损失伪彩图Fig. 6 Transmission loss versus depth and range for fixed source at 10 m with different locations of thermocline for different frequencies

图7 给出了声源深度zs=50 m 的传播损失伪彩图。由图中可以看出：当声源深度zs=50 m 时，声场的传播损失明显小于声源深度zs=10 m 时的损失，最佳深度始终位于较深海水的等温层内，出现了类似于等梯度情况下的最佳频率的对称现象，即最佳深度在等温层内是对称的，且等温层厚度越小，对称现象越明显；此外，最佳深度现象也随着频率的增大更加明显。

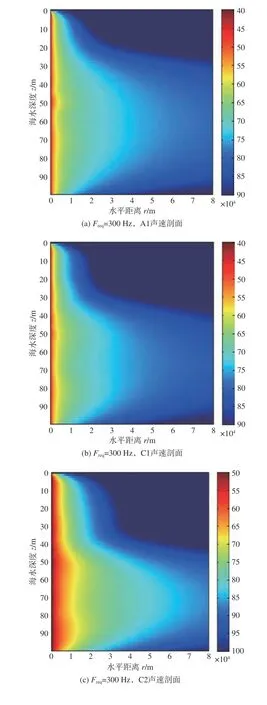
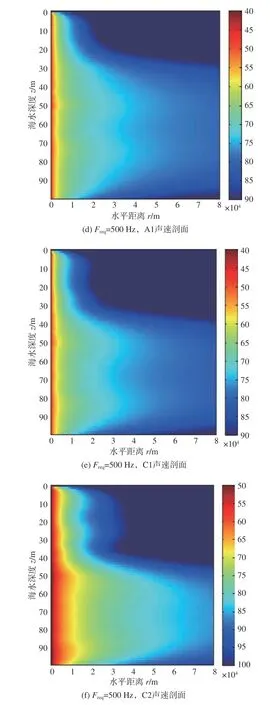
图7 声源深度zs =50 m 时不同频率下不同温跃层位置的声传播损失伪彩图Fig. 7 Transmission loss versus depth and range for fixed source at 50 m with different locations of thermocline for different frequencies

出现上述图7 所示现象的原因是：当声源位于温跃层或等温层时，海水中上层高声速混合层的存在使得声线在传播过程中的弯曲现象比负梯度声速剖面下的更为剧烈，因而声能量也就更容易集中在等温层内，声速较小的等温层会形成等声速的水平波导，声波在此波导中传播时就会出现类似于等梯度海水中最佳深度的对称现象，且最佳深度也是随着简正波个数的减少向等声速层的中间移动，最终落在等声速层中间处。

图8 给出了声源深度zs=90 m 的传播损失伪彩图。此时，声源位于等温层内，声传播损失与声源位于50 m 时类似，且都在等温层对称地出现了最佳深度。通过对比图7 和图8，发现声源越靠近海底，最佳深度的对称现象就越明显。这是因为从近海底处发出的声线在传播过程中其弯曲程度比海水层中部声源发出声线的弯曲程度更为剧烈，导致更多的声能量被困在等温层波导中，从而使得最佳深度现象更为明显。

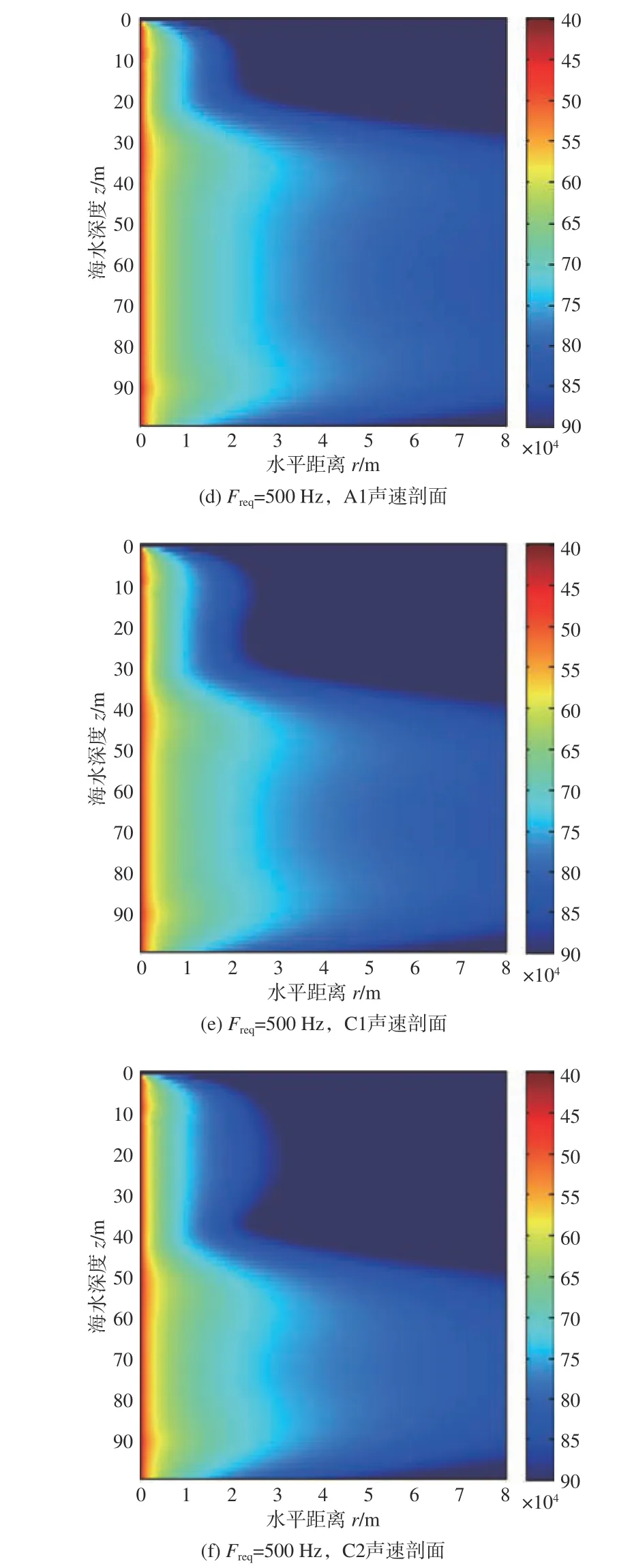
图8 声源深度zs =90 m 时不同频率下不同温跃层位置的声传播损失伪彩图Fig. 8 Transmission loss versus depth and range for fixed source at 90 m with different locations of thermocline for different frequencies

总结上述图8 中现象得出：在高频情况下，当声源位于混合层时，声场的传播损失较大，最佳深度位于声源深度，且混合层厚度越大，最佳深度现象越明显；当声源位于温跃层或等温层时，最佳深度出现了类似于等梯度情况下的对称现象，即最佳深度在等温层内是对称的，且等温层厚度越小，对称现象就越明显；随着传播距离的增大，最佳深度逐渐向等温层中间移动。