最小示数为多少——浅析第32届北京市高中力学竞赛预赛的一道圆周运动题

◇ 曾德才

本文以2019年第32届北京市高中力学竞赛预赛第11题为例，分析物体在竖直平面内做圆周运动时一般位置处竖直方向的分力情况，并进一步求出极值，得到压力传感器的最小值．以期增强学生对物体在竖直平面内做变速圆周运动问题的理解，提升学生用数学方法解决物理问题的能力．

图1

原题如图1所示，质量为50kg的同学站在压力传感器上，他手握绳子的一端．绳子的另一端系一个质量为1kg的小球，绳长为0．5m．使小球绕手握绳端的端点在竖直平面内做圆周运动，且小球恰能通过圆周的最高点，g取10m·s－2，则下列说法正确的是( )．

A．物体在最高点的速度为零

B．物体在最低点的速度大小为5m·s－1C．传感器的最大示数为560N D．传感器的最小示数为500N答案:B、C．

这道题难度很大，错误率比较高，绝大多数学生选了B、C、D．笔者对参加考试的学生进行了问卷调查，统计表明，多数学生能够结合机械能守恒定律和圆周运动相关知识分析求解，解析步骤一般如下:

小球在竖直平面内做圆周运动，“恰能”通过圆周的最高点，即在最高点绳子的拉力FT＝0．

以小球为研究对象，假设小球在最高点的速度为v0、绳长为r，根据牛顿第二定律有，解得代入数据得

设小球在最低点的速度为vmax，从最高点到最低点的过程中，根据机械能守恒定律得解得代入数据解得

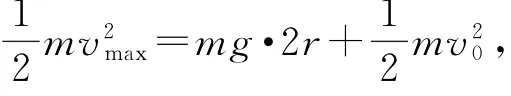
以人为研究对象，人同时受到三个力的作用:重力Mg，压力传感器的支持力FN，绳的拉力为FT．

小球在最高点时，绳子的拉力FT＝0，对人有FN1＝Mg，代入数据得FN1＝500N．故小球在最高点时，压力传感器的示数为500N．

小球在最低点时，对人有

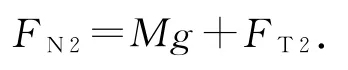
对小球有

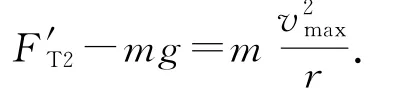
根据以上分析，学生认为:在最低点处，小球的速度最大，绳子拉力最大，压力传感器的示数最大；在最高点处，小球的速度最小，绳子的拉力最小，压力传感器的示数最小，故认为答案是B、C、D．

问题出在选项D，在最高点处，压力传感器的示数最小吗?

教材中关于变速圆周运动的阐述是从受力特点出发，根据力F产生的效果，将F分解为跟圆周相切的分力F1和指向圆心的分力F2，之后并没有进一步拓展和深化．对于物体在竖直平面内的变速圆周运动，教学中通常以汽车过拱形桥、凹形桥为例，分析汽车在圆周最高点或最低点的受力特点并展开讨论，学生所做的习题大多数考查“绳模型”“杆模型”中物体在最高点或最低点的速度、受力问题，这导致学生形成思维定式，错误地认为在最高点处，小球的速度最小，绳子的拉力最小，压力传感器的示数最小，并没有严谨地分析压力传感器的示数变化，不假思索地错选D选项．

图2

压力传感器的示数除了与人的重力有关，还与绳对人的拉力有关，而绳上的拉力大小又与小球运动的位置有关．因此应分析当小球在竖直平面内做圆周运动时，在哪个位置上绳对小球的拉力的竖直向下的分力最大，那么在该位置时绳对人的竖直向上的拉力也最大，则压力传感器对人的支持力就最小，压力传感器的示数最小．

设小球质量为m，在最高点速度为v0，当小球运动到上半圆的任意一点C时，如图2所示，绳与竖直方向的夹角为α(0≤α＜90°)，设此时小球的速度为v，绳子对小球的拉力为FT，拉力的竖直分力为FTy，沿半径方向，根据牛顿第二定律有

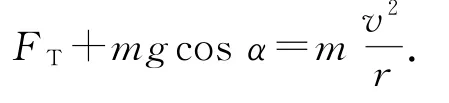
拉力的竖直分力为

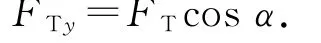
小球从C点到最高点的过程中，根据机械能守恒定律得

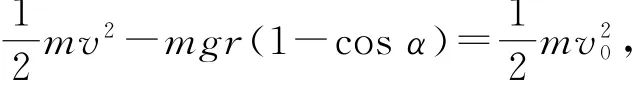
解得

由上式可知，拉力的竖直分量大小不仅与小球的质量、小球在最高点的速度、圆周运动半径有关，还与绳与竖直方向的夹角α有关，且FTy与cosα为二次函数关系

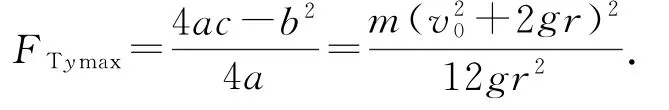
小球在C处时，对人FNC＝Mg－FTy．

FTy有极大值时，FNC有极小值，即当绳与竖直方向的夹角为α＝60°时，压力传感器的示数最小为FNmin．故

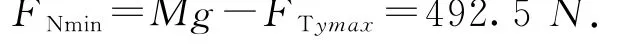
由以上分析可知小球在最高点处，压力传感器的示数并不是最小值，最小值的大小由小球的质量、最高点初始速度、圆周运动半径、绳与竖直方向的夹角等因素共同决定．

在教学中，教师要积极引导学生思考、讨论，及时发现自己存在的问题，分析物体在竖直平面内做圆周运动一般位置的受力情况，通过分析向心力来源问题，发展学生的科学论证能力，以拓展学生的知识面，培养学生主动探索科学问题的意识和能力，帮助学生加深对竖直平面内圆周运动、牛顿运动定律、机械能守恒定律、力与速度分解等物理规律的理解，提升学生分析问题、解决问题的能力，凸显物理科学思维的培养，促进学生物理学科核心素养的形成．