基于ANN模糊协同方法半导体产业成本预测研究

姚晓童， 李 林

(上海理工大学 管理学院， 上海 200093)

半导体产业是资金技术密集型产业，为使企业盈利，生产财务规划尤为重要，而工厂的生产和财务规划是基于成本估计[1]，同时，市场竞争激烈，通常由于供过于求而使平均销售价格低于单位成本，使企业无利可图[2]。因此，半导体单位成本预测是极具现实意义的课题。

国内外学者开展了大量关于半导体成本的研究。Carnes基于晶圆生产的4阶段，即制造、分类、包装、测试，建立了晶片单位成本的计算公式[3]; 俞静等基于晶圆生产工序，以工程经济学的角度对晶圆制造成本进行预测；Liu等人[4]进行工厂模拟，估计与生产计划相关的周期性产出和总成本，通过总成本除以产量间接预测了晶圆单位成本；Burkart和Kolar[5]建立了太阳能半导体的单位成本与芯片大小和封装成本的线性函数实现半导体单位成本预测。以上研究都从不同角度考虑晶圆成本，但没有考虑在实际生产中半导体成本的学习过程。对半导体成本趋势进行建模，可帮助企业分析产品利润，做好投资规划，面对外部风险时可及时采取有效措施应对风险。

针对半导体成本趋势预测，Chen等[2,6-7]提出了一种模糊协同智能方法来估计某晶圆厂某产品类型的有效单位成本。该方法直接对单位成本学习函数进行建模，降低了过程复杂度。但依然存在以下问题：①对于非凸QP问题很难求得最优解。②专家对模型参数的设置可能导致问题没有可行解。针对以上问题，本文构建了多代理人工神经网络(ANN)代替求解QP问题对模糊单位成本学习函数进行建模。

1 ANN模糊协同方法

1.1 半导体单位成本学习模型

半导体单位成本在生产阶段初期是一个学习过程，构造单位成本学习模型可以观察单位成本发展趋势，预测未来单位成本。由于获取信息的不确定性及影响因素的复杂性，为降低预测过程中的不确定性，将单位成本学习模型(1)与三角模糊数相结合，构造新的单位成本学习模型(3)。为简化计算，根据三角模糊数运算规则，模型(3)计算可近似为模型(4)。

(1)

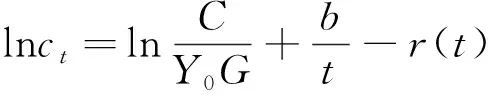
(2)

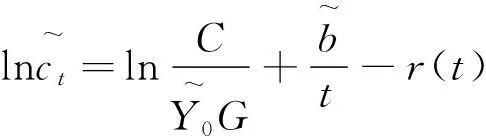
(3)

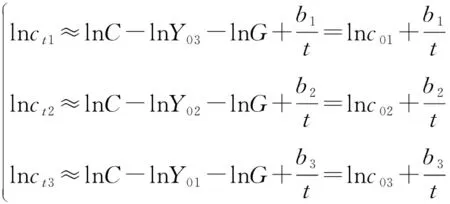
(4)

目前有多种方法求解式(4),例如文献[8]通过最小化单位成本预测范围构建了线性方程LP；文献[9]提出最大化满意度水平构建了二次规划方程QP1；文献[10]通过综合LP与QP1的要求，提出了带有权重的最小化单位成本预测范围的二次规划方程QP2，但求解QP问题的全局最优解仍然是一个难题，且权重的确定没有确定的规则；文献[6]改进了可用的模型构建了两个非线性方程NLP1、NLP2拟合半导体单位成本学习模型，求解NLP问题仍是一个挑战；文献[11]将NLP1与NLP2改为等效的QP问题，以简化求解过程。当前可用的模糊协同方法来预测半导体的单位成本学习过程都是基于求解数学规划问题。

ANN在面对难以判断的输入输出关系时仍然表现出很好的拟合特性，因此成为时间序列非线性建模最常使用的模型[12]。基于此构建了一个两层神经网络来拟合单位成本的学习过程。本文所用的参数及变量汇总在表1。

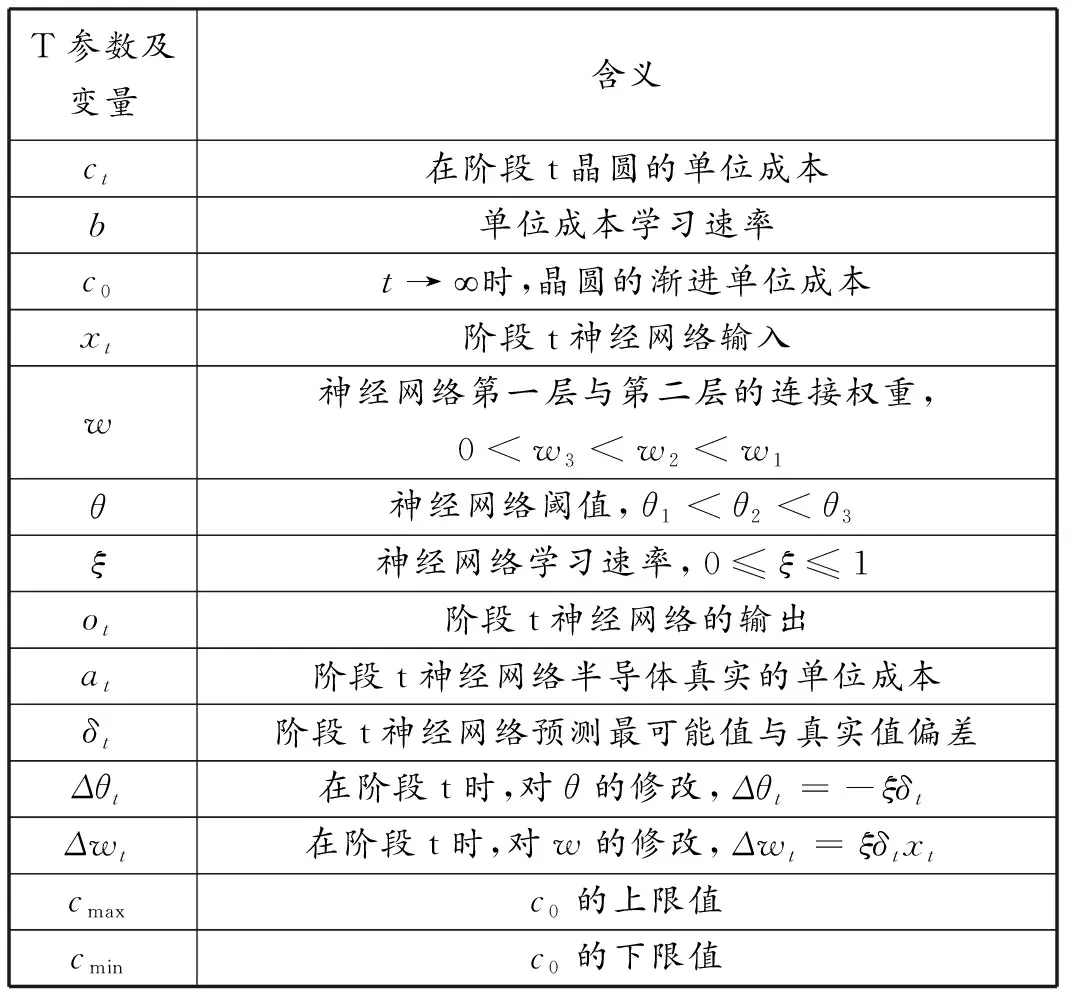
表1 参数及变量汇总

1.1.1 ANN模型构建

ANN来拟合单位成本学习过程。模型构造如下。

4)输出节点的输出值为节点输入wxt与阈值θ进行比较即wxt(-)θ；

1.1.2 ANN训练算法

本文所构建ANN模型有如下性质。

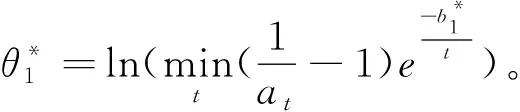
根据以上性质与定理，对现有的梯度下降算法进行改进，以适应带有参数限制(w<0)的ANN训练。训练算法如下：

1)估计单位成本渐进值cmin，cmax。

2)确定模型参数w，θ，ξ。

烟叶的糖、氮、碱、钾等常规化学成分的含量及比例，是烟叶内在质量的基础，并在一定程度上决定了其感官质量[17]。烟叶生长发育的差异，同样会影响到叶片内含物的积累量，从而影响烟叶化学成分的含量[19]。研究结果表明，3个处理(移栽期)处理中，上部叶和中部叶的总糖、还原糖、总氮、烟碱、钾及氯的含量均有所不同，与陈义强等[18-19]的研究结果相一致。总体来看，3个处理上部叶和中部叶的总氮、烟碱的含量较为适宜，不足之处是糖含量偏高、钾与氯的含量偏低，导致糖碱比偏高而氮碱比偏低。因此，在烟叶生产中，需要进一步改进栽培措施，以促使其烟叶的化学成分更加协调。

5)计算预测值与真实值偏差δt。

6)计算模型参数偏置Δwt，Δθt。

7)判断所有样本是否都参与训练，如果是则转第8步，如果否，则返回第3步。

8)计算均方差mse。

9)更新权重与阈值w2，θ2。

10)判断w2<0，mse<10-6 ，如果是，则转第11步，如果否，则转第3步。

11)更新模型参数w1，w3，θ1，θ3。

1.2 模糊聚合

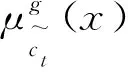
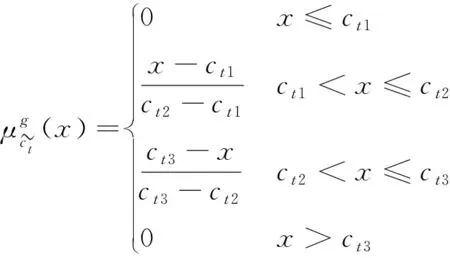
(5)

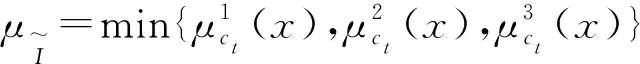
(6)

1.3 BPN反模糊化

BPN广泛应用于复杂模型的线性拟合中，并表现出良好的拟合特性。为获得清晰的预测值，构建三层BP神经网络去模糊化，得到单位成本预测清晰值，步骤如下：

1)多边形的每个交点作为BPN输入，如果多边形有5个交点，则BPN输入点有10个。由于每个时间周期多边形交点数不同，BPN输入点数由各个周期多变形最多的点数决定。点数不足，输入值为0。

2)根据经验将BPN隐藏层点数设置为输入点数的2倍。

3)采用Levenberg-Marquardt训练算法[13]。

2 DRAM产品实例应用

为验证所提出模型的有效性与精确性,本文选用10组包含1G DRAM产品成本数据进行仿真[16],数据如表2。按照7：3原则，将前7个周期数据用来训练ANN，后3个周期数据用来评价模型。由3名代理独自执行ANN模糊预测，独立设置初始参数，经过反复调整，ANN模型初始参数如表3。

本文用MATLAB2014b对所提出的FCI方法进行验证，ANN预测半导体单位成本与模糊聚合通过编写代码实现，用神经网络工具箱完成BPN解模糊化。

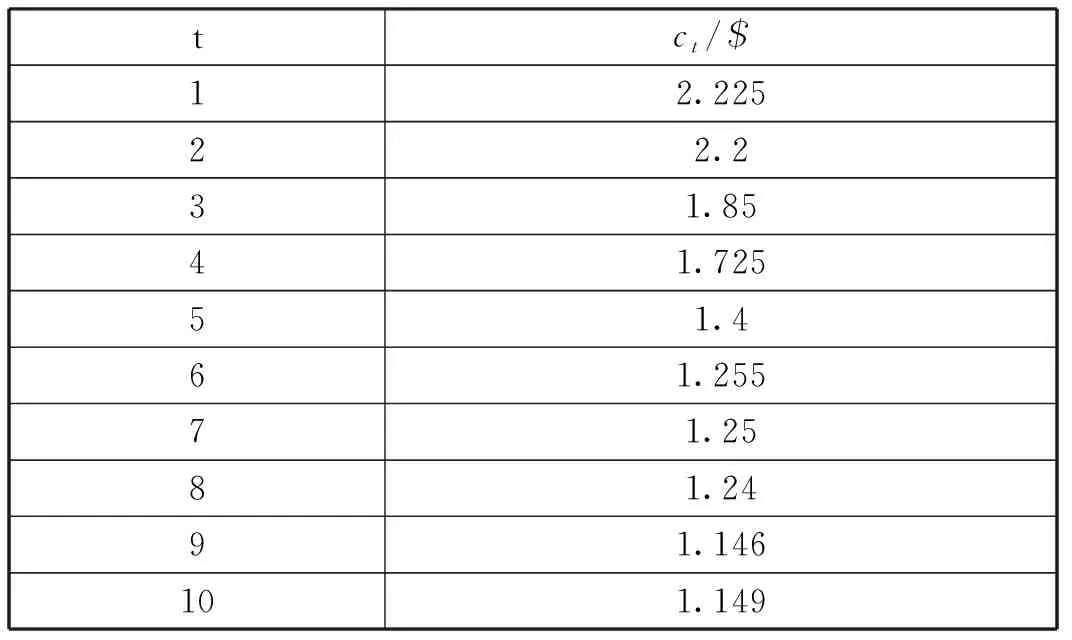
表2 真实单位成本

表3 初始参数设置

根据求解模糊线性回归方程(4)，得到模糊单位成本预测学习模型如图1-图3，从图中可以看出在训练数据集上3位代理所使用的FCI方法均包含实际的单位成本值。缩小预测范围，使预测结果逼近真实值，我们采用模糊聚合函数(6)将3位代理的预测结果进行聚合。聚合后的结果如表4。

为得到单位成本精确值，我们将表4的坐标点作为BPN的输入，由于BPN对初值的敏感性[17]，我们用随机初始值重复实验20次，取最佳表现预测值。由于数据集较少，选用10折交叉验证的方法，即选取1周期作为测试集，其他作为训练集，由此循环10次。采用平均范围、MAE、MAPE、RMSE等评价指标进行性能分析，并与Chen提出的NLP-BPN方法、Chen 和 Chiu提出的NLP/QP-BPN与本文提出的ANN-BPN做比较，结果汇总在表5。

表4 模糊聚合点坐标

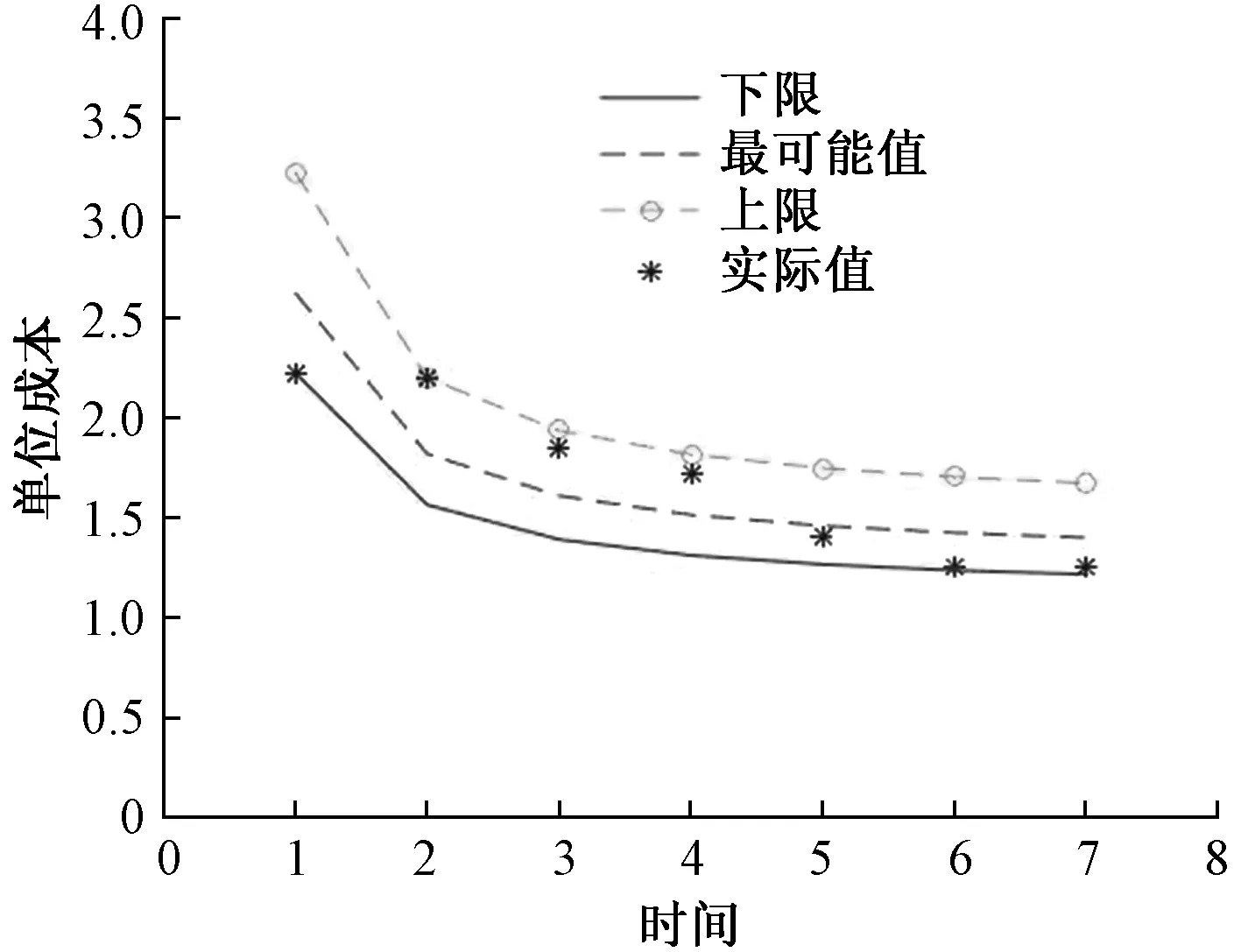
图1 代理1对单位成本的模糊预测

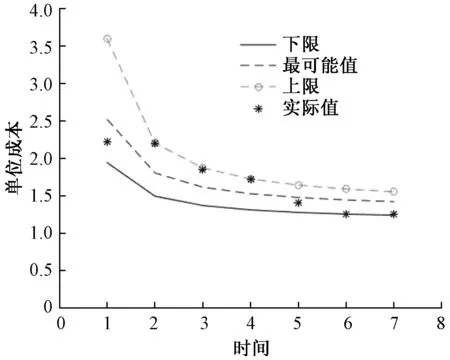
图2 代理2对单位成本的模糊预测

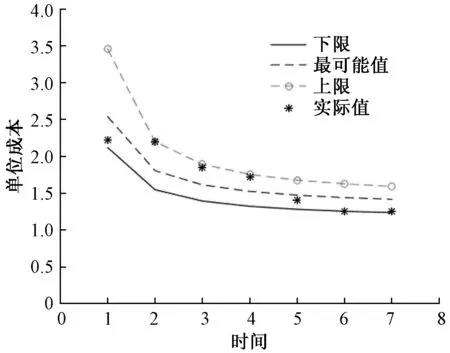
图3 代理3对单位成本的模糊预测

由表5可知，本文提出的ANN模糊协同方法相较于传统的模糊协同算法在MAE、MAPE、RMSE三项指标上有显著提高，有利于提高半导体单位成本的预测准确性。平均范围指标也取得了较好的性能。

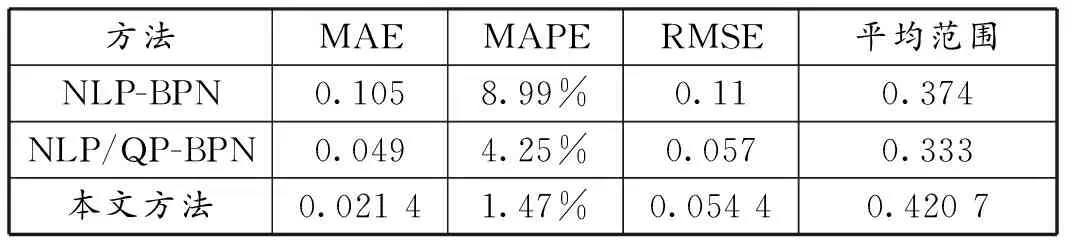
表5 不同方法预测表现

3 结语

考虑到单位成本学习现象，本文构建两层ANN拟合单位成本学习函数并于三角模糊数结合，ANN方法是单位成本预测一种新的尝试，避免了普遍数学编程方法参数设置问题以及二元方程最优解不易确定问题。针对半导体单位成本受多种不同因素影响而导致单位成本的预测复杂性与不确定性，本文使用3名代理单独设置ANN初始参数，得到单位成本预测三角模糊值，使用模糊聚合方法将三位代理的三角模糊值聚合缩小预测范围，提高预测准确性。聚合结果使用BPN解模糊化，得到单位成本预测精确值。实验结果证明，本方法预测半导体单位成本与现有方法比较，预测性能明显提高，为求解半导体学习模型参数提供了一种新的思路。