基于BB84 协议的低轨卫星下行量子密钥分发链路评估

耿 健，金 文，闫新峰，赵雅琴，房伟红

（北京航天长征飞行器研究所，北京，100076）

0 引 言

建立全球广域量子通信网是包括中国在内的世界各航天大国面向未来的一个重要需求。利用地轨卫星或飞行器平台实现天地间量子密钥分发（Quantum Key Distribution，QKD）已被广泛认为是当前最有可能建立广域量子通信网的方式。随着QKD 理论和实验方面取得越来越多的可喜成果，构建全球量子卫星组网或将成为可能[1,2]。

星地QKD 链路是基于量子卫星的广域QKD 系统的关键组成。按照信息传输方向分类，星地量子密钥分发链路的实现方式可分为：下行（卫星发-地面收）、上行（地面发-卫星收）和卫星反射（地面发-卫星反射-地面收）3 种主要方式。相比而言，下行方式更易获得较高的星地量子密钥分发速率[1]。主要的密钥分发协议有以BB84、B92 协议为代表的基于单光子非纠缠态协议、以Ekert91 和BBM92 为代表的单光子纠缠态协议、以GG02 为代表的连续变量密钥分发协议和基于测量设备无关类协议等[3]。其中，以基于诱骗态的BB84协议在当前工程应用中最为广泛和成熟。本文考虑基于诱骗态的BB84 协议的星地下行QKD 链路。

文献[4]～[6]集中于在单颗卫星场景下的星地QKD链路的光学相关参数评估和链路分发时间分析。本文在现有研究基础上，分析评估典型太阳同步轨道（Low Earth Orbit，LEO）高度及星座（Walker 星座）规模与平均密钥分发长度的关系。仿真考虑了望远镜自身反射镜对光路的遮挡、偏振极化误差和光路指向误差等非理想因素下的有限长度安全密钥的计算。所得结果对设计全球量子卫星组网系统具有一定参考意义。

1 原理

星地QKD 系统主要包括：经典通信模块、光路捕获跟踪模块和量子收发模块。其中，经典通信模块主要利用无线通信技术传输星地双方的初始位置、姿态信息以及在QKD 过程中交互辅助确定密钥的公开信息。光路捕获跟踪模块完成收发间光学望远镜指向的精确对准及跟踪保持。量子收发模块则主要完成基于特定协议的量子密钥产生与分发功能。

基于卫星的广域量子密钥分发过程一般包括3 个阶段：第1 阶段，当卫星经过地面站A 上空时与地面站A 进行QKD，从而使双方共享密钥 cA；第2 阶段，当卫星经过地面站B 上空时与地面站B 进行QKD，从而使双方共享密钥 cB；第3 阶段，当卫星再次过境地面站A 时，将Bc 作为信息，用密码Ac 对信息 cB或其部分内容进行加密并通过经典无线信道发送给地面站A。至此，地面站A 可解密得到地面站B 的密码 cB全部或部分内容。

由于大气信道对偏振光子的保偏度和偏振态的影响很低，BB84 协议在星地场景下适合以偏振光为载体。基本的BB84 协议使用两组非正交基进行编码，利用非正交量子态的不可克隆性质，使得窃听行为能被发现。当前工程应用上，在BB84 协议基础上增加了诱骗态以克服非理想光源带来的安全隐患。文献[7]指出采用三态的诱骗态能够逼近最优性能，其中三态指信号光、诱骗光和真空态光。基于诱骗态的BB84协议可简要概括如下[3]：

首先，发端（卫星）对信号光源和诱骗光源（及真空态）光脉冲按照BB84 协议进行编码，3 种光源的脉冲以一定的比例随机的发送给收端（地面站）。其次，地面站收到所有光脉冲后，卫星公布各脉冲所采用的光源。然后，地面站统计信号源、诱骗源的透过率（透过率为接收到的数量与发送的数量的比值）。如果前者比后者小很多，则认为本次分发过程受到分离光子数攻击，放弃本次通信；反之，按照BB84 协议保留收发双方使用相同基下的测量结果作为筛选码，通过进一步的纠错处理和密性放大得到最终安全密钥。

对于星地QKD 系统，安全密钥率（或安全码率）和地面站在一定时间内可获得的总安全密钥长度是系统的重要性能指标。在确定QKD 分发协议后，影响安全码率和总码长的主要因素包括：考虑多种实际因素下的光链路的损耗、暗计数与背景噪声计数、偏振误差、安全性和可靠性指标以及卫星的轨道与星座规模等。本文建立信道传输和安全码率计算的仿真模型并据此对比分析不同卫星（星座）场景下的安全密钥长度性能差异。

2 仿真模型

2.1 响应率和误码率

系统仿真模型中的关键参数说明如表1 所示。

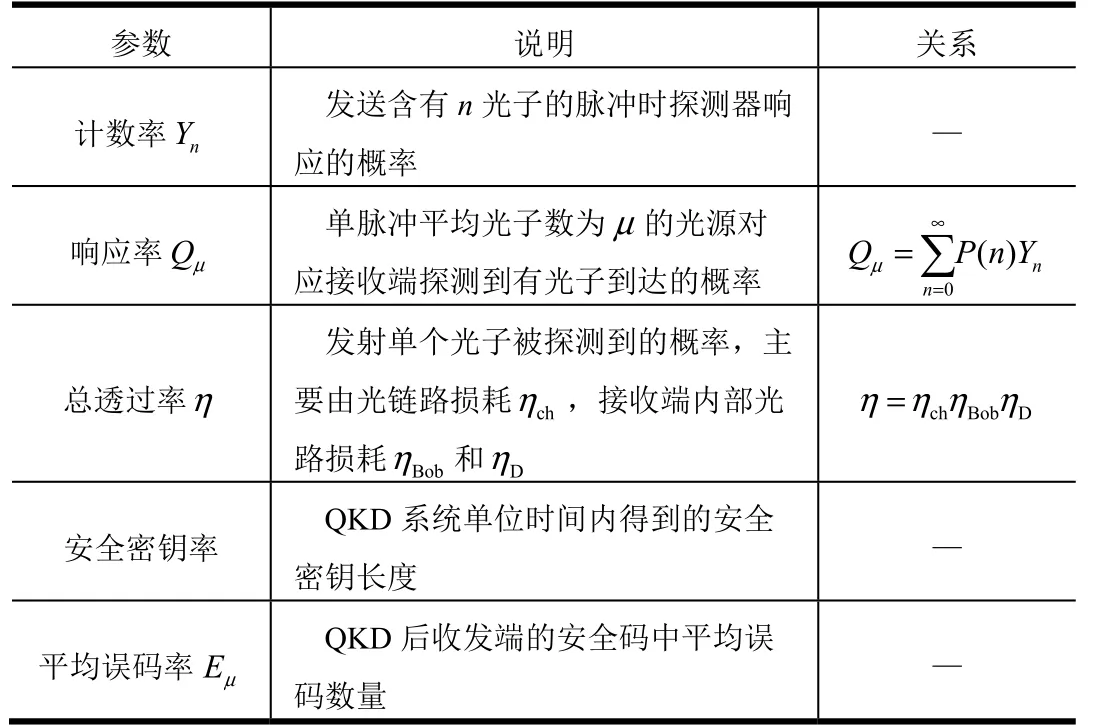
表1 主要参数说明Tab.1 Main Parameters Discription

影响系统安全密钥率的2 个主要因素是响应率和误码率。定义 Yn为发送端发送含有n 光子的脉冲时，接收端探测器响应的概率；Qn= P( n )Yn发送端发送脉冲为n 光子脉冲且接收端探测器响应的概率，其中 P ( n )为发送脉冲中含有n 个光子的概率，为泊松分布。当发送端发送脉冲光子数为0 时，对应的概率 Y0由探测器暗计数和背景噪声产生。

对于单个光子，QKD 系统的总透过率为η = ηchηBobηD，其中ηch为光链路损耗，ηBob为接收端内部光路损耗，ηD为探测器效率。对于平均光子数为μ 的弱相干光源，可求得总响应率为[3]

在无窃听情况下，天地量子QKD 系统的量子比特误码率来源主要有2 部分。第1 部分是来自系统光路的非理想性。在本文场景中主要表现为偏振对比度引起的误码率。令该误码率为 edet，其表示了筛选码中即使没有暗计数和Eve 攻击而存在的误码概率；第2 部分主要来自探测器的暗计数和背景噪声[7]。上述两部分误码来源可认为相互独立。

对于误码来源的第1 部分，发端和收端组成的系统的等效偏振对比度ER 引起的误码率可表示为[9]

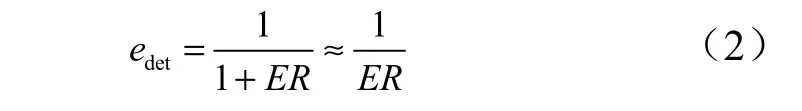
通过实时偏振补偿措施，通常可以将系统偏振对比度ER 控制在100 以上，对应的误码率小于1%。

对于误码来源的第2 部分，假设所有探测器的指标相同，令单台探测器的暗计数率为 pd（计数/脉冲），探测效率为ηD，背景噪声产生的计数率为 pBG（计数/脉冲）。进入探测器的背景噪声计数率为 pBGηD，在BB84 协议中平均仅有一半的计数会体现在安全密钥中。因此有：

令Eμ为安全密钥的平均误码率。当发送端使用平均强度为μ 的弱相干光源时，平均误码率为[3]

式中0e 由暗计数和背景噪声引起误码率， e0=1/2。

2.2 安全密钥长度

考虑基于诱骗态的有限筛选码长度下安全密钥长度计算。假设信号光、诱骗光和真空态光三者的发射概率分别为 Psignal， Pdecoy， Pvacuum。令信号源的光源平均光子数为μ，诱骗态光源的平均光子数为ν 。对于真空态光源，其响应率和量子比特误码率（Quantum Bit Error Rate，QBER）分别为 Qva= Y0和 Eva= e0。通过该值可以准确的监测到暗计数和背景噪声的信息。对于诱骗态，其响应率和量子比特误码率分别为Qν和Eν，其计算同2.1 节。

诱骗态方式下的有限长度安全密钥码长下界为[10]

式中 q 为BB84 协议效率， q=1/2； Nμ( Nv)为接收到的信号态（诱骗态）计数值， Nμ= QμPsignalfpulseT；Nν=QνPdecoyfpulseT ，其中 fpulse为脉冲频率，T 为观测时间；H2( )为二进制熵函数； f ( Eμ)为纠错效率；Δ= 2lo g2(1/ ( 2 ( ∈ −− ∈EC)))+，其中∈为最终密钥不安全的概率， ∈EC为最终密钥错误的概率。一般可取 ∈= 10−9~10−5，∈EC= 10−10~10−9。为可调参数，具体取值为通过数值计算满足约束∈ − ∈EC>≥0使得安全码下界最大的结果。

当ν <μ 时， Q1下界和 e1的上界可分别表示为[3]

当μ <ν 时，将式（6）中 Q1的下界和 e1的上界中ν和μ 互换可得到相应的下界：

将 Q1下界和 e1上界代入式（5）可得安全码长。

2.3 光链路损耗

星地光路损耗 ηch主要由光的衍射和指向偏差造成。收发端相对位置关系如图1 所示。图1 中坐标系原点为发送端望远镜平面中心，发射端镜面位于OXY平面，Z 轴正方向为弱相干光的传播方向。发送端望远镜平面上的点可由 vt=( xt, yt,0)表示，收发端望远镜间距由 zr表示，指向偏差角为 σp。

图1 收发光路传播示意Fig.1 Diagram of the Optical Path

设偏振光波长为λ。基于瑞利-索墨菲衍射理论，理想情况下接收端镜面点 vr=( xr, yr,zr)处的光强Iideal( vr)可表示为[4,11]

式中 I0为发送端最大光强； St为发送端望远镜平面中除去反射镜面积后的有效区域。由发送端光斑的圆对称性易得收端平面上的光斑也为圆对称，因此只需利用式（9）计算出收端光斑中任意一条径向上的光强分布，即可表征收端光斑。仿真中，取x 轴向的光强分布，即令 yr=0 。

指向偏差角建模为零均值标准差为 σp的高斯随机变量。偏离的方向为[0,2π)均匀分布。于是，当存在指向偏差时，接收光斑的中心点偏离理想情况下光斑的中心点距离 rp为零均值标准差为 zrσp的高斯随机变量，rp的概率密度函数为

式中 Sr为接收端望远镜平面中除去反射镜面积后的有效区域。

2.4 卫星轨道与星座

本文考虑两类场景：单颗太阳同步轨道卫星和基于Walker-δ 星座的LEO 卫星系统。对于太阳同步轨道卫星，同一地面站每天能够在大致相同的地方时段内观测到卫星过境，从而实现定期的天地QKD。Walker星座具有几何构型意义上的对称性（均匀性）的优点，在低轨卫星通信和导航领域得到广泛应用。常用卫星数目/轨道平面数/相位因子（N/P/F）作为Walker 星座的构型码。其中，变量相位因子F 用来确定相邻轨道面相邻卫星间的相位差 Δωf， Δωf=2π F /N。

3 评估结果

利用上述模型，从平均密钥长度和链路持续时间两个方面，比较不同轨道卫星场景下卫星-地面及卫星-卫星QKD 链路性能。如无特殊说明，仿真参数设置如表2 所示。本文假设卫星过境时，光链路的天顶角在±70°以内时可实现精确跟瞄并进行密钥分发。使用卫星工具包（Systems Tool Kit，STK）计算星地、星间链路距离和持续时间。在STK 的场景中地面站位于赤道上，仅认为地面站当地时间20 点至次日凌晨4点期间的卫星过境为有效过境。太阳同步卫星轨道的降交点经度同地面站经度。

表2 主要仿真参数设置Tab.2 Main Simulation Parameters

图2 给出了卫星-地面站和卫星间QKD 光路损耗与距离的关系，图中距离增加一倍，光路损耗增加约6 dB。在诱骗态方案中，信号光和诱骗光的平均光子数 μ ,ν 的最优取值与系统链路损耗大小相关。仿真中，对于每种卫星轨道或星座配置，选择当前配置下可得到的最大平均安全密钥长度进行比较。根据仿真结果，对于本文考虑的LEO 卫星，不同轨道和星座下平均光子数 μ ,ν 的最优组合( μ ,ν )取值略有不同，但最优值在(0.25，0.55)附近或(0.55，0.25)附近。

图2 光链路损耗与距离的关系Fig.2 Optical Pathloss VS Distance

单次过境总密钥长度由密钥率和持续时间共同决定。链路卫星轨道越低，其QKD 光路损耗越小，而QKD 持续时间却越短。图4 给出了太阳同步卫星单次过境所得到的最大平均安全密钥长度及对应的QKD持续时间与卫星轨道高度的关系。从图中可以看出，当轨道高度从200 km 增加至1300 km 时，轨道高度变化了6.5 倍，链路的持续时间增加了约13 倍，而平均安全密钥长度仅下降了约50%。相比持续时间的变化，平均单次过境的安全密钥长度随轨道高度的增加以较缓慢的趋势下降。

图3 单卫星单次过境密钥长度和链路持续时间Fig.3 Average Secure Key Length under a Single Satellite Pass VS Link Duration

卫星星座可以弥补单个LEO 卫星过境时间短的问题。相比于较高轨道的卫星场景，地面站可以通过与更多的较低轨道卫星进行密钥分发来获得更大的密钥总量。图4 比较了不同轨道高度和卫星数量的Walker星座下地面站平均每天获得的密钥总量以及密钥分发时间占总时间的比例，其中总时间指每晚20 点至次日凌晨4 点的时间长度。考虑了5 个Walker 星座，分别为200 km 轨道高度下（24/12/1）Walker 星座、（10/6/1）Walker 星座，400 km 轨道高度下（12/9/1）Walker 星座、（10/6/1）Walker 星座和800 km 轨道高度下（10/6/1）Walker 星座。从图4 中可以看出，轨道越低的星座在获得安全密钥的长度上优势越大。对比图4 和图3 还可以看出通过增加卫星数量，可大幅提升每天地面站得到的安全密钥总长度。

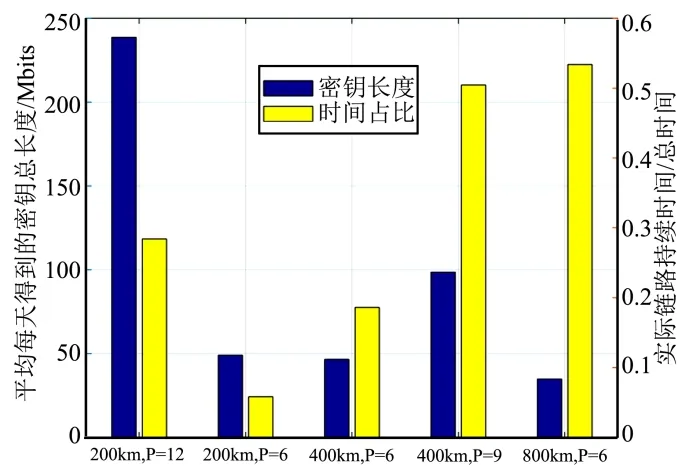
图4 不同星座下平均每天密钥长度及实际链路建立时间占比Fig.4 Average Secure Key Length Per Day and the Link Available Time to the Total Time Radio under Different Configurations

最后，利用链路模型评估星间密钥分发的平均密钥长度和持续时间。星间密钥分发可用于密钥的转发和交换，基本原理与星地洲际密钥分发原理相似。受到星载卫星望远镜能力的限制，星间QKD 链路损耗通常比星地链路损耗大，这限制了星间QKD 的距离。以200 km 轨道高度下（24/12/1）Walker 星座和400 km轨道高度下（12/9/1）Walker 星座为仿真场景。图5和表3 比较了2 种星座场景下相邻两个轨道平面上最近的两颗卫星的距离分布情况、平均每天可交互的密钥量和链路持续时间。两颗卫星的星间距离变化范围较大，在地球南北极上空时星间距可达最小，在赤道上空时星间距最大。从仿真结果看，两颗卫星适合在轨道交汇的区域附近进行星间量子密钥分发，而在其它时段星间密钥分发能力十分有限。这种使用方式与经典基于无线通信的卫星组网信息交换的实现方式有所区别。

图5 相邻平面相邻卫星星间距离分布Fig.5 The Distance Distribution of Two Adjacent Satelletes on the Two Adjacent Planes

表3 星间密钥分发性能Tab.3 Performance of Inter-satellete QKD

从仿真结果还可看出，地面站每天进行QKD 的时间（即每天密钥分发持续时间）是表征一个实际QKD系统的密钥分发性能的重要参数。仿真结果表明，单个卫星的星地QKD 链路持续时间与卫星轨道高度成反比例。然而，提高链路持续时间更有效的方式是增加卫星星座的规模。若仅从安全密钥量的角度出发，轨道越低的星座越能实现更好的性能。这主要有两方面原因：一方面，在地面站同一时间只能与一颗卫星进行QKD 的假设下，仿真结果显示增加轨道较低的卫星星座规模能够显著提升地面站的安全密钥长度；另一方面，轨道高度越低的卫星将有更多的机会服务于其它地面站，从而实现多个地面站间的量子密钥分发。

此外，为了提高整个系统的密钥分发能力，可将地面站放置于多颗卫星轨道交汇点的下方。一方面，地面站能够与多颗卫星同时交换量子密钥，另一方面不同轨道的多颗卫星间也可以相互进行量子密钥分发。例如，若在南极点布置地面站，对于400 km 轨道高度下（12/9/1）的Walker 星座，在不区分白天黑夜的情况下该地面站平均每天可与不同的卫星分发获得共5263 Mbit 的量子密钥。因此，在多个轨道平面交汇处下方的地面站适合承担密钥交换的工作。

4 结 论

基于仿真模型，本文对星地下行QKD 链路与卫星轨道高度及星座规模的关系进行评估和分析。仿真结果表明LEO 卫星平均单次过境与地面站分发的安全密钥长度随轨道高度的增加以较缓慢的趋势下降。尽管如此，通过降低卫星轨道高度、增加卫星数量，可以显著提升地面站可获取的密钥总量。因此，较低轨道的星座更适合实现高速的量子卫星QKD 系统。此外，将地面站部署于多颗卫星交汇点的下方，对提升星地间的密钥交换能力有显著的作用。