注气式POGO 抑制系统模型研究

王 楠，容 易，胡久辉，张青松，秦旭东

（北京宇航系统工程研究所，北京，100076）

0 引 言

POGO 是液体运载火箭结构与其动力系统相互耦合而产生的纵向自激低频振动[1,2]，会使运载火箭的振动环境恶化，可能造成箭上敏感元件及仪器设备受损或结构超限，对于载人航天，还会使宇航员出现身体不适，甚至危害宇航员的生命安全。因此，POGO 抑制是影响火箭飞行可靠性甚至飞行成败的一项重大关键技术。

为抑制POGO 振动，通常在推进剂输送管路系统上安装蓄压器，改变动力系统固有频率特性，以此削弱和消除箭体结构与动力系统之间的耦合。中国现役长征系列液体运载火箭均使用了贮气式POGO 抑制技术，抑制装置为贮气式蓄压器[3～8]，而国外运载火箭则广泛使用了注气式POGO 抑制技术，核心装置为注气式蓄压器[9～13]。随着中国运载火箭技术的发展，POGO抑制系统装置从贮气式向注气式的跨代升级已是大势所趋。相比于贮气式蓄压器，注气式蓄压器具有如下特点：

a）能量值PV[6]可随蓄压器入口压力实时连续调节，对动力系统的调频能力更强；

b）蓄压器气枕为开式系统，工作过程中不断有气体的注入和排出，同时气枕与液体推进剂之间还存在质量交换；

c）蓄压器内气液界面的稳定性受注气和排气的控制，排气阻力过大时，气体可能涌入输送管内。

上述特点导致了注气式蓄压器动特性模型有别于金属膜盒式蓄压器，文献[14]开展航天飞机POGO 抑制设计时，未考虑注气和排气可能带来的影响。Ares I火箭POGO 抑制设计继承了航天飞机、德尔塔运载火箭的经验，蓄压器选型过程中详细讨论了充气过程中液位的变化规律[15]；万屹仑等[16]也对注气式蓄压器工作特性及动特性模型进行了讨论，认为气枕成分单一，没有深入讨论影响蓄压器动特性的因素。

本文建立了注气式POGO 抑制系统线性化动特性模型，分析对比注气式蓄压器与贮气式蓄压器性能的差异，并通过试验对动特性模型的正确性进行了验证。

图1 航天飞机注气式POGO 抑制系统Fig.1 Gas-injected POGO Suppression System of Space Shuttle

1 线性化控制模型

注气式POGO 抑制系统的核心是注气式蓄压器，蓄压器气枕为输送系统提供一个集中柔性环节，是决定注气式蓄压器POGO 抑制能力的关键，由于注气式蓄压器的气枕属于开式系统，在建模方法上与贮气式蓄压器有较大的不同。

图2 为一种注气式蓄压器的结构原理图，蓄压器设置有注气管路和排气管路，排气管路限制了液位高度，当液位较低时，气体从排气管排出，当液位升高时，液体也可以从管路排出。蓄压器气枕和液位在注气和排气的共同作用下维持稳定。

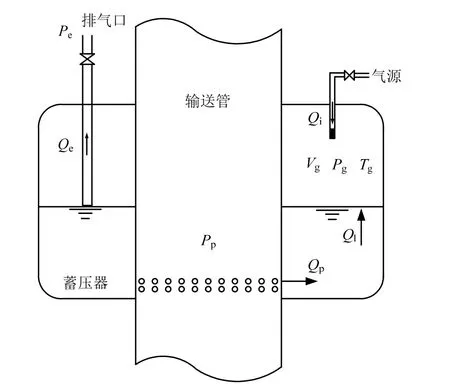
图2 注气式蓄压器示意Fig.2 Diagrammatic Sketch of Gas-injected Accumulator

为简化起见，不考虑气枕与推进剂之间的质量交换（即不考虑推进剂蒸发量和气体冷凝）。在脉动压力作用下，气枕的变化近似为等熵绝热过程；排气管始终保持和气枕接触，排气管无液体排出，气液界面做平移无大幅波动。对于气枕内气体有：

式中 Mg为气枕内气体总质量。

微分后有：

相比于气体，液体的可压缩性可以忽略不计，因此连通孔处的流量pQ 与气液交界面处流量lQ 相等，即：

式中lρ 为液体密度。

为了便于描述，规定以输送管内液体流向蓄压器的方向为正，即以使得蓄压器内气枕体积减小的方向为正。

式中 δ 为脉动物理量。

按照不可压流动方程有蓄压器入口压力pP 与气枕压力gP 的关系为[17]

式中aL 为蓄压器惯性；为蓄压器阻尼系数。

注气流量iQ 通常由供气管路上孔板控制，设计状态下孔板处于超临界流动状态，一般认为孔板流量不受下游扰动影响，因此 iQδ ≈0。

排气流量eQ 由下式决定：

式中 μ 为孔板流量系数；A 为孔截面积；k 为气体比热比；R 为气体常数。

对其进行小偏差线性化处理后可得如下形式的动态数学模型：

晌午，我到知青大院去还郝浮萍的自行车，她说，那个秃头刚走，他是来道歉的，还留下二十块钱，说是营养费。我说，既然伤得不重，就饶了他吧。郝浮萍面带难色，说，田青青已经去了公社，这事恐怕盖不住了。我知道秃头来道歉并赔钱，这肯定是赵世奎的点子。一旦这事捅到上边，必将引起一场轩然大波。

当处于超临界流动时，ε=0。

对于本文研究的注气式蓄压器，气体直接排至外界，背压eP 即环境压力（缓变量），认为δPe=0；根据试验结果，蓄压器内温度主要受注入气体温度和流量控制，变化缓慢，因此 gTδ =0。

联立上述各小偏差线性化等式，并做拉普拉斯变换，可以得到：

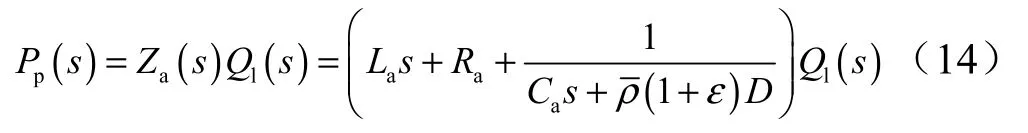
式中 D 为排气管路稳态流量与气枕压力比值，D =Qe/ Pg； Za为注气式蓄压器阻抗。

贮气式蓄压器的动特性方程为

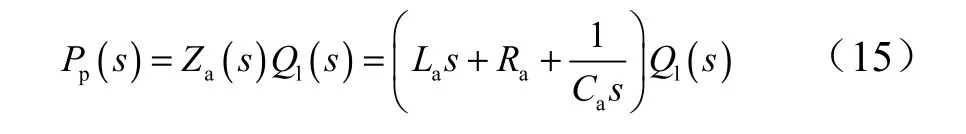
两者的区别在于，排气管路影响了注气式蓄压器动特性，本文称1 +ε) D为排气因子。

以某“水-氮气”原理性注气式蓄压器为例，气枕容积 Vg=50 L，稳态压力 Pg=0.6 MPa，环境背压Pe=0.1 MPa，排气管路等效孔径5 mm。排气稳态流量Qe=0.0275 kg/s ， 系 数 D= 0.046 ×1 0−6m ⋅ s2，1 +ε) D = 6.55 ×1 0−6m ⋅ s2。 蓄 压 器 柔 度Ca= 5.95 × 10−5m ⋅ s2。

针对系统1 Hz 以上的激励，蓄压器柔度与排气因子的相对效应为

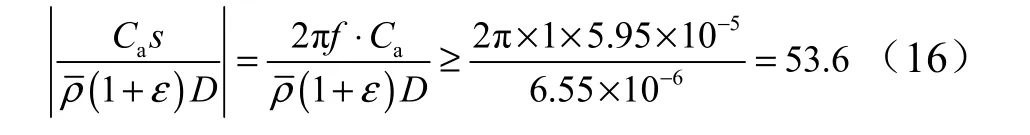
可以看出，在蓄压器柔度较大的情况下，排气管路对动特性的影响可忽略。注气式蓄压器的动特性方程形式与贮气式蓄压器一致。

2 两种蓄压器性能比对

影响蓄压器性能的参数包括蓄压器柔度、阻力和惯性等，相比于输送管的惯性，纯柔性蓄压器的惯性是小量，蓄压器阻力系数对系统动特性的影响很小，因此决定蓄压器性能的参数主要为柔度。由上文讨论可知，注气式蓄压器柔度如式（8）所示。

贮气式蓄压器的柔度可描述为

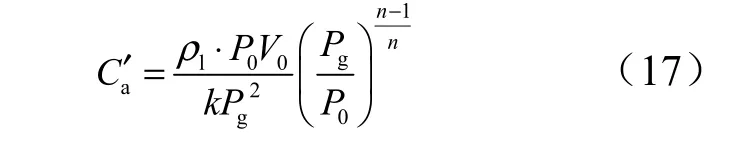
式中0P ，0V 分别为贮气式蓄压器初始气枕压力和初始气枕容积；n 为贮气式蓄压器气枕多变指数。

注气式蓄压器由于一般有限位管的作用，气枕体积gV 恒定，可以看作是定体积过程；贮气式蓄压器的体积gV 随入口压力而变，为多变过程，蓄压器入口变化不太迅速的情况下，可将其视为等温过程，即n=1。

从柔度的表达式可以看出，注气式蓄压器的柔度与入口压力成反比，贮气式蓄压器的柔度与入口压力的平方成反比，运载火箭飞行过程中过载不断增大，蓄压器入口压力一般随之增大，因此注气式蓄压器柔度受入口压力增大而衰减效应要明显低于贮气式蓄压器，具有更强的POGO 抑制能力，这就使得注气式蓄压器系统容积可以做的更小。

图3 为输送系统包括输送管路和末端的蓄压器示意，输送系统管路末端封堵，上游贮箱直径远大于输送管路直径，组成一个典型的“开-闭”系统，忽略管路阻力、蓄压器惯性和阻力，可以得到系统的一阶频率为

式中dL 为输送管的惯性， Ld=ld/ A，其中，dl 为输送管线长度。

图3 输送管+蓄压器系统示意Fig.3 Diagrammatic Sketch of a Pipe & Accumulator

对于相同的初始气枕容积，两种蓄压器柔度随着入口压力变化如图4 所示，其中，C0为蓄压器入口压力为P0时的柔度。可以看出，随着入口压力的升高，贮气式蓄压器柔度下降速率明显快于注气式蓄压器，当飞行过程中蓄压器入口压力变化范围较大时，贮气式蓄压器的柔度衰减很大，例如当压力P=2P0时，贮气式蓄压器的柔度为0.25C0，而注气式蓄压器的柔度为0.5C0。

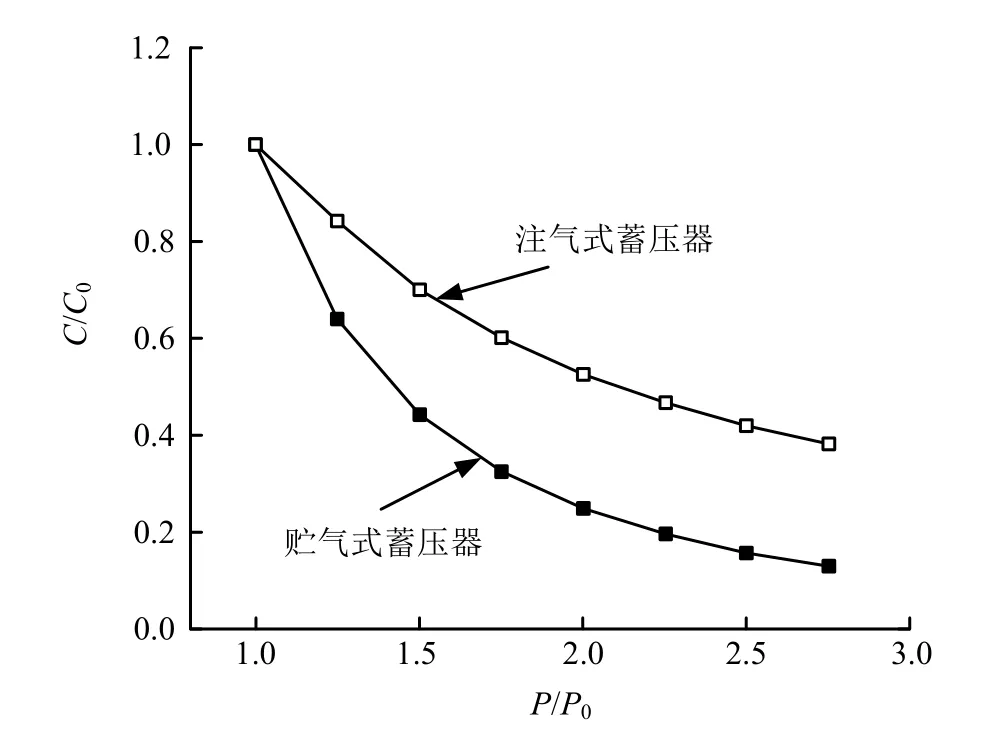
图4 注气式和贮气式蓄压器的柔度随入口压力变化Fig.4 Flexibility Variation with Inlet Pressure of Gas-injected and Gas-storaged Accumulator

随着运载火箭规模的增大，输送管路直径增加（管路惯性减小），要将输送系统频率限制在一定范围内，需要的蓄压器柔度也越来越大。火箭动力系统一阶频率通常由泵前管路（见图3）所决定，假定要将某一动力系统一阶频率降低至4 Hz 以下，两种蓄压器的气枕容积随着管径增大的变化情况如图5 所示，其中Vg0为输送管直径为D0时所需的蓄压器气枕容积。从图中可以看出，当输送管直径达到4D0倍后，对贮气式蓄压器的气腔容积需求已经达到D0直径时的15 倍以上，约为注气式蓄压器体积的2 倍。

图5 注气式和贮气式蓄压器容积随管路直径变化Fig.5 Gas volume Variation with Pipe Diameter of Gas-injected and Gas-Storaged Accumulator

综上所述，相同管路压力条件下注气式蓄压器的变频降幅能力越强；相同变频需求下注气式蓄压器气枕容积要求更小，结构效率更高。此外，注气式蓄压器相比于常见的金属膜盒式蓄压器（一种典型的贮气式蓄压器），没有膜盒焊缝疲劳强度、膜盒稳定性等问题，工艺简单可靠。

3 试验验证

为进一步验证注气式蓄压器理论预示模型的正确性，利用安装有注气式POGO 抑制系统的输送管进行了水介质动态特性试验，试验系统原理见图6。注气式蓄压器由一套地面控制器控制注气和排气的时序，供气系统提供恒定的压力源，电磁阀控制气源的通断，由孔板限制流量，排气管路通过电磁阀控制排气流量。系统的脉动由安装于管路底部的活塞式脉动压力发生器生成，通过对管路沿程脉动压力的测量，确定系统的动态特性。

图6 试验系统原理Fig.6 Schematic Diagram of Test System

3.1 定压扫频激振

在保持蓄压器入口压力恒定的状态下，激振系统做1.5～50 Hz 的扫频激振，通过管路沿程脉动压力传感器的数据可得到管路系统一阶频率的试验值，根据第1节的模型可计算出一阶频率的理论值，两者对比如表1所示。由表1 可知，计算与试验值的相对误差在8%以内。

表1 定压扫频激振的试验结果Tab.1 Test Result of Sweep Frequency Excitation with Const Pressure

3.2 飞行压力随机扫频

注气式蓄压器模型推导中假定了泵入口稳态压力变化过程不与管路内低频脉动相耦合，即蓄压器的动特性只与当前入口压力有关，而与压力变化速率无关。为了验证该假设，通过贮箱增压模拟一级飞行段注气式蓄压器入口压力，通过控制加泄管路上截止阀的开闭或者贮箱放气，模拟发动机启动过程中和助推分离时刻，蓄压器入口压力突变的工况。脉动压力发生器进行1.5～50 Hz 的宽带随机激振。

与注气式蓄压器的使用模式相对应，为防止发动机启动负水击使得蓄压器内气体涌入输送管中，发动机起动前蓄压器为无气枕状态，在发动机完成启动后，将蓄压器充气至额定容积。图7 为飞行状态下动力系统一阶频率曲线。

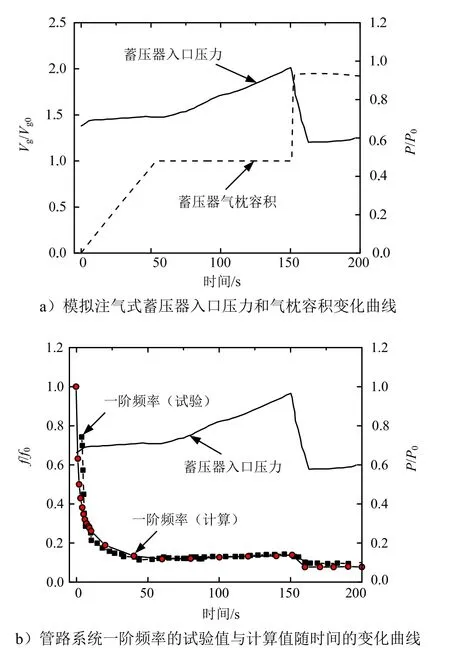
图7 飞行状态下动力系统一阶频率曲线Fig.7 First Order of Frequency of Power System in Flight

从图7 中可以看出试验数据与仿真数据的一致性良好；由于小气枕容积状态下缺少容积实测值，用理论气枕容积预测的一阶频率与试验值偏差相对较大。

4 结 论

本文对注气式POGO 抑制动力学模型进行了推导和分析，分析了注气式蓄压器和贮气式蓄压器模型上的差异，理论分析指出排气对注气式蓄压器动力学模型的影响，利用分析模型比较得出了注气式POGO 抑制方式具有抑制能力高、对安装空间要求低等优势。通过输送管路系统试验验证了注气式蓄压器线性化模型在不同压力入口条件下的正确性。