一种非电传爆系统的全局灵敏度分析研究

程 蕾，王晓鹏，夏 艳，王宇锐，范新中

（中国运载火箭技术研究院，北京，100076）

0 引 言

当前航天技术发展形势下，对非电传爆系统的可靠性要求越来越高，非电传爆系统的设计[1]、可靠性评估[2]研究工作也显得尤为重要。根据非电传爆系统传爆序列特点，利用全概率统计的思想，对这种复杂系统的可靠性进行评估，通过这种方法往往可以得到较为合理的评估结果。然而，使用全概率方法评估非电传爆系统可靠性时，是将各个传爆环节的可靠度作为输入，最后通过全概率公式得到系统可靠度。因此，要进一步提高系统可靠性，就需要对各个传爆环节可靠度的灵敏度进行分析，重点关注灵敏度高的传爆环节的可靠度，并在工程实际中落实提高重要传爆环节的可靠度，以提高系统的可靠性。

不确定性的传递过程分为2 种，正向传递和逆向传递。正向传递指输入不确定性向输出不确定性的传播问题，而逆向传递则指追溯输出不确定性向输入不确定性的分配问题。灵敏度分析即探索输入变量不确定性对输出不确定性的贡献大小，并给出输入变量的重要性排序。一旦得到重要性排序，就可以在模型分析中起到非常有效的指导作用[3,4]，协助模型分析人员以最小经济、时间代价的约束最有效地减小模型输出的不确定性。当前应用较为广泛的是Sobol 提出的全局灵敏度指标[5,6]，旨在衡量输入变量不确定性对输出模型的影响程度。众所周知的数值模拟法（Monte Carlo，MC）可以用来求解Sobol 指标[7]，单层数值模拟法（Single Monte Carlo，SMC）[8,9]则在此基础上大大节约了计算成本，本文将这2 种方法均引入到非电传爆系统的全局灵敏度指标求解中。

一旦得到非电传爆系统的全局灵敏度指标，即得到各传爆环节可靠度的重要性排序，就可以有目的地按顺序依次提高特定传爆环节的可靠度，以最小的成本、最优化的思想使得系统可靠性达标，满足航天产品的验收需求。本文给出的非电传爆系统算例给出了Sobol 全局灵敏度指标使用的流程，适用于航天工程系统内的各类非电传爆系统。

1 某非电传爆系统描述

某非电传爆系统由2 发电爆管、1 套传爆组件，4发爆炸螺栓、2 件锁紧螺母、2 件安装螺母和2 件锁紧螺母组成，系统结构示意见图1。

图1 某非电传爆系统结构示意Fig.1 Sketch of the Non-electric Detonation Transfer System

其工作原理如下：任一发电爆管通入额定电流后，起爆器工作，起爆传爆组件，导爆索传爆并通过4 路输出接头同时起爆4 发爆炸螺栓，爆炸螺栓工作，从预定分离面分离，完成预定功能。只要一路导爆索组件可靠工作，就能够保证4 发爆炸螺栓可靠分离。

系统接入一定电流后，2 发电爆管工作输出能量，起爆传爆组件歧管内装的受主装药，受主装药工作，起爆4 路集束的导爆索，导爆索传爆并起爆输出接头内装的小火帽，小火帽工作，起爆爆炸螺栓，爆炸螺栓完成分离功能。产品功能框图见图2。其中，D1～D7表示非电传爆系统各传爆单元，各单元的可靠度可用R1～R7表示，非电传爆系统的系统可靠度可用RS表示。由图2 可以看出：

a）D1～D3为冗余结构，设计为2 路并联的串联结构系统；

b）D4～D6为冗余结构，相应于每个爆炸螺栓设计为2 路并联的串联结构系统；

c）4 路爆炸螺栓为串联结构，共同完成系统的分离功能。

图2 某非电传爆系统功能框图Fig.2 Diagram of the Non-electric Detonation Transfer System

2 非电传爆系统全概率可靠性评估方法

全概率公式通常将复杂事件分解为若干不相容的简单事件之和，通过得到简单事件的概率，利用其可加性，求得系统可靠性。以图2 所示的2×4 路系统功能框图为例，下面简单介绍全概率方法评估非电传爆系统可靠性的过程。首先，对图2 中的串联过程进行合并，将系统功能框图简化后见图3。

图3 功能框图简化图Fig.3 Simplified Functional Diagram

下面采用全概率方法评估非电传爆系统的可靠度。假设A1和A2工作的可靠度分别为 RA1和RA2，RS|A1表示A1正常工作下系统正常工作的概率，表示A1失效时系统正常工作的概率。那么，系统可靠度为

根据图2 可知，要保证A1失效时系统正常工作，那么A2必须正常工作，即= 0，因此有：

继续对RS|A1进行全概率分解。假设 RS|A1A2表示 A2正常工作时正常的概率，表示A2失效时RS|A1正常的概率，那么有：

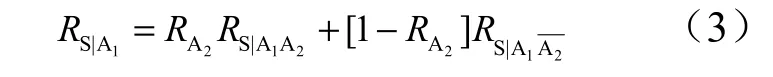
将式（2）、式（3）代入式（1），得系统可靠度为

下面分别对 RA1、 RS|A1A2、RS|A1A2建立可靠性框图，给出可靠度计算公式。

表示“电爆管发火—起爆受主装药—受主装药起爆4 根集束导爆索”过程的可靠性，即D1～D3的串联过程，那么有：

RS|A1A2表示A1、A2同时正常工作时系统工作的可靠度，对应的可靠性框图见图4。

图4 RS |A 1 A2对应的可靠性框图Fig.4 Reliability Diagram Corresponding to RS|A 1 A2

由于B 表示“导爆索传爆-起爆小火帽-小火帽起爆爆炸螺栓”的过程，即D4～D6的串联过程，C 表示爆炸螺栓分离，即D7。那么有：

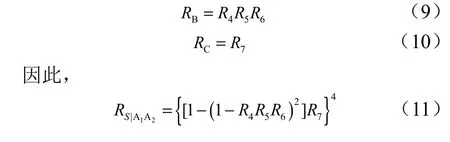
图5对应的可靠性框图Fig.5 Reliability Diagram Corresponding to

综上，非电传爆系统工作可靠度为

3 非电传爆系统全局灵敏度分析模型

3.1 全局灵敏度指标

不确定性分析领域中，结构系统分析的基本问题包括正向分析和逆向分析2 个方面。其中，正向分析研究输入变量的不确定性向输出性能的传递问题，通过结构系统中不确定性的正向传递分析，可以预测和评价输入变量的不确定性在结构系统中的行为结果，而逆向分析则研究输出性能的不确定性向输入变量的分配问题，也称为灵敏度分析，通过不确定性在结构系统中逆向的灵敏度分析，可以识别影响结构系统输出性能的输入变量重要性排序，从而对结构系统分析、预测和优化提供指导。

当前应用广泛的一个全局灵敏度指标为Sobol 基于方差的指标，即[5,10]：

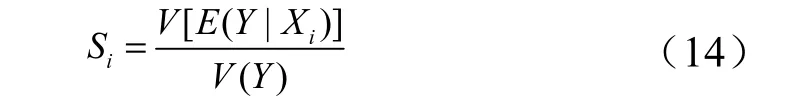
式中 V [ E (Y | Xi)]为固定某输入变量Xi时的条件期望E (Y | Xi)的方差； V (Y )为无条件输出Y 的方差。Sobol基于方差的指标 Si反映了输入变量Xi对输出响应Y 方差的贡献。

Janon[11]指出，Sobol 指标可以表示成模型的无条件输出与固定某一随机输入时的条件输出之间的协方差。这个条件输出一般可以通过固定某个特定输入变量然后对其他变量随机采样得到，也就是：

式中 Y =f ( X , Z)；YX= f ( X , Z')。X 和Y 为相互独立的随机输入变量。式（15）表明，Sobol 基于方差的指标代表无条件输出Y 与固定某一随机输入时的条件输出YX之间的协方差Cov(Y , YX)除以一个系数 V (Y )。

由于Pearson 系数定义为两变量X1和X2之间的线性相关程度

则，Sobol 基于方差的指标可以进一步表达如下：

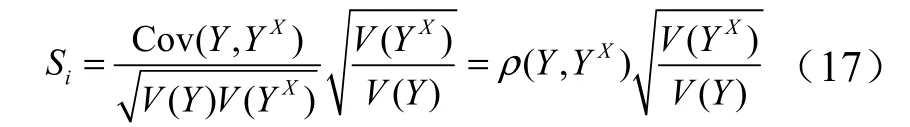
明显地，Sobol 基于方差的指标就是无条件输入与固定某输入时的条件输出之间的Pearson 相关系数乘以一个系数。

3.2 非电传爆系统全局灵敏度指标

考虑图1 中的非电传爆系统，输入变量可设为各传爆环节可靠度 Ri( i = 1,2,..., n)，功能函数则为式中的系统工作可靠度。

因此，定义非电传爆系统的功能函数为

式中 SRi为传爆环节可靠度 Ri( i = 1,2,..., n)对系统输出可靠度的影响程度，SRi越大代表 Ri的重要性越高，反之亦然。

类似式（17），灵敏度指标可以改写如下：

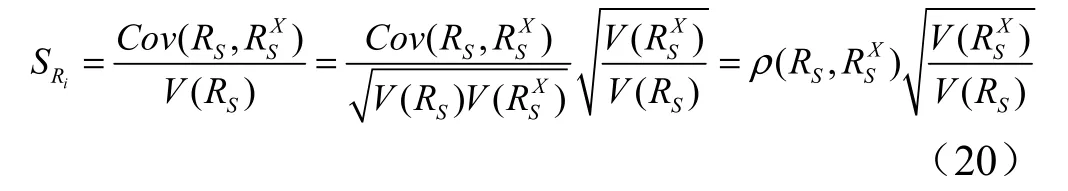
那么，非电传爆系统的灵敏度指标可以利用类似Sobol 指标的单层抽样方法进行求解。

3.3 非电传爆系统全局灵敏度指标求解

对于图1 中所示的2×4 路的非电传爆系统，要求在置信度0.95 下，非电传爆系统的可靠度不低于0.99。根据全概率评估方法，需要对各个传爆环节进行可靠性评估，如表1 所示。

表1 传爆系统各环节可靠度指标Tab.1 Reliability of Each Intermediate Link

根据式（13）中的功能函数，给定一组传爆系统各环节可靠度，得到对应的系统可靠度。下面使用SMC方法求解非电传爆系统全局灵敏度指标，步骤如下：

a）定义非电传爆系统各环节可靠度指标Ri( i= 1,2,.., n )随机取{0.99,0.999,0.9999, 0.99999,0.999999}中的值，得到输入变量矩阵 R(A)( N ×n)和( N ×n)；

b）根据输入矩阵 R(A)( N ×n)按式得到一列对应的系统输出可靠度×1)；

c）令输入变量矩阵，且 R(C)(:, i) =R(A)(:, i)，那么可以得到此时的一列系统输出可靠度；

e）将步骤c）和步骤d）重复n 次，即可得到各传爆环节可靠度的全局灵敏度指标排序。

3.4 非电传爆系统全局灵敏度指标结果

a）R1～R7随机取自集合{0.99,0.999,0.9999,0.99999,0.999999}。

随机样本量105下系统可靠度的分布如图6 所示。可以看到， 系统可靠度的变动区间大致为[0.9,0.999999]，若能识别出对系统可靠度影响较大的传爆单元并着重提高该单元可靠度，可有目的地实现系统可靠度的大幅提升。

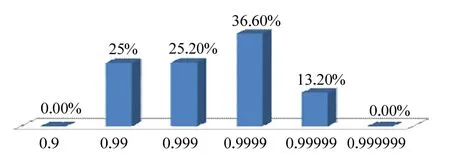
图6 样本量105 下的系统可靠度分布比例Fig.6 Distribution Ratio of the System Reliability with N=105

本文使用MC 和SMC 计算全局灵敏度指标，得到各个传爆环节可靠度的全局灵敏度指标如图7 所示。

图7 各个传爆环节可靠度对应的全局灵敏度Fig.7 Sobol’s Global Sensitivity Index of Each Intermediate Link

由图7 可知，SMC 得到的结果精度可信，且R7的重要性最高，其次为R4～R6，再次为R1～R3。若想提高系统可靠度，应重点提高传爆单元D7的可靠度R7。

b）R1～R6随机取自集合{0.99,0.999,0.9999,0.99999,0.999999}，R7固定在集合中任一值。

使用MC 和SMC 分别计算全局灵敏度指标，结果如图8 所示。

图8 R7 固定时各个传爆环节可靠度对应的全局灵敏度Fig.8 Sobol’s Global Sensitivity Index of Each Intermediate Link with Fixed R7

由图8 可以看出，SMC 方法所得结果的精度可信，且各环节可靠度的重要性排序为R4～R6>R1～R3。

当固定 R7为集合{0.99,0.999,0.9999,0.99999,0.999999}中任一值时，通过MC 方法可以统计得到规律如下：

a）当R7取0.99 时，由于图7 中显示R7的重要性远远大于R1～R6，因此无论如何调节R1～R6，RS均不能达到0.99。

b）进一步提高最重要环节可靠度，即R7取0.999时，由表2 可以看出RS可在一定条件下可以达到0.99。若R1～R6均为0.99，那么RS为0.9。由于图7 中显示R4～R6的重要度高于R1～R3，那么优先提高R4～R6，可以得到表2 中的结果。

表2 R7 取0.999 时对应的一系列RS 结果Tab.2 Results of RS with R7=0.999

依据表2 可以看出：

1）在第一行R1～R6均为0.99 的基础上，改变输入环节可靠性满足如下任一条件，均可以将 RS提高到0.99。R4～R6中至少有2 个满足0.999；R1～R3和R4～R6中各有一个满足0.999； R1～R3均为0.999。

2）不论如何调节R1～R6，RS均不能达到0.999。

由以上分析可以得出，在 R7一定的条件下，在R1～R3保持不变的条件下将R4～R6其中两个由0.99 提高到0.999，即可以将RS由0.9 提高到0.99；而在R4～R6保持不变的条件下需要将R1～R3均提高到0.999，才可以将RS由0.99 提高到0.999。此结果与图8 中R4～R6重要性大于R1～R3的分析一致。

c）当R7取0.9999 时，若R1～R6均为0.99，那么RS为0.9。由于R4～R6的重要度高于R1～R3，优先提高R4～R6的可靠性，可以得到表3 中的结果。

表3 R7 取0.9999 时对应的一系列RS 结果Tab.3 Results of RS with R7=0.9999

由表3 可以看出：在第1 行R1～R6均为0.99 的基础上，提高任一输入环节可靠性，均可以将RS提高到0.99；至少要满足如下条件，才可以使RS达到0.999。R4～R6均为0.999，R1～R3中至少有2 个达到0.999。不论如何调节R1～R6，RS均不能达到0.9999。

由以上分析可以得出，在R7为0.9999 时，将R1～R6任一个提高到0.999，均可实现将RS由0.9 提高到0.99，这与表2 中3～4 行结果（R7为0.999 时需提高R1～R6中的两个才可实现将RS由0.9 提高到0.99）形成对比，再次证明了R7的重要性最高。而表3 中第4 行也再次证明了R4～R6重要性大于R1～R3。

d）当R7取0.99999 时，若R1～R6均为0.99，那么RS为0.9。由于R4～R6的重要度高于R1～R3，优先提高R4～R6的可靠性，可以得到表4 中的结果。出：

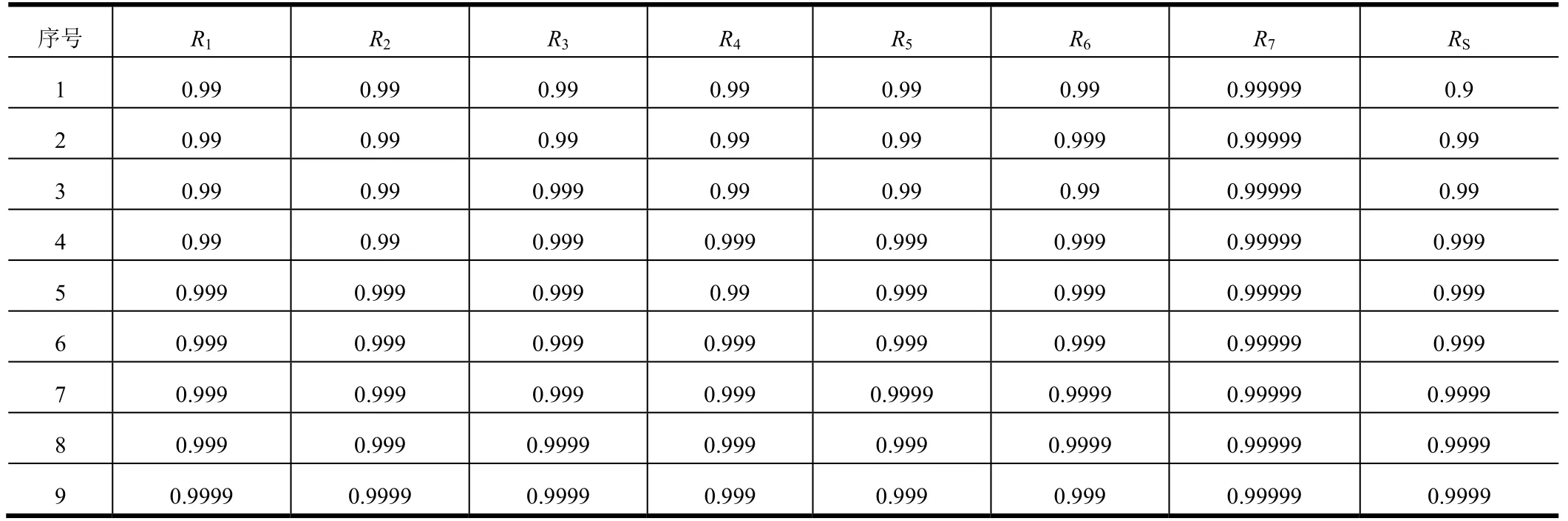
表4 R7 取0.99999 时对应的一系列RS 结果Tab.4 Results of RS with R7=0.99999

依据表4 可以看出：

1）在第1 行R1～R6均为0.99 的基础上，提高任一输入环节可靠性，均可以将RS提高到0.99；2）至少要满足如下任一条件，才可以使RS达到0.999。

（a）R4～R6均为0.999，R1～R3中至少有一个达到0.999；（b）R1～R3均为0.999，R4～R6中至少有两个达到0.999。

3）若R1～R6均为0.999，那么RS依然为0.999。在此基础上，至少要满足如下任一条件，才可以使RS达到0.9999。

（a）R1～R6中至少有2 个达到为0.9999；（b）R1～R3和R4～R6中各有一个满足0.9999；（c）R1～R3均为0.9999。

4）无论如何调节R1～R6，RS均不能达到0.99999。

由以上分析可以得出，表4 中2～3 行与表3 中2～3行结果一致；表4 中4～6 行与表3 中4 行形成对比，在将R7由0.9999 提高到0.99999 时，有多种方案可使得RS由0.99 提高到0.999，再次证明了R7的重要性最高；而表4 中7～9 行的结果，再次证明了R4～R6重要性大于R1～R3。

e）当R7取0.999999 时，若R1～R6均为0.99，那么RS为0.9。由于R4～R6的重要度高于R1～R3，优先提高R4～R6的可靠性，可以得到表5 中的结果。依据表5 可以看

1）在第一行R1～R6均为0.99 的基础上，提高任一输入环节可靠性，均可以将RS提高到0.99；

2）至少要满足如下任一条件，才可以使RS达到0.999。

（a）R4～R6均为0.999，R1～R3中至少有一个达到0.999；

（b）R1～R3均为0.999，R4～R6中至少有2 个达到0.999。

3）若R1～R6均为0.999，那么RS依然为0.999。在此基础上，R1～R6中任一个满足0.9999，那么RS就可以达到0.9999。

4）至少要满足如下条件，RS可达到0.9999。R4～R6均为0.9999，R1～R3中任意2 个达到0.9999。

由以上分析可以得出，表5 中2～3 行与表3 中2～3行结果一致；表5 中4～6 行与表4 中4 行结果一致；表5 中7～8 行与表4 中7～9 行形成对比，在将R7由0.99999 提高到0.999999 时，将R1～R6任一个提高到0.9999，即可使得RS由0.999 提高到0.9999；而达到表5 中第9 行条件时，即可使得 RS由0.9999 提高到0.99999。

表5 R7 取0.999999 时对应的一系列RS 结果Tab.5 Results of RS with R7=0.999999

4 结 论

本文根据非电传爆系统的传爆特点，利用当前应用广泛的全概率分析方法对非电传爆系统的可靠性进行合理评估，将Sobol 全局灵敏度指标推广到非电传爆系统，并应用MC 和SMC 分别进行求解，得到各传爆环节可靠度对系统可靠度指标的重要性排序。根据所得重要性排序，在非电传爆系统可靠度评估中可以首先调整最重要环节的可靠度，然后依次调节次重要环节的可靠度，最终实现有目的地、最小成本地提高非电传爆系统的可靠度，满足火工品的验收要求。