挠性航天器刚性-柔性耦合系统动力学建模研究

张恒浩，刘 涛，刘 焱，曾 洁，张雨佳

（1. 中国运载火箭技术研究院研究发展中心，北京，100076；2. 中国运载火箭技术研究院，北京，100076；3. 首都航天机械有限公司，北京，100076；4. 中国航天系统科学与工程研究院，北京，100048）

0 引 言

在早期的航天器发展过程中，刚体动力学模型能够准确反应航天器的动力学特征[1,2]。但是随着航天技术的快速发展，航天器种类越来越多，而且航天器根据任务要求搭载的挠性附加载荷种类和数量也越来越多（例如太阳能帆板、空间机械臂、大尺寸柔性天线等）[3～7]。当航天器进行大范围、大角度姿态的运动时，运动过程中航天器携带的柔性附加载荷产生的弹性变形效果开始影响航天器运动，同时开始和航天器刚性体本身产生耦合干扰[8,9]。传统的航天器动力学模型采用零阶动力学近似模型，在设计过程中忽略了大运动过程中航天器刚性-柔性耦合干扰和挠性部件弹性变形[10]。但是航天器在进行大范围、大角度机动时，特别是在高速运动中，表现出来的动力学真实情况与附加载荷的变形及刚性-柔性耦合干扰有很大关系[11～14]。1987 年，Kane 提出了动力学刚化概念，自此，许多学者开始研究动力学刚化问题并分析研究相应的动力学模型。引入动力学刚化并研究分析刚性-柔性耦合特性的动力学运动模型具有非常重要的工程应用意义[15]。

现阶段，引入动力学刚化分析的挠性航天器刚性-柔性耦合系统组合体的动力学模型研究有2 个关键点需要考虑：

a）动力学建模应考虑刚体运动特性和柔性部件变形影响，并分析这二者之间的耦合干扰作用；

b）动力学刚化特征应包含在动力学模型中。

因此综上所述，挠性航天器刚性-柔性耦合系统的动力学系统研究主要存在如下难点：

a）动力学耦合系统的方程阶数太高，并且建模过程太过复杂，不利于数学计算；

b）处理动力学刚化问题时，不仅需要通过挠性部件横截面的变形场高阶扩展项获得动力学刚化项，还需要从物理原理的理论上说明产生动力学刚化的原因[16]。

针对上述研究难点，本文首先建立一个挠性航天器刚性-柔性耦合的动力学模型，该模型由中心刚体和挠性梁2 个子系统组成，中心刚体子模型采用材料力学定理进行连续动力学建模；挠性梁子模型采用角动量定理进行连续动力学建模。然后通过挠性梁固有振荡约束模态的正交化理论建立整体的空间立体状态模型。最后通过仿真验证本文提出的航天器刚性-柔性耦合动力学模型。仿真结果表明，考虑动力学刚化的一阶模型能够准确显示出挠性航天器大范围运动的动力学特征。具有清晰的建模思路、简练的数学表示和很好的集中收敛性。

1 非惯性坐标系下连续动力学建模

1.1 刚体挠性耦合物理模型

刚体挠性耦合物理模型如图1 所示。这一模型可以对大型附加载荷的航天器进行建模，由一个中心刚性体和一根挠性梁组成，挠性梁连接在中心刚性体上。研究过程中设挠性梁具备Eulor-Bernoulli 特点，在空间工作时变形和应力应变较小。并且认为挠性梁的组成材料密度均匀，且梁内各个方向受力性能相同。

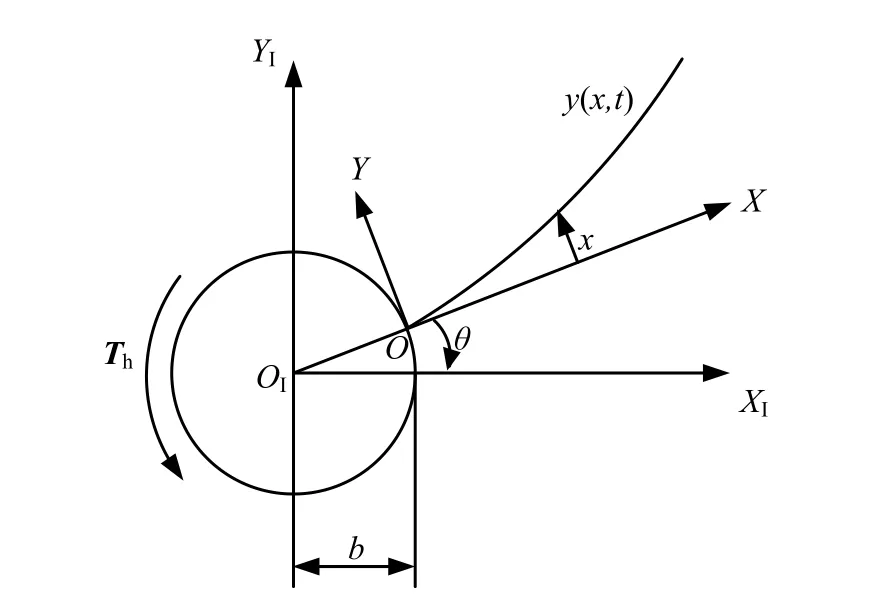
图1 刚体挠性耦合物理模型Fig.1 Rigid Physical Model with Flexible Coupling

图1 中， OIXIYI以中心刚性体的中心点为原点，OXY 建立在挠性梁上，挠性曲线 y =y （ x ,t）表述挠性梁的横向变形运动。

1.2 基于结构力学的挠性梁建模

航天器在做大范围、全姿态运动时，运动过程中挠性梁的变形过程如图2 所示。

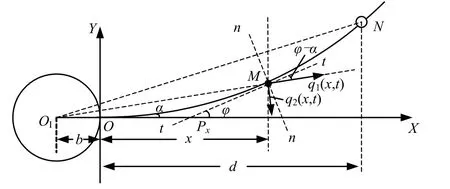
图2 挠性梁在航天器大范围全姿态运动过程中的变形示意Fig.2 Beam’s Transform with Aero-craft’s Large-scale Motion

由图2 可知，航天器在大范围运动过程中，移动坐标系OXY 是1 个非惯性坐标系。所以挠性梁横向振动的动力学特性建模研究的目的是解决在非惯性坐标系下的经典物理力学问题。通过结构力学分析可知，挠性梁的横向振动由梁自身从外部携带的分布载荷决定，这些载荷垂直安装在挠性梁上。挠性梁的横向振动动力学方程如式（1）所示：

式中 q （ x ,t ）为垂直安装在挠性梁上的载荷对梁施加的作用力；ρb为梁的密度；E 为梁的杨氏弹性系数；I为梁的横截面的旋转惯量。

如图2 所示，考虑在梁上任意位置M 上不同的质量元素 ρbdx的影响。设位置M 的坐标是 M （ x , y （ x ,t ）），位置N 的横坐标是 N （ x ,0）。OIM 的瞬时长度如式（2）所示。

在运动过程中，中心刚性体会将惯性力施加到挠性梁上。假设挠性梁上的质量单元瞬间运动沿虚线nn的方向。通过理论计算可知，科氏作用力将会分布在虚线tt 的方向上。由于科氏作用力的方向在垂直于挠性梁施加作用力的方向上分量为零，因此科氏作用力不会引起梁的横向振动，即对梁产生横向振动的力只有离心惯性力 q1（ x, t ）和切向惯性力 q2（ x ,t ），计算方程组如式（3）所示。

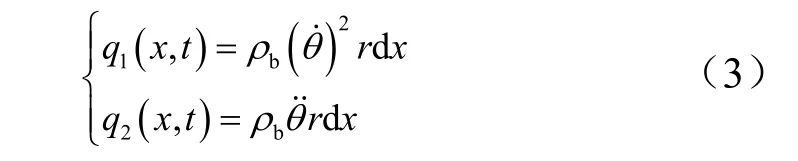
将式（3）代入式（1），外部垂直安装的分布载荷在挠性梁上的作用力如式（4）所示：

假设存在极小的位移误差和角度误差，根据图2所示的几何力学关系对梁进行受力分析。为保证工程应用，将三角函数的二阶解算项忽略。外部垂直安装的分布载荷在挠性梁上的作用力的计算如式（5）所示。

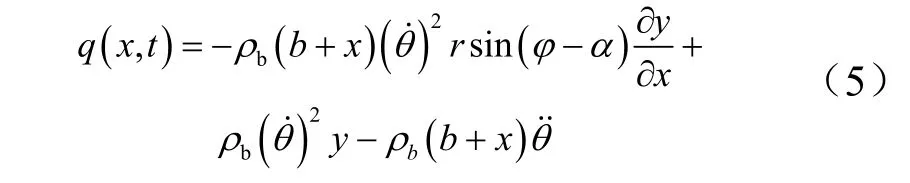
将式（5）代入式（1）中，可到挠性梁在大范围机动条件下的连续动力学模型，如式（6）所示。

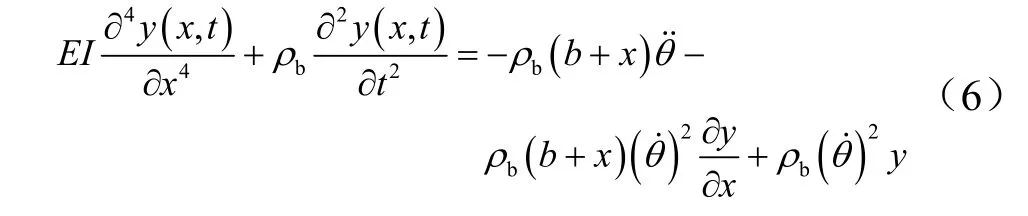
1.3 基于角动量理论的中心刚性体建模

中心刚性体在进行姿态运动时，所引起的外加作用力如图3 所示。

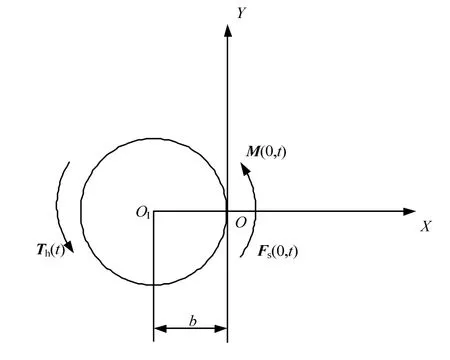
图3 中心刚性体外加作用力示意Fig.3 Forces and Torques in Addition on Hub

在分析挠性梁振动过程中，必须考虑惯性负载的影响，惯性负载是分布搭载载荷的一部分，用表示，考虑惯性负载的分布载荷作用力垂直作用于挠性梁时，其计算如式（7）所示。

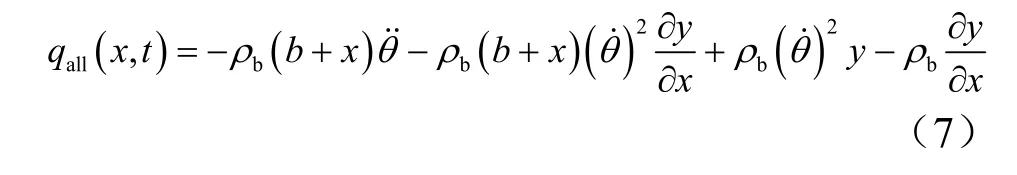
挠性梁上分布的剪切力 Fs（ x ,t ）和瞬间力矩 M（ x ,t）的计算如式（8）所示。

联立式（7）和式（8），得到中心刚性体的连续动力学模型表达式，计算过程如式（9）所示。

2 基于正交理论的离散动力学建模

用于近似描述挠性梁的横向振动变形采用展开的N 阶正交方程式，计算如式（10）所示。

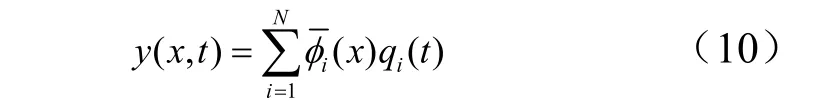
式中 φi( x)表示第i阶正交约束模态； qi(t )表示对应的模态坐标信息。挠性梁的正交约束模态的细化计算如式（11）所示。

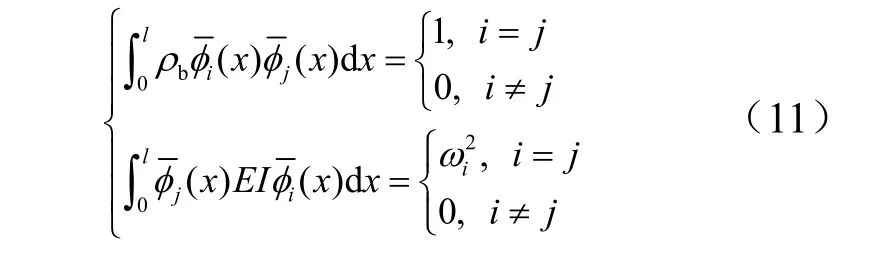
通过式（11）计算，得到挠性梁在有限空间的动力学方程：

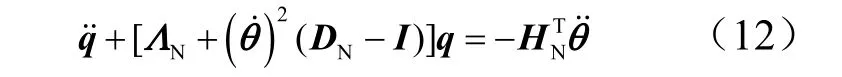
式（12）中，参数q、NΛ 、DN和HN的计算通过式（13）～（16）得到。

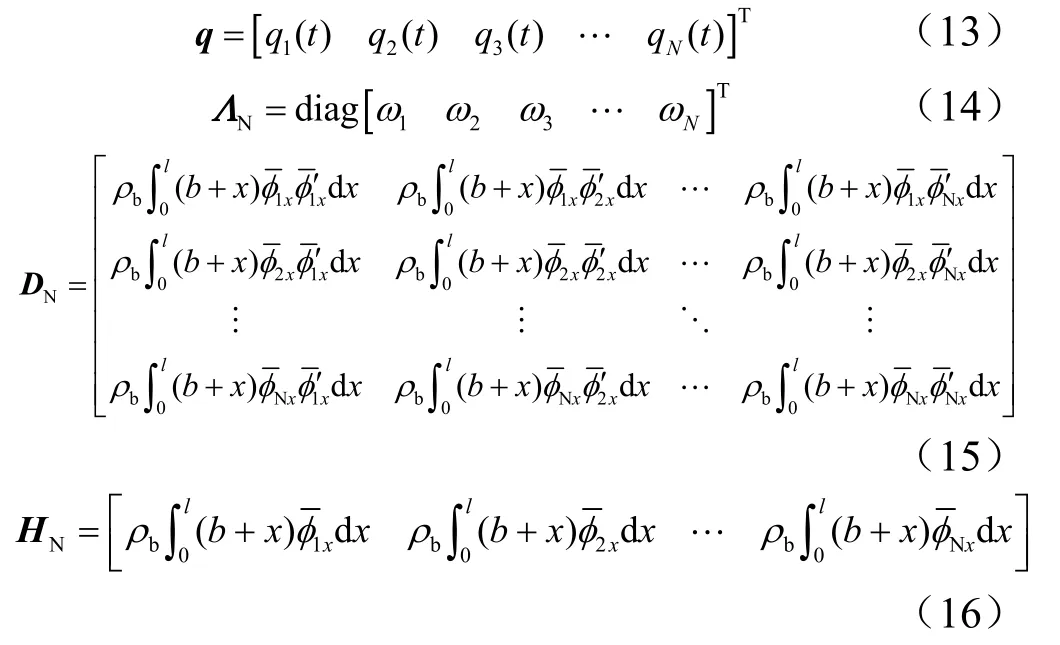
在式（12）中，挠性梁的刚性矩阵的表达式为ΛN+ （）2( DN-I )。当中心刚性体的旋转角速度发生变化时，表示挠性梁刚性矩阵计算的表达式也会发生变化，若只考虑变量参数 - （）2I ，则挠性梁刚性矩阵的计算表达式可以表述为 ΛN-（）2I，且可能发生动力学软化现象，当中心刚性体旋转时的角速度达到某一数值时，刚性矩阵开始出现负定现象，这将导致仿真计算出现误差。当全面考虑参数项（）2( DN- I )的影响时，挠性梁刚性矩阵的计算表达式表述才为 ΛN+ （）2( DN-I )，参数项（）2DN可使挠性梁的刚性矩阵具有正定性，可使仿真计算在大范围机动条件下保持收敛性。

因此上述分析即为动力学刚化现象发生的理论分析。两种情况经常出现在动力学的零阶模型和一阶模型的分析过程中。通过上述分析，中心刚性体的有限元动力学方程为

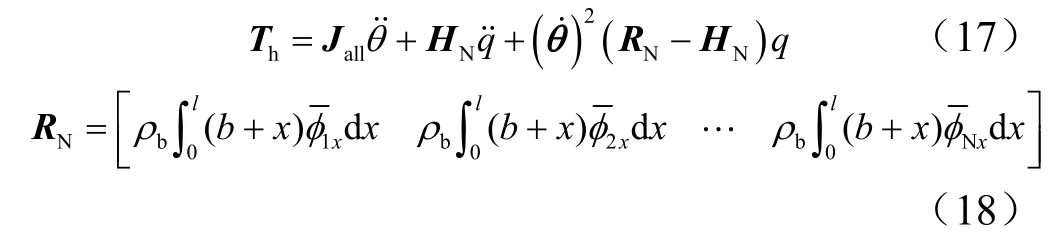
由式（12）～（18）组成挠性航天器在N 维空间的耦合动力学模型，考虑动力学刚化影响，这种耦合动力学模型能够很好地满足航天器刚性-柔性耦合组合体的大范围机动要求。整个航天器系统的状态空间方程为

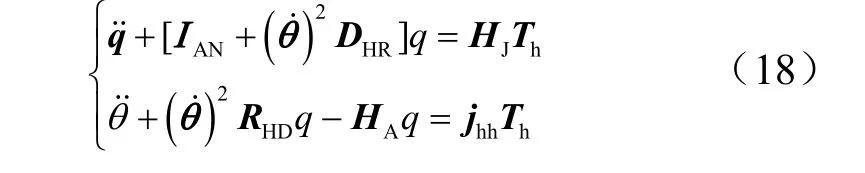
式中 IAN为中心刚体在浮动坐标系下转动惯量；DHR为惯量转动矩阵；HJ为Heaviside 脉冲函数矩阵；jhh为坐标系间转动惯量转换向量；RHD为施加力；HA为施加力矩。

各个参数的计算方程为

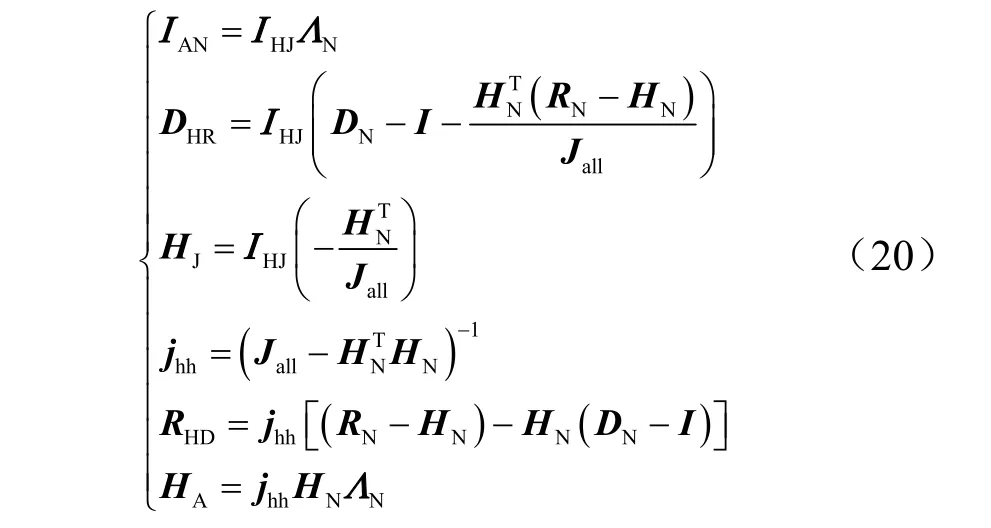
式（19）是挠性航天器刚性-柔性耦合系统在N 维空间中建立的动力学方程。当考虑动力学刚化影响时，变量参数˙θ 和q 会相互影响。挠性航天器的动力学模型从一维线性系统向非线性系统转变，因此控制系统在工作时应针对非线性特点进行相应调整控制。

3 仿真验证

为验证本文提出的挠性航天器刚性-柔性耦合系统的动力学模型的有效性，需要通过以下2 个方面进行仿真验证：

a）在航天器做已知的大范围机动过程中，采用本文模型对其引起的动力学刚化效果进行验证。

b）在航天器做未知的大范围机动过程中，分析本文一阶动力学模型在刚化影响下的收敛性。

3.1 模型动力学刚化效果验证

根据工程项目要求，设挠性航天器的相关参数为：挠性梁长度8 m，梁的弹性系数为6.8952×1010N/m2，挠性梁与刚性体的连接点面积为7.2968×10-5m2，梁材料密度为2.7667×103kg/m3，梁横截面的旋转惯量为8.2190×10-9，中心刚性体的半径为0.5 m，旋转惯量为300 kg/m2。已知的航天器大范围机动数学表述如式（21）所示。

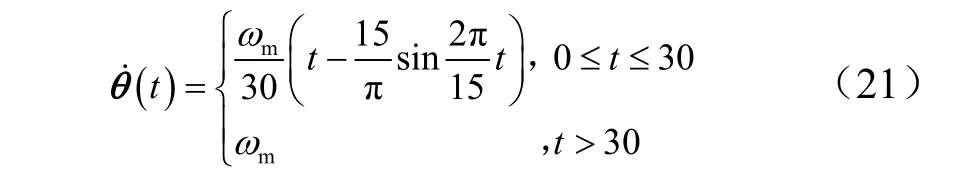
式中mω 为中心刚性体最终运动的角速度。

将中心刚性体的角速度mω 分别设为0.5 rad/s，2 rad/s和4 rad/s，分别在动力学零阶模型（Zero-order Dynamic Model，ZDM）和动力学一阶模型（First-order Dynamic Model，FDM）中进行仿真验证，结果如图4 所示。

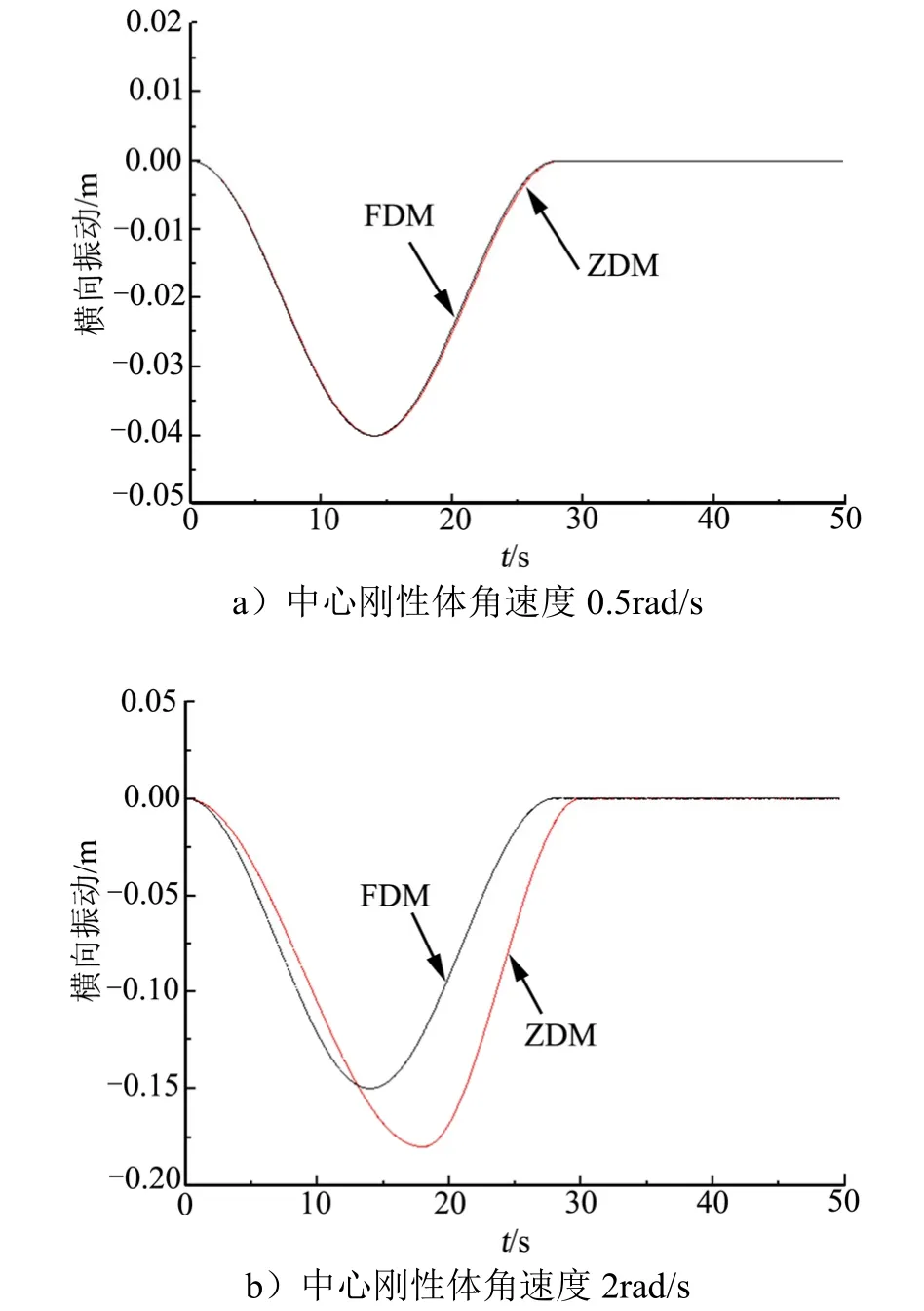
图4 挠性梁顶端横截面振动Fig.4 Beam’s Tip Transverse Deformation

续图4

如图4a 所示，当中心刚性体的角速度为0.5 rad/s时，挠性梁运动时产生的振荡频率发生偏移，此时，ZDM 模型的刚性矩阵 ΛN- （）2I 和FDM 模型的刚性矩阵 ΛN+ （）2（ DN-I ）通过刚性矩阵中的参数矩阵ΛN实现正定控制作用。因此ZDM 模型和FDM 模型均可通过控制参数矩阵ΛN实现对挠性梁横向振动的有效控制。因此两种模型在仿真过程中能够很好地对挠性梁的横向振动进行控制。

如图4b 所示，当中心刚性体的角速度为2 rad/s时，挠性梁运动时产生的振荡频率会接近其自身固有的一阶振荡频率。此时在ZDM模型的刚性矩阵和FDM模型的刚性矩阵中，参数 - （）2I 和（）2（ DN-I ）开始起正定控制作用，因此ZDM 模型需要通过控制参数- （）2I 实现对挠性梁横向振动的有效控制，而FDM 模型需要通过控制参数（）2（ DN-I ）实现对挠性梁横向振动的有效控制。这解释了ZDM 模型和FDM 模型在仿真计算过程中出现了较大差别。由图4b 可知，ZDM模型的振荡误差要大于FDM 模型，在2 rad/s 的角速度条件下，FDM 模型能够更好地抑制动力学刚化现象对挠性梁横向振动的干扰。

如图4c 所示，当中心刚性体的角速度为4 rad/s时，挠性梁运动时产生的振荡频率介于其一阶自然振荡频率和二阶自然振荡频率之间。此时，在ZDM 模型的刚性矩阵中，ΛN- （）2I 起负定控制作用，说明ZDM模型已经无法有效控制梁的横向振动，横向振动出现发散现象。在FDM 模型中，由于有参数DN能够实现正定控制，因此FDM 模型的刚性矩阵 ΛN+ （）2（ DN-I）仍然可以在大范围机动条件下保持矩阵控制的正定性。由图4c 可知，在角速度4 rad/s 的条件下，FDM模型对挠性梁的横向振动仍然收敛可控。

综上分析可知，随着中心刚性体最大角速度 ωm的增大，ZDM 模型系统的控制能力开始失效。中心刚性体角速度mω 越大，动力学刚化效果越明显，但即使当中心刚性体的角速度非常大时，FDM 模型仍然能够通过刚性矩阵有效控制动力学刚化干扰并实现收敛控制，因此FDM 模型系统能够有效解决动力学刚化现象对整个系统的影响，满足实际的工程应用要求。

3.2 FDM 模型的收敛控制分析

根据工程项目要求，设挠性航天器的相关参数为：挠性梁长度5 m，梁横截面的旋转惯量为1.333×10-8kg/m2，梁材料密度为2.7667×103kg/m3，梁的弹性系数为6.8952×1010N/m2。忽略中心刚性体的外部影响，Jstar为0，b 的值也为0。挠性梁外部转矩的计算为

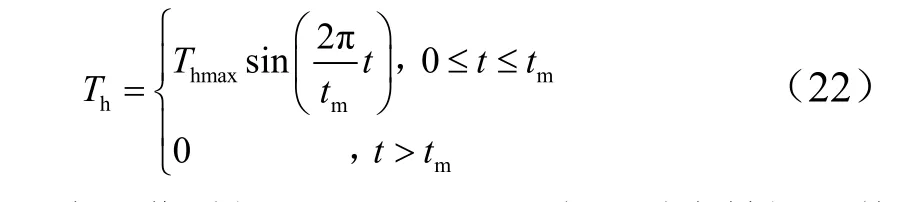
式中 tm为工作时间，取2 s； Thmax表示最大转矩，其数值为50 N·m。

图5 为挠性梁FDM 模型仿真计算结果。仿真过程中，外部最大转矩为50 N·m，挠性梁顶端横截面的最大振幅约为0.42 m。当系统到达稳定状态时，挠性梁的连续振动振幅约为0.04 m。

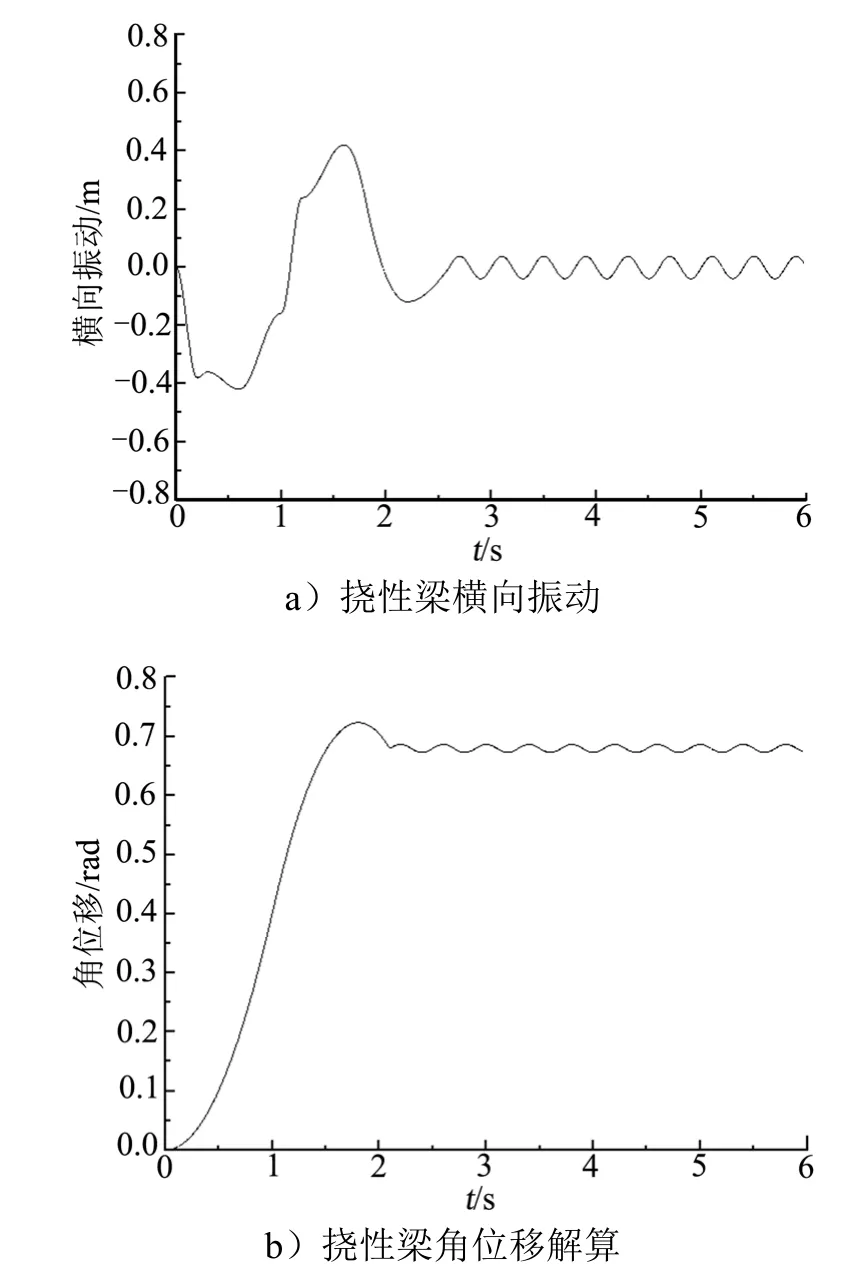
图5 一阶模型仿真解算结果Fig.5 The FMD’s Model Simulation Results

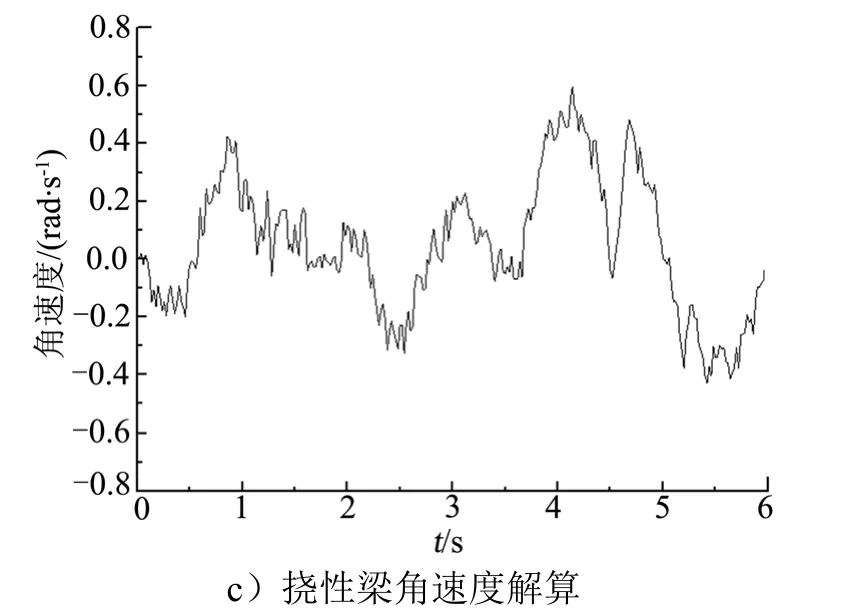
续图5

由图5 可知，尽管中心刚性体的转矩数值非常大，FMD 模型通过控制解算得到的梁横向振幅、角位移及角速度仍会有效收敛。说明FMD 模型对刚性-柔性耦合的动力学系统产生的刚化干扰具有很好的控制性能，能够较好实现控制收敛性。

4 结 论

本文研究并建立了一种挠性航天器刚性-柔性耦合系统动力学模型。该方法首先将力学理论应用在非惯性坐标系中，然后通过设计2 个子系统全面分析考虑动力学刚化影响下的航天器动力学特征并进行相关控制仿真验证。在整个模型的设计分析过程中，得到如下研究成果：

a）建立挠性梁分系统动力学模型和中心刚性体动力学模型，并进行简化处理，使其能够反映挠性梁柔性变形对航天器的影响。

b）在非惯性坐标系中引入力学理论，将动力学刚化现象与动力学运动有机联系在一起进行控制分析。

c）提出了一种动力学刚化效果理论分析及控制方法。分析得出航天器系统的动力学刚化问题耦合影响原因并处理方法。