考虑视场角的飞行时间和末端倾角控制导引律

康 珅，赵 洪，卜奎晨，高 峰，钟婧佳

（中国运载火箭技术研究院，北京，100076）

0 引 言

近年来随着飞行器性能的提升，对飞行器航迹规划的要求日益提高，某些特殊场景中，既要求飞行器从特定的方向到达目标点，又希望控制飞行器的飞行时间。针对多约束航迹规划需求，本文重点研究视场角受限情况下的飞行时间和末端倾角控制导引律。

相对于分别研究末端两项运动学约束的文献，针对同时满足飞行时间和末端倾角约束的导引律研究相对较少。文献[1]、[2]中提出的方法采用相似的多约束导引律设计思路，首先设计最优末端倾角控制导引律，之后估计该导引律的飞行时间，再根据估计飞行时间与期望飞行时间之差进行反馈，形成飞行时间控制回路。文献[3]设计了二阶滑模控制律用于跟踪期望的视线角曲线，并对视线角曲线进行航迹成型设计，从而同时满足了飞行时间和末端倾角约束。文献[4]采用弹目距离扩展多项式生成导引指令，并通过线性化模型将期望约束与多项式系数关联从而求解系数表达式。文献[5]采用滑模导引律跟踪虚拟目标的方法实现了对移动目标点的飞行时间和末端倾角约束导引。

本文采用任意阶时间多项式设计前置角变化曲线并将飞行时间和末端倾角约束转化为多项式边界条件，形成了带有飞行时间和末端倾角约束的导引律，相比现有文献中方法，主要有如下优点：a）飞行控制总消耗更接近最优解；b）用户可调参数物理意义明确；c）导引律结构简洁，有利于实现视场角约束。

1 问题描述

本文考虑二维质点运动，以纵向平面为例，考虑飞行器M 和目标点T ，二者相对运动关系如图1 所示。

图1 飞行器-目标点相对运动几何关系示意Fig.1 Engagement Geometry of Planar Guidance

飞行器法向加速度a 垂直于飞行器速度矢量，不改变其数值大小V 。前置角ε 与视线角、倾角之间的关系可表示为

则飞行器的运动可由如下微分方程描述：

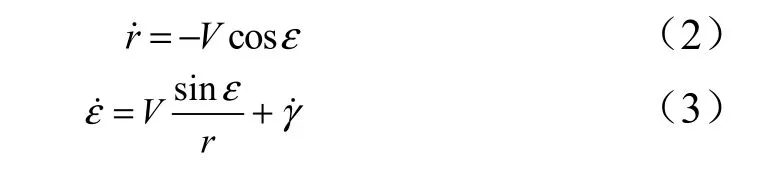
式中 r 为飞行器至目标点相对距离。

本文探讨飞行时间和末端倾角约束导引律，设计导引律控制飞行器以期望的倾角、在期望的飞行时间到达目标，即设计导引指令γ˙，对于给定的期望倾角 γd和期望飞行时间 td，当且仅当t = td时有r= 0，且同时满足 γ = γd。

2 前置角多项式与导引指令

本文采用时间多项式设计前置角变化规律。由于所处理的问题带有末端倾角和飞行时间两个隐式约束，因此提前预留两个多项式系数进行用于满足该约束，将前置角变化规律定义为n+2 阶时间多项式：

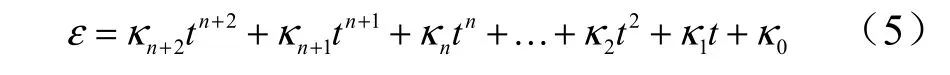
式中 n 为正整数； κn+2,κn+1, …κ0为待定系数。为确定这些系数，需给出适当的边界条件。首先式（5）必须满足前置角初始条件，即：

式中iε 为前置角初始值。其次，为保证命中目标，需定义前置角终端条件：

除去飞行时间和末端倾角预留的两项系数和边界条件式（6）、式（7），式（5）中剩余n −1 个系数待定，因此补充前置角终端条件如下：

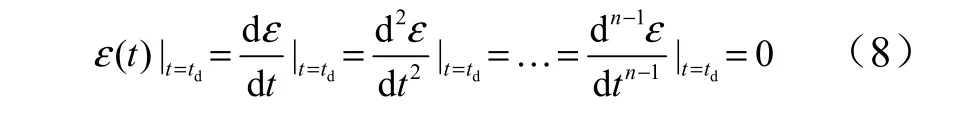
至此，除可确定n+ 2阶多项式中n 个系数，剩余2 个用于满足期望约束。由式（1）可知，可以通过量测获得时，生成导引指令γ˙仅需要前置角变化率。考虑式（5）对时间的导数，并认为和，将其改写为闭环形式：

显然为得到ε˙需确定 κ1。将多项式最高阶项系数κn+2和次高阶项系数κn+1视为自由系数，用于控制飞行时间和末端倾角。则将边界条件代入式（5）得到闭环前置角变化率与多项式阶数n 的关系，应用数学归纳法得到：

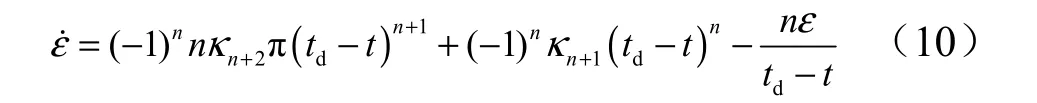
式中 td为期望命中时间。

式（10）对时间积分，并代入初始条件式（6）得到前置角函数为

为控制飞行时间以及末端倾角，后续步骤需上述两约束确定式（11）中的系数κn+1和κn+2，即导引系数。

3 导引律设计

3.1 线性化导引系数

线性化导引模型需要假设飞行器速度在水平方向上恒定不变，飞行器仅在垂直方向进行修正机动，如图2 所示。

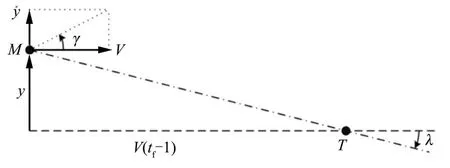
图2 线性化导引模型示意Fig.2 Linearized Engagement Geometry

定义y 为垂直偏差，则倾角与视线角可表示为

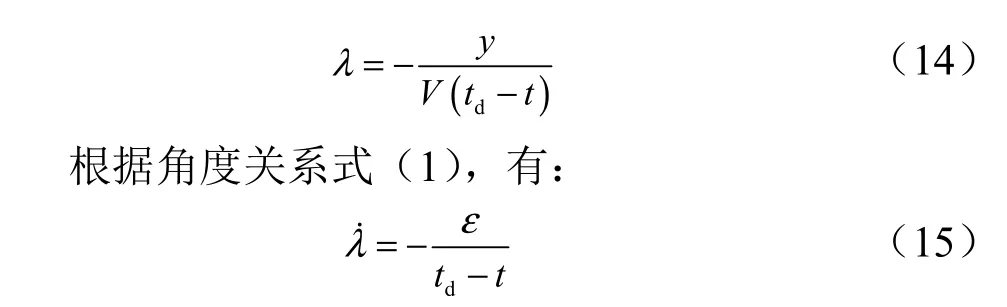
综合式（11）、（13）～（15），并令t =td可得到倾角表达式为

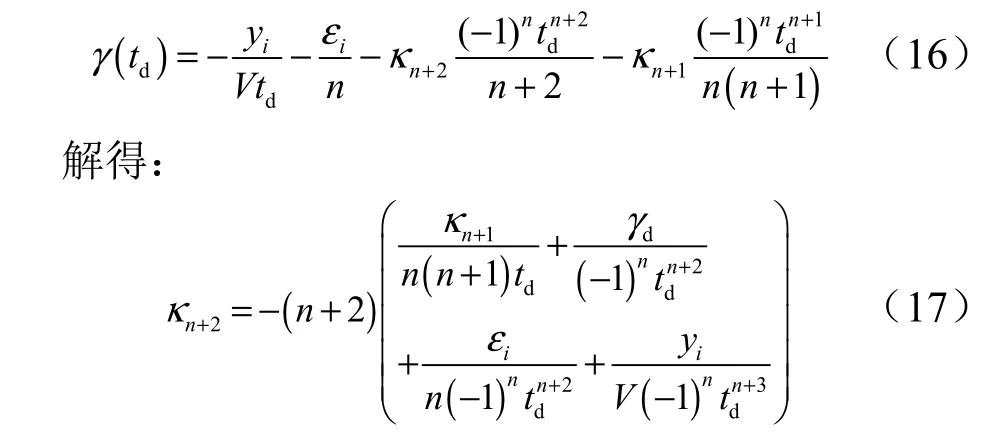
上式准确表达了线性化模型中的末端倾角约束。继续建立飞行时间约束方程并确定κn+1。

将飞行轨迹长度表示为

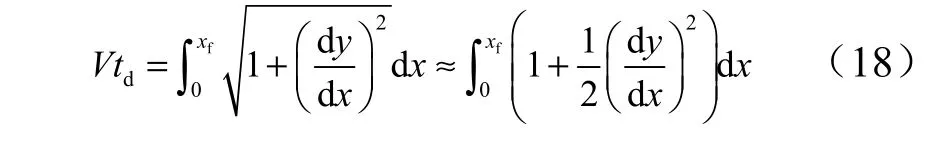
式中 xf为距离目标点的水平长度。之后假设飞行时间与水平距离线性相关，可解得：

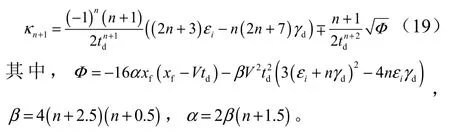
综上，κn1+和κn+2确定后，前置角多项式（5）中所有系数均确定。

3.2 导引系数更新

对于准确描述实际问题的非线性导引模型，直接应用经过上述简化计算而得出的结果，难免引入线性化误差，对各项导引控制品质造成负面影响，导致导引精度降低。因此本节中给出导引系数κn1+和κn+2的在线更新方法。

考虑当前时刻视线坐标系中的距离关系，有：

以当前时刻为时间零点，则期望的飞行时间应扣除已飞行时间，有：

同时，以当前时刻飞行器各状态的当前值替换初始值：

期望的末端倾角应变换至当前视线坐标系，根据角度关系有：

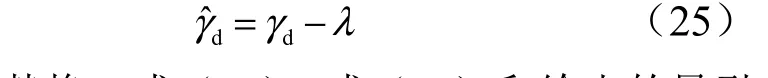
应用上述替换，式（19）、式（17）和给出的导引系数可改写为

可解得以当前状态更新的导引系数κn+1和κn+2，从而使导引律式（12）闭环。

4 仿真结果

4.1 视场角约束设置

本文认为飞行器攻角相对于前置角较小，将飞行器视场角约束近似为航迹前置角约束。给出如下切换条件用于实现视场角约束：

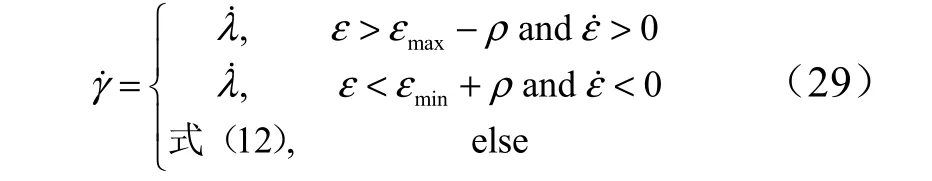
其中ε˙由式（10）计算得到。式（29）的物理意义如图3 所示，当前置角的值进入宽度为ρ 的限制区域内，并且有继续发散的趋势，将前置角的变化律置零，导引指令退化为；当前置角变化率趋于收敛，允许式（12）生成的导引指令继续控导引弹。

图3 视场角约束示意Fig.3 Concept of Field of View Constraint

4.2 仿真算例

4.2.1 时间和倾角控制

本组算例中，飞行器的期望飞行时间固定为td=30 s，各子算例期望倾角和控制总消耗dt如表1 所示。子算例在导引律中均使用n=1，并与控制总消耗最优结果进行对比，表中k/k'分别表示本文所提出方法和数值计算最优结果。由表可知，各仿真条件中，所提出的导引方法控制总消耗与最优结果仅相差7%以内。弹道、倾角、前置角、加速度曲线分别如图4～7所示。

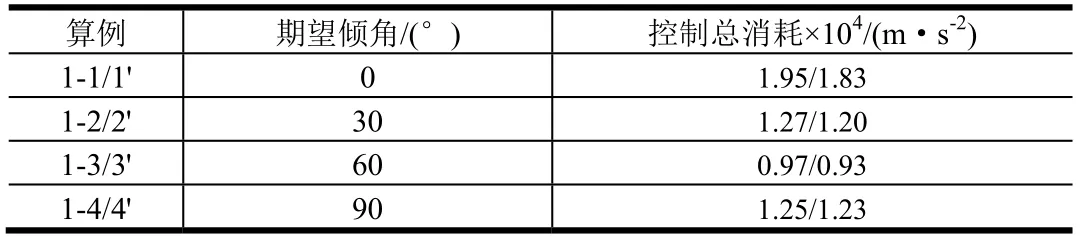
表1 仿真算例1 控制总消耗结果Tab.1 Total Control Effort of Case1

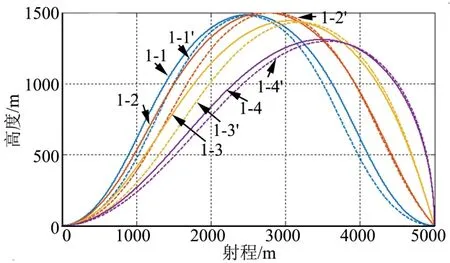
图4 算例1 弹道曲线Fig.4 Trajectory of Case 1

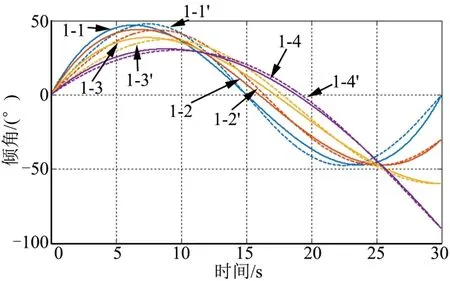
图5 算例1 弹道倾角曲线Fig.5 Flight Path Angle Profile of Case 1

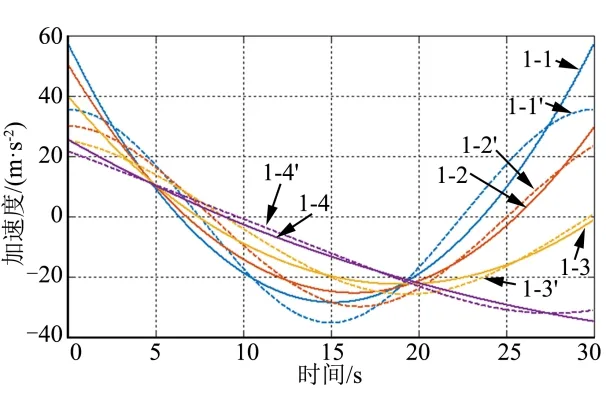
图7 算例1 加速度曲线Fig.7 Acceleration Profile of Case 1

4.2.2 带有视场角约束的时间和倾角控制

本组算例中，期望飞行时间 td=30 s，期望倾角γd= 0。视场角限制设置为 εmax=−εmin=50°，限制区域ρ=2°。飞行器自动驾驶仪延迟时间常数设置为τ =0.2 s。飞行器飞行时间误差和期望倾角误差如表2所示。其中2-1 开启视场角约束式（29），2-2 关闭视场角约束。弹道及视场角曲线分别如图8、图9 所示。由图8 可知，约2 s 时，视场角达到预设值，2-1 将视场角限制在了50°之内，而2-2 超出了视场角限制。由表2 可知，视场角约束方法式（29）对飞行时间和末端倾角的影响较小。

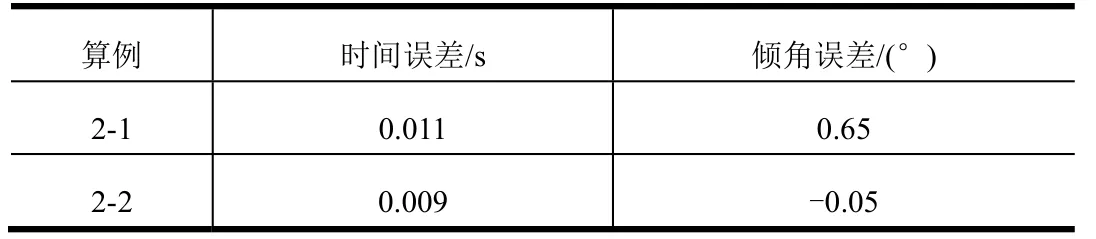
表2 仿真算例2 导引误差结果Tab.2 Summary of Guidance Error

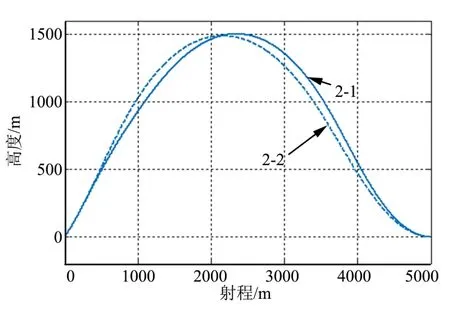
图8 算例2 弹道曲线Fig.8 Trajectory of Case 2

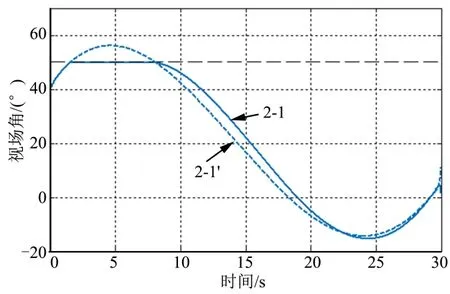
图9 算例2 视场角曲线Fig.9 Look Angle Profile of Case 2

5 结 论

本文采用时间多项式设计前置角变化规律，提出了带有飞行时间和末端弹道角约束的导引律。引入前置角初始条件和命中目标的终端条件，使多项式中待定系数减少至两个，用于控制飞行时间和末端倾角。之后在线性化模型的基础上，引入末端弹道角作为终端约束，建立了两个系数之间的联系，使待定系数减少至1 个。采用在线更新导引系数的方式，根据碰撞几何及弹目相对运动关系的变化不断更新线性化模型，得到了闭环形式导引律。仿真结果表明，所提出的导引律在控制总消耗上十分接近最优结果，能够在视场角受约束情况下，有效实现对飞行时间和末端倾角的控制。