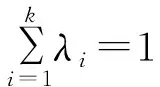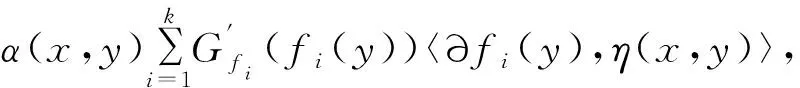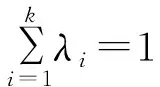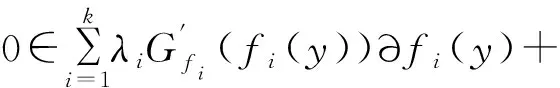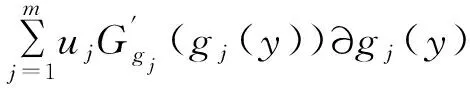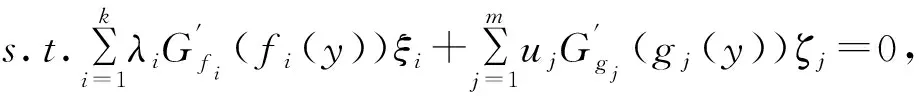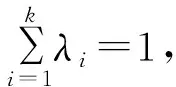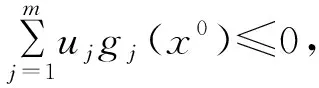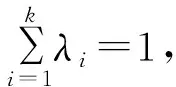(G-V)-不变凸多目标规划的Wolfe型对偶条件
2020-10-12刘靖雯李向有
刘靖雯,李向有,江 柳
(延安大学数学与计算机科学学院,陕西延安716000)
对偶问题是数学规划中很重要的研究内容,一般对偶问题分为Mond-Weir型对偶和Wolfe型对偶。在过去的二三十年里,不同学者利用不同的凸函数研究了大量对偶问题,得到了很多重要的结果。如:孙玉华[1,2]等人研究了B-(p,r)-不变凸函数的Mond-Weir型对偶理论以及Wolfe型对偶理论;赵丽丽[3]讨论了广义(F,α,β,d)-V-凸多目标规划问题的最优性与对偶性;李丽,张庆祥[4]研究了(F,α,β,d)-对称凸性下多目标规划的Mond-Weir型对偶。G不变凸函数是Antczak提出一类新的广义的不变凸函数,随后他利用这类函数研究了可微的G不变凸函数限制下的多目标规划的Mond-Weir型对偶[5-7]。Kang[8]和Kim[9]又将该G不变凸函数推广到非可微情形,研究了非可微多目标规划问题Mond-Weir型对偶,得到了非可微G不变凸性下Mond-Weir型对偶条件。近年来,Antczak[10]定义了非可微(G-V)-不变凸函数,把G不变凸函数推广到向量情形,并用这类函数研究了非可微多目标规划的Mond-Weir型对偶理论。
受上述文献启发,本文将利用(G-V)-不变凸函数研究一类非光滑多目标规划问题,重点研究Wolfe型对偶问题,给出相应的弱对偶、强对偶及严格逆对偶定理。
1 基本定义
称实值函数f:Rn→R是局部Lipschitz的[11],若对任意x∈Rn,存在一个正数k和x的邻域N(x)对任意y,z∈N(x),使得
‖f(y)-f(z)‖≤k‖y-z‖。
若函数f为局部Lipschitz的,那么函数f:X→R在点x处沿方向d的Clarke广义方向导数和Clarke广义梯度分别定义为[11]:
∂f(x)={ξ∈Rn:f0(x;d)≥ξTd,∀d∈Rn}。
下面的不等式在整篇文章中都成立,对于任意x,y∈Rn,
x≦y⟺xi≦yi;x≤y⟺xi≦yi,但x≠y;
x 设x⊂Rn,u∈X,令f=(f1,…,fm):X→Rn,fi(i=1,…m)是定义在X上的局部Lipschitz函数,令Ifi(x),i=1,…,m表示fi的值。T.Antczak在文献[10]中定义了非可微(G,V)不变凸函数,让我们回忆一下。 定义1[5]设函数Gf=(Gf1,…,Gfk):R→Rk,其每个分量Gfi(x):Ifi(x)→R,i=1,…k均是严格单调递增的可微实值函数,函数α:X×X→R+,η:X×X→Rn,若对x∈X,∀ξi∈∂fi(y),y∈X,i=1,…,k,有: Gfi(fi(x))-Gfi(fi(y)) 则称f在y∈X相对于函数α,η是非可微(G-V)-不变凸函数。若在上式中x≠y且换成>,则称函数fi在y∈X相对于函数α,η是非可微严格(G-V)-不变凸函数。 显然:当Gf=(Gf1,…,Gfk):R→Rk,其每个分量Gfi:Ifi(x)→R,i=1,…k均是恒等映射时,f在y∈X相对于函数α,η是(G-V)-不变凸函数。 定义2[5]D为满足规划问题(VP)约束条件的所有点的集合。x*∈D是(VP)的可行解,若找不到x∈D使得f(x)≤f(x*)成立,则称x*为该问题的有效解。 考虑下列多目标规划问题(VP) 这里X为Rn上的非空开集,fi:X→R(i=1,…,k),gj:X→R(j=1,…,m)均为局部Lipschitz的实值函数。记(VP)的可行域为D={x∈X|gj(x)≤0,j=1,2,…,m}。 (VP)的对偶规划定义为(VD): maxGf(f(y))+uTGg(g(y)e)=(Gf1(y))+ uTGg(g(y)),…,Gfk(fk(y))+uTGgg(y)), ujGgj(gj(y))0,j=1,…m, λi≥0,i=1,…,k,uj0,j=1,…,m。 这里fi:Rn→R,(i=1,…,k),gj:Rn→R均为局部Lipschitz的实值函数,Gf=(Gf1,…,Gfk):R→Rk,每个Gfi:Ifi(x)→R,i=1,…k是严格单调递增的可微实值函数,Gg=(Gg1,…,Ggm):R→Rm每个分量Ggj:Igi(x)→R,j=1,2,…,m是严格单调递增的可微实值函数且Gfi(0)=0,Ggj(0)=0,eT=(1,…,1)。 定理1 (弱对偶)若以下条件成立: (i)x,(λ,u,y)分别是(VP)和(VD)的可行解; 则Gf(f(x))Gf(f(y))+uTGg(g(y))e。 证明不妨设 Gf(f(x))Gf(f(y))+uTGg(g(y))e,可得 Gfi(fi(x))Gfi(fi(y))+ 因为ujgj(x)≤0,j=1,…,m,有 又有λi≥0,i=1,…,k,则有 整理得 (1) 由定理条件ii有 Gfi(fi(x))-Gfi(fi(y))> λiGfi(fi(x))-λiGfi(fi(y))> (2) 同理可得 (3) (2)+(3)可得 (4) ∃ξi∈∂fi(y),ξi∈∂gj(y), (5) 故(1)和(5)矛盾,所以Gf(f(x))Gf(f(y))+uTGg(g(y))e,结论成立。 定理2 (弱对偶)令: (i)x,(λ,u,y)分别是(VP)和(VD)的可行解; 则Gf(f(x))≮Gf(f(y))+uTGg(g(y))e。 证明与定理1类似,此处省略。 定理3 (强对偶)设x是(VP)的有效解,假设x满足(G-V)约束条件,(λ,u,y)是(VD)的可行解,若定理1的弱对偶条件成立,则(λ,u,y)是(VD)的有效解。 证明类似于定理1的证明。 定理4 (严格逆对偶)令: (i)x,(λ,u,y)分别是(VP)和(VD)的可行解且有λTGf(f(x))λTGf(f(y))+uTGg(g(y)); 则x=y,且y是(VP)的有效解。 证明先证x=y。现假设x≠y,由定理条件ii得 α(x,y)(Gfi′(fi(y))∂fi(y)+ 由于λi≥0,i=1,…,k,则 α(x,y)(λiGfi′(fi(y))∂fi(y)+ (6) 由于(λ,u,y)是(VD)的可行解,则 ∃ξi∈∂fi(y),ζi∈∂gj(y), (7) 故有 (8) 由G函数是严格单调递增的,有 与条件i矛盾,所以x=y。 再证y是(VP)的有效解。不妨设y不是(VP)的有效解。 由定义2有:∃x0∈D,s.t.f(x0)≤f(x),则 fi(x0)≤fi(x), 因为λi≥0,i=1,…,k, 所以有:λifi(x0)λifi(x), 因此λiGfi(fi(x0))λiGfi(fi(x))。 由定理条件i知 显然有 λiGfi(fi(x0))λiGfi(fi(x)) (9) 定理条件ii有 (10) 即y是(VP)的有效解。2 Wolfe对偶性条件