Smarandache LCM函数与伪Smarandache函数的混合均值

高 倩，高 丽，梁晓艳

(延安大学数学与计算机科学学院，陕西延安716000)

文献[7]研究了伪Smarandache函数与Smarandache LCM函数的混合均值，即对任意实数x≥2,k≥2，有渐近公式

其中αi(i=1，2，…，k)为可计算的常数。

本文基于上述文献，利用初等及解析的方法，证明了如下定理:

定理设k≥2是给定的正整数，则对任意的实数x≥2，有渐近公式

其中di(i=1，2，…，k)为可计算的常数，ζ(n)为Riemann Zeta-函数。

1 相关引理

引理1[8，9]对任意的素数p≥3即k∈N,z(pk)=pk-1。

当p=2时，则有z(2k)=2k+1-1。

若n为任意合数时，

z(n)=max{z(m):m|n}。

引理2[10]对于任意素数p，有sl(pk)=pk。

引理3[11]设实数x≥2，则有

其中ci(i=1，2，…，k)为常数且c1=1。

2 定理的证明

(1)讨论集合A的情况，由引理1和2知：

(2)讨论集合B的情况，由引理1知：

(1)

于是由引理3及Abel求和公式以及分部积分法有：

其中bi(i=1，2，…，k)为可计算的常数。

其中ci(i=1，2，…，k)为可计算的常数。

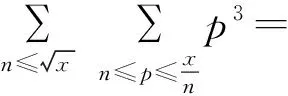
(2)

其中di(i=1，2，…，k)为可计算的常数，ζ(n)为Riemann Zeta-函数。

(3)

其中ei(i=1，2，…，k)为可计算的常数。

结合(1)(2)(3)式有

其中di(i=1，2，…，k)为可计算的常数。

(3)讨论集合C的情况，据z(n)的性质及集合C的定义可知，对于任意的正整数n∈C，当n的标准分解式n=p1α1p2α2…psαs，此时分两种情况：

z(n)=max(z(piαi)}=piαi-1

其中αi≥2，可以判断

综上所述可得

其中di(i=1，2，…，k)为可计算的常数。

于是该定理得证。