一种核空间中改进的KISS行人再识别算法

徐同文，白宗文*，杨延宁

(1.延安大学物理与电子信息学院；2.陕西省能源大数据智能处理省市共建重点实验室，陕西延安716000)

行人再识别[1，2](Person Re-identification,ReID)是指在无重叠视域摄像机网络中，对同一个行人目标进行匹配跟踪。因此，行人再识别在大型场所的安防监控管理上有非常广泛的应用前景。在不同摄像机拍摄的海量视频中，对同一个目标进行人工跟踪管理，不仅耗费大量的时间，而且很有可能造成目标跟踪失败。行人再识别就是在没有人参与的情况下对同一个目标进行跨摄像机跟踪。但是行人的非刚性姿态、不同光照以及背景噪声等条件下摄像机所采集图像的差异性，这都对行人再识别研究提出了严峻的挑战，同时也是当前本领域的热点和难点问题。

深度学习方法是当前人工智能研究热点之一，虽然深度学习在行人再识别中取得了较高的识别精度，但是其模型需要大量的训练和测试样本，而且学习出的模型泛化能力也有一定限制。如何学习出一个有效的度量矩阵，也是当前研究者的一个重要热点。KISS算法是由Kostinger等人[3]提出的基于贝叶斯概率正负样本对的度量算法。由于算法步骤简单、学习出的马氏距离度量矩阵有效而且算法精度较高，因此KISS算法是当前行人再识别中常用的经典算法之一。宋丽丽等人[4]认为KISS算法的模型参数估计容易出现过拟合现象，因而提出对样本进行重采样，增强模型的泛化能力，提高KISS算法的精度，但是重采样过程有些复杂。Liao等人[5]认为使用PCA对特征向量降维影响了KISS算法中的半正定矩阵的学习，因此提出了把降维嵌入到度量矩阵的学习中去，在学习半正定矩阵的同时学习出一个降维矩阵，结果表明改进后的算法精度优于KISS算法。Tao等人[6]认为KISS算法过高的估计了半正定矩阵的特征值，因此提出DR-KISS对特征值进行正则化。齐美彬等人[7]认为，在核空间中使用KISS算法，可以有效的解决特征向量数据的非线性，实验结果表明把特征向量映射到核空间中，再使用KISS算法可以大大增加了算法的精度，取得了很好的效果。

但是在核空间中，KISS算法只用了两个向量的差来学习半正定矩阵，并没有把向量的有效信息全部包含进来，两个向量的和[8]同样也可以表示两个向量的相似性，因此本文在学习KISS算法的半正定矩阵时把两个向量的和信息也加入进来，实验结果表明使用两个向量的和向量和差向量学习出的半正定矩阵包含更多的信息，可以有效的用来计算两个向量的相似度，提高KISS算法精度。

1 核空间中改进的KISS算法

1.1 基于核空间的KISS算法

kKISS算法是文献[7]提出的，它首先把行人的特征向量使用核函数从低维空间映射到高维空间，以此增加向量的线性可分性，然后在核空间中使用KISS算法进行向量间的相似度度量。

1.1.1 核空间映射

假设vi是原始空间里面的一个特征向量，使用核函数φ映射到核空间即高维空间中，得到高维空间中的特征表达ki。使用核函数得到高维空间的特征表达式为

ki=[φ(v1,vi)],φ(v2,vi)，…φ(vn,vi)]，

其中v1，v2，…vn是低维空间里面的n个样本向量。核函数φ为RBF卡方指数核函数。

1.1.2 KISS算法

Kostinger等人[3]为引出马氏距离中度量矩阵的学习方式，从统计学的角度提出了KISS算法。

假设xi和xj分别代表描述行人的两个特征向量，两个向量的差值表示为xij=xi-xj。HI表示两个特征向量是相似的，HE表示这两个特征向量不相似，则KISS算法定义描述两个向量的相似度值用出现这两种情况下的概率值的比值对数来表示：

(1)

从公式看出，如果δ(xi,xj)的值越大，就说明HI出现的情况可能性越大也就是这两个特征向量越相似，反过来，如果δ(xi,xj)的值越小，就说明HE出现的情况可能性越大这两个向量越不相似。算法假设xij符合高斯分布，那么δ(xi,xj)可以重写为：

(2)

忽略上述公式的常数项，可以得到：

(3)

(4)

(5)

NI和NE分别为情况HI和HE下训练集样本数量。

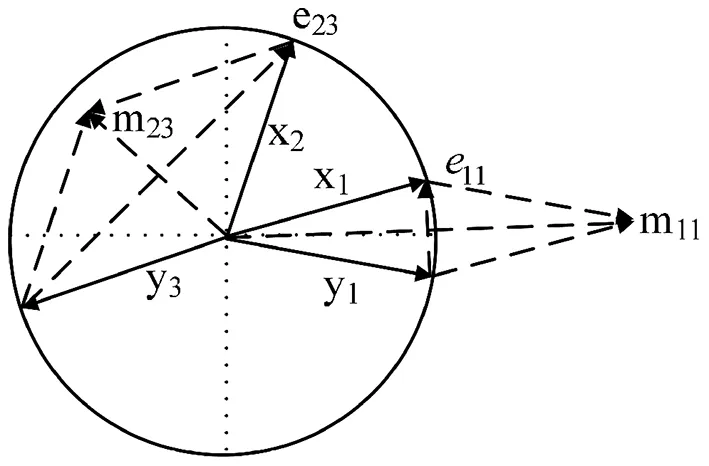
图1 两维空间中向量示意图

1.2 改进的kKISS算法

对于一个图像对(xi,yi)，xi,yi分别表示描述行人的特征向量。LSSL算法[8]定义：两个向量的差为e=x-y，向量的和为m=x+y。如图1所示，图像对(x1,y1)是一对相似的向量，(x2,y3)是一对非相似的向量。从图上发现，相似对(x1,y1)的差值模‖e11‖很小，而和值模‖m11‖大。同时，非相似对(x2,y3)的差值模‖e23‖大，而和值模‖m23‖小。因此，如果把两个向量的和也用来表示这两个向量的相似性，这样可以得到更多的信息。

LSSL算法定义两个向量的相似性度量值为：r(x,y)=mTAm-λeTBe，其中A、B为两个向量的和向量和差向量的协方差矩阵，λ是常数。

根据KISS算法，可以得出

对于一个相似对(xi,yi)，i=1，2，…，N，有xi=ui+εil和yi=ui+εi2，其中ui表示行人真实的特征向量表示，εi1、εi2分别表示为对摄像机拍摄到图像提取特征向量对真实的特征向量的偏差。

于是有eii=εi1-εi2，mii=2ui+εi1+εi2。

因为ui,εi1,εi2是分布是独立的。因此可以得出

cov(e,e)=2Sε，cov(m,m)=4Su+2Sε，因此有

P(m|Hs)=N(0,∑mS)，P(e|Hs)=N(0,∑eS)，

其中∑mS=4Su+2Sε，∑eS=2Sε。

对于非相似对(xi,yi)，i≠j，i,j=1，2，…，N，xi=ui+εi1和yj=uj+εj2，得出

eij=ui-uj+εi1-εj2，mij=ui+uj+εi1+εj2，

其中ui,uj,εi1,εi2是独立分布的，因此得出

cov(e,e)=2Su+2Sε，cov(m,m)=2Su+2Sε。

因此，P(m|HD)=N(0,∑mD)，

P(e|HD)=N(0,∑eD)，

其中∑mD=2Su+2Sε，∑eD=2Su+2Sε，

观察以上两式和相似对的和向量和差向量的协方差矩阵

∑mS=4Su+2Sε，∑eS=2Sε，可以得出

EmD+EeD=EmS+EeS和EmD=EeD，

令∑=(∑mS+∑eS)/2=∑mD=∑eD，

因此KISS算法中的M矩阵可以重写为

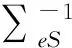
从上面的公式讨论可以看出，半正定矩阵M可以由向量对的和向量和差向量联合学习出，这比KISS算法中单独使用两个向量的差向量学习出包含的信息更多，因此联合学习出的M矩阵用于计算向量的相似度时更精确。

1.3 特征表达

在进行向量间的相似性度量之前，需要把图像进行特征描述，使行人图像转换成向量的形式。本文使用RGS、YCbCr、HSI、HSV四种颜色特征进行行人的特征表达，首先把图像水平6等分，在每一个等分条带中每一个颜色通道提取16 bin的颜色直方图。一种颜色空间有三个通道，因此提取出的特征向量维数为16×6×3=288维。另外，本文还使用HOG特征进行行人的外观形状描述，把颜色特征和HOG特征串联融合起来就得到了行人最终的特征表达[7]。

2 实验结果与分析

2.1 公共测试集与算法评价标准

本文实验在Intel(R)CoreTM i5-7500 CPU，频率3.40 GHz，内存4.00 Gbyte Matlab 2014a基础配置环境下进行。

VIPeR数据集是行人再识别算法测试中最常用的公共数据集之一。它是由两个摄像机拍摄到632个行人共1264张图像组成的。每一个行人的图像像素为128×48。在算法测试中，随机抽选316个行人即632张图像做训练集，剩下的632张图像做测试集。CUHK01也是由两个摄像机采集到图像组成的。一共有971个行人，每一个行人图像的像素为160×60。在测试中，随机选取485个行人的图像做训练集，剩下的486个行人的图像做测试集。

本文采用累积匹配特性(CMC)曲线[3]作为评价量化算法精度的标准。

2.2 仿真实验结果与分析

本文提出的方法与当前的一些算法在两个公共测试集上VIPeR和CUHK01的结果对比如下。如图2所示，在VIPeR数据集上本文算法和五种算法(kKISS、SCNCD、LMNN、ITML、KISSME)的CMC曲线图，从图中可以看出，本文提出的方法rank1的精度为37.03%，高于其他算法，并且本文算法精度从rank1到rank15的精度一直比其他算法高。为进一步比较实验结果，如表1所示，列出本文在rank 1、rank 5、rank 10、rank 15、rank 20上与其他算法的精度对比，从表中可以看出，本文的方法在rank1这个重要指标上比kKISS算法高出3.04%，这说明，在学习半正定矩阵时，充分运用到了两个向量的和来补充表征两个向量的相似度可以得到更多的向量信息，学习出的半正定矩阵更具有可识别性。

图2 本文算法与当前算法在VIPeR上的比较。rank 1精度标记在算法名称前。

同样如表2所示，为本文提出的算法与其它算法在CUHK01数据集上的精度对比。从表中看出，本文的算法精度在rank 1至rank 20上达到了最优的识别精度，在rank 1精度上比kKISS算法提高了2.47%。这样同样验证了本文提出的半正定矩阵比kKISS算法学习出的矩阵富含更多的信息，更具有有效性。

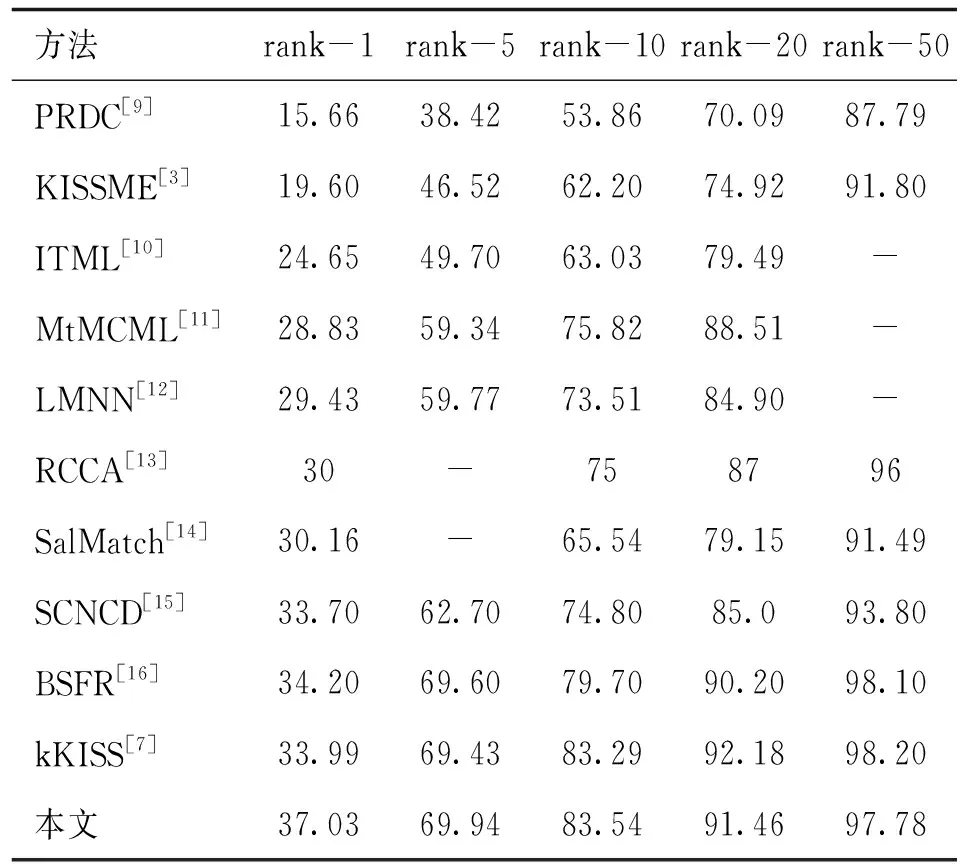
表1 本文算法与当前算法在VIPeR上的识别精确比较(%)

表2 本文算法与当前算法在CUHK01上的识别精度比较(%)

3 结论

本文提出了基于核空间中改进的KISS行人再识别算法。针对KISS算法计算半正定矩阵只用到两个向量的差向量而包含信息有限的问题，提出在学习半定矩阵时同时使用向量的差向量和和向量，这样学习出的矩阵包含的信息更多，计算出的相似度更精确，两个数据集上的实验结果表明本文所提出的算法精度超过了多种常用算法的精度，并且rank1精度优于kKISS，验证了本文算法的有效性。