基于排队论M/M/C模型的门诊医技排程与医疗设备配置的统筹优化研究
2020-10-12刘伟军邹泽邱宾王凤张恩科
刘伟军,邹泽,邱宾,王凤,张恩科
陕西省人民医院 a. 医学装备部;b. 核磁室;c. 信息处;d. 耗材试剂部,陕西 西安 710068
引言
随着国家医疗改革的不断深入以及进一步改善医疗服务行动计划[1]的不断落实,医疗机构也不断通过创新管理手段、加强精细化管理和提高内涵建设等举措,促进医疗服务水平不断提高[2]以及患者就医体验不断改善。门诊医技诊疗检查作为医疗工作中的一个重要组成部分,其合理的医技排程和科学的设备配置已是医疗机构管理的重要内容之一[3],两者科学精准的统筹优化研究对门诊医技诊疗服务管理和医疗设备配置管理具有非常重要的作用和意义[4]。本文以我院MR 诊疗服务为例,研究医技排程与设备配置的统筹优化方案。
1 数据来源与研究方法
1.1 数据来源
数据统计资料为我院MR 在2019 年1 月至2019 年12 月期间患者诊疗检查项目的例数(并非诊疗检查人次的次数),均统计于我院HIS。
1.2 研究方法
基于数据统计资料,应用排队论M/M/C 模型对MR 服务系统进行分析,借助软件工具计算相应的参数数值,以此建立MR 医技排程与设备配置的量化关系[5],统筹研究两者的优化方案。
1.2.1 排队论M/M/C模型
排队论是解决排队控制问题的数学理论和方法,对一个客观复杂的排队结构进行科学准确的分析,属于运筹学的一部分[6]。
排队系统由三个基本部分组成,包括:输入过程、排队规则和服务单元[7],见图1。我院MR 检查项目排队模型的选择依据三个基本部分的属性而决定:① 输入过程:由于患者的到来是无限性的、随机性的并且独立性的,因此检查项目的输入属于最简流(Poisson 流),服从负指数分布;② 排队规则:患者检查项目的排队规则属于等待制,服务顺序为先到先服务;③ 服务单元:服务单元即MR,其设备数量C≥1 台。由于核磁检查项目固定,其服务时间相对稳定,故服务时间分布近似服从负指数分布。由以上三个基本部分的属性决定了模型选择为:M/M/C 模型[8-10]。
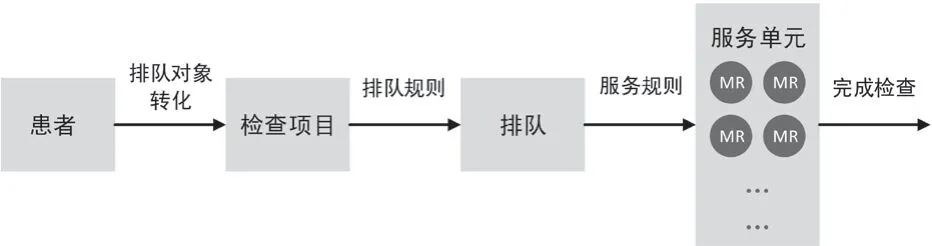
图1 MR服务排队系统模型图
1.2.2 数据处理
M/M/C 模型的参数数量较多且计算也较为复杂,一般有两种简便的计算方法:其一,运用MATLAB(矩阵实验室)进行编程仿真计算[11];其二,运用Microsoft Office Excel(个人计算机数据处理软件)加载Queuing Toolpak(流程管理软件工具包)进行数据分析计算[12]。
Queuing Toolpak 由一个函数库组成,可以作为Excel的插件执行排队模型的分析计算,并且将排队性能度量集成到电子表格中[13]。相较于MATLAB 编程仿真计算,其计算过程更为简化,结果更为直观。本文借助Microsoft Office Excel(版本:Professional 2007)加载Queuing Toolpak(版本:4.0)作为排队模型参数的计算工具。
2 模型应用
2.1 模型构建
M/M/C 模型由12 个参数构成,其中C、λ和μ为模型的基本参数[14-16],相关参数表达和含义如表1 所示。模型的数学算法如式(1)~(2):



表1 M/M/C 模型参数的表达和含义
2.2 模型计算
(1)λ的计算。定义医技排程载量定义为一年服务天数与一天服务时间的乘积,即P=D · T。λ是排队系统服务规则的体现,与医技排程载量有直接关系[17],即:其中,Z表示系统服务载量,即年检查项目数量,单位为个;P表示排程载量,是服务规则的数学语言描述,单位为h;D表示一年服务天数,单位为天;T表示一天服务时间,单位为h。
(2)μ的计算。μ是排队系统服务能力的体现,与设备配置的数量有直接关系[18]。我院有4 台MR,每台MR 品牌和规格不同以致扫描性能存在差异,并且不同扫描项目用时不一,为了能精确计算该MR 服务系统的平均服务率,在已知每个项目的平均用时的条件下,借助HIS 统计了2019 年MR 全年的检查项目及其年检查数量,见表2,可以精确计算单个检查项目的平均用时,可得μ=1/0.18=5.47 个/h。
(3)计算结果。我院目前共有4 台MR,应对服务载量为115293 个项目检查,不得不超负荷运作,为此MR 全年无休最大限度的服务,除去故障停机和运维保养所用天数,每台MR 平均每年服务357 天,并且每天服务时间超过8 h,即D≤357 天,T≥8 h。运行Queuing Toolpak,将C、λ和μ三个基本参数数值导入,可得ρ、Lq、Ls、Wq、Ws和P各参数数值,其中P=D · T,D取最大数值357 天,T取对应范围内最小整数的数值(8≤T≤15 h),计算结果如表3所示。

表2 2019 年MR 检查项目的年检查数量及其用时情况

表3 MR 排队系统不同排程载量和设备配置下的各参数数值
2.3 结果分析
(1)相同排程载量下设备配置与各排队参数的关系。从表4 将排程载量相同而配置数量不同的参数数值摘录出来,可明显看出配置数量的多少直接影响排队参数的高低,设备数量C越大,则ρ的数值越小,说明了排队系统的整体服务强度越高;当设备数量C达到一定数量时,则会出现Lq≤C,可以理解为检查项目数量少于排队需求,该系统不需要排队,符合该条件参数的排队系统是理想型[19]。
(3)我院目前MR 服务排队系统运作情况。我院MR设备数量C=4 台时,在一年服务天数D=357 天,并且一天服务时间T=15 时的条件成立下,排队系统的服务强度ρ<100%,即该系统可以完成服务载量为115293 个项目检查,其中平均排队检查项目的数量Lq为45.79 个,系统中平均逗留的检查项目的数量Ls为49.73 个,检查项目从到达到接受服务的平均等待时间Wq为2.13 h,检查项目从到达到完成服务的平均时间Ws为2.31 h。
总体来说,每个项目检查等待时间可以接受,但排程载量较满,医护工作时间超出额定时间近一倍,五分之一的检查项目要在晚上八点至十一点完成(早上八点准时开始检查服务),包括国家法定节假日和公休日,该时间段患者就医体验不佳,医护工作强度较大。
(4)理想状态下我院门诊医技排程与医疗设备配置优化方案。理想状态是指一年服务天数为251 d,一天工作时间为8 h,排队系统无需排队,即Lq<C[20]。通过模型计算可得设备数量C为12 台,服务强度ρ为0.87%,平均排队检查项目的数量Lq为3.45 个。
达到理想状态下的检查排队系统,需要添置8 台MR。出于场地和资金的考虑,该理想型方案实现确实困难。
(5)条件限制下我院门诊医技排程与医疗设备配置优化方案。评估了我院场地和资金情况,可增加2 台MR,即C=6 台。为了提升医技诊疗服务水平,确保患者就医的最佳体验,即Lq≤C=6 个。通过模型计算可得排程载量P=D·T=3 965.86 h,该等式可看作是两个变量的反比例函数。通过综合考虑,设定D=331 天,则T=11.98≈12 h。与增配优化前相比,见表4,增配优化后的一年服务天数降低26 天,即每周每台MR 停机休息可多出了0.5 天,一天服务时间降低了3 h,晚上八点就可停机休息,检查项目从到达到接受服务的平均等待时间缩减了1.93 h,由此患者就医体验和医护工作强度都得到了明显的改善。

表4 条件限制下增配优化前后的排队系统参数数值
3 讨论
本文依据排队系统各参数的相关性,构建M/M/C 模型统筹优化门诊医技排程与医疗设备配置。相较传统的经验法和简单的数学算法,该方法不仅能够充分体现各参数数值的变化信息,而且能够便捷的将数个因素做为变量纳入模型转换成简单函数进行分析[21]。该方法的运用将医技排程与设备配置优化方案变得函数化和数量化,其方案更为精准和直观,有助于医疗机构统筹医技排程管理、优化装备配置决策,进而提升医疗诊疗服务。该方法的应用还需注意以下两点:其一,一定要准确计算平均到达率λ和平均服务率μ,其结果直接影响该系统的精确度;其二,本文是在应对服务载量(即年项目检查数量)不变以及服务规则为等待制的基础上进行的研究,如果将应对服务载量的趋势变动和极小部分的患者流失这两个因素纳入考虑,服务流程更加符合实际、计算方法将更加完善、方案结果将更加科学。
