基于四元数的医用机器人定位准确度评价

2020-10-12王浩孟祥峰王权张超王晨希李佳戈

中国医疗设备 2020年9期

王浩，孟祥峰，王权，张超，王晨希，李佳戈

中国食品药品检定研究院光机电室，北京 100050

引言

近年来，在人工智能、自动控制与传感器技术的推动下，医用机器人领域发展很快，面向骨科、神经外科、心血管等临床需求，科研成果不断涌现[1-5]，国产创新产品也在陆续上市[6]。根据国外医用机器人应用情况和监管机构的反馈[7]，医用机器人的安全性、有效性研究还有待深入，临床风险依然存在，产品质量评价、上市前、上市后监管缺乏专用的标准体系，急需研究和完善。从标准化的角度看，国际电工联合会、国际标准化组织等都在积极推进标准化研究。在电气安全方面，康复机器人[8]、手术机器人[9]等国际标准已经发布，从医用电气设备的电气安全角度指导质量评价。在风险管理方面，医疗器械自治能力[10]国际标准也已经发布，提出了自治能力分级的理念，有助于开展医用机器人的风险管理活动。

在性能方面，医用机器人缺乏专用标准，关键指标与评价方法尚未建立，部分沿用工业机器人的评价思路[11]，对医疗器械的特殊性考量有待加强[12-13]，方法也需要完善。其中，定位准确度是描述机械臂精准操作器械能力的重要指标之一，目前业内缺乏统一的评价方法，影响产品检验结果的可比性与可溯源性，阻碍产品上市与后续监管。根据数学原理，如何建立机器人坐标系（产品）与测量工具（检验设备）坐标系之间的转换关系，是评价医用机器人定位准确度的核心问题，不同的机器人标准给出的方法差别较大，例如GB/T 12642-2013[11]使用立方体或长方体作为体模，选择对角面上的五个点为靶点计算定位准确度，而ASTM F2554-2010[14]使用特殊形状的凹槽体模（预先标记47 个点），选取至少6 个靶点计算定位准确度。上述标准均未描述具体的坐标系转换方法。

本文在实验室条件下使用具体产品和坐标系测量装置进行实验，使用四元数法[15]对坐标系转换结果进行计算，分析坐标系转换模型参数、靶点数量等因素对定位准确度的影响，目的是进一步明确医用机器人定位准确度的测量方法，为下一步建立专用标准提供参考。

1 实验材料与方法

1.1 实验材料与实验环境

待测样品为外科导航式手术辅助机器人，机械臂有6 个自由度，可在边长为1 m 的立方体区域内活动，用于手术器械的固定及方向导引。样品自身的软件组件可以实时记录机械臂器械末端的位置，提供机器人坐标系的读数。该样品声称的定位准确度＜1 mm。实验室测量设备为便携式三维测量臂，可进行接触式位置测量，验收标准满足ISO 10360-12:2016[16]标准，定位测量精度＜0.06 mm，测量范围能够充分覆盖待测样品的活动空间。实验室环境为室内平地，温度为22 室，相对湿度为36%，实验期间保持稳定。待测设备和测量臂底座固定，未见明显振动或位移。

1.2 坐标系转换模型

机器人机械臂器械末端坐标系记为坐标系r，实验室设备的测量工具头坐标系记为坐标系l。实验室设备和机器人分别记录靶点坐标，记为rl和rr。实验室设备的点坐标rl转换到机器人坐标系下，得到预测点，那么预测点与机器人实测点rr之间的距离即定位准确度。

根据四元数法的思路，坐标系转换可分解为三个步骤，即“平移—拉伸—旋转”。假设靶点位置在机器人与测量臂测量时均保持不变，即轨迹内部各点的相对位置不变（符合刚体定义），且两个坐标系都是直角坐标系，数学模型可以用公式(1)表示：

其中r0代表平移量，s代表比例因子（拉伸或压缩的倍数），R为旋转函数或旋转矩阵。平移量实质上是两个坐标系原点的距离。在坐标系转换过程中，坐标系r和坐标系l 可以分别减去全体靶点的几何中心坐标，使得两个坐标系的原点重合，此时平移量为0，记平移后的坐标值分别为rl'、rr'。对刚性物体而言，比例因子理论上等于1，那么公式(1)变成了对旋转矩阵的直接求解。利用坐标系转换中的点积不变性，使用三组通过机器人坐标系rl原点的三个彼此正交的单位向量和工具坐标系l 对应的向量，分别与同一个靶点对应的向量求点积，可重建旋转矩阵。

在实际测量与计算中，比例因子和旋转矩阵的求解属于优化问题，等同于寻找使预测点与实测点之间误差最小的匹配关系。本次实验中，总体误差的表述如公式(2)所示，那么优化问题即求解erms的最小值。

其中N为靶点个数，ri,r'、ri,l'分别为第i个靶点在平移后的机器人坐标系和工具坐标系下的值。为了使(2)达到最小值，参考江刚武等[15]的推导，比例因子与旋转矩阵之间可构造如下关系，如公式(3)所示。

当旋转矩阵确定之后，比例因子可通过公式(3)计算得到。

旋转矩阵可以用单位四元数的形式表述。记四元数用于描述旋转关系，其实部和虚部如公式(4)所示。

那么经过推导，旋转矩阵可以表述为公式(5)。

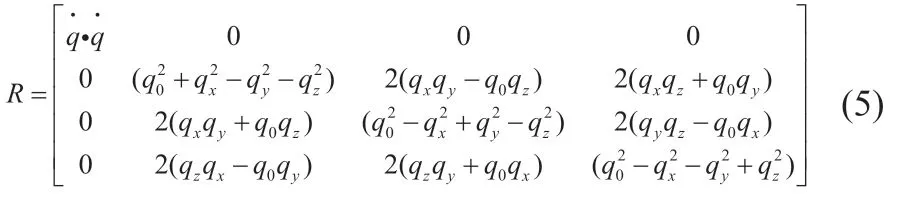
此时优化问题的关键是求解四元数本身。如果把四元数代入(2)，经过系列推导，最终得到是矩阵N 的最大特征值对应的特征向量，N 表述为公式(6)。

其中Sxx可表述为公式(7)，其他可以此类推。以上公式是坐标系转换的依据。

1.3 操作流程

根据实际临床应用，在有效工作空间范围内选取40 个不同位置的靶点。在每个靶点位置，机器人坐标系和工具坐标系（接触式测量）同步记录坐标值。依托40 个靶点，进行坐标系转换计算和定位准确度测量。为了分析靶点数量对定位准确度的影响，从40 个靶点中均匀随机抽样n个点（n从5 到40 递增，步长为5），进行坐标系转换和定位准确度测量，重复500 次，对抽样批和全体靶点分别统计定位准确度的分布情况。

2 实验结果

2.1 总体误差

40 个靶点在机器人坐标系和实验室工具坐标系下记录的原始坐标数值如图1 所示，其中蓝色为实验室工具坐标系记录的坐标值，红色为机器人坐标系记录的坐标值。

使用1.2 中的各公式进行坐标系转换，得到比例因子为0.999 7。图2 所示为各点的定位准确度，最大值1.10 mm，最小值0.10 mm。根据公式(2)计算，得到总体误差为0.59 mm。

可以看出，实际计算得到的比例因子与1 非常接近，刚体假设近似成立。为了进一步评估比例因子对坐标系转换模型的影响，把比例因子替换为1，重新进行计算，得到各点的定位准确度。图3 所示为结果的对比，红色圆圈为比例因子0.999 7 对应结果，蓝色倒三角为比例因子1 对应结果，可见分布趋势相似，但数值变化比较明显。总体误差由0.59 mm 变为0.54 mm，幅度为7.74%。

图1 靶点的原始坐标数值

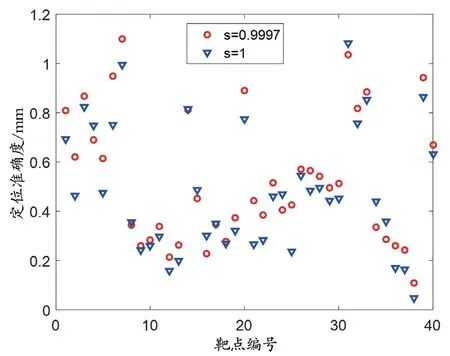
图2 各点的定位准确度

图3 根据不同比例因子计算的定位准确度

2.2 靶点抽样

从40 个靶点中随机抽取的n个靶点（n从5 逐步增加到40，步长为5，每一步抽样500 次）进行坐标系转换，抽样批的总体误差分布与抽样批样品数量的关系如图4 的箱式图[17]所示，红色横线代表每个样本量对应的总体误差中位数，蓝色矩形的上下限代表两个四分限，黑色横线分别代表非异常范围的上下限，红色+号代表极端异常值。根据图4，抽样数量越小，方差越大，极端异常值也越多，说明抽样数量对坐标系转换模型和总体误差都有显著影响。

图4 抽样批的总体误差箱式图

为了进一步观察抽样数量对坐标系转换模型的影响，基于抽样批构建坐标系转换模型后计算全部40 个靶点的总体误差，绘制箱式图，结果如图5 所示。其趋势与图4 相似，抽样点数越多，方差越小，表明实验的精密度越高。

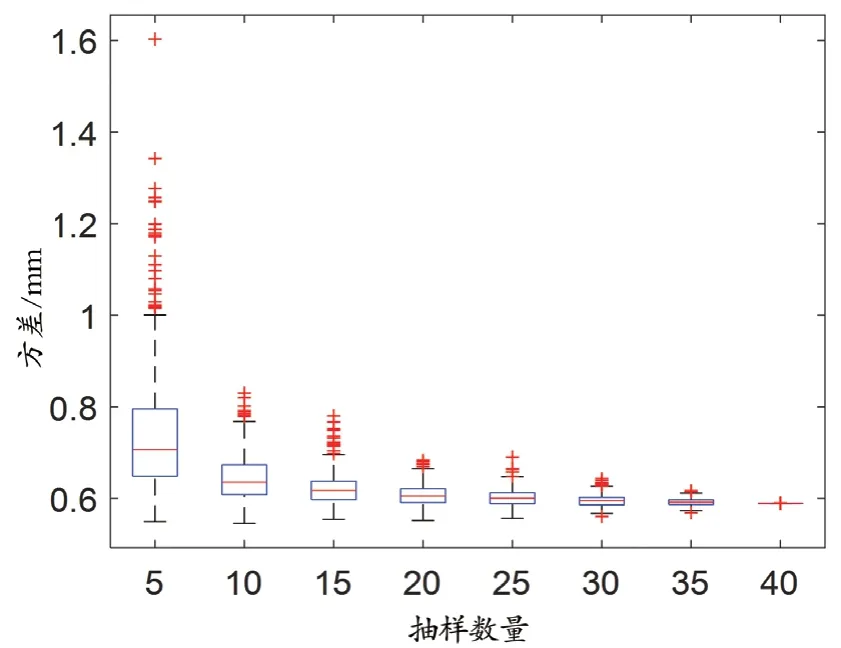
图5 全部靶点的总体误差箱式图

3 讨论

本次实验对医用机器人样品进行了坐标测量，采用四元数模型开展了坐标系转换计算，比较了不同因素对定位准确度结果的影响，发现以下问题在医用机器人的质量评价中需要引起关注。

3.1 四元数模型参数

本次实验中，气候与机械环境平稳，实验室测量设备自身的精度小于待测样品10 倍以上（测量臂精度<0.02 mm，待测样品声称精度<1 mm），测试条件总体良好。在此情形下，比例因子s 的实测值为0.999 7，与刚体的理论值1非常接近，但这两种取值对应计算得到的定位准确度结果却有明显差别（0.05 mm，7.74%）。这说明坐标系转换模型对比例因子的数值比较敏感，或者说梯度较大，意味着对实验条件的要求比较严格，应避免引入额外的机械扰动、环境变化、坐标测量误差等干扰因素。从标准化的角度看，这些因素在医用机器人的定位准确度测量标准中需要予以明确规定，帮助保障不同的检验实验室满足测量结果的一致性和可靠性。

3.2 抽样数量

为评估靶点数量对坐标系转换模型的影响，本次实验选取了不同的抽样数量，分析了抽样批的总体误差和全体靶点的总体误差，结果均说明抽样数量越大，测量结果方差越小，精密度越好。本次实验总共设置了40 个靶点，当采样点数多于30 时，图4 的箱式图非异常范围的上下限之差可收敛到0.2 mm 以下，而图5 的箱式图非异常范围的上下限之差可收敛到0.1 mm 以下，说明用于建立坐标系转换模型的靶点数量、用于验证定位准确度的靶点数量均应设置合理的下限值。由于医用机器人在临床使用中的运动轨迹往往不规则且充满变化，相对工业机器人而言更加复杂，意味着现有工业机器人标准的靶点抽样数量（5 或6）可能难以满足医用机器人定位准确度评价的需要。医用机器人的定位准确度评价有必要结合临床使用场景，在以后的测试和研究中深入展开，加强与其他机器人标准的比较。。

本次实验设计还存在一些不足之处。靶点选取范围基本覆盖了样品的活动范围，但靶点的抽样仅采用了随机抽取的方式，未对靶点组成的空间形状提出进一步的设计，还不能支持体模的研制。下一步的研究有必要对靶点的选取方法开展更深入的评估，包括数量、空间形状要求和距离，使得定位准确度的评价方法更加科学严谨，更接近标准化的需求。