多变量预测控制结构分解的图论方法
2020-10-12王洪瑞王美聪陆云松
王洪瑞 ,邹 涛,张 鑫,王美聪,陆云松
(1.中国科学院沈阳自动化研究所,辽宁沈阳 110016;2.中国科学院机器人与智能制造创新研究院,辽宁沈阳 110016;3.中国科学院大学,北京 100049;4.广州大学机械与电气工程学院,广东广州 510006;5.沈阳化工大学环境与安全工程学院,辽宁沈阳 110142)
1 引言
分层递阶结构广泛应用于大型流程工业过程[1],其中先进过程控制(advanced process control,APC)层的主要功能是基于模型预测控制(model predictive control,MPC)算法实现复杂工业过程的动态实时优化,因此也可以将APC层称为监督控制层(supervisor control)[2].图1中潜在效益最高的是实时优化层,但是实时优化层的成功投运需要APC层的支撑.模型预测控制算法因其能够表征PID控制欠缺的过程动态信息,较好地处理有约束多变量控制问题而被广泛应用在APC层[3–7].与常规MPC相比双层结构预测控制增加了稳态优化层,稳态优化层的出现使APC具有实时动态决策功能[8–10].邹涛提出基于优先级的可行性判定和软约束调整策略综合经济自优化和目标跟踪的稳态目标计算层[11],又给出积分过程优化控制的双层结构预测控制[12],另外在双层结构预测控制下对工业大系统进行集中优化与分散控制[13].
实际应用中系统具有多变量、高维度、目标多样性等特点[14],而双层结构预测控制的计算复杂度主要由变量个数和控制时域决定[15],因此导致其求解复杂、计算量大的难题.受大系统理论启发[16],本文基于图论提出一种多变量系统分解方式,旨在将多变量系统更快速便捷的分解成若干规模较小的子系统,降低求解变量维度,减少计算量.本文首先概述双层结构预测控制及图论,然后采用图论中的邻接矩阵、可达矩阵和关联矩阵对多变量系统进行分解并阐释分解方法,最后通过仿真验证.
2 双层结构预测控制及其优化计算分析
2.1 稳态目标计算层
双层结构预测控制的上层为稳态目标计算层[11,17],可分为经济自优化和目标跟踪两种模式.当过程最优目标受扰动等影响不具有实时性时,稳态目标计算层能够实时决策、动态修改目标设定点,更准确的跟踪实时优化(real time optimization,RTO)层传递的最优操作目标.针对稳态目标求解不可行的问题,基于优先级方法的可行性判定和软约束调整策略能够同时判定优化问题是否可行并求出松弛变量值,根据约束条件重要性定义优先级,并按照优先级的逻辑顺序依次放松约束边界,使稳态目标计算层的实际应用更有价值.
稳态目标计算层经济自优化模式可用LP问题描述,自优化问题又分为最小移动问题和积分变量问题,详情参考文[11].∆uss和∆yss为输入和输出稳态增量,uss和yss为稳态输入和输出,Gu和Gf为输入和扰动的稳态增益矩阵,∆fss为扰动增量,h为代价系数,umax和umin为输入上界和下界,ymax和ymin为输出上界和下界.

目标跟踪模式描述为QP问题,R和Q分别为控制和误差权矩阵,umax和umin为期望输入上界和下界,ymax和ymin为期望输出上界和下界.
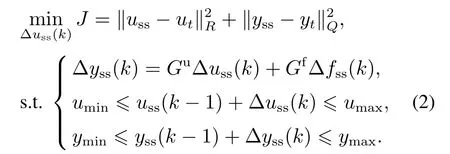
2.2 动态优化层
由稳态目标计算层求出操作变量和被控变量的稳态值,作为动态优化层的设定目标值,进而在线优化求解得到最优控制律.通常把一个多变量有约束的在线优化问题用QP问题描述,A为动态矩阵,∆uM为最优控制增量,w(k)为期望输出,为初始预测值,I为单位矩阵,∆umax和∆umin为控制输入增量上界和下界,M为增量变化个数,m为控制输入个数,B0是M ×M的下三角矩阵.

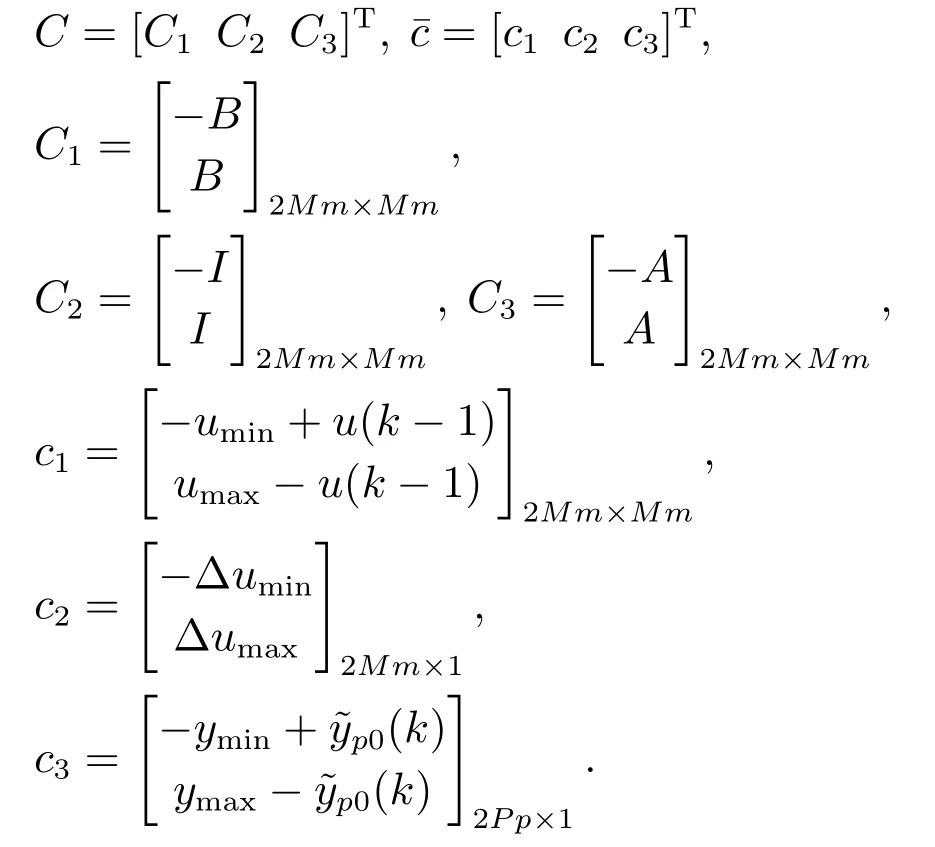
2.3 双层结构MPC中的计算复杂度
双层结构MPC中稳态目标计算层和动态优化层都存在计算量过大的问题,特别是多变量有约束系统,因此为降低计算复杂度,对多变量系统采用分散控制方式减少计算量.在文[15]中对无约束DMC算法计算复杂度分析,提出其计算复杂度主要取决于控制时域M和变量个数m,求解复杂度为O(mM)3.若将系统分解成n 个子系统采用分散控制方式,可知m,根据多项式的立方展开公式分析一定有,故分散控制的计算复杂度必定小于集中控制的复杂度.对于双层结构MPC中有约束的优化问题通常描述成LP或QP问题,LP 的求解方法有单纯形法、原始对偶法等,QP的求解方法有内点法、有效集法等,因此其计算复杂度视其使用的求解方法而定,但是通过分解多变量系统减小计算量的方法同样适用于有约束的优化问题.
3 图论概述
图论是一门研究事物之间联系的学科[18–19],它能够描述事物之间关系,在连续和离散系统、集总和分散系统等的数学建模和分析中都有较重要的作用.
3.1 邻接矩阵
设有向图G=
3.2 可达矩阵
设有向图G=
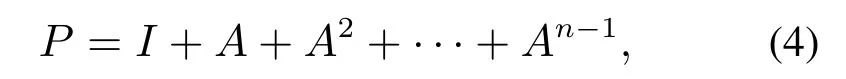
为优化可达矩阵的计算减少计算量,可用(A+I)n−1代替式(4)[21]:

3.3 关联矩阵
在图中将一条边与其连接的两个顶点称做相关联[21–22].设简单无向图G=
3.4 关联矩阵和邻接矩阵快速转换
由定义可知,邻接矩阵描述顶点间的关系,关联矩阵描述顶点与边的关联性,因此对于同一张图二者可相互转换.由关联矩阵以边为媒介得到顶点之间关系,若顶点i与j都与同一条边有关联,则对应的邻接矩阵中aij=1.
由图2可得到关联矩阵与邻接矩阵之间的转换如下所示:
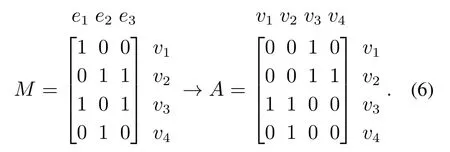
矩阵维度较大时,将导致M与A之间的转换复杂繁琐.由第2.1节可知通过计算邻接矩阵的n次方运算,即可得到通过n步连通的顶点.将这一思想引用到关联矩阵中同样适用,通过计算M2可以得到从该顶点出发2步之后到达的顶点,得出顶点之间的关系,通过上述例子验证.计算M2得到如下方阵:

按照关联矩阵作图,不同于常规作图把边当做顶点之间的连线的方式,而将边也当做一个顶点,顶点与边之间有关系的用线连接,例如e1点与v1和v3两点分别用两条线相连,如图3所示.
由图3分析可知,图中边具有无向性,从v1出发走两步可到达顶点v3,v1到达e1之后可返回v1,故v1两步可达顶点有v1,v3;同理,从v2出发分别经过e3,e2到达v3,v4,还可通过这2条路径返回v2.由M2可知v1和v3之间有1条通路,v2和v2之间有2条通路,与图3描述一致,得出结论计算M2可以得到顶点之间的关系.
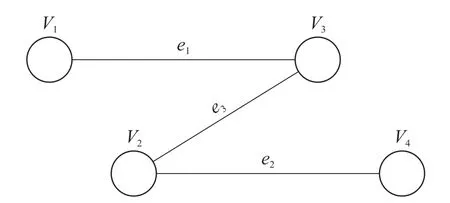
图2 简单无向图Fig.2 Simple undirected graph

图3 边与点之间联系Fig.3 Relation between edges and points
图中从vi出发到达ei消耗一步之后,剩下的一步到达自身或其他vi,故提出M2相当于邻接矩阵的自身可达和一步可达之和A+I的假设.因最终要得到顶点之间的关系而无需知道几条路径,故可将M2中非0元素全部置为1,M2和A+I分别表示如下:
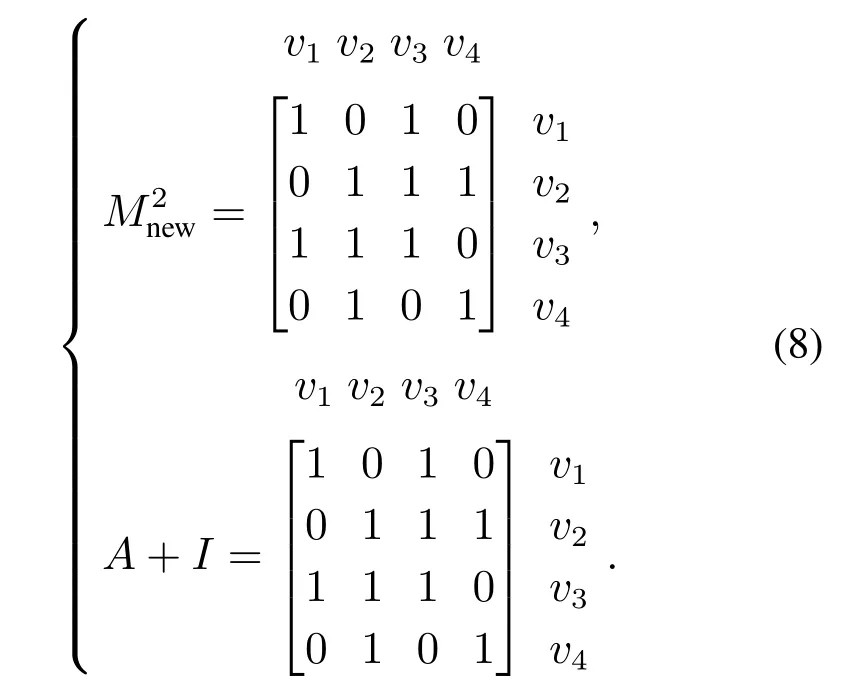
4 基于图论对多变量双层预测控制系统的分解
在双层结构MPC中,通过分解多变量进而实施分散控制可减少计算量,当变量数目较多时如何快速便捷的分解显得尤为重要.在大系统理论中基于邻接矩阵系统结构模型分解得到系统的多级结构模型[23–24],同时提出利用关联矩阵描述动态系统的结构,建立状态、输入和输出的分块矩阵.受此启发,本文直接利用关联矩阵表示MV 和CV 之间关系,通过计算M2快速变换为邻接矩阵,进而计算可达矩阵再对多变量进行分解,并应用在双层结构预测控制中.
4.1 多变量系统的分解
在描述过程模型时,通常用传递函数模型体现MV 与CV 关系.将传递函数矩阵G变成一个0–1矩阵,0代表该操作变量MV 与被控变量CV 无关,1为有关系,此时G可看做一个描述MV 和CV 的关联矩阵M(G),MV 视为边,CV 视为顶点,反之也可以.但是这个矩阵并不是标准意义的关联矩阵,因为在标准的关联矩阵中一条边只连接两个顶点,而一个MV 可控制一个或多个CV,故M(G)中的一条边可能对应一个或多个顶点情况.利用第3.4节中方法将M(G)快速转换为邻接矩阵A+I(G),得到MV 之间的关系(CV 做边,MV 做顶点),或是CV 之间的关系(CV 做顶点,MV 做边).根据式(5)计算得到可达矩阵P(G),寻找矩阵中每一列所有不为零行对应的顶点子集,具有相同的不相交顶点子集划分成一个子系统,一个多变量复杂系统就分解成若干个独立的变量较少的子系统.多变量系统分解过程步骤如下:
1) 将描述MV 与CV 关系的传递函数模型转化为关联矩阵M(G),传递函数中不为0元素用1代替,假设M(G)中行代表MV,列代表CV;
2) M(G)和A+I(G)的快速转换,计算M(G)MT(G),MT(G)M(G)转换成MV,CV 的邻接矩阵(A+I)M(G),(A+I)C(G);
3) 将(A+I)M(G)和(A+I)C(G)根据式(5)计算求出可达矩阵PM(G),PC(G);
4) 寻找PC(G)中每一列不为0所在行的CV,相同的不相交CV 即为同一个子集;按照相同方式处理PM(G),将MV 划分若干子集;
5) 按照划分的MV,CV 整理关联矩阵M(G),即可得到不同的MV 子集与其对应的CV 子集,该多变量大系统分解成多个变量较少的子系统.
4.2 多变量双层结构预测控制分解
双层结构预测控制上层基于优先级策略对稳态目标计算过程进行可行性判定与软约束调整,其计算量较大,若将该优化问题利用图论方法分解为若干个优化问题,则可减少计算量.本文仅对下层优化问题采用基于图论的分解方法,分解后的系统采用分散控制,上层仍采用集中控制.
以有约束的多变量的双层预测控制中的动态控制层为例说明,假设将该多变量系统通过第4.1节的方法分解为n个子系统,每个子系统里含有的MV 和CV不一定,用qi和zi分别代表子系统中MV 和CV 的个数,则在线优化问题可以如下描述:

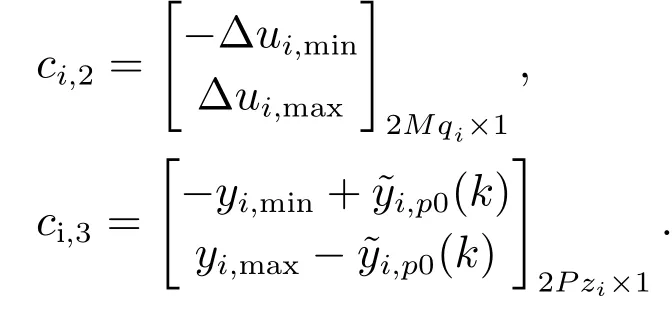
4.3 多变量双层结构预测控制分解
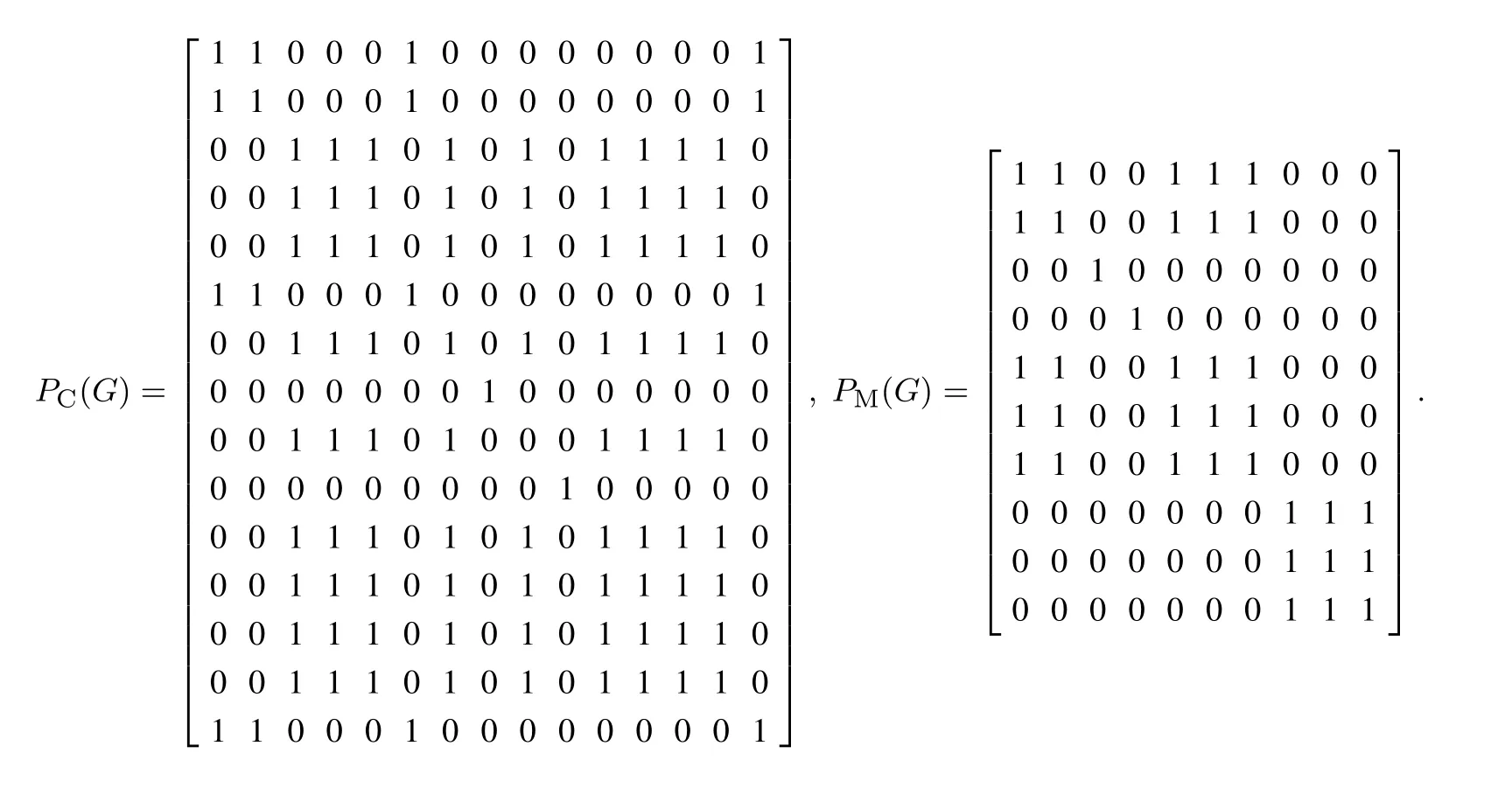
为更好的阐述第4.1节中的分解方法,用某项目的空分装置先进控制系统举例说明.由图4可知,行为MV 共10个,列为CV 共15个.MV 与CV 有关系的方格内有图像,无关系为空白格,由此得到关联矩阵M.
由M分别求出邻接矩阵A+IC(G),A+IM(G),进而分别计算得到可达矩阵PC(G),PM(G),见附录1.由可达矩阵可知,CV 划分了4个子集:

根据子集顺序整理关联矩阵,为了更清晰的观察与之间的关系,将它调整为对角线形式M′.

综上得出如下子系统划分:{CV1,CV2,CV6,CV15}对应{MV3};{CV10}对应{MV4};{CV8}对 应{MV8,MV9,MV10};{CV3,CV4,CV5,CV7,CV9,CV11,CV12,CV13,CV14}对 应{MV1,MV2,MV5,MV6,MV7}.将上述的多变量系统,快速便捷的分解为4个小的子系统.
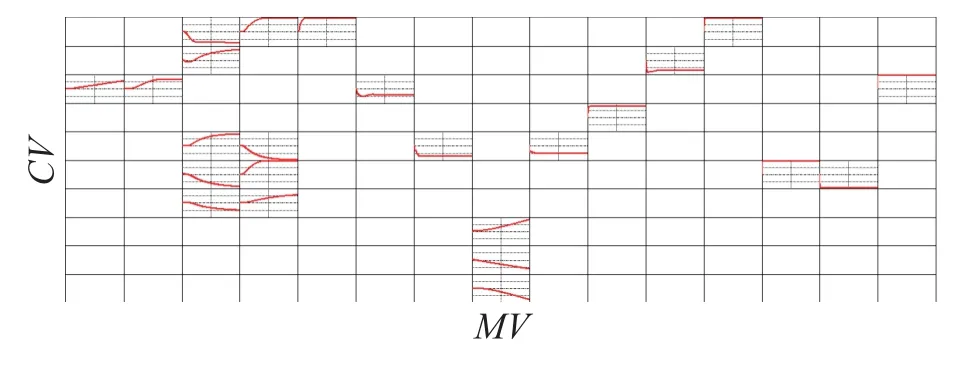
图4 某空分项目变量关系Fig.4 Variable relationship of an air separation project
5 仿真实验
针对多变量有约束的双层结构预测控制,本文基于图论对多变量系统进行分解,稳态计算层采用集中控制给出整体的稳态值,动态优化层采用分散控制.仿真实验6入6出系统为例,系统采用整体集中控制和稳态计算层集中控制动态优化层分散控制的两种策略.假设实验使用的模型是重油分馏塔的过程模型的变形,模拟一个模型较大的化工过程,传递函数模型见式(12).
将传递函数矩阵模型用关联矩阵表示,得到以行为点列为边M(G),点代表操纵变量u,边代表被控变量y.由第3.4节可知通过计算M(G)MT(G),MT(G)M(G)能快速得到点之间、边之间的邻接矩阵,进而通过式(5)分别求出点、边的可达矩阵,由此可表示出有关联的操纵变量,整理得到如式(13)的0–1对角线矩阵,最终将其替换回原传递函数对应的数据.因此可将操纵变量划分为3个子集:{u1,u4,u3},{u2,u6}和{u5}.

实验参数如下:输出约束上下限为yh=[0.6 0.6 0.6 0.6 0.6 0.6], yl=[−0.6 −0.6 −0.6 −0.6−0.6 −0.6];输入约束上下限uh=[0.5 0.5 0.5 0.5 0.5 0.5], ul=[−0.5 −0.5 −0.5 −0.5 −0.5−0.5];模型长度N=600;采样间隔是2;仿真时间K=200;选取6组预测时域P和控制时域M进行实验,详细参数见表1.
实验结果如图5所示,绿色虚线为无分解的,蓝色实线为有分解的,红色点划线为稳态值,其中横坐标轴为仿真时间,纵坐标轴为被控变量.
从图5中分析可知,对于6i6o系统无分解情况下,由于有时无法求出最优解个别输出无法跟踪稳态值,有分解的情况均能跟踪稳态值.对比二者运行时间如表1所示.

表1 无分解和有分解运行时间对比Table 1 Comparison of operation time without decomposition and with decomposition

图5 6i6o有分解和无分解系统输出对比Fig.5 Output comparison of 6i6o system with and without decomposition
由于上层仍然采用集中稳态优化,下层采用分散动态控制,运行时间为程序的整体结束时间.从上述结果分析,对于6i6o系统,在预测时域和控制时域较小时,有分解的和无分解时间相差很小;当M=25,P=50时,无分解的运行时间比分解的运行时间长,分解系统的优势随着规模增长愈加明显,到第2组仿真时无分解的时间大约是有分解的2倍.由于仿真实验受电脑内存影响,只能做到尽量保证运行内存空间一致,因此为了较好的体现分解与无分解效果,实验假设模型长度、预测时域和控制时域都较大,6i6o系统仿真证明了本文所提策略能减小计算量、减少运行时间,若是将其应用在更大型的系统中效果将更加明显.本文利用图论分解传递函数的控制变量,本质上将没有耦合的变量分离开,从理论上其控制性能并未降低,但是在优化求解过程中由于条件限制等原因,造成集中控制和分散控制求解有误差,从而导致最终结果不同.
6 结论
在双层结构预测控制中,由于变量数目多导致优化问题计算复杂,故将一个多变量系统分解成若干子系统.本文针对多变量大系统分解问题,提出利用关联矩阵描述传递函数模型中MV 和CV 之间关系,快速转换为邻接矩阵AC(G),AM(G),通过计算可达矩阵PC(G),PM(G)梳理变量之间的关系,从而能有效快捷的分解多变量大系统,并将此应用到双层结构预测控制中,上层采用集中控制下层采用分散控制,并对比常规上下层均集中控制的方法,验证基于本文提出的分解策略能够减小计算量,减少运行时间,为多变量系统的预测控制分解方式提供一种思路.
附录