定值和随动单闭环系统传感器故障诊断

那文波,高 宇,李 明,刘甜甜

(中国计量大学机电工程学院,浙江杭州 310000)

1 引言

定值和随动单回路闭环控制系统在生产中应用广泛,大致占控制系统的90%左右.传感器处在反馈回路当中,是构成闭环控制的主要单元,由于闭环系统的实时控制作用,使得其故障诊断变得复杂[1–2].

故障诊断技术可以分为3类方法[3–4].第1类方法是基于解析模型法,主要针对于可以建立精确数学模型的控制对象,例如参数估计法[5];第2类方法是基于定性经验法,通过先验知识建立起非量化的故障判断依据,例如专家系统[6]和故障元等效树法[7];第3类方法是基于数据驱动法,不依赖于控制对象的解析模型,利用实时数据在线处理分析故障类型,或者根据大量已知样本总结出故障特征从而进行推理,例如卡尔曼滤波[8]、神经网络[9].

目前基于数据驱动的故障诊断方法是研究热点[10].如文献[11]根据小波分析思想构造新型机械设备故障诊断装置;如文献[12]采用学习矢量量化(learning vector quantization,LVQ)神经网络作为模式分类器进行故障处理;如文献[13]利用主成分分析(principal component analysis,PCA)方法以及神经网络方法,对R¨ossler混沌方程预测仿真算法.

针对闭环系统传感器故障诊断问题,如文献[14]提出一种基于子空间识别和卡尔曼滤波技术,采用平均值推导、广义似然比检测(generalized x likelihood ratio test,GLRT)等方法处理残差来进行故障检测,但不能较好的处理误差以及检测慢漂移故障;文献[15]针对闭环系统传感器故障诊断问题,提出一种用于四旋翼无人飞行器加速度计和陀螺仪故障同时发生的故障检测与隔离以及故障偏差值估计的非线性诊断方法;文献[16]针对闭环系统中的传感器故障,提出了基于Kullback-Leibler(KL)距离的微小故障在线检测与估计方法;文献[17]分析故障情况下系统残差的一步转移方程递推表达式,研究闭环系统故障情况下估计误差信号和残差信号的动态演化规律;文献[18]针对牵引电机闭环控制系统,考虑电机运行过程中的谐波干扰情况,基于闭环控制策略的故障诊断方法对传感器进行故障诊断,但该方法若对转速变化的复杂瞬态过程中发生的故障进行诊断,则需要更为精确的数学模型.

本文的主要贡献:一是提出了一种适用于定值和随动单回路闭环系统的传感器故障诊断方法;二是基于定值和随动单回路闭环系统正常和故障动态特性分析和数据驱动方法,建立了故障诊断模型,并给出了利用实时数据标定故障诊断模型的流程;三是所提出的方法,一定程度上抑制了随机噪声和系统及环境固有噪声的影响,适应缓慢漂移故障的诊断,诊断时间短实时性强,并方便工程组态实现,通过实验验证了方法的可行性和故障诊断的高准确度.

2 控制系统正常和故障动态特性分析

本文以单容对象的定值和随动单回路闭环系统为例,如图1所示.其中:Ksor是传感器无故障时放大系数;kKsor为乘性故障模块,k为乘性故障增益;Ksor+a为加性故障模块,a为加性故障偏差;通过模拟机械开关实现了乘性故障模块、无故障模块和加性故障模块之间的切换.

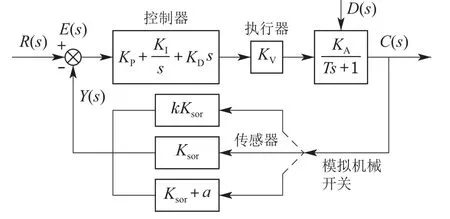
图1 单回路控制系统方框图Fig.1 Single loop control system block diagram

系统无故障状态下的传递函数:

其中:G(s)=G1(s)G2(s)KV;定值系统输入信号R(s)为一恒定值,随动系统中R(s)为一随时间变化值,从上述式(1)–(3)可以看出当不同系统发生不同故障时,系统的动态响应不同,下面介绍利用不同故障时系统的动态响应特征的故障诊断方法.

3 故障诊断方法

以传感器为故障诊断对象,基于动态数据流实时趋势的特征值提取建立故障诊断模型.解决方案具体分为故障监测、故障估计和故障分离.

3.1 故障监测

数据残差是一个判定标准,可以用于统计系统发生故障时的边界值

其中:e为残差,A为可观察数据值,A∗为期望数据值.当系统采样周期为T,数据点总数为N,选取数据窗口大小t(数据点n),则有

采用堆栈结构将新采集的动态数据填充进窗口并剔除最早的数据,设共有m个数据窗口,则

数据的窗口残差和由该窗口内所有数据点残差相加取绝对值得到,设Ei为第i个窗口残差和,那么

式中:Ai为第i个实际数据点,为第i个期望数据点.

假设正常数据残差和满足正态分布,采集l组正常数据的最大残差和,计算l组数据最大残差和平均值

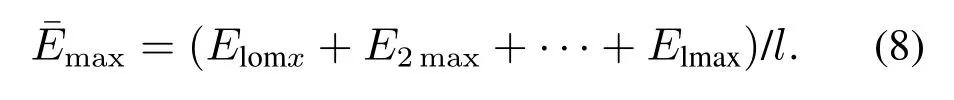
标准差为

将2σ作为去除异常数据的方法,则故障发生时残差和

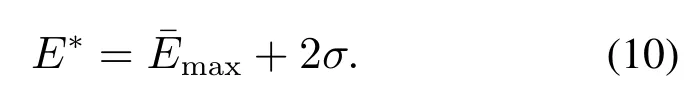
故障监测方法:即是将窗口残差和与阈值作比较,若超出了阈值范围,则判断系统发生了故障,反之系统属于正常运行状态.

3.2 故障估计

根据故障监测可以将有效诊断数据范围隔离在一个数据窗口内,即得到故障窗口数据,其中变化率最大(i)的点i对应的时刻即为故障发生时刻.

定值系统加性故障估计方法:当系统的故障类型为加性故障时,此时加性故障偏差a为

当a的符号为正时,系统故障值为增量,反之为减量.

定值系统乘性故障估计方法:当系统的故障类型为乘性故障时,此时乘性故障增益k为

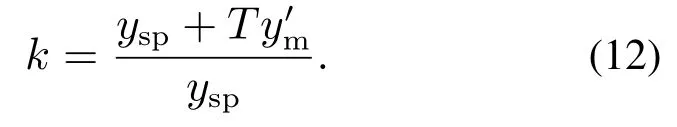
当k >1时,系统故障值为增量;当k <1时,系统故障值为减量.

式(11)–(12)即为定值系统故障估计模型.

随动系统加性故障估计方法:当系统的故障类型为加性故障时,此时加性故障偏差a为

随动系统乘性故障估计方法:当系统的故障类型为乘性故障时,此时乘性故障增益k为

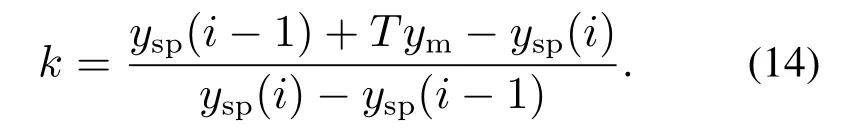
式(13)–(14)即为随动系统故障估计模型.

3.3 故障分离

系统发生不同强度的同类故障或发生相同强度的不同类型故障时,系统的初始响应斜率均不同,基于此实现故障分离.

由最小二乘法拟合方程

式(15)为一元线性回归方程模型,其中β0和β1为回归方程系数.

选取故障数据窗故障发生时刻开始的数据变化最为明显的数据集,根据最小二乘法得到这段时间内数据动态趋势的拟合方程

对系统的加性故障状态和乘性故障状态不同强度的模拟动态数据拟合处理,将式(16)中一次项系数作为提取到的特征值EV:

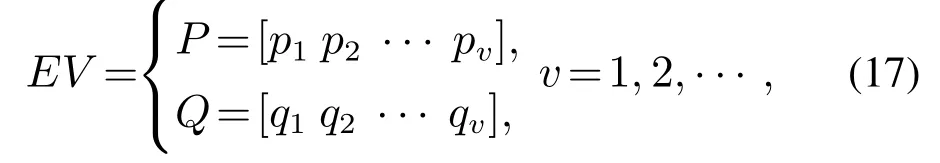
其中:P为加性故障特征值,Q为乘性故障特征值.再次采用一元线性回归法对不同故障类型的一次项系数进行拟合,以加性故障偏差作为自变量,加性故障一次项系数作为因变量,得到加性故障特征值拟合方程

同样得到乘性故障特征值拟合方程

在系统发生故障时,基于故障估计分别得到加性和乘性的故障强度,将加性故障偏差和乘性故障增益代入相应拟合方程中得到相应的.

式(16)(18)–(19)即为故障分离的静态模型,实际应用时要结合实际系统在线数据进行标定.

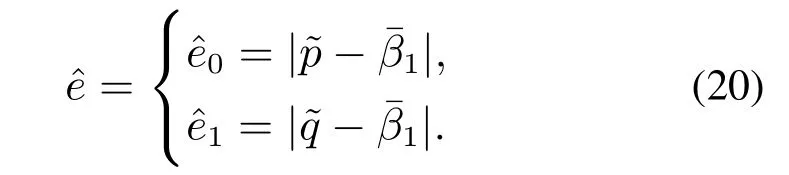
较小者视为有效结果,由此判断故障类型为加性故障或者乘性故障.

式(20)即为故障分离的诊断模型.

3.4 在线标定及故障诊断流程

实际工程应用中传感器系统在线标定及故障诊断的流程图如图2所示.

4 验证实例

验证基于四容水箱的“复杂过程系统创新实验平台”,该平台将OPC服务器连接到下位机PLC,MATLAB/Simulink虚拟控制器能够通过PID运算进行定值或随动单容液位对象的单回路控制,结合组态Wincc监控界面的实时监控和MATLAB中Workspace的在线动态数据进行实时数据分析和建立诊断模型.通过调用Simulink函数编写程序生成M文件动态链接到MATLAB软件中实现故障诊断方法的验证.通过实验可知一般在线诊断时间为200 ms.

4.1 在线数据采集

实验中设最终期望液位值为10 cm,采样周期Ts=0.5 s,单次实验中设备运行时间设定为1000 s.定值系统设定输入幅值为10 cm的阶跃信号,零时刻开始输入信号;随动系统设定输入斜率为0.01 cm/s的斜坡信号,零时刻开始输入初始值为零的信号.

4.1.1 加性故障状态

选取500 s时刻加入大小分别为±2.0 cm范围内不同强度的加性故障.如图3所示为随动控制系统,以加性故障偏差为−1.0 cm为例,得到加性故障状态下的系统响应曲线.

图2 在线标定及故障诊断流程图Fig.2 Flow chart of on-line calibration and fault diagnosis

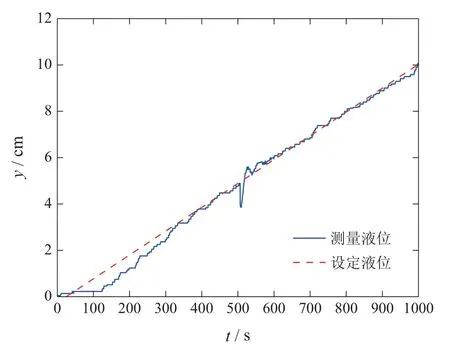
图3 随动控制系统加性故障−1.0 cm液位响应曲线Fig.3 Additive fault −1.0 cm level response curve of servo control system

4.1.2 乘性故障状态

在其他参数保持不变的情况下,对于乘性故障,同样在500 s时加入增益分别为0.8∼1.2范围内不同强度的乘性故障,可以采集到乘性故障数据.

4.2 实时故障监测

以随动系统为例,观察各种类型故障响应曲线可知系统从开始发生故障到系统自身调节到设定值附近的时间为25 s,设定t=25 s为数据窗口大小,则每个窗口数据点n为n=t/T=50.

一次实验有N=2001个数据,共有m个数据窗口

根据加窗残差和的方法,求得多组正常无故障状态下数据的最大窗口残差和,为集合EMax:

根据式(8)–(9)得到这10组数据的平均值及标准差

由式(10)确定故障阈值E∗=4.6259.

对故障诊断方法灵敏度做边界测试,确定实时数据的漏检情况.同时对多组不同故障强度的情况进行故障监测,在随动控制系统中当加性故障偏差在设定值的0.8%范围外时,乘性故障增益在设定值的1.8%范围外时,故障监测均未出现漏检情况.

对于定值控制系统,这种方法同样可以达到故障监测的目的,加性故障和乘性故障大小均在设定值的0.8%范围外时,故障监测均未出现漏检情况.

4.3 实时故障估计

以随动系统为例,当发生乘性故障1.20时的变化率曲线如图4所示,可以判断故障发生时间约为500 s.

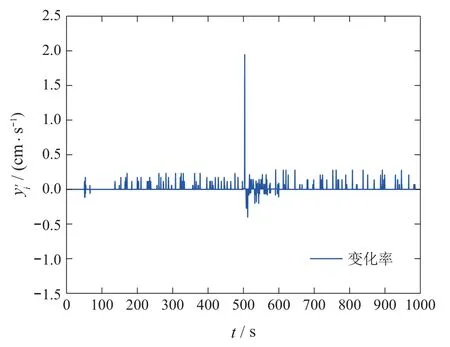
图4 随动控制系统故障状态下液位变化率Fig.4 Level change rate of servo control system

在期望值的5%范围内,选取多组加性故障和乘性故障进行实验,表1和表2给出了故障估计验证结果.

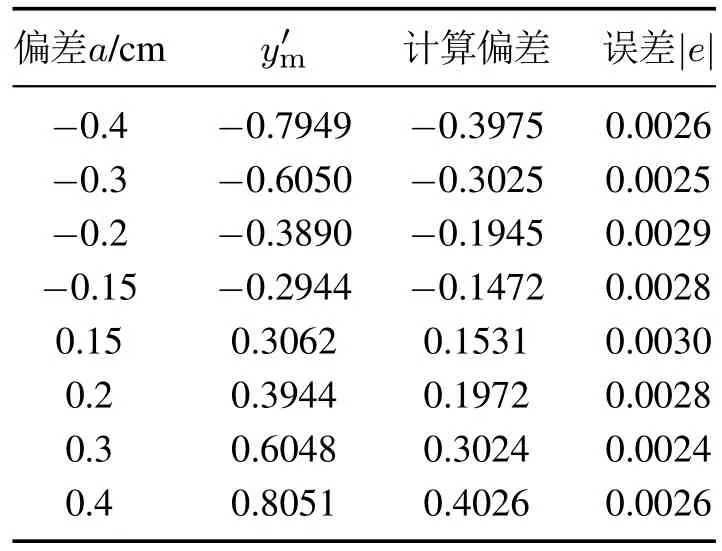
表1 加性故障估计验证Table 1 Additive fault verification

表2 乘性故障估计验证Table 2 Multiplicative fault verification

计算可得加性故障定值精度2.0%,乘性故障定值精度2.2%.

对于定值系统,同样在期望值的范围内进行故障估计实验,得到加性故障定值精度1.8%,乘性故障定值精度2.0%.

一般的系统在强故障情况下诊断精度高,可以看出在弱到5%故障强度范围内也有很高的诊断精度.

4.4 实时故障分离

定值和随动系统故障分离的区别在于,故障发生后系统调节过程的特征不相同,需要根据实际的实验结果分别得到定值和随动系统的拟合曲线,进行故障分离.当确定故障发生后,根据最小二乘法计算随动控制系统中不同类型故障下发生不同强度故障时的数据动态趋势拟合方程,如表3、表4、表5和表6所示为32组实验的拟合方程的一次项拟合系数以及拟合曲线的RMSE.

以表3为例,根据加性故障偏差a<0的一次项拟合系数得到不同程度故障状态下的拟合函数曲线如图5所示.同样对表4、表5和表6中的数据分别进行二次拟合,如表7不同故障状态下拟合函数.

根据表7的拟合结果进行分析,r2→1,RMSE →0,数据较好地拟合了对应的故障响应.如表8和表9所示为故障分离方法的验证结果.

表3 加性故障偏差小于0的一次项拟合系数Table 3 Fitting coefficient of first term with additive fault deviation less than 0

表4 加性故障偏差大于0的一次项拟合系数Table 4 Fitting coefficient of first term with additive fault deviation greater than 0

表5 乘性故障增益小于1的一次项拟合系数Table 5 Fitting coefficient of first term with multiplicative fault gain less than 1

表6 乘性故障增益大于1的一次项拟合系数Table 6 Fitting coefficient of first term with multiplicative fault gain greater than 1

表7 二次拟合结果分析Table 7 Analysis of quadratic fitting results

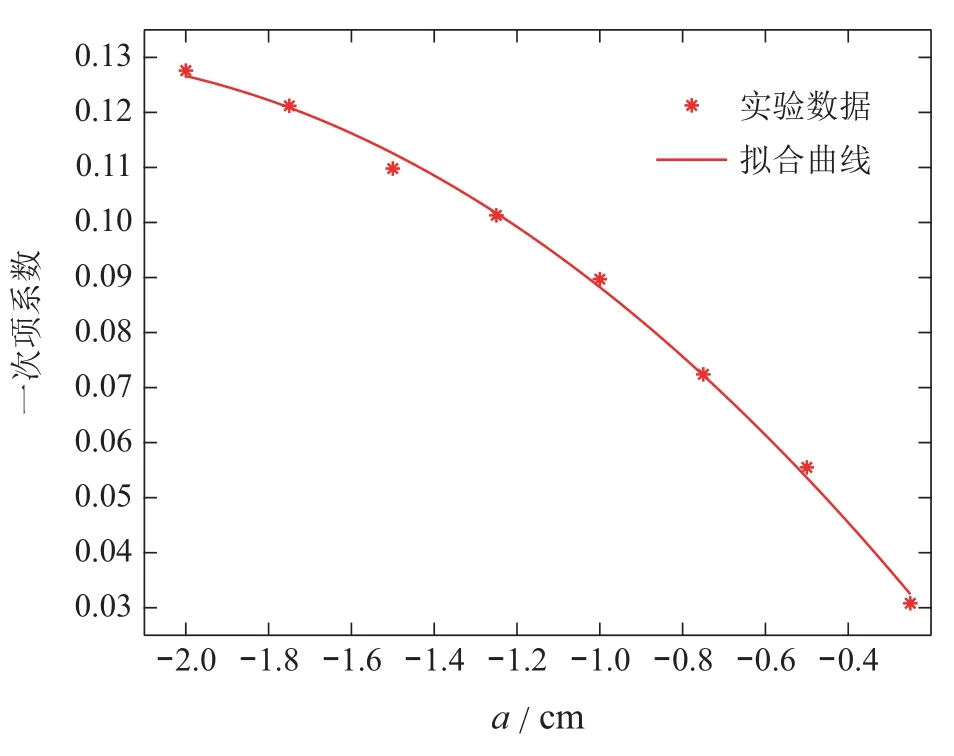
图5 同程度故障状态下的二次拟合曲线Fig.5 Quadratic fitting curve under different fault conditions

表8 加性故障分离验证结果Table 8 Validation results of additive fault isolation

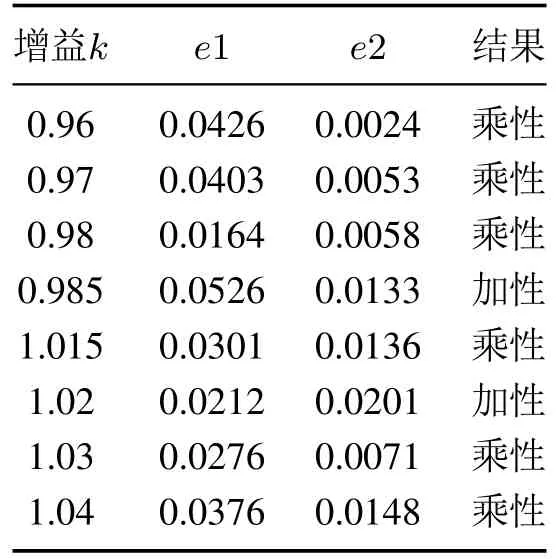
表9 乘性故障分离验证结果Table 9 Validation results of multiplicative fault isolation

可见,当随动控制系统传感器发生的故障大小在偏离期望液位值的2%以内时,不能分离.对于定值系统,同样验证得到故障在偏离期望液位值的1.5%的范围内,不能分离.

综上所述,基于动态趋势的随动系统传感器故障诊断的故障检测强度死区是1.8%,故障估计精度为2.2%,故障分离死区是2.0%;对于定值系统,故障诊断的故障检测强度死区是0.8%,故障估计精度为2.0%,故障分离死区是1.5%.验证了方法的有效性和诊断的高精度[17].

5 结语

定值和随动单闭环系统传感器故障诊断,以一阶定值和随动闭环控制系统中的传感器为故障诊断对象,基于数据驱动的思想,利用系统正常和故障动态特性分析,建立了系统故障监测、故障估计和故障分离的静态模型,并给出了在线应用的诊断模型标定方法和诊断流程.通过实验验证了方法的有效性和诊断的高精度.

方法适用于一般的一阶闭环定值或随动控制系统传感器的故障诊断;结合在线仿真数据标定故障诊断静态模型,不需建立系统模型,避免了系统模型建立不精确的缺陷,同时也避免了环境干扰和系统其它组成部分特性的影响.考虑系统各组成部分磨损,也可采取周期性标定的方法,提高诊断系统的准确度.

工程中的噪声对故障诊断是有影响的[19],本文研究方法是基于数据动态趋势分析,选择数据窗口的长度覆盖了故障发生和随之的调节过程,监测阈值的确定采用多组数据最大残差和平均值结合标准差来择优确定,且各在线诊断模型均采用实际工程系统在线数据标定,对随机噪声和系统及环境固有噪声起到了一定程度的抑制作用,获得了较高的诊断准确度.如何进一步抑制噪声影响,进一步提高诊断准确度是下一步重点研究的问题.

工程对故障诊断的实时性有一定要求[20],造成时间滞后的原因主要有传感器测量时间、数据传输时间和故障诊断算法处理时间,本方法在实验系统实时故障诊断时间为200 ms,基本能满足一般工程系统的实时性需要.进一步提高故障诊断的实时性,也是下一步研究工作的重点之一.