波形钢腹板组合梁自振特性研究

陈 雪 松

(兰州交通大学土木工程学院，甘肃 兰州 730070)

波形钢腹板组合梁桥是一种顶板和底板由混凝土浇筑而成，而腹板是波纹状钢板的一种组合梁，具有较高的屈服强度和抗弯刚度。同时由于波纹状腹板较传统混凝土腹板轻，且梁高小，故自重小，具有很多传统箱梁桥所没有的优势，已经被广泛运用。人们对波形钢腹板的剪力滞和剪切变形做了较多研究。陈水生运用能量变分法，推导了波形钢腹板在考虑剪力滞效应情况下的翘曲位移函数[1]；Karnik Aggarwal等运用了ABAQUS讨论了腹板厚度，腹板高度，板宽对剪切屈服系数的影响[2]。但是大部分的研究涉及的都是剪力滞和剪切变形对波形钢腹板的挠度的影响，而经典梁理论没有考虑到剪力滞效应对竖向弯曲振动频率的影响，张永健根据波形钢腹板组合梁的特点，并考虑结构的剪力滞效应和剪切变形的影响，推导出波形钢腹板组合箱梁的各阶振动频率[3]；冀伟运用能量变分原理和Hamilton原理推导出剪力滞效应，剪切效应和两者的耦合效应对简支梁的弯曲振动频率的影响程度，并考虑了剪切刚度在有无修正的情况下的影响程度[4]；Liang Cao等根据E.Reissner 和 Galerkin 方法，考虑了剪力滞效应和剪切变形，推出了弯曲振动频率的精确公式，并分析了腹板波形和上翼缘和腹板的厚度对其的影响[5]。

以上波形钢腹板组合梁桥弯曲振动频率计算方法可以总结为5种方法：经典梁法、铁木辛柯梁法、欧拉梁法。因为有限元不需要太多的试验费用，并且结果较为准确，故在比对各方法后再采用有限元建立模型来分析，对比各方法的理论差异以及适用条件。

1 方法类比

欧拉梁即为经典梁理论，是忽略剪切变形对弯曲振动频率的影响的传统计算方法，其计算假设为：1)不考虑波形钢腹板的剪切变形对弯曲振动频率的影响。2)其横截面的转动与箱梁上底板和下底板的转动保持一样大小。3)箱梁的畸变和扭转忽略不计。4)材料是线弹性的。5)满足平截面假定。

(1)

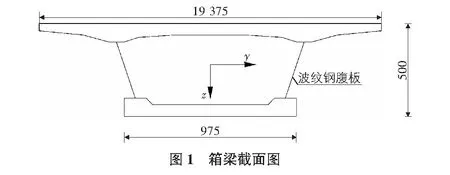
波形钢腹板组合箱梁桥的腹板抗弯刚度很小可以不予以考虑，而普通箱梁桥的弯曲振动频率是可以通过较为简单的计算得到的。张永健为了得到波形钢腹板组合箱梁桥的弯曲振动频率，将腹板的弯曲刚度取为0，箱梁截面图如图1所示。所采取的假设是上下翼缘板的纵向变形是一个三次函数，该函数沿着桥梁横向分布，且在对称挠曲时，桥梁的纵向位移符合平截面假定。

弯曲振动频率公式为：

(2)

(3)

(4)

(5)

(6)

其中，α1为考虑剪力滞效应下，弯曲振动频率的降低值；α2为考虑剪切变形条件下的降低值。

根据铁木辛柯梁理论，由于波形钢腹板组合箱梁桥的腹板厚度较传统箱梁桥薄，剪切变形对其弯曲振动频率影响较大，不可忽略。其计算的假设条件为：1)只考虑波形钢腹板剪切变形。2)其横截面的转动与箱梁上底板和下底板的转动保持一样大小。3)箱梁的畸变和扭转忽略不计。4)材料是线弹性的。5)满足拟平截面假定。

其计算公式为：

(7)

冀伟运用能量变分原理和Hamilton原理，推导了计算波形钢腹板组合简支箱梁桥的弯曲振动频率的公式，其中运用到的假设是：1)在桥梁纵向方向，波形钢腹板有着褶皱效应，其纵向的抗弯作用可以忽略不计，因此假设纵向弯曲应变能为0。2)波形钢腹板组合梁桥因为有较为明显的剪力滞效应，使得当发生竖向的弯曲变形时，平截面假定将不再适用。

(8)

纵向弯曲应变能因为极其微小几乎可以忽略不计的纵向抗弯性能而假设为0，故Cao Liang采用了如下公式计算振动频率：

(9)

(10)

通过比较五种计算方法的计算公式和假设条件可以得到五种方法的异同点。相同点为假设材料是线弹性和不考虑箱梁的畸变和扭转对其竖向振动频率的影响，而主要的不同点为有没有将剪力滞与剪切变形考虑在内。由于腹板承担了绝大部分的剪力，这导致在计算振动频率时，剪切变形的影响较大，欧拉梁理论并没有将剪切变形和剪力滞考虑其中，因而会与实际测量值相差较大。铁木辛柯梁仅考虑了剪切变形的影响，其他三种理论均考虑了剪切变形和剪力滞效应的影响。其次是有着不同的截面假定，欧拉梁法假设满足平截面假定，铁木辛柯梁假设箱梁满足拟截面假定，即纵向刚度忽略不计，将上下翼缘板的纵向线应变连接起来，这样就可以假设满足平截面假定了。

2 算例分析

按照1∶4的比例修建波形钢腹板试验梁，其总长为9 970 mm，计算跨径为9 745 mm，其中设置5道厚度为75 mm的中横隔板和2道厚度为56.25 mm的端横隔板。支座的中心线和梁端之间的距离为1 125 mm，腹板的厚度为2.5 mm。

模型取用C50的混凝土材料，其弹性模量为3.45×104MPa，泊松比为0.167。腹板用的是Q345钢，其弹性模量是1.95×105MPa，泊松比是0.3。模型用ASTM A416-87a标准的低松弛预应力钢绞线，其270级的标准强度是1 860 MPa。模型采用R235钢筋作为体内普通钢筋。

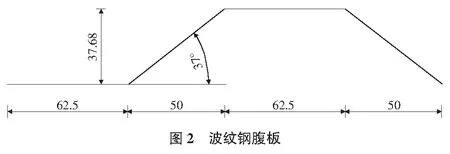
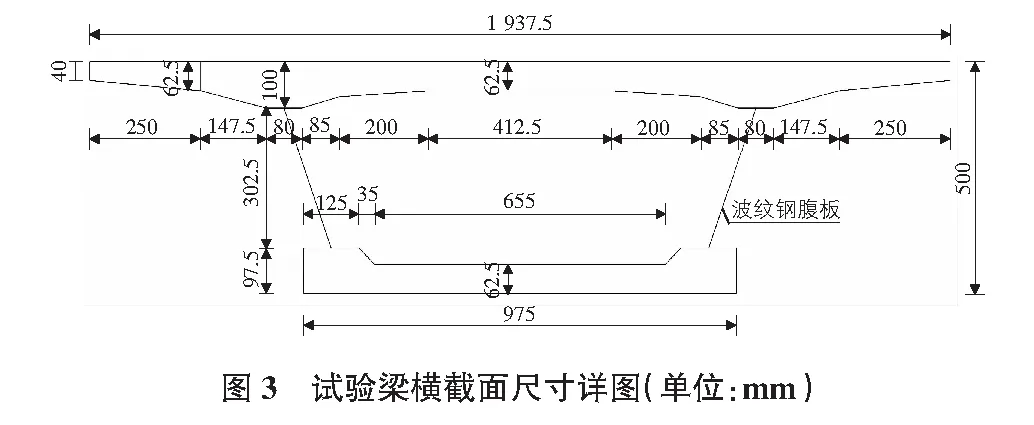
该模型所用的波形钢腹板的尺寸见图2，该横截面的详细尺寸见图3，建立的ANSYS模型见图4。

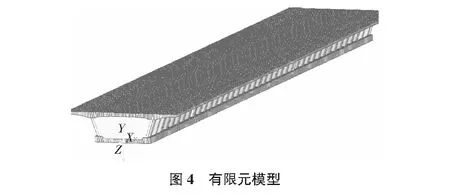
分别用这五种计算方法计算出的弯曲振动频率列于表1。

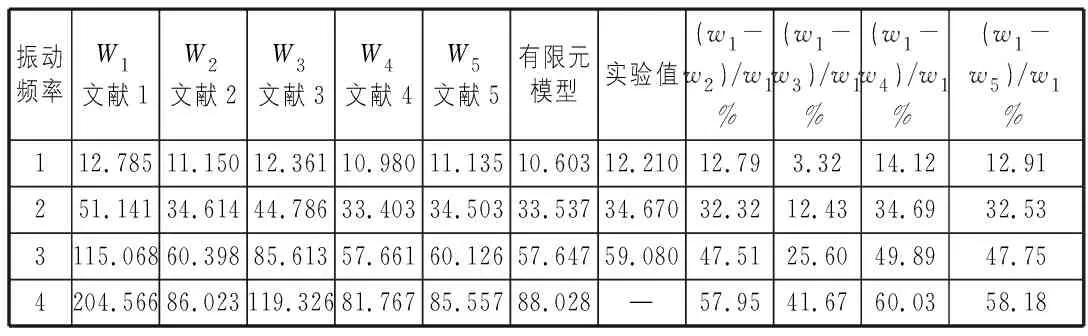
表1 各频率对比

3 结语

1)随着振动频率阶次的增加，剪切变形和剪力滞效应对自振频率的影响逐渐增大，与真值的差值较大，故经典梁理论已经不适用，需进行修改理论公式。2)冀伟运用能量变分原理和Hamilton原理推导的计算公式，其与有限元值拟合最为精确，故纵向的抗弯作用忽略不计是符合理论的，同时剪力滞效应对自振频率的影响较大，需要予以考虑。