基于模态分离的圆管裂纹超声导波无损检测

黄 吉，孙明健，刘 旸，李选会，吴宝剑，张庆标，吴旻昊，尹晓虎

(1.哈尔滨工业大学 信息科学与工程学院，威海 264209；2.32286部队，济南 250024)

超声导波技术是近年来迅速发展的无损检测技术之一，相较于超声检测、涡流检测、渗透检测等无损检测方法，具有传播距离远、全范围覆盖检测、可非接触检测等优点，已成为目前无损检测领域的研究热点。

基于超声导波的无损检测方法的基本思想是当传播中的导波遇到裂纹或结构不连续处时，会发生反射现象[1]，其中反射产生的回波信号中包含着材料缺陷的相关信息[2]，对回波信号进行分析可以得到与缺陷相关的参数信息。但是导波在传播过程中时常伴随着多模态和频散现象[3]。其中多模态会造成不同回波信号的叠加，给信号分离带来困难；频散现象则会使检测信号加速衰减，导致检测灵敏度降低。刘胜等[4]通过对管道进行导波测量，得出超声导波无损检测技术应用在长管道上可以达到截面积损失量1%以上的检测灵敏度的结论。美国西南研究院的无损检测团队研制的基于磁致伸缩效应及逆效应的MsSR3030设备，通过激励出高纯度的T模态导波，可以达到最高0.7%的检测灵敏度。对于现在的线性超声导波检测技术，其通常以纵向模态或扭转模态导波作为检测模态，将产生的回波中与检测导波模态相同的导波信号提取出来，分析导波信号的时间与幅值的变化关系，进而实现对裂纹的检测。这种方法对于尺寸大于波长的裂纹具有较高的检测精度和灵敏度，但对微小缺陷检测时，时间和幅值的变化关系非常不明显，导致检测结果不准确。所以，单纯的线性超声导波检测方法对微小缺陷的检测能力不足。孙学伟等[5]曾用L模态作为检测模态，并通过对比有无裂纹的周向振动图来判断裂纹是否存在，从而实现对微小裂纹的检测，但文章中并没有指出确定裂纹以及定位裂纹的方法。

文章基于模态分离的思想，利用回波中的弯曲模态导波，通过对混合模态进行分离来判断微小缺陷的存在性，并进一步对微小缺陷在管道中的轴向位置进行计算；提出一种弯曲模态分离的方法，最后对一种特定参数的管道进行有限元仿真来验证该方法的可行性及裂纹定位的准确性。

1 超声导波基本理论

1.1 圆管超声导波频散方程

材料均匀的各向同性弹性空心圆管及坐标模型示意如图1所示。忽略体力的情况下根据弹性力学的知识，质点的振动位移满足Navier-Stokes方程[6]。

图1 空心圆管及坐标模型示意

(1)

式中:u为位移矢量;λ和μ为拉梅常量;ρ为材料密度;2为拉普拉斯算子;t为时间。

对式(1)中的u进行Helmholtz分解，得到柱坐标系下的三个振动位移分量。

当导波在圆管中沿轴向传播时，需满足的边界条件为：

σrr=σrz=σrθ,r=a,b

(2)

式中:srr为内外面垂直应力;srz和srq为切应力;a和b为空心圆管内外半径。

根据边界条件式(2)，求解得到以下方程组，其中D为系数行列式

|Dij|=0, (i,j=1，2,3,…,6)

(3)

当导波的周向阶数n=0时，由式(3)得到纵向模态L(0,m)和扭转模态T(0,m)，其均为轴对称模态，对于圆管圆周上的任意位置，引起的振动位移大小相等且关于z轴任意角度旋转对称;当n≠0时，得到弯曲模态F(n,m)，其中n为导波阶数，m为导波数，其为非轴对称模态，在圆周任意位置上引起的振动位移大小是不同的，振动形态与n有关。

1.2 超声导波的频散和多模态特性

在超声导波无损检测过程中，多模态和频散特性会给信号处理和缺陷辨析带来极大困难。对于同一材料的空心圆管，当其截面半径比b/a不同时，导波的频散曲线也不同。因此针对某一特定参数的圆管，绘制其频散曲线，选择合适的激励模态和激励频率是首先要解决的问题。

文章有限元仿真选取的空心圆管参数如表1所示。根据表1的数据，利用超声导波频散曲线绘制软件GUIGUW进行频散曲线绘制，频散曲线如图2所示。

表1 空心圆管材料参数

常用的检测导波模态有L(0,2)和T(0,1)。由图2可以看出，T(0,1)模态不发生频散且在很宽的频率范围内不存在高阶模态，常被用来检测轴向裂纹。因此笔者也选择T(0,1)模态作为激励模态。一般情况下，为检测微小缺陷，会选择较高的激励频率，但较高的频率会导致模态数量的增加，故选择相对较低的频率(20 kHz)作为激励频率。

图2 群速度频散曲线

2 模态分离方法

由上述内容可知，纵向模态和扭转模态都是轴对称模态，其中扭转模态没有径向位移，即弯曲模态是非轴对称模态，其振动形态随导波阶次的不同而发生变化，其中部分模态的周向振动形态示意如图3所示[7]。

图3 模态振型图

由图3可以看出，纵向模态的径向振动是沿着各自径向的，且呈轴对称分布；当n分别等于1,2,3,4时，质点的径向振动位移分别沿圆管周向具有1次,2次,3次,4次周期性。

根据上述模态振型的分析，将传感器测得的数据转换到图1中的柱坐标系O2下，对于相对位置上的传感器测得的径向位移值，利用作差法，可以消除纵向模态(n=0)和部分弯曲模态(n=2,4)，得到部分弯曲模态(n=1,3)，利用作和法时则反之。令ur1，ur2，ur3分别表示作差法和作和法的结果，建立以下等式。

(4)

式中:n为导波的周向阶次;θ为任一传感器所在半径与O1坐标系x轴的夹角，θ∈[0,2π];uf为O2坐标系下径向位移数据,ur只是uf数学运算中产生的中间量。

根据图3(b)，对圆周上任意位置，F(1,m)引起的振动位移是沿某一固定方向的，且该方向是任意的。如图4所示rf(1,m)为F(1,m)引起的位移向量，假设其与x轴夹角为γ，由于试验只记录径向位移，故记录的数据中只包含rf(1,m)的径向分量uf(1,θ),即如式(5)所示。

图4 位移矢量示意图

(5)

又根据图3(d)，截面上任意点的径向位移等于相距2π/3位置上点的径向位移。则有关系式(6)。

uf(3,θ)=uf(3,φ)

(6)

最后利用作差法

ur(n,φ)-ur(n,θ),n=1,2,3,4

(7)

将式(5)和式(6)代入式(7)，化简整理后可得式(8)。

(8)

算法流程图如图5所示,根据上述模态分离方法，可以将复杂回波中由微小缺陷产生的部分弯曲模态提取出来，再根据波包飞行时间即可确定圆管中微小缺陷的存在位置。

图5 算法流程图

3 仿真验证

3.1 有限元仿真模型

根据表1参数建立ABAQUS有限元仿真三维模型，并根据缺陷三维尺寸在圆管距离激励端500,600,2 000,3 000,3 500 mm的位置制造人为缺陷,缺陷基本尺寸为沿圆管径向2 mm，沿圆管周向1 mm，沿圆管轴向6 mm。截面积损失量为0.09%，轴向比率为0.15%，远小于常规可检测灵敏度。

选用经Hanning窗调制的5周期20 kHz单音频叠加信号作为激励信号，在空心圆管端截面外圆面均布的64个激励节点上均匀加载，激发T(0,1)模态。64个检测节点同样均布在端截面上，记录各检测节点沿管表面的法向位移数据。自收发式激励检测节点布置如图6所示。

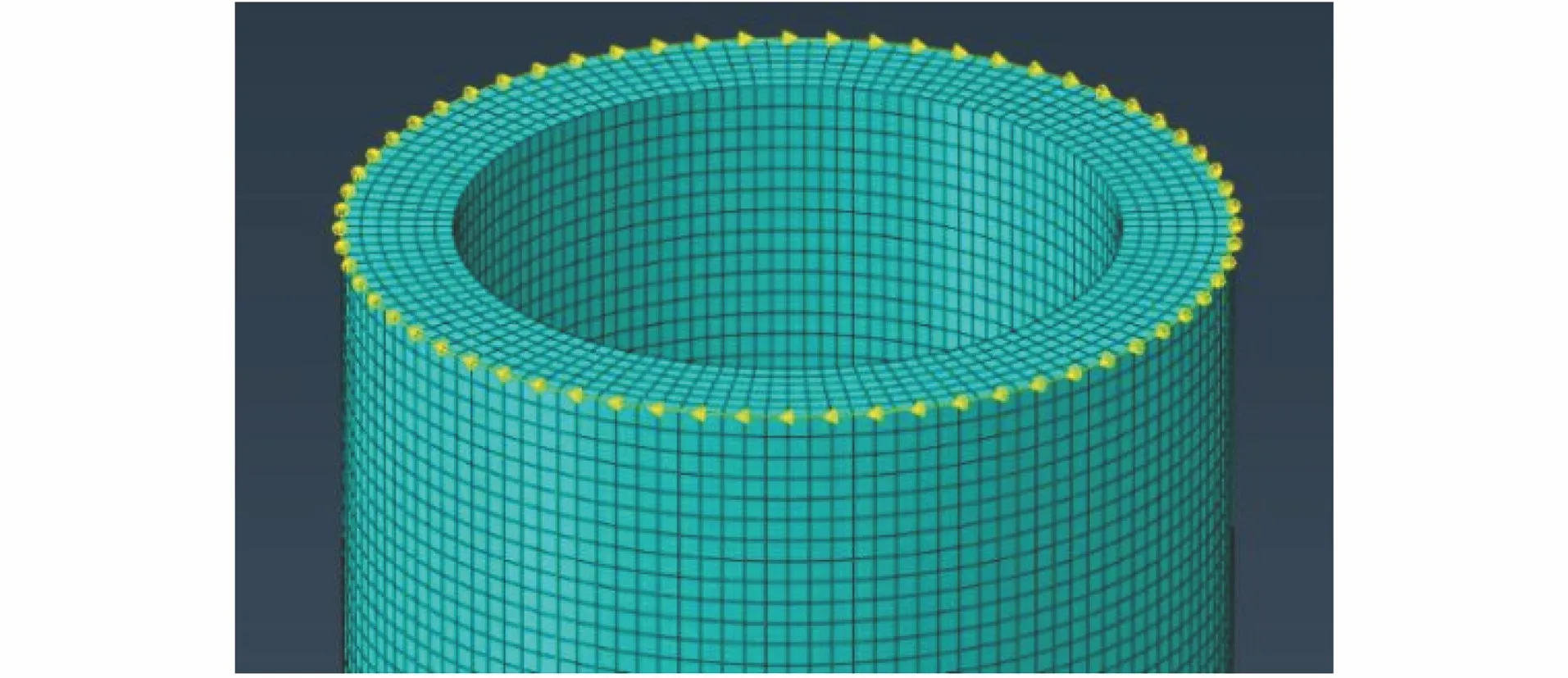
图6 信号激励检测节点布置

3.2 模态提取

记录的位移数据进行坐标变换，将其转换到图1所示的柱坐标系O2下。按照模态振型的显著特点进行数据初步分离。由于即使是两种阶次的弯曲模态混合，其波形也相当混乱，所以还需要继续对数据进行进一步分离。对于式(8)，其γ和rf(1,m)都是未知的，因此该方程对于任一节点有无数解，但F(1,m)只有一个固定的振动方向，故所有节点的解必有交点，结果如图7所示，图中横轴表示rf(1,m)大小，纵轴表示γ角大小。

图7 不同传感器上F(1,m)模态振动方向与大小的关系

为保证模态分离后结果的可靠性，数据的准确性和较高的波形还原度，将根据式(4)至式(8)，对模态分离后的数据可视化，对比记录的原始数据分析结论。任意取两时间点，画出检测节点的位移，为更好地显示出结果，在分离后的数据基础上加上了一个较小的固定值，结果如图8,9所示。

图8 F(2,m)模态分离前后振型对比示意

由图8可以看出，分离后的振型与理论相符合，但其与原始数据相差不多，结合图2可知，这是理论上该频率下导波中F(4,m)模态成分很少导致的。而从图9可以明显看出，分离前后F(3,m)模态提取程度高，结果与理论符合程度也很高。

图9 F(3,m)模态分离前后振型对比示意

根据上述方法得到的结果，可以直观地得到整个仿真过程中任意时刻检测节点的复合位移的模态构成，对分析回波中模态的成分有着至关重要的作用。

3.3 微小缺陷轴向位置判定

根据上一节的结果，模态分离的效果是理想的，分离后振型辨识度高。但要想得到微小缺陷在圆管中的轴向位置，还需对分离后的数据进行综合处理，根据波形来定位微小缺陷的位置，对于F(n,m)模态，任意时刻选取n个最大值和最小值，取绝对值求和后平均，得到波包图如图10(a)(e)所示。其中图10(a)为原始未分离信号的波包图，图10(b)、(c)、(d)、(e)分别为F(1,m)、F(2,m)、F(3,m)、F(4,m)模态的波包图。从图10中可以看出，F(1,m)和F(3,m)模态的波形波包辨析度高；F(3,m)模态的波包辨析度差，这是因为该频率下三阶弯曲模态的频散现象严重；F(4,m)模态的波包小，这是因为理论上该频率下是不存在该模态回波的，但频散现象导致回波中掺杂着少许F(4,m)模态。波包图中是包含端头回波的，但相对于端头回波，缺陷回波要更加靠前，因此并未对所有波包进行分析，而只对第一个波包，即缺陷引起的回波进行分析。单纯靠波包图只能得到回波的时间而无法确定中心频率，故文章选用复Morlet小波作为小波基，对波包图进行小波变换，结果如图10(f)(i)所示。在波形图中确定波峰的时间点，结合小波变换图中确定的相应时间点和中心频率，根据图2中对应模态在该频率下的传播速度，即可确定圆管中缺陷的轴向位置。根据上述方法进行微小缺陷的轴向位置确定，得到的结果如表24所示。

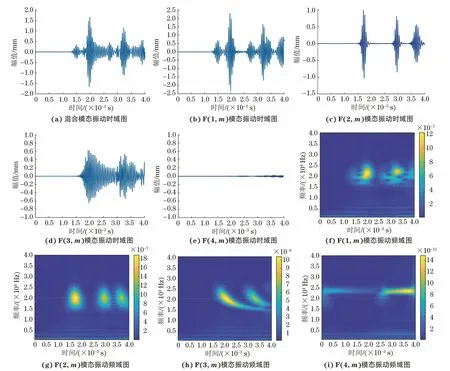
图10 各模态振动波形和小波变换

从表24中可以看出，微小缺陷的轴向定位精度高，误差在2%以内。其中F(4,m)模态导波数据不具有指导定位裂纹的意义，文章并未对其波形数据进行分析。

表2 F(1,m)模态对微小缺陷的定位结果

表3 F(2,m)模态对微小缺陷的定位结果

表4 F(3,m)模态对微小缺陷的定位结果

4 结论

基于超声导波的基本理论，分析了空心圆管中导波的频散及多模态特性，并根据特定参数绘制出频散曲线。基于模态振型幅值和相位不同的原理，通过对回波数据进行特征匹配进而实现了模态分离，并进行试验论证，得到如下结论：提出的模态分离方法在回波数据处理中效果明显，在分离后各模态振型的可视化基础上，可以看出各弯曲模态分离程度较高，与理论的符合程度较高。同时，将分离后的数据进行小波变换，结合频散曲线图，能够很好地确定微小缺陷等非轴对称结构的在圆管中的轴向位置；并且该方法在裂纹微小或激励频率较低的情况下仍然适用。