基于小波包的锅炉炉管声波信号自适应压缩感知

杨正理，史 文，陈海霞



基于小波包的锅炉炉管声波信号自适应压缩感知

杨正理，史 文，陈海霞

（三江学院机械与电气工程学院，江苏 南京 210012）

在锅炉炉管泄漏声波自动报警系统中，针对声波信号在采集、传输、处理与存储过程中存在数据规模大、传输带宽高和所需存储量大等问题，提出基于小波包的锅炉炉管声波信号自适应压缩感知方法。首先采用小波包分析方法对炉管声波信号进行多尺度分解，计算各尺度下小波包系数的数学期望，并将其作为阈值，对小波包系数进行置零处理，根据各分解尺度下的稀疏度自适应地选择最优小波包分解层数；然后对最优分解层数下的各小波包系数块按照其数学期望和信息熵进行分类，并对分类后的各小波包系数块采用不同方法进行处理。实际应用结果表明，本文方法有效减少了炉管声波信号的观察数据，提高了信号压缩率，并在相同观察次数下，降低了信号的传输带宽和存储容量，提高了信号的处理速度和重构精度。

锅炉；炉管；声波信号；信号压缩；小波包分析；压缩感知；数学期望

锅炉炉管在高温高压工作状态下容易发生泄漏事故。锅炉炉管自动报警系统是炉管发生泄漏的主要预警系统，该系统根据安装在锅炉上的声波传感器获取炉管声波，上传至上位机进行分析与处理，获得炉管当前运行状态，一般上位机存储近三年的声波信号，以备查询[1-2]。传统的声波信号采样基于奈奎斯特全采样定理，必然存在采样数据量大、传输带宽高、存储容量大及分析处理时间长等系列问题。

近年来，采用压缩感知（compressed sensing，CS）方法处理各类声波信号受到众多学者的关 注[3-4]，并取得较大成果。文献[5]比较了几种传统语音信号进行压缩感知时的观察矩阵性能，并对不同条件下选取语音信号最佳观察矩阵提出合理建议，在保证较高压缩率的前提下提高了信号的重构精度；文献[6]分析了噪声对声音信号进行压缩感知时的影响，从语音信号的观察矩阵和重构算子两方面提高了声音信号在压缩感知时的鲁棒性；文献[7]提出了一种采用压缩感知技术在信号接收端丢失数据包的情况下通过重构来恢复多媒体音频信息的新方法，并通过实验方法证实了该方法的实用性；文献[8]采用修正的离散余弦算法对语音信号进行稀疏变换，并利用语音信号在频域的结构特征来重构信号的方法，在不同帧长、不同压缩率下提高了语音信号的重构精度；文献[9]针对语音信号在压缩感知算法中存在的缺点，采用正交匹配追踪算法对语音信号进行重构，使信号的重构精度和去噪性能得到提高；文献[10]采用离散余弦算法对语音信号进行稀疏变换，并基于混沌序列和符号函数构建出一种确定性和随机性相统一的观察矩阵，使重构后语音信号的可懂度和清晰度得到大幅提高。

然而，压缩感知在声波领域的应用仍存在不足：1）采用传统变换方法，如离散余弦、离散小波等对信号进行稀疏变换时，其稀疏度不能达到最高，且容易丢失信号中的有用特征信息，造成信号的压缩率和重构精度较低；2）采用小波变换技术对声波信号进行稀疏变换过程中，当小波系数采用固定阈值进行置零处理时，过小或过大的阈值均会造成信号压缩率降低或丢失有用的信号特征；3）声波信号在其频域具有不同的结构特征，如果采用相同的处理方法会造成信号的观察数据量增大，使信号的传输带宽提高、存储容量变大以及分析处理时间加长等。

对此，本文提出基于小波包变换对锅炉炉管声波信号进行自适应压缩感知的方法。首先，利用小波包对炉管声波信号进行多尺度变换，根据各尺度下的稀疏度选择最佳分解尺度，使信号在频域的稀疏度最高；然后，根据最佳分解尺度下各小波包系数块的数学期望和信息熵对各系数块进行分类，不同类型的系数块采用不同的处理方法，降低了信号的观察数据量，提高了信号的处理速度。

1 基于小波包变换的信号稀疏变换

1.1 小波包变换原理

小波包变换的实质是小波子空间的多分辨分解过程，当给定小波函数()和正交尺度函数()时，其2尺度方程[11]可表示为

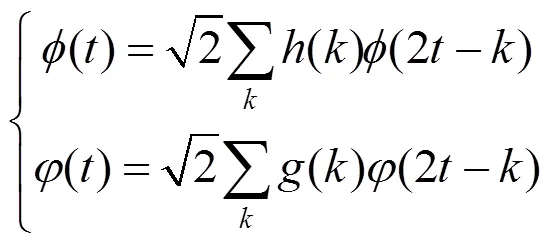
式中，()和()分别表示多分辨分析中低通和高通滤波器的系数，为时间。

对2尺度方程进行推广，可得

式中=0, 1, 2, …。

当0时，0=()，1=()。所以，小波包空间是一个满足2尺度方程的函数集合。小波包空间表达式和小波包系数的递推关系[12]可分别用式(3)和式(4)表示，

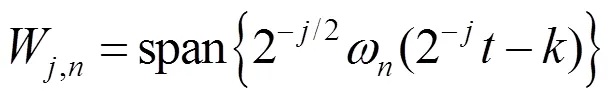
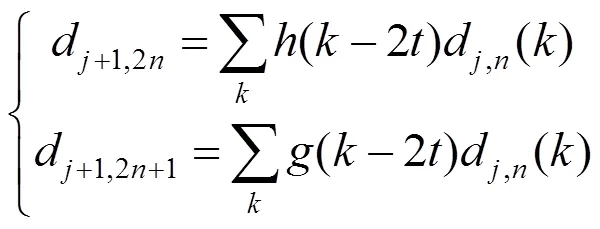
式中为尺度。

从上述分析可见，小波包分析对信号的高频部分和低频部分进行同步分解，因此具有更精细的分析性能。当分解尺度不同时，信号所表征的精细程度不同，因此，采用小波包分析信号时应选取合适的分解尺度[13]。

1.2 小波基选择

采用小波包变换方法将声波信号变换至频域进行分析。信号在频域的稀疏度越高，其压缩率和重构精度越高。将声波信号采用小波包进行稀疏变换时，信号在频域的稀疏度与所选取的小波基类型密切相关。目前，小波基类型的选择还没有统一的理论方法，需要根据经验和信号的特点，采用实验方法确定。

本文首先采用某锅炉炉管声波自动报警系统的历史数据（采样频率30 kHz，数据中间段约50%的数据为炉管发生泄漏时的故障信号，数据长度为2 048×256个采样点）中截取一段长度为256个采样点的声波信号，分别选择几种常用的小波基对其进行4尺度小波包分解，计算4尺度下小波包系数高频部分的数学期望作为阈值，对小波包系数进行置零处理，并计算置零处理后的小波包系数的稀疏度(即为零系数占所有系数的百分比)，结果见表1。由表1可见，采用Sym5小波基时的小波包系数的稀疏度最高。因此，本文选取Sym5作为锅炉炉管声波信号稀疏变换的小波基。

表1 不同小波基进行稀疏变换时的稀疏度

Tab.1 Sparsity of different wavelets used to sparse transform

1.3 分解尺度与稀疏度的关系

采用小波包对声波信号进行稀疏变换时，不同分解尺度下信号的精细程度不同，在保证较高重构精度的前提下，其稀疏度也不同。在历史数据中任意截取5段长度为256个采样点的声波数据，采用Sym5小波基进行2—6尺度小波包分解，分别计算各信号在各尺度下小波包系数高频部分的数学期望，将其作为阈值对系数进行置零处理，并计算各尺度下小波包系数的稀疏度，结果见表2。由表2可以看出，各信号段在小波包不同分解尺度下的系数稀疏度不同，不同信号段的最高系数稀疏度在各尺度下的分布也不同。所以，在实际应用中，不同的信号段必须选择合适的分解尺度，才能使其在频域的稀疏度最高。

表2 不同分解尺度下小波包系数的稀疏度

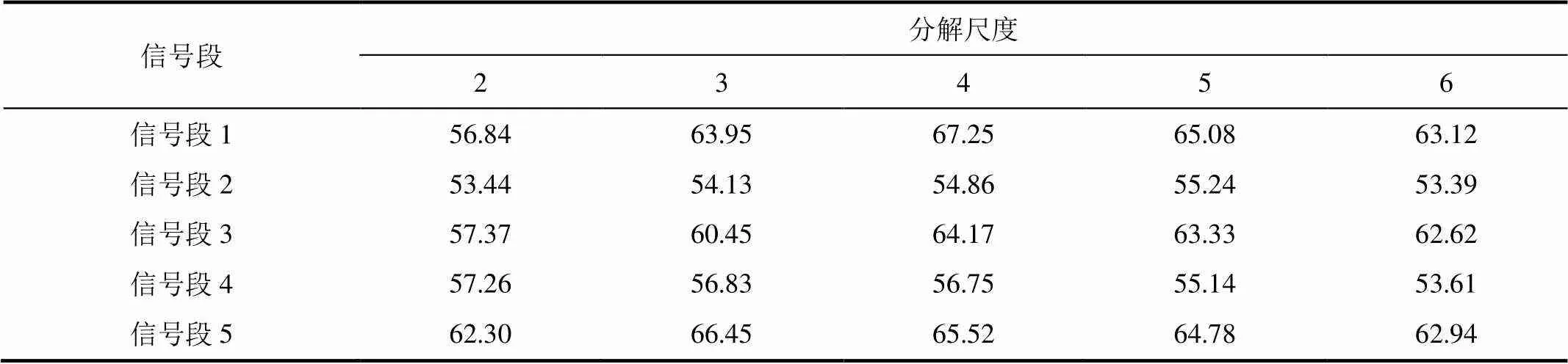
Tab.2 The sparsity of wavelet packet coefficients in different decomposition scales %

2 锅炉炉管声波信号自适应压缩感知

2.1 压缩感知原理

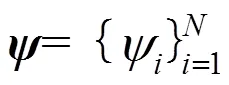
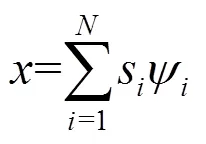
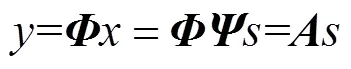
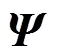
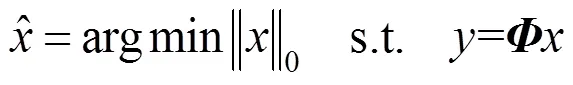
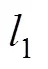
2.2 基于数学期望的阈值选取

设数据序列={x},=1, 2, …,，定义其数学期望为

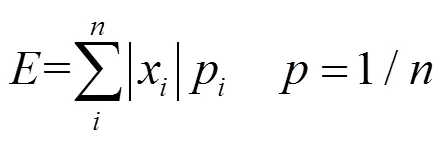
对声波信号进行小波包分解后，采用式(8)计算小波系数高频部分的数学期望作为阈值对小波系数进行置零处理，使小波包系数在足够的稀疏度下具有较高的重构精度[21]。从历史数据中任意截取一段长度为256个采样点的声波数据，采用Sym5小波基进行2尺度小波包分解，计算2尺度下小波包系数高频部分的数学期望为{19.26, 3.64, 4.02}，选取数学期望最高值19.26作为阈值，对2尺度下的小波包系数进行置零处理，即

2.3 自适应小波包变换

声波信号经小波包分解，并经置零处理后的小波包系数的稀疏度越高，信号的压缩率越高，信号的重构精度也越高[22-23]。为了保证信号具有足够高压缩率和重构精度，必须使小波包系数的稀疏度足够高。小波包系数的最高稀疏度分布在不同尺度上，为了保证足够高的小波包系数稀疏度，采用固定的分解尺度显然不合理。因此，本文采用自适应小波包变换方法选取最佳小波包分解尺度。首先，对声波信号采用小波包进行2—6尺度分解，分别计算各尺度下小波包系数的数学期望，并作为阈值进行置零处理，再计算置零处理后小波包系数的稀疏度，选取稀疏度最高的尺度作为小波包分解的最佳分解尺度，从而完成锅炉炉管声波信号的自适应小波包变换。

2.4 小波包系数块分类

为进一步提高本文算法在锅炉炉管声波报警系统中的应用性能，声波信号经小波包自适应变换后，重新计算最高分解尺度下各小波包系数块的数学期望和信息熵[24]，并基于数学期望和信息熵对各小波包系数块进行分类。

1）低频系数块 声波信号在小波包变换的最高分解尺度下的低频系数块包含信号的最主要特征，为非稀疏信号。对此部分信号进行压缩感知，不但会增加算法的处理时间，而且会降低信号的重构精度。所以，低频系数块不需要进行处理，直接进行传输即可。

2）无效系数块 系数块数学期望为0时，说明该系数块中所有值均为0。该系数块在压缩、传输、存储中均无利用价值，可以不用考虑。所以，无效系数块不需要参于数据处理、传输与存储等运算。

3）特殊系数块 系数块的数学期望不为0而信息熵为0，或者系数块的数学期望小于特定值时，系数块属于特殊类型。根据系数块信息熵概念[25]，当系数块的数学期望不为0而信息熵为0时，说明系数块中只包含1个非零项系数。对特殊系数块，也不需要进行数据处理，只需对非零项的大小和位置进行编码，然后传输。

4）压缩感知系数块 系数块的数学期望和信息熵均不为0，说明系数块中不为0的系数项较多，对该系数块采用压缩感知算法进行处理比较合理。

2.5 信号重构

信号重构包括小波包系数块重构和小波包重构两部分。在信号接收端，小波包系数块重构包括4个部分：1）低频系数块放置在小波包系数的低频部分；2）特殊系数块根据系数的非零值大小和位置进行解码，其他位置补零；3）压缩感知系数块采用OMP算法重构[26-27]系数块，并放置在相应位置；4）小波包的其他位置均用0进行补充。完成小波包系数块重构后，对小波包系数进行逆变换，完成信号的小波包重构。

根据上述分析，锅炉炉管声波信号的压缩感知与信号重构流程如图1所示。

图1 锅炉炉管声波信号的压缩感知与重构流程

3 实验与分析

实验过程中，采用信号压缩比（compression ratio，CR）来评价算法对声波信号的压缩效果[28]，压缩比的计算公式为

式中、分别表示信号压缩前、后的数据量。

采用峰值信噪比（peak signal to noise ratio，PSNR）[29]评价算法对声波信号的重构精度，PSNR的计算公式为

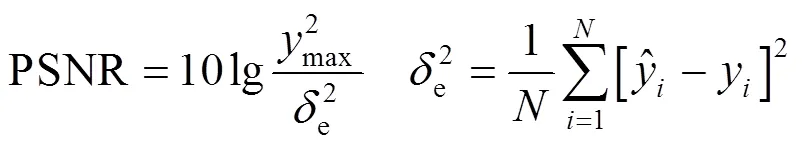
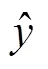
通过实验可知，当声波信号重构后的PSNR值大于40 dB时，重构后的信号才能完整地反映原始声波信号的所有信号特征。

3.1 数学期望作为小波包系数阈值的合理性验证

从历史数据中任意截取5段长度为256个采样点的声波信号，采用Sym5小波基对信号进行4尺度小波包分解，并计算各信号4尺度下小波包系数高频部分的数学期望。分别以1.2倍、1.0倍、0.8倍数学期望（1.2、1.0、0.8）为阈值对4尺度下小波包系数进行置零处理。然后按本文小波包系数块分类方法对各信号进行重构，分别计算各声波信号的CR/PSNR值（表3）。由表3可见：小波包系数的置零阈值越大，其数据压缩率越高，这是因为置零阈值越大，则小波包系数的稀疏度越高，则压缩率越高；当采用1.2作为小波包系数阈值时，其信号的重构精度低于1.0，这是因为前者的阈值较大，采用过大阈值对小波包系数进行置零处理会丢失部分有用的信号特征，因而其重构精度不高；当采用1.0作为小波包系数阈值时，其信号的重构精度优于0.8，这是因为前者的阈值较大，采用较大阈值对小波包系数进行置零处理时，其信号的稀疏度高于后者，因而重构精度较高。综上所述，采用1.0作为小波包系数阈值时，信号的压缩率和重构精度均比较理想。

表3 不同阈值下的信号压缩率和重构精度

Tab.3 The signal compression and reconstruction accuracy under different thresholds

3.2 信号的自适应性比较

选取5段声波信号采用Sym5小波基对信号进行2—6尺度分解，分别计算各尺度下小波包系数的数学期望，将其作为阈值进行置零处理，再计算置零处理后小波包系数的稀疏度，选取稀疏度最高的尺度作为小波包分解的最佳分解尺度，然后比较信号的重构性能，信号的自适应性比较见表4。由表4可以看出，采用自适应小波包变换选取最佳小波包分解尺度方法处理信号时，信号1在第5尺度、信号2和信号5在第4尺度、信号3和信号4在第3尺度下均具有最高稀疏度，说明本文方法具有较好的自适应性。在各最佳分解尺度下采用数学期望作为小波包系数的置零阈值，其采样值比最高为54.34%，其重构误差完全满足信号处理要求。与表3进行比较，信号1、信号3、信号4由于选择了最佳分解尺度，其稀疏度和重构精度均得到提高。

表4 信号的自适应性比较

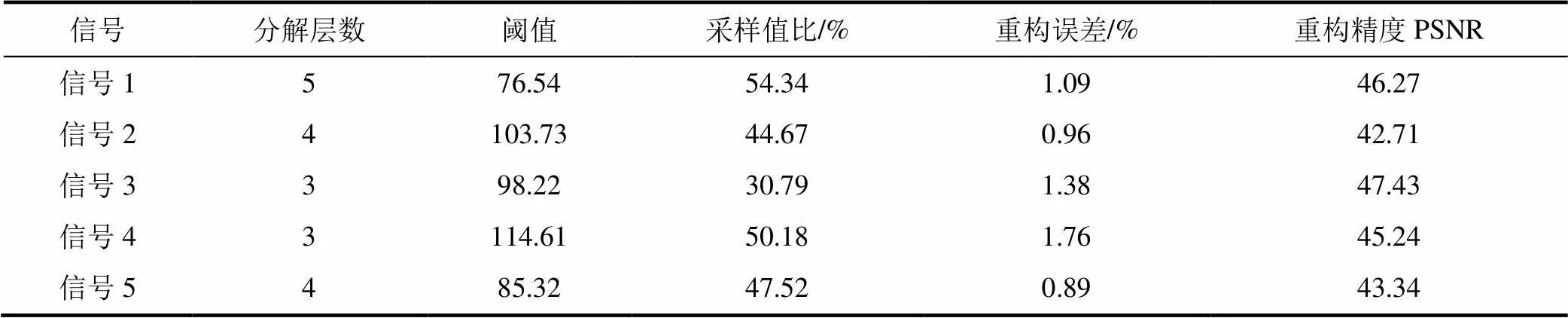
Tab.4 The adaptability of the signals

3.3 数据存储空间比较

对信号进行压缩感知时，其所需的存储空间主要由最大观测矩阵的大小来决定，当采用相同的观察次数时，其观测矩阵的大小相同。长度为256个采样点的信号在不同观察次数分别采用小波包算法和本文算法对信号进行稀疏变换，其最大观测矩阵的大小对比见表5。由于本文算法采用小波包系数块分开压缩的方法，其最大观测矩阵比小波包算法小很多。因此，本文算法所需的存储空间远小于小波包算法。

表5 信号观测矩阵大小对比

Tab.5 Comparison of the signal observation matrix size

3.4 信号重构效果比较

从历史数据中任意截取长度为256个采样点的声波信号，选择Sym5小波基，分别采用小波变换和小波包变换对信号进行4尺度分解，并将其数学期望作为阈值对系数进行置零处理，再采用本文算法对同段信号进行稀疏变换。在保证3种算法具有相同观察次数的条件下，分别对信号进行重构，不同算法的信号重构效果如图2所示。从图2可以看出，3种算法在相同的观察次数下，小波变换方法的信号重构效果最差；而小波包算法和本文算法的重构效果相差不大，但将波形放大后进行比较，可以看出本文算法的重构效果优于小波包算法。

图2 不同算法的信号重构效果

3.5 本文算法综合性能验证

从历史数据中不放回的随机截取1 500段长度为256个采样点的声波数据，分别采用Sym5小波基对信号进行4尺度小波分解、4尺度小波包分解，再分别计算4尺度下小波系数、小波包系数高频部分的数学期望，将其作为阈值对该尺度下的小波系数、小波包系数进行置零处理，然后采用信号压缩感知和正交匹配追踪方法完成信号重构；再采用本文算法对这1 500段声波进行信号处理和重构；分别计算3种算法下信号的平均压缩率、信号的平均重构精度以及信号的总处理时间，不同算法的性能比较见表6。由表6可知，本文算法在压缩率、重构精度以及运行时间上均优于其他2种算法。

表6 不同算法的性能比较

Tab.6 Performance comparison between different algorithms

4 结 论

1）与小波变换相比，小波包对声波信号的分解更为精细，提高了信号在频域的稀疏度，从而提高了信号的压缩率和重构精度。

2）采用不同尺度下的小波包系数高频部分的数学期望作为阈值对小波包系数进行置零处理，并基于各尺度下小波包系数的稀疏度自适应选择最佳小波包分解尺度，进一步提高了信号在频域的稀疏度，以及信号的压缩率和重构精度。

3）基于小波包各系数块的数学期望和信息熵对系数块进行分类，对不同类型的系数块采用不同的处理方法，有效降低了信号的传输带宽和存储容量，提高了信号的处理速度。

［1］ 何俊松. 炉管泄漏自动报警装置的技术改造[J]. 广西电力, 2018, 41(1): 63-66.HE Junsong. Technical modification of automatic warningsystem of boiler pipe leakage[J]. Guangxi Electric Power, 2018, 41(1): 63-66.

［2］ 陈捷, 陆云. 2016年度上海并网发电厂发电锅炉“四管”泄漏统计及案例分析[J]. 电力与能源, 2017, 38(2): 170-175. CHEN Jie, LU Yun. Statistics and case analysis of Shanghai Grid plant power boiler four-tube leakages in 2016[J]. Power and Energy, 2017, 38(2): 170-175.

［3］ ZHANG Z, RAO B D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 912-926.

［4］ DAVENPORT M A, WAKIN M B. Analysis of orthogonal matching pursuit using the restricted isometry property[J]. IEEE Transactions on Information Theory, 2011, 56(9): 4395-4401.

［5］ 强策, 夏凌, 李光瑞. 语音信号压缩感知观测矩阵的对比研究[J]. 西华大学学报(自然科学版), 2017, 36(2): 24-27. QIANG Ce, XIA Ling, LI Guangrui. A comparative study on observation matrix of compressed speech signal[J]. Journal of Xihua University (Natural Science), 2017, 36(2): 24-27.

［6］ 杨震, 徐珑婷. 语音信号处理中鲁棒性压缩感知关键技术[J]. 数据采集与处理, 2017, 32(2): 232-245. YANG Zhen, XU Longting. Key issues of robust compressed sensing in speech signal processing[J]. Journal of Data Acquisition and Processing, 2017, 32(2): 232-245.

［7］ 杜佳梦, 陈仪, 荣泽成. 浅述基于压缩感知的语音流媒体信号的丢包恢复[J]. 现代信息科技, 2018, 2(6): 67-68. DU Jiameng, CHEN Yi, RONG Zecheng. Packet loss recovery of speech streaming signals based on compressed sensing[J]. Modern Information Technology, 2018, 2(6): 67-68.

［8］ 贾晓立, 江晓波, 蒋三新, 等. 利用结构特征的语音压缩感知重建算法[J]. 上海交通大学学报, 2017, 51(9): 1111-1116. JIA Xiaoli, JIANG Xiaobo, JIANG Sanxin, et al. A reconstruction algorithm for speech compressive sensing using structural features[J]. Journal of Shanghai Jiao Tong University, 2017, 51(9): 1111-1116.

［9］ 陈益, 李文钧. 基于正交匹配追踪算法的语音信号重构研究[J]. 电子科技, 2018, 31(3): 44-47. CHEN Yi, LI Wenjun. Research on speech signal reconstruction based on orthogonal matching pursuit algorithm[J]. Electronic Science and Technology, 2018, 31(3): 44-47.

［10］ 隋昊, 周萍, 沈昊, 等. 基于混沌序列的压缩感知语音增强算法[J]. 微电子学与计算机, 2018, 35(1): 96-99. SUI Hao, ZHOU Ping, SHEN Hao, et al. Compressed sensing speech enhancement algorithm based on chaotic sequences[J]. Microelectronics & Computer, 2018, 35(1): 96-99.

［11］ 赵煦, 刘晓航, 孟永鹏, 等. 采用小波包树能量矩阵奇异值分解的局部放电模式识别[J]. 西安交通大学学报, 2017, 51(8): 116-121. ZHAO Xu, LIU Xiaohang, MENG Yongpeng, et al. Partial discharge pattern classification by singular value decomposition of wavelet packet energy features[J]. Journal of Xi’an Jiaotong University, 2017, 51(8): 116-121.

［12］ 张然然, 刘鑫屏. 火电机组超短期负荷预测[J]. 热力发电, 2018, 47(7): 52-57. ZHANG Ranran, LIU Xinping. Ultra-short-term load forecasting for thermal power units[J]. Thermal Power Generation, 2018, 47(7): 52-57.

［13］ 高翔, 牟法海, 卢盛阳, 等. 基于小波变换的汽轮发电机组动静碰摩特征分析[J]. 热力发电, 2011, 40(8): 17-21.GAO Xiang, MU Fahai, LU Shengyang, et al. Characteristicanalysis of impact-rubbing between movable and stationaryparts on turbo-generator set[J]. Thermal Power Generation, 2011, 40(8): 17-21.

［14］ 李培生, 孙金丛, 李伟. 生物质微商热重数据不同去噪方法分析[J]. 热力发电, 2017, 46(1): 62-67. LI Peisheng, SUN Jincong, LI Wei. Different de-noised methods for derivative thermogravimetry data of biomass[J]. Thermal Power Generation, 2017, 46(1): 62-67.

［15］ HUANG S J, CHEN S G. A high-throughput radix-16 FFT processor with parallel and normal input-output ordering for IEEE 802.15.3c systems[J]. IEEE Transactions on Circuits & Systems I Regular Papers, 2012, 59(8): 1752-1765.

［16］ WAGNER N, ELDAR Y C, FRIEDMAN Z. Compressed beamforming in ultrasound imaging[J]. IEEE Transactions on Signal Processing, 2012, 60(9): 4643-4657.

［17］ LUSTIG M, DONOHO D L, SANTOS J M, et al. Compressed sensing MRI[J]. IEEE Signal Processing Magazine, 2008, 25(2): 72-82.

［18］ ZHONG S, WEI Q, HUANG X. Compressive sensing beamforming based on covariance for acoustic imaging with noisy measurements[J]. The Journal of the Acoustical Society of America, 2013, 134(5): EL445-EL451.

［19］ NING F L, LIU Y, ZHANG C, et al. Acoustic imaging with compressed sensing and microphone arrays[J]. Journal of Computational Acoustics, 2017, 25(4): 1750027.

［20］ CHU N, PICHERAL J, MOHAMMAD-DJAFARI A, et al. A robust super-resolution approach with sparsity constraint in acoustic imaging[J]. Applied Acoustics, 2014, 76: 197-208.

［21］罗孟儒, 周四望. 自适应小波包图像压缩感知方法[J]. 电子与信息学报, 2013, 35(10): 2371-2377. LUO Mengru, ZHOU Siwang. Adaptive wavelet packet image compressed sensing[J]. Journal of Electronics & Information Technology, 2013, 35(10): 2371-2377.

［22］ 刘焕淋, 王储君, 陈勇. 基于分段自适应采样压缩感知的FBG光谱压缩与重构方法[J]. 中国激光, 2018, 45(3): 1-8. LIU Huanlin, WANG Chujun, CHEN Yong. FBG spectral compression and reconstruction method based on segmented adaptive sampling compressed sensing[J]. Chinese Journal of Lasers, 2018, 45(3): 1-8.

［23］ 高悦, 臧明相, 郭馥英. 基于小波变换和压缩感知的语音信号压缩研究[J]. 计算机应用研究, 2017, 34(12): 3672-3680. GAO Yue, ZANG Mingxiang, GUO Fuying. Research on speech compression based on wavelet transform and compressed sensing application[J]. Research of Computers, 2017, 34(12): 3672-3680.

［24］ 吴建萍, 姜斌, 刘剑慰. 基于小波包信息熵和小波神经网络的异步电机故障诊断[J]. 山东大学学报(工学版), 2017, 47(5): 223-228. WU Jianping, JIANG Bin, LIU Jianwei. Fault diagnosis of asynchronous motor based on wavelet packet entropy and wavelet neural network[J]. Journal of Shandong University (Engineering Science), 2017, 47(5): 223-228.

［25］ 黎威, 张健.基于小波包的相位敏感OTDR分布式光纤振动信号降噪方法的研究[J]. 光电子·激光, 2017, 28(1): 32-37. LI Wei, ZHANG Jian. Wavelet packet denoising method in phase-sensitive OTDR distributed vibration sensor[J]. Journal of Optoelectronics·Laser, 2017, 28(1): 32-37.

［26］ 丁续达, 刘潇, 金秀章. 基于压缩感知最小二乘支持向量机的NO软测量模型[J]. 热力发电, 2018, 47(3): 76-81. DING Xuda, LIU Xiao, JIN Xiuzhang. A soft sensor model for NOconcentration based on CS-LSSVM[J]. Thermal Power Generation, 2018, 47(3): 76-81.

［27］ 赵小虎, 刘闪闪, 沈雪茹, 等. 基于分布式压缩感知的微震数据压缩与重构[J]. 中国矿业大学学报, 2018, 47(1): 172-182. ZHAO Xiaohu, LIU Shanshan, SHEN Xueru, et al. Micro-seismic data compression and reconstruction based on distributed compressed sensing[J]. Journal of China University of Mining & Technology, 2018, 47(1): 172-182.

［28］ 袁莉芬, 孙业胜, 何怡刚, 等. 基于小波包优选的模拟电路故障特征提取方法[J]. 电工技术学报, 2018, 33(1): 158-165. YUAN Lifen, SUN Yesheng, HE Yigang, et al. Fault feature extraction method for analog circuit based on preferred wavelet packet[J]. Transactions of China Electro-Technical Society, 2018, 33(1): 158-165.

［29］ 许华杰, 何敬禄, 胡小明. 基于块稀疏度估计的压缩感知自适应重构算法[J]. 计算机应用研究, 2018, 35(1): 305-308. XU Huajie, HE Jinglu, HU Xiaoming. Adaptive reconstruction algorithm based on estimating of block sparsity in compressed sensing[J]. Application Research of Computers, 2018, 35(1): 305-308.

Adaptive compressed sensing of boiler tube acoustic signals based on wavelet packet

YANG Zhengli, SHI Wen, CHEN Haixia

(School of Mechanical and Electrical Engineering, Sanjiang University, Nanjing 210012, China)

In the automatic alarm system for leakage of boiler tubes based on acoustic signals, to solve the problems of large data size, high transmission bandwidth and large storage occurred during the acquisition, transmission, processing and storage of acoustic signals, an adaptive compressed sensing method for the boiler tube acoustic signals based on wavelet packet is proposed. Firstly, the wavelet packet analysis method is used to decompose the acoustic signals of the boiler tube in multiple scales, and the mathematical expectation of the wavelet packet coefficient under each scale is calculated as the threshold value. The wavelet packet coefficient is zero processed, and the optimal wavelet packet decomposition layer number is selected adaptively according to the sparse degree values under each decomposition scale. Then, each wavelet packet coefficient block under the optimal decomposition layer is classified according to its mathematical expectation and information entropy, and each wavelet packet coefficient block after classification is processed by different methods. The method in this paper is applied to the historical data of the acoustic wave automatic alarm system of a boiler tube, the results show that, the proposed method can effectively reduce the observed data of acoustic signals in furnace tubes, increase the signal compression rate, reduce the transmission bandwidth and storage capacity of signals at the same observation times, and improve the processing speed and reconstruction accuracy of signals.

boiler, boiler tube, acoustic signal, signal compression, wavelet packet analysis, compressed sensing, mathematical expectation

TP391; TN912.3; TM621.2

A

10.19666/j.rlfd.201810207

杨正理, 史文, 陈海霞. 基于小波包的锅炉炉管声波信号自适应压缩感知[J]. 热力发电, 2019, 48(5): 114-120. YANG Zhengli, SHI Wen, CHEN Haixia. Adaptive compressed sensing of boiler tube acoustic signals based on wavelet packet[J]. Thermal Power Generation, 2019, 48(5): 114-120.

2018-10-25

江苏省高校自然科学研究面上项目(17KJB470011)

Project of Natural Science Research in Universities of Jiangsu Province (17KJB470011)

杨正理(1971—)，男，硕士，副教授，主要研究方向为复杂系统与计算智能技术，zhengli-yang@163.com。

（责任编辑 杜亚勤）