套筒约束灌浆料与钢筋黏结强度试验研究
2020-10-11黄远张帆易伟建1
黄远,张帆,易伟建1,
(1.湖南大学工程结构损伤诊断湖南省重点实验室,湖南长沙 410082;2.湖南大学 土木工程学院,湖南 长沙 410082)
钢筋套筒灌浆连接是指在预制构件中预埋套筒,再插入钢筋并灌注浆料而实现钢筋的对接连接,是目前我国装配式混凝土结构受力钢筋连接的主要形式[1-2].
目前,国外学者对不同形式的套筒进行了拉拔性能研究.Ling 等[3]设计制作了钢筋焊接套筒(THS)和锥形套筒(WBS);Hosseini 等[4]、Alias 等[5]设计的焊螺旋钢筋式套筒;Henin 等[6]设计的内螺纹套筒、端部焊钢板式套筒;Seo 等[7]设计的钢筋带端头式套筒.通过改变套筒构造等措施,有效地增加了钢筋与灌浆料之间的黏结性能,避免试件发生钢筋拔出破坏.
国内学者也对钢筋套筒灌浆连接接头的性能进行了研究.郑永峰等[8]设计制作了变形灌浆套筒(GDPS),研究了套筒内腔构造对黏结性能的影响,结果表明:在套筒两端增设肋纹,可有效避免发生套筒灌浆料黏结破坏,当肋纹出现在非弹性段时,减小了钢筋与灌浆料之间的平均黏结强度;黄远等[9]设计了14 个钢筋半套筒灌浆连接试件进行拉伸试验,研究钢筋直径、钢筋偏移对接头性能的影响,结果表明:钢筋偏移对试件承载力的影响可忽略不计;吴小宝等[10]研究了灌浆料养护龄期和钢筋类别对钢筋套筒灌浆连接性能的影响,结果表明:龄期1 天以后,荷载位移曲线出现明显的屈服和强化阶段;许成顺等[11]研究了钢筋套筒灌浆连接接头在高应力反复拉压荷载作用下的接头性能,结果表明:高应力反复拉压对端部灌浆料造成一定的损伤,但对连接试件的性能无明显影响.
目前国内外套筒灌浆连接接头性能研究主要关注套筒形式的合理性论证,对于套筒中灌浆料和钢筋的黏结性能的研究较少.因此,本文设计了30 个钢筋与套筒约束灌浆料连接试件进行拉拔试验,研究钢筋锚固长度、灌浆料抗压强度、灌浆料厚度和钢筋直径四个参数对黏结强度的影响.并根据Einea等[12]提出套筒与灌浆料隔离体约束应力分析模型来分析钢筋与套筒约束灌浆料试件的黏结强度.
1 试验概况
1.1 试件设计
为了研究套筒中钢筋与灌浆料的黏结性能,设计了10 组,每组3 个共30 个试件.研究的主要参数包括钢筋锚固长度、灌浆料强度、灌浆料厚度及钢筋直径,试件的参数取值如表1 所示.以标准试件L16-0.14-D16-4d 为例,第一组表示套筒规格,表示不同钢筋直径(12 mm、16 mm、20 mm)所对应的套筒规格;第二组表示灌浆料的水料比(0.14、0.15、0.16);第三组表示连接钢筋的直径d0(12 mm、16 mm、20 mm);第四组表示锚固长度(3 d0、4 d0、5 d0).套筒连接中的灌浆料厚度g 用公式(1)计算.

式中:g 表示灌浆料厚度(mm);D 表示套筒外径(mm);d0表示钢筋直径(mm);t 表示套筒壁厚(mm).各符号的含义见图1.

表1 试件参数Tab.1 Parameters of specimens
试件制作时,把全灌浆套筒沿横向中间位置切割成两个大小相等的半套筒,为了保证黏结长度,沿钢筋长度方向设置了无黏结段,无黏结段通过PVC管来隔离钢筋与灌浆料之间的黏结,PVC 管缝隙塞入工业橡皮泥以防止漏浆.钢筋处于套筒中心位置,无偏心.加载端钢筋伸出400 mm,自由端钢筋伸出60 mm,如图1 所示.

图1 试件尺寸和符号Fig.1 Dimension of specimen
1.2 材料性能
试验中连接钢筋采用HRB500 月牙形带肋钢筋,其力学性能如表2 所示.
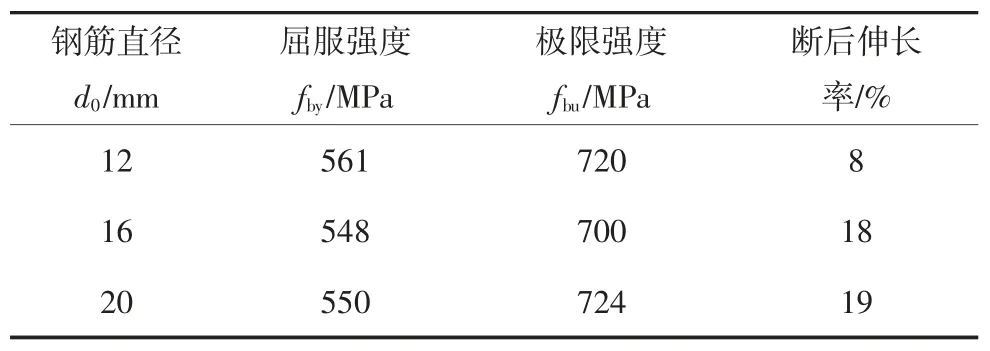
表2 钢筋材料性能Tab.2 Material properties of reinforcement bar
试验中灌浆料采用西卡(中国)有限公司生产的Sika-Grout PC 牌灌浆料.根据GB/T 17671—1999《水泥胶砂强度检验方法(ISO 法)》,测得其40 mm×40 mm×160 mm 灌浆料试块抗压强度如表3 所示.套筒采用挤压成型钢套筒,其弹性模量Esl=2.06 ×105MPa.

表3 灌浆料材料性能Tab.3 Material properties of grout
1.3 试验装置及测量布置
试验加载装置如图2 所示,采用HC-20 型锚杆拉拔仪进行加载.数显千分表竖直放置于钢筋自由端部,用以量测拉拔过程中钢筋的滑移.拉拔荷载40 kN 之前,加载按力控制,以荷载2 kN 为增量进行读数,荷载超过40 kN 以钢筋滑移量每10 μm 为增量进行位移控制读数,以捕获极限荷载.当拉拔荷载出现明显下降后,以每500 μm 滑移为增量进行读数,钢筋滑移量达到20 mm 时停止加载.
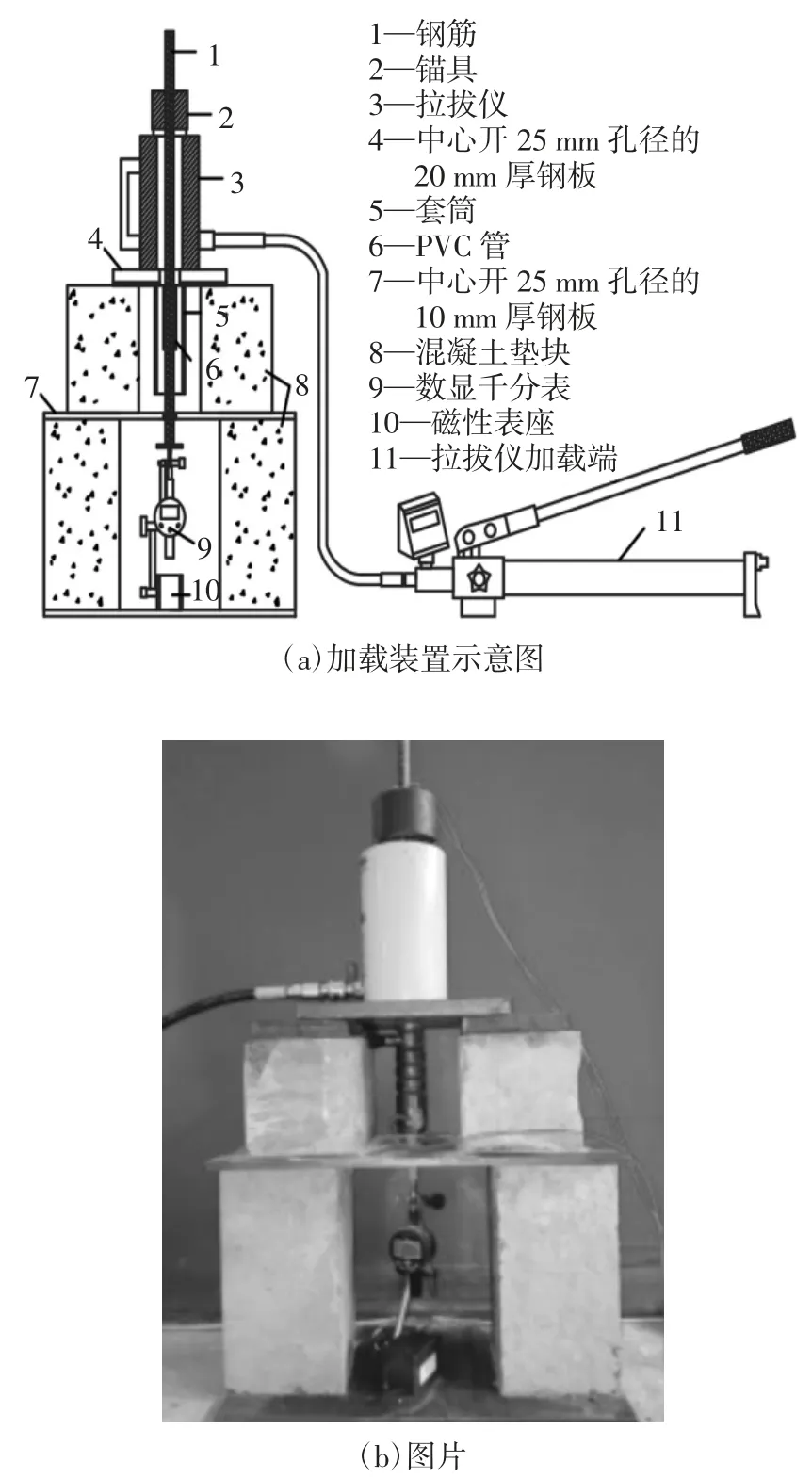
图2 试验装置Fig.2 Test setup
每个试件上设置两个应变片如图3 所示.S1 沿套筒横向安装在距离套筒自由端L0/3 黏结段位置处,用以测量套筒由于灌浆料膨胀引起的环向应变;S2 沿加载端钢筋纵向安装在距离套筒承压段一倍钢筋直径位置处,用以测量拉拔试验过程中钢筋的纵向应变.

图3 应变片布置Fig.3 Strain gauges
2 试验结果
各个试件的试验结果如表4 所示.εsl表示试件达到最大承载力时对应的套筒环向应变(mm/mm).钢筋黏结强度τu按公式(2)计算.

表4 试验结果Tab.4 Test results of specimens

式中:τu表示钢筋黏结强度(MPa),Pu表示试件最大承载力(kN),d0表示钢筋直径(mm),L0表示钢筋锚固长度(mm).
试件的破坏模式为两种:
1)钢筋拔出破坏,如图4(a)所示:试件加载初期黏结-滑移曲线表现出良好的弹性响应,同时试件内灌浆料沿钢筋肋纹表面产生微裂纹并逐渐发展,试件刚度逐渐降低;随着钢筋屈服,钢筋明显伸长,表现在上部钢筋锚具发生明显位移,下部千分表示数基本不变,拉拔仪荷载上下波动;钢筋屈服后,试件处于强化阶段,荷载、滑移持续增加,达到试件最大承载力后,荷载逐渐下降,钢筋的滑移量明显增加,加载到20 mm 时,停止加载,如图5 所示.

图4 试件破坏形态Fig.4 Specimen failure patterns
2)钢筋拉断破坏,如图4(b)所示:只有试件L16-0.14-D16-5d-2 发生这种破坏.钢筋拉断发生在试件达到最大承载力后荷载下降段,断裂位置处于距离套筒端部20 mm 位置,有明显的颈缩现象.试件最大承载力133.03 kN.
套筒环向应变随着荷载的变化曲线如图6 所示.在拉拔荷载初期,套筒环向呈现线性拉伸应变,当荷载达到峰值强度后,套筒环向应变随着荷载的增加而迅速增大,说明此时套筒对灌浆料产生了约束作用.
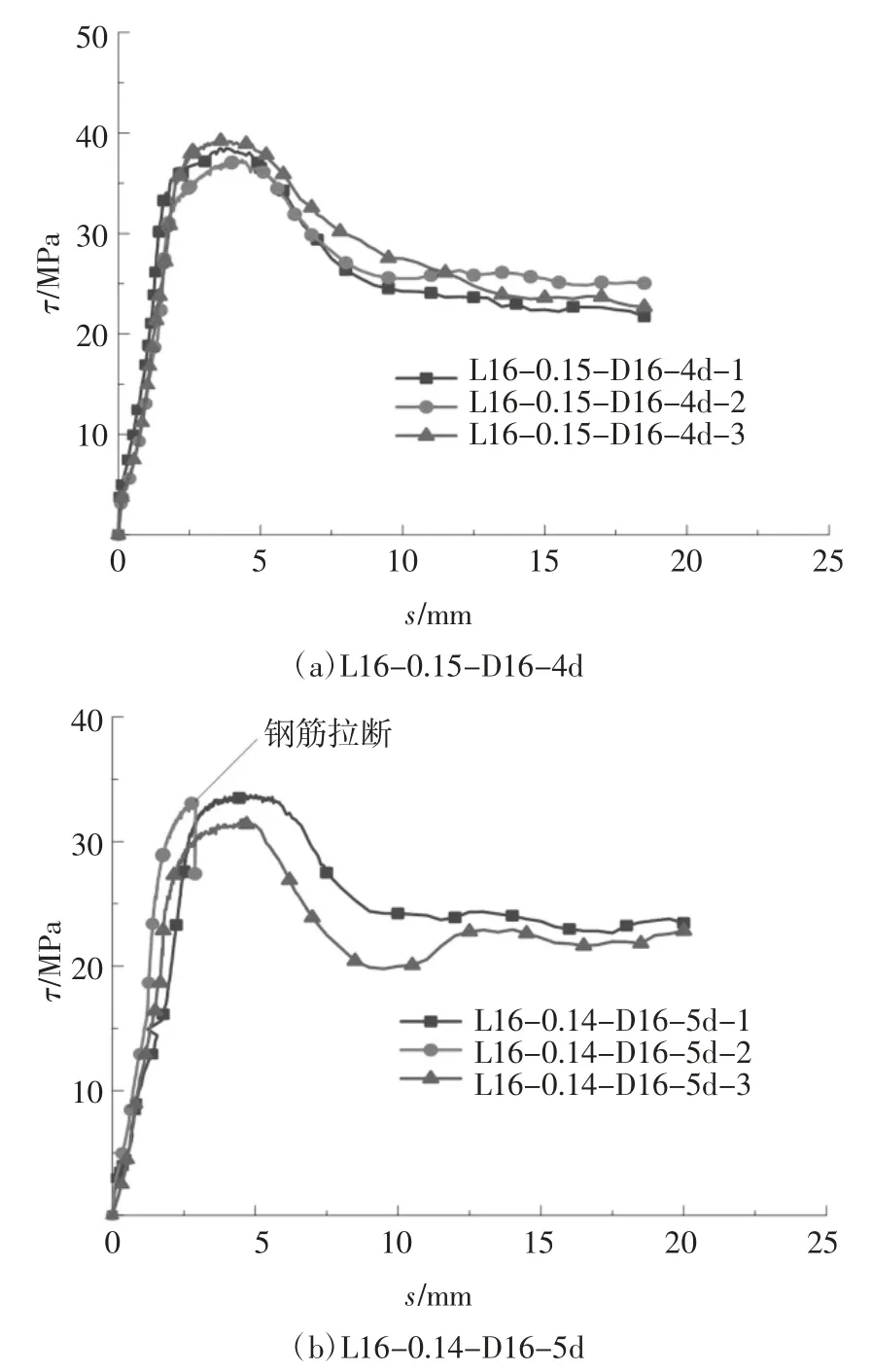
图5 试件典型黏结-滑移曲线Fig.5 Specimen bond stress-slip curves

图6 套筒环向应变Fig.6 Transverse strain responses of sleeve
3 试验结果分析
3.1 钢筋锚固长度
图7 为16 mm 直径钢筋的黏结强度在不同锚固长度下的变化情况.钢筋锚固长度从3d0增加到4d0,钢筋黏结强度平均值从44.68 MPa 降低到40.7 MPa,降低了8.9%,锚固长度从4d0增加到5d0,黏结强度平均值从40.7 MPa 降低到32.86 MPa,降低了19.3%.黏结强度随着锚固长度的增加而降低,这是由于黏结强度沿钢筋锚固长度范围内分布不均匀导致的,黏结强度在加载端附近存在一个峰值,锚固长度越大,其端部黏结强度峰值对平均黏结强度影响越小,因此黏结强度越小.
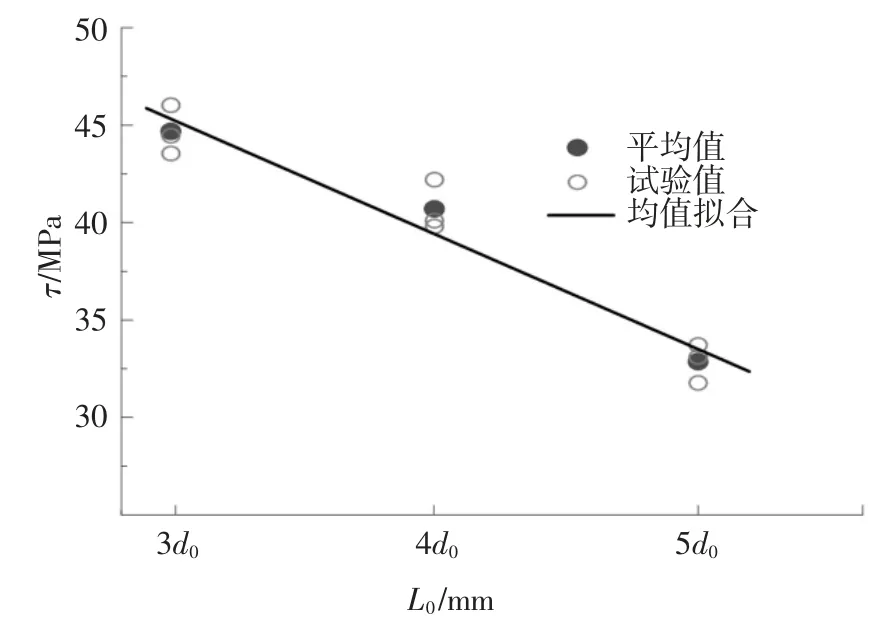
图7 锚固长度对黏结强度的影响Fig.7 Influence of anchorage length on bond strength
3.2 灌浆料抗压强度
图8 为钢筋黏结强度随灌浆料抗压强度变化的情况.抗压强度从61.5 MPa 增加到81.1 MPa,黏结强度平均值增加了8.2%,抗压强度从81.1 MPa 增加到92.5 MPa 时,黏结强度平均值增加了6.2%.黏结强度随着抗压强度的增加而增加,这是因为试件均为钢筋拔出破坏,其承载力取决于钢筋与灌浆料的机械咬合区域的抗剪强度,而灌浆料抗压强度增加,增强了灌浆料的抗剪强度,黏结强度增加.

图8 灌浆料抗压强度对黏结强度的影响Fig.8 Influence of grouting compressive strength on bond strength
3.3 灌浆料厚度
试验通过保持钢筋直径不变,改变套筒规格的方式改变套筒与钢筋之间的灌浆料厚度,研究灌浆料厚度对钢筋黏结性能的影响.图9 为直径12 mm的钢筋黏结强度随灌浆料厚度变化的情况.灌浆料厚度由9.5 mm 增加到11.2 mm,由11.2 mm 增加到12.3 mm,黏结强度平均值分别降低了1.0%和6.2%.
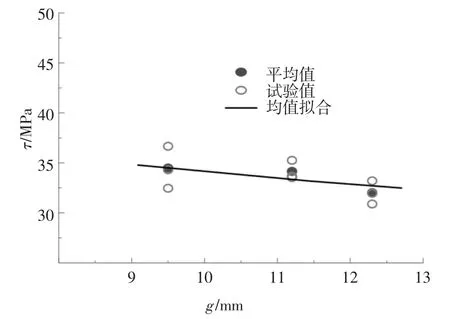
图9 灌浆料厚度对黏结强度的影响Fig.9 Influence of grout thickness on bond strength
3.4 钢筋直径
图10 给出了黏结强度随着钢筋直径变化的数据.钢筋直径从12 mm 增加到16 mm 时,黏结强度呈增大趋势,钢筋直径从16 mm 增加到20 mm 时,黏结强度又发生了减小.由于本次试验中黏结强度随着钢筋直径变化的规律不明显,因此钢筋直径对黏结强度影响还需要进一步的研究.
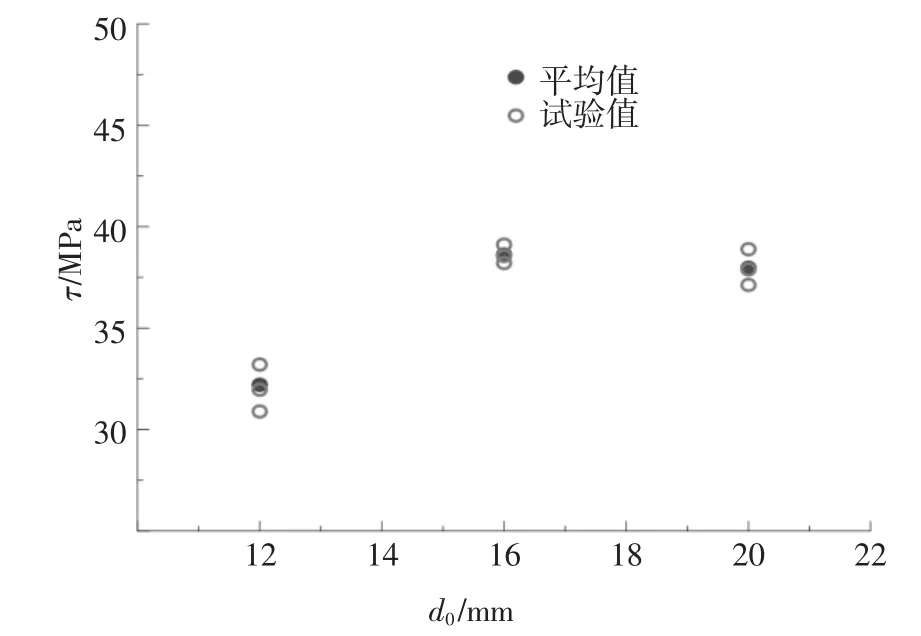
图10 钢筋直径对黏结强度的影响Fig.10 Influence of reinforcement diameter on bond strength
4 黏结强度理论分析
为了分析钢筋与灌浆料之间的黏结强度,采用Einea 等[12]提出的套筒与灌浆料隔离体约束应力分析模型来分析钢筋套筒约束灌浆料试件的黏结性能.如图11 所示,可以推导出了环向拉力Tsl与约束应力un的关系.
模型分析时基于以下4 个假定:
1)由套筒引起的约束应力沿钢筋锚固长度分布均匀;
2)约束应力可由套筒的环向应变量化得出;
3)黏结应力沿钢筋锚固长度范围内分布均匀;
4)由套筒引起的总约束力大小等于作用在钢筋上的总约束力.

图11 灌浆套筒约束应力模型Fig.11 Confined stress model of grouting sleeve
套筒的环向拉伸应力是套筒环向应变εsl和弹性模量Esl的函数,如式(3)所示.同时,拉伸应力也受套筒横截面积的影响,如式(4)所示.

式中:σsl表示套筒环向拉伸应力(MPa),εsl表示套筒环向应变(mm/mm),Esl表示套筒弹性模量(MPa);t表示套筒厚度(mm).
综合公式(3)、(4)可得:

根据静力平衡条件可得:

联立公式(5)、(6)得到:

式中:Tsl表示套筒环向拉力(N),un表示套筒提供的约束应力(MPa),D0表示套筒内径(mm).
Untrauer 和Henry[13]研究表明,钢筋与混凝土的黏结强度τu与钢筋上的约束应力un和灌浆料抗压强度fg成比例增加,其关系式为:
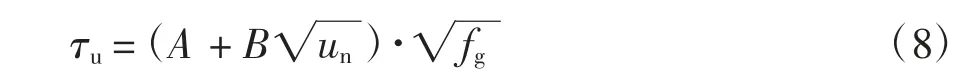
将式(7)代入式(8),可得:
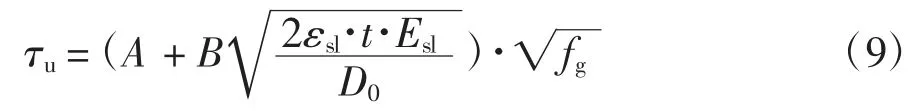
式中:A、B 通过实验数据回归拟合得到.将本文试验测试得到的套筒数据(表1)、灌浆料强度(表3)和黏结强度及对应的应变数据(表4)代入公式(9)进行回归分析,可以回归得到参数A 取为3.1,B 取为0.11.因此钢筋黏结强度的拟合公式如下:
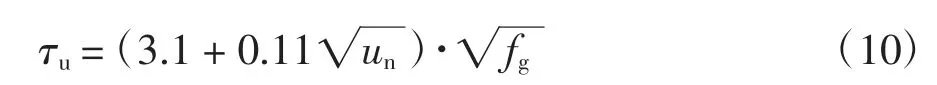
根据黏结强度τu可得钢筋套筒约束灌浆连接试件的最大承载力Pu计算式如下:

根据式(10)计算得到的各个试件的黏结强度代入式(11)可以得到各个试件的理论计算承载力Pu,pre,理论计算承载力Pu,pre和试验承载力Pu,exp对比如图12 所示.
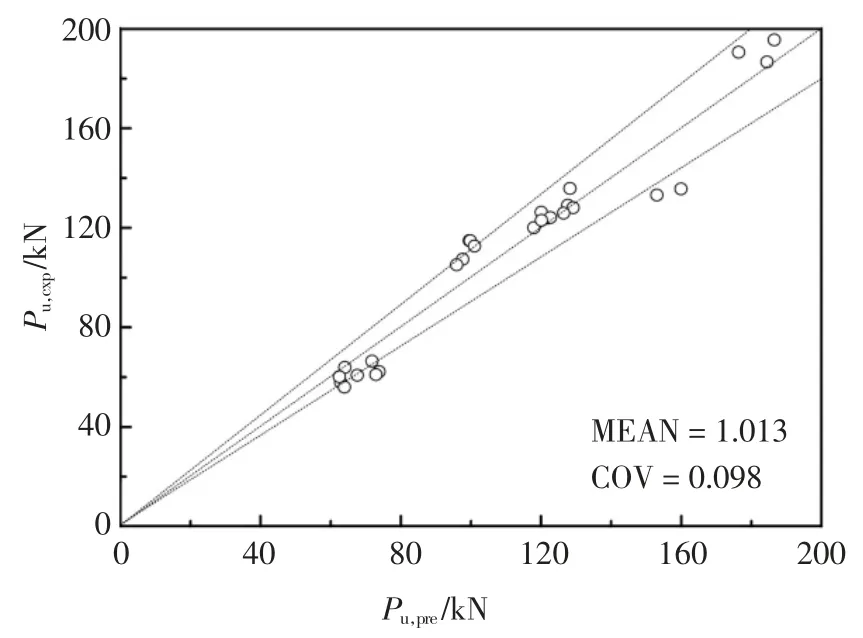
图12 简化公式结果与试验结果对比Fig.12 Comparison between predictions and test results
5 结论
通过套筒灌浆连接静力拉拔试验和分析,可以得到以下结论:
1)钢筋锚固长度增加,试件最大承载力增加;而随着锚固长度增加,导致钢筋上的黏结应力分布不均匀,黏结强度降低;
2)灌浆料抗压强度增加,增加了灌浆料抗剪强度,因此试件最大承载力和黏结强度均增加;
3)套筒内灌浆料厚度增加,钢筋与灌浆料的黏结强度减小,当灌浆料厚度超过11 mm 时,影响更大;
4)通过应力模型推导了黏结强度与约束应力、灌浆料抗压强度的关系式,可供工程实际中套筒灌浆连接节点锚固长度取值参考.
