考虑疲劳损伤的栓钉式组合梁剩余承载力计算方法

项贻强，何百达

（浙江大学 建筑工程学院，浙江 杭州 310058）

钢-混组合梁能够充分利用混凝土及钢梁材料性能，且其受力体系简便，施工工序简单，适用于城市快速施工等优势在我国的公路交通事业中得到广泛运用.目前，各国学者对组合梁的静力性能进行了大量研究，并已取得丰硕的成果，但在疲劳性能方面，其研究相对不足，仍缺乏能够准确描述组合梁的疲劳设计理论[1].

目前，在组合梁疲劳性能研究方面，主要从剪力连接件及整梁两方面进行展开.在栓钉连接件疲劳特性研究方面，王宇航等[2]基于断裂力学理论，建立了可用于预测栓钉连接件疲劳寿命的方法；荣学亮等[3]考虑了疲劳损伤，并基于大量试验数据的回归分析，提出了一种能够考虑栓钉初始缺陷的承载力退化方法，与试验结果验证良好；汪炳等[4]基于二元疲劳判据建立了栓钉承载力退化模型，并与所设计试验进行比对和有效验证.

在整梁疲劳特性方面，目前多集中于试验研究，并就影响整梁疲劳的几大关键因素进行讨论[5-7]；在理论研究方面，汪炳[8]提出了考虑各个构件疲劳退化的组合梁承载力理论方法的研究，与试验研究吻合良好，但该理论模型未考虑栓钉初始缺陷大小的影响；在有限元分析方面，主要通过考虑基于试验所得的S-N 分析曲线建立有限元模型[9-10]，并用试验值进行验证，但该方法的前提需要事先获得疲劳性能数据，且对不同材料、试验参数的组合梁的疲劳特性是否同样具有普遍适用性有待验证，因而具有一定的局限性.

基于以上研究背景，本文通过引入基于累计损伤的混凝土板、钢梁承载力退化模型及能够考虑初始缺陷的栓钉承载力退化模型，并通过对剩余组合梁承载力计算，建立能够研究组合梁在疲劳加载下的承载力变化的方法，进而对其关键影响因素进行分析，以期对工程设计提供理论支持.

1 理论模型

钢-混组合结构是由栓钉剪力连接件、钢主梁、混凝土板组成，其承载力也与三者紧密相关.在疲劳荷载作用下，各个构件以不同的退化规律发生了强度的衰减，以下分别引入承载力退化公式以描述其疲劳荷载下承载力变化规律，并基于此以求得组合梁疲劳剩余承载力.

1.1 栓钉承载力退化

关于栓钉连接件的承载力退化模型，根据荣学亮等[3]研究选取能够考虑初始缺陷的理论公式，如下：

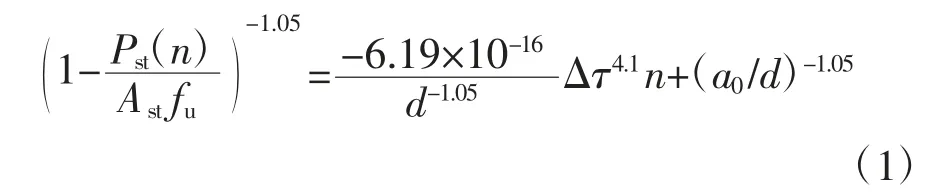
式中：d 为栓钉直径，Pst（n）为栓钉经n 次加载后的剩余强度，Ast为栓钉横截面面积，fu为栓钉所用钢材极限强度，Δτ 为疲劳剪应力幅，a0为初始裂缝长度，研究表明缺陷若为肉眼无法识别但已达到探伤Ⅱ级标准时可取2 mm[11]，该结论已得到有效运用[2-3]，故本文据此进行选取.

由式（1）可知，该式考虑了栓钉连接件的初始裂缝大小，其疲劳性能与自身材料参数及外界应力条件相关.在已知疲劳荷载及材料参数情况下便可求得其疲劳剩余承载力.

1.2 混凝土板承载力退化

关于混凝土板的承载力退化，可选取经典强度退化力学模型[12]，如下：

式中：fc（n）为混凝土疲劳剩余抗压强度，fc为混凝土初始抗压强度，σc，max为混凝土疲劳应力峰值，n 为疲劳加载次数，Nc为混凝土疲劳寿命，c1为混凝土材料参数，可由试验求得，若缺乏试验数据可选取为1.

由式（2）可知，为求混凝土的剩余承载力，需求得相应的混凝土疲劳寿命，在此选用经典Aas-Jakobsen 混凝土疲劳模型[13]：

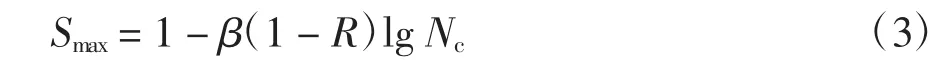
式中：Smax=为混凝土圆柱体抗压强度，R为疲劳应力比，即R=σc，min/σc，max，β 为与疲劳应力比相关的材料参数，文献[14]指出：当R≤0.8，对于轻骨料混凝土，β=0.069 4，对于普通凝土，则有β=0.067 9，为方便计算，可取平均值β=0.068 5，该疲劳模型已被工程界广泛采用.

1.3 钢梁承载力退化

在钢梁的疲劳承载力退化研究方面，前人已经进行了大量的研究，其疲劳力学模型一般选取为如下所示[15]：

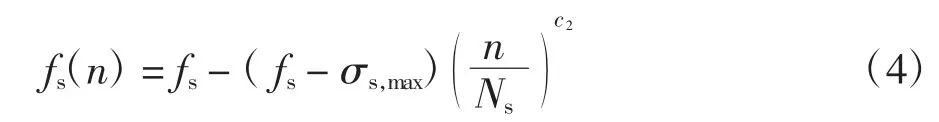
式中：fs（n）为钢梁疲劳剩余屈服强度，fs为钢梁初始屈服强度，σs，max为钢梁疲劳应力峰值，n 为疲劳加载次数，Ns为钢材疲劳寿命，c2为钢材材料参数，可由试验求得，若缺乏试验则可选取为1.

为求得钢梁的疲劳寿命，可参照《公路钢结构桥梁设计规范》（JTG D64—2015）[16]进行取值：

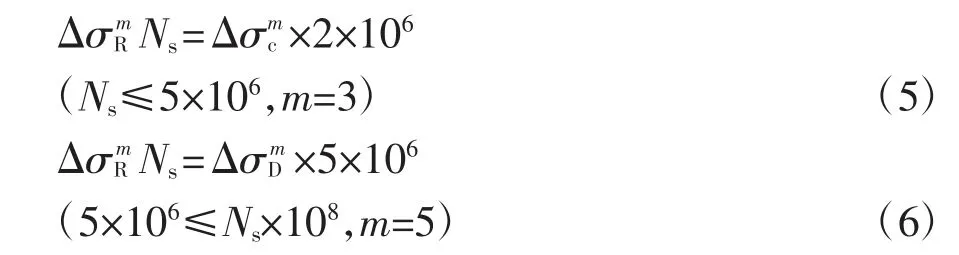
式中:Δσc是疲劳寿命为200 万次时对应的疲劳应力值，其值与疲劳细节相关，具体可参照规范JTG D64—2015 选取，ΔσD=0.737Δσc，ΔσR为疲劳强度，Ns为钢材疲劳寿命.

1.4 构件疲劳应力幅计算

关于各个构件的疲劳应力幅计算，考虑到实际工程中组合梁多为完全抗剪工作，且在正常使用荷载作用下滑移较小，因而可采用换算截面法进行简化计算.

于是，栓钉剪力连接件应力幅为：

式中：ΔV 为栓钉剪力幅，Sc为混凝土板对组合梁截面中心轴所取的面积矩，nh为栓钉横向布置数量，I 为组合梁的换算截面惯性矩，p 为栓钉纵向布置间距.

同理，钢梁和混凝土板的应力幅也可进行相应计算.

1.5 剩余承载力计算

组合梁在疲劳荷载作用下，钢梁、混凝土板、栓钉以不同程度各自发生微裂缝累积损伤，从而产生强度折减，并由初始完全抗剪结构逐渐转换为部分抗剪结构，因此需根据抗剪连接度的大小、中和轴位置分别进行考虑.在计算过程中，进行如下合理假设[8]：1）忽略混凝土板抗拉作用；2）考虑到实际情况下钢梁腹板、上翼缘板所受疲劳应力幅较小，因此为简化计算，仅考虑下翼缘板疲劳退化进行近似计算.

根据抗剪连接度定义，有：

式中：η（n）为经历n 次疲劳荷载后的剩余剪力连接度，ns为组合梁实际布置栓钉数量，nf为疲劳荷载后完全抗剪所需栓钉数量.若η（n）≤1，则按照非完全抗剪计算；若η（n）≥1，则按照完全抗剪计算.

1.5.1 部分抗剪组合梁承载力

组合梁在受到疲劳荷载后退化为非完全抗剪结构，该结构可根据不同塑性中和轴位置情况下的承载力进行计算[17]，如图1 所示.

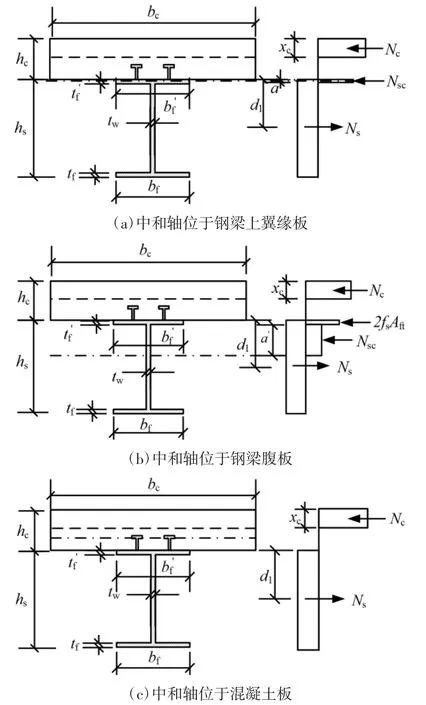
图1 部分抗剪组合梁承载力计算模型Fig.1 Calculation model of partial shear composite beam bearing capacity

1）塑性中和轴位于钢梁上翼缘板内

根据图中力的平衡则有：

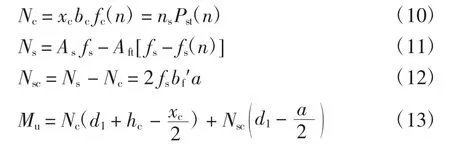
式中：Nc为考虑混凝土板衰减后合力，Ns为考虑钢梁下翼缘板强度衰减后合力，Nsc为2 倍上翼缘板受压区合力，xc为混凝土受压高度，a 为钢梁受压区高度，d1为考虑钢梁疲劳退化后的合力与上翼缘距离，As为钢梁截面积，Aft为下翼缘板截面积，bc为混凝土板宽度，hc为混凝土板高度，为钢梁上翼缘板宽度.

整理可得：

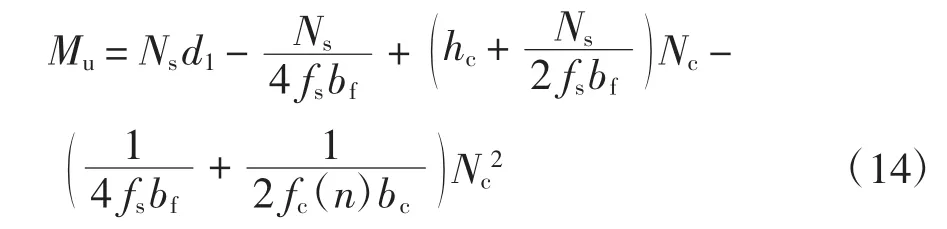
2）塑性中和轴位于钢梁腹板内

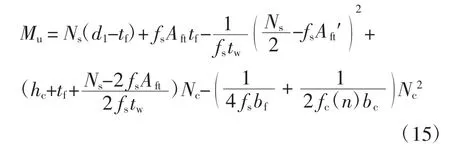
式中：tf为钢梁下翼缘板高度，tw为钢梁腹板宽度，bf为钢梁下翼缘板宽度，为上翼缘板截面积.

3）塑性中和轴位于混凝土板内

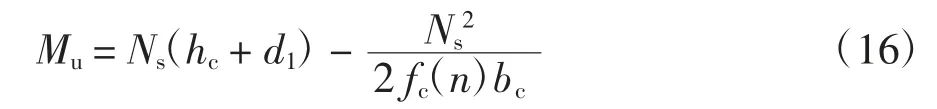
1.5.2 完全抗剪组合梁承载力

在加载初期，因疲劳裂缝开展较慢，损伤积累较小，其强度折减效应较小，仍可能为完全抗剪结构，因而可仍按完全抗剪计算.若塑性中和轴位于钢梁内，较于部分抗剪结构，完全抗剪结构极限承载力的计算模型表现在混凝土板为全截面受压[18]，即Nc=hcbcfc（n），从而可参照上述方法进行求解.

1）塑性中和轴位于钢梁上翼缘板内

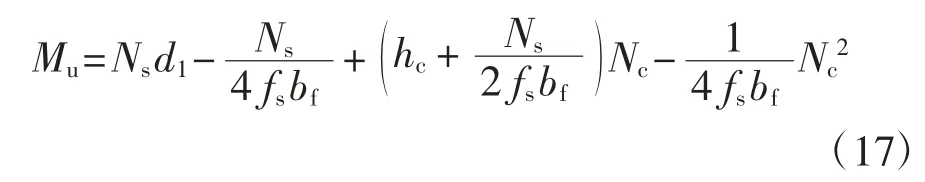
2）塑性中和轴位于钢梁腹板内

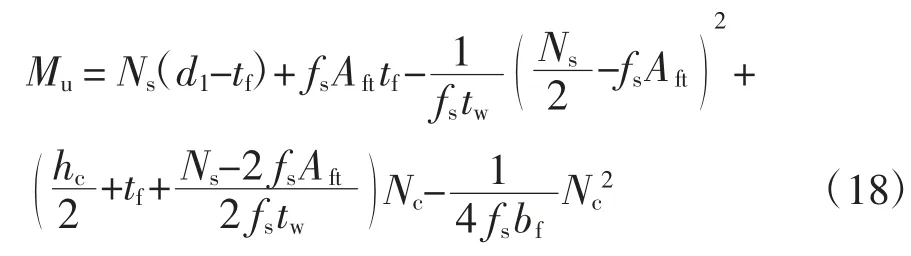
3）塑性中和轴位于混凝土板内

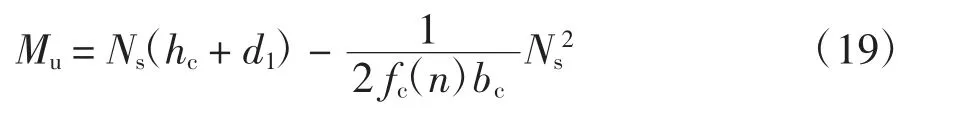
1.6 计算流程

基于上述分析，关于组合梁疲劳剩余承载力的计算流程如图2 所示.

图2 组合梁剩余承载力计算流程Fig.2 Composite beam residual bearing capacity calculation process

2 算例及验证

为对所提的理论方法进行有效验证，现选取文献[8]中的4 组试验梁SFCB-1～SFCB-4，该试验梁均为加载一定周期的疲劳荷载后进行静力破坏加载测试其剩余承载力.其中，钢梁采用Q345 焊接而成，实测屈服强度为352 MPa，钢梁弹性模量为2.06×105MPa，栓钉直径为13 mm，所用钢材极限强度525 MPa，混凝土采用C50，其轴心抗压强度为38.3 MPa，弹性模量为3.59×104MPa.疲劳荷载为0.35 Pu～0.6 Pu，其中，Pu为静力极限承载力.组合梁的尺寸如图3所示.

试验结果表明，所选取的4 根试验梁除SFCB-1最终破坏模式为跨中混凝土压碎破坏外，剩余试验梁均为栓钉剪切破坏.其主要原因为随着疲劳加载次数的增加，剪力连接件承载力不断退化，试验梁由原先的完全抗剪转换为部分抗剪结构，塑性中和轴也由钢梁上翼缘板内下移至腹板内，从而影响最终破坏形态.根据试验结果和计算理论，其主要采用式（14）、（15）进行求解.

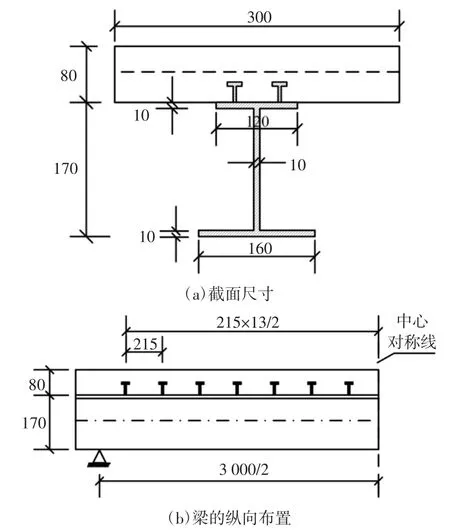
图3 试验梁尺寸（单位：mm）Fig.3 Test beam size（unit：mm）

同理，文献[6]中试验梁FSCB-2 在一定疲劳加载后未发生完全疲劳失效，从而继续对其进行剩余承载力试验，现选取其疲劳数据以对本文理论进行进一步补充验证.

表1 给出了该试验梁的疲劳加载后的剩余承载力试验值与理论值的比对.

表1 组合梁剩余承载力的理论值与试验值比对Tab.1 Comparison between the theoretical values of the residual bearing capacity of the composite beam and the test values

从表1 中可以看出，本文综合考虑栓钉、钢梁、混凝土板三者的退化模型所预测的组合梁承载力与试验测试值吻合较好，其最大误差控制在8%以内，说明所提方法能够对组合梁剩余承载力进行有效预测，因而可对组合梁实际情况下的疲劳性能进行初步判断，为工程设计人员提供有效参考.

3 参数分析

为研究组合梁在常幅疲劳加载情况下各构件退化规律，基于上述方法，现选取文献[8]中的SFCB 梁为基本研究对象，采用无量纲化处理，分别计算在加载过程中各个构件的强度折减，如图4 所示.

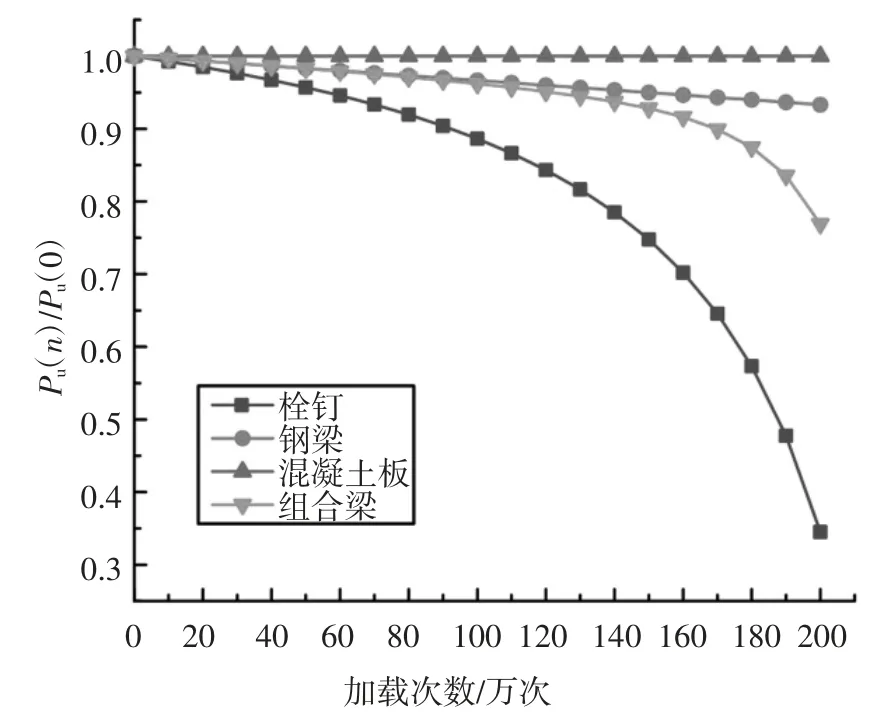
图4 组合梁各构件强度退化Fig.4 Strength degradation of each component of composite beam

从图4 可以看出，在疲劳荷载下，钢梁、混凝土板、栓钉连接件强度以不同速率发生折减，其中栓钉连接件折减速率最快，钢梁次之，混凝土板最慢，分析其原因主要为混凝土板在单轴受压疲劳荷载下疲劳寿命一般在107次以上，在经历200 万次疲劳加载后其仍处于寿命前期，疲劳损伤积累较小，相应强度折减较小，可忽略不计；加载前期，钢梁与组合梁下降速率较为一致，即其承载力退化由钢梁主导；在加载后期，组合梁下降速率明显加快，分析其原因主要为后期栓钉强度下降过快，从而成为影响整梁剩余承载力的控制因素.

为进一步对组合梁疲劳剩余承载力的关键影响因素进行研究，现分别就荷载幅值、栓钉初始缺陷、栓钉布置间距（即剪力连接度）进行讨论研究.

图5 中给出了组合梁在疲劳荷载下承载力退化的规律，其主要表现为在加载初期，随着疲劳加载次数增加，其承载力下降缓慢，基本成线性分布；随着加载次数的进一步加大，其承载力退化率也逐渐增加，并于后期基本呈指数型变化趋势，即在较短的加载次数范围内其承载力便发生大量折减.

图5 组合梁剩余承载力随疲劳荷载变化Fig.5 Variation of residual bearing capacity of composite beams under fatigue loading

其中图5（a）给出了不同加载幅值下组合梁承载力退化的曲线.从图中可以看出，加载幅值是控制承载力退化的重要影响因素.当加载幅值为0.2Pu时，组合梁承载力下降缓慢；当加载幅值为0.25Pu时，其承载力衰减速率已明显增加，经历200 万次时，承载力便下降了23.1%；当加载幅值为0.3Pu时，组合梁承载力下降速率进一步增加，其在经历200 万次疲劳荷载后便下降了39.6%，已难以满足正常承载要求，特别是在150 万次～200 万次，下降比率高达29.5%，即在加载后期承载力退化比率占了总比率的74.5%.

图5（b）给出了不同栓钉初始缺陷大小的组合梁承载力退化曲线.从图中可以看出，组合梁疲劳承载力退化率随着初始缺陷的增加而不断增加.当初始裂缝a0=1.5 mm 时，组合梁的剩余承载力退化速率较缓，其相对变化率在7%以内；当初始裂缝a0=2.0 mm 时，组合梁的剩余承载力退化速率加快，特别是在当初始裂缝a0=2.5 mm 时，其退化速率已非常迅速，在经历了160 万次疲劳加载后，其承载力便下降了近39%.

图5（c）给出了不同栓钉间距（亦即剪力连接度）的组合梁承载力退化曲线.从图中可看出，随着栓钉数量减少，间距增加（即剪力连接度降低），其承载力下降速率不断增加.当p=230 mm（剪力连接度为0.86）时，其经历160 万次疲劳荷载时，其承载力便降低了36.9%；而当p 进一步增加至250 mm（剪力连接度为0.71），其折减速率加快，在仅仅经历115 万次时，其承载力便降低了39.9%，已不适于正常承载.

基于以上分析可知，不同的疲劳应力幅、栓钉初始缺陷、栓钉间距（剪力连接度）的组合梁疲劳特性相差较大，因而在实际工程中，一方面需要对组合梁栓钉剪力连接度进行必要的设计，另一方面考虑到栓钉连接件是控制组合梁疲劳性能的关键因素，需要对其焊接质量进行精准控制.此外，应对车辆疲劳荷载进行控制以避免因应力幅过大而过早产生疲劳破坏.

4 结论

通过研究，可以得到如下结论：

1）通过引入考虑初始缺陷的基于断裂力学的栓钉承载力退化模型、钢梁及混凝土板的经典承载力退化模型，基于完全抗剪、部分抗剪承载力计算理论，本文建立了更为完善的用于计算钢-混组合梁疲劳荷载下剩余承载力的估算方法.该理论计算值与相关的试验梁测试值吻合很好，可以对实际工程中组合梁的剩余承载力进行有效预测.

2）组合梁各构件在疲劳荷载下发生不同程度强度折减，栓钉最快，钢梁次之，混凝土板最慢，且前期组合梁疲劳特性由钢梁主导，后期由栓钉连接件控制.

3）组合梁疲劳荷载下剩余承载力下降速率随着加载次数的增加呈现出不断增加趋势.在加载初期，下降速率较为缓慢，基本呈线性分布；加载后期，下载速率大幅增加，承载力下降趋势呈指数型分布.

4）剪力连接度、荷载幅值、栓钉初始缺陷这三者是影响组合梁剩余承载力退化程度的重要因素.随着疲劳荷载幅值的增大、栓钉初始缺陷的增大、栓钉间距增大（剪力连接度减小），其疲劳剩余承载力及达到同等剩余承载力所需的疲劳加载次数减少，因此需在实际工程中进行控制.