时延有界的PD-NOMA物联网高可靠接入算法

徐朝农，吴建雄，徐勇军

（1.中国石油大学（北京）信息科学与工程学院，北京 102249；2.中国科学院计算技术研究所，北京 100080）

1 引言

相对于一般的移动通信，应急通信对传输时延和可靠性同时有着更严格的要求，因为过时的、不可靠传输的数据对于应急通信应用意义有限[1]。因此，超可靠性低时延通信（URLLC,ultra reliable and low latency communication）被认为是下一代应急通信物联网的关键技术之一[1-3]。在物联网时代，网络中传感器的规模和数量有着几何级数的增长，这对通信时延和可靠性提出了更高的挑战[3-5]。

图1表示了功率域非正交多址接入（PD-NOMA,power domain non-orthogonal multiple access）技术的复用原理[6]。与传统的正交多址技术相比，基于串行干扰消除（SIC,successive interference cancellation）技术[7]，将用户复用的方式从传统的时域、频域和码域拓展到了功率域。在发射端，用户各自独立地进行数据发送；在接收端，用户采用SIC技术进行多用户解码[8]。SIC检测器通过串行方式解码，每一级只对一个用户进行解码，解码顺序则由各个用户在接收端的功率值所决定，功率越大的用户解码顺序越靠前。在接收机捕获了一个信号之后，对其进行重构，重构后在原有信号中将其消除。重复上述的SIC解码流程，直到所有用户全部完成解码。

图1 功率域NOMA示意

显然，非正交接入提高了并行接入的用户数，因此传输时延性能有所提升。然而，由于并行传输引起的高干扰，其传输可靠性受到很大影响[9]。因此，面对应急通信中的低时延高可靠上行传输需求，有必要找到一种方案，在保证实时性能的前提下，使上行传输的可靠性也能满足要求。

本文针对PD-NOMA技术，在传输时延有界的前提下，研究如何通过用户组配和功率分配来最大化上行传输的平均可靠性。基于此，本文设计了一种复杂度为O(nlogn)的启发式算法，并证明了该算法在2-SIC下是最优的。本文的贡献总结如下。

1)针对PD-NOMA的可靠性问题，构建了基于BPSK（binary phase shift keying）调制和k-SIC接收机条件下的闭式传输可靠性模型。这个模型不仅为本文、也为后续相关研究提供了坚实的数学模型，还为定量研究PD-NOMA下的传输可靠性奠定了理论基础。

2)在保证传输时延的前提下，以多用户的平均传输可靠性为优化目标，基于联合用户组配[10]和功率分配的方法，对问题进行了形式化建模，并在上述可靠性模型的基础上，提出了一种低复杂度的启发式算法。

3)从理论上证明了该启发式算法在2-SIC情况下是最优的。

2 相关工作

贝尔实验室对VBLAST（vertical Bell-labs layered space time）系统的可靠性进行了理论分析[11]，其研究的场景是MIMO（multi input multi output）应用，并非是多用户场景，但是其对SIC解码过程中可靠性的定量分析为目前PD-NOMA的可靠性分析提供了有益借鉴。文献[12]对文献[11]进行了改进，提出在BPSK调制下以递归式表示的误码率。文献[12]采用符号错误概率来定义可靠性，进而给出了系统中所有用户不能同时正确解码的概率，但没有给出系统误码率的期望。需要说明的是，文献[11-12]的研究对象是MIMO，和本文的多用户场景是完全不同的，因此误码率的模型不同。

文献[13]提出了单天线2-SIC下的误码率模型，但它在接收端使用了传统的星座图解码方式而非SIC解码。文献[14]在k-SIC条件下，寻找到使平均功率耗费最小的联合功率分配与最优组配策略。文献[15]在忽略SIC解码级的前提下，定义了PD-NOMA下的错误概率，以获得一个闭式的错误概率表达式。文献[16]分析了基于可见光的PD-NOMA下行通信下的可靠性问题。可见光涉及传输光的角度参数，与射频信号物理特性差距较大。文献[17]也分析了PD-NOMA下行传输的可靠性问题，这和本文研究的上行场景的区别很大，因为上行传输下SIC接收机特有的解码错误传递效应会更显著。

文献[18]分析了正交相移键控（QPSK,quadrature phase shift keying）调制下行传输的2-SIC误码率问题，给出了在瑞利衰落信道中下行传输中的误码率解析表达式，并且还给出了上行传输的误码率递推式。文献[19]基于瑞利分布对信道系数进行建模，进而得到了2-SIC下的错误概率解析表达式。文献[20]基于Nakagami-m衰落信道提出了PD-NOMA下行链路误码率的解析表达式。

相对上述在2-SIC下的工作，本文创新性地提出了单天线k-SIC下传输可靠性的闭式模型，因此本文工作为PD-NOMA可靠性的后续研究提供了有益借鉴。进而，基于该闭式模型，研究了多用户下的高可靠上行传输问题，并提出了相应的解决算法。理论分析和实验结果都充分说明了模型的客观性和算法的有效性。

3 可靠性模型与问题建模

本文考虑一个单跳单信道无线网络，网络中有n个单天线发送者和一个单天线接收基站。接收基站装有一个k-SIC接收器。一个k-SIC接收器最多可以同时解码k个用户信号。在这个网络中，收发者都采用BPSK调制解调，时间被划分为帧，每个帧被划分为时槽，信道增益在一个时间帧里保持恒定。假设所有用户的最大传输功率均相同，为Pmax。所有用户的发送功率连续可调，采用完美的SIC技术[21-22]。

为了便于理解，本文首先根据信号解码的错误概率分布，在3.1节针对2-SIC情况推导出一个信号传输可靠性模型，并在3.2节将其推广到k-SIC下。在这个模型的基础上，3.3节对所研究的问题进行了建模。表1列出了本文主要变量的定义。

表1 本文主要变量的定义

3.1 2-SIC下的可靠性模型

为了便于理解k-SIC下的可靠性模型，本文先考虑2-SIC接收机。当Ua和Ub同时向接收端传输信号时，接收端的信号Y可以表示为

其中，Pa和Pb分别是Ua和Ub的发送功率，Ga和Gb是它们各自的信道增益；n0是加性高斯白噪声，服从N(0,б)分布，б2是噪声功率；Xa和Xb分别是Ua和Ub发送的信号，当Ua发送1时，Xa=1，当Ua发送0时，Xa=-1，Ub同理。将式(1)归一化，得

定义1当Ua以功率Pa发射时，称为Ua的归一化接收幅度，记为Aa。

因此，式(2)可改写为

假设Ua和Ub同时传输数据，它们的归一化接收幅度分别为Aa和Ab。不失一般性，假设Aa＞Ab。根据SIC解码原则，Ua会被首先解码。如图2的归一化接收信号所示，当Ua和Ub同时发送数据0时，Xa被判定为+1的归一化接收信号幅度区间为(0,∞)。如果Ua被正确解码，那么Xb被判定为+1的归一化接收信号幅度区间则为(-Aa,0)。此时Ua的错误判决概率为

其中，(0,0)表示Ua和Ub均发送数据0，Q(.)为Q函数，且

只有当Ua被正确解码时，Ub才有可能被正确解码。因此，在Ua正确解码的前提下，Ub正确解码的概率为

类似地，当Ua和Ub都发送数据1时，可得

以上揭示了Ua和Ub传输相同数据时的位错误率。同理，当Ua和Ub传输不同的数据时，也可以用相似的方法得出以下结论。

如图3所示，当Ua传输0、Ub传输1时，Ua的错误判决区间为(0,+∞)；如果Ua被正确解码，Ub的错误判决区间为(-∞,-Aa)。那么

类似地，可得P((Xa=-1)|(1,0))=P((Xa=1)|(0,1))。

图3 当Ua和Ub分别传输0、1时2-SIC的解码错误判决区间

综上各种情况，并且考虑到经过信源编码后，用户发送0、1的概率相同，因此误码位数的期望为

而平均误码率为误码数量和传输位数的比值，单时槽2-SIC条件下传输位数为2，因此误码率为

3.2k-SIC下的可靠性模型

本节将上述2-SIC的分析方法推广到k-SIC。为了总结出一般规律，先将误码率模型推广到3-SIC，以获得推广的启示。为标识清晰，本节将角标由字母变换为数字。

在SIC解码的过程中，错误具有传递性。即当任何一个用户解码错误，解码过程立即终止，尚未解码的用户不再进行解码，按照误码进行处理。3个用户U1、U2和U3同时传输数据，它们的归一化接收幅度分别为A1、A2和A3。不失一般性，假设A3＞A2＞A1。

当3个用户都传输0时，仍然根据高斯白噪声的概率式，以及BPSK的解码判决机制来寻找位错误率，具体如图4所示。

1)当接收的归一化信号幅度在(0,∞)时，X3被判定为+1，U3解码错误。根据错误的传递性，此时用户U3、U2和U1均解码错误，错误位数为3。

2)当接收的归一化信号幅度在(-∞,0)时，U3解码正确，此时继续判决用户U2如下。

2.1)当接收的归一化信号幅度在(-A3，0)时，X2被判定为+1，U2解码错误。根据错误传递性，U2、U1均错，此时错误位数为2。

2.2)当接收区间为(-A3-A2，-A3)时，U3、U2解码成功，用户U1解码错误。此时错误位数为1。

综合上述情况，当用户U3、U2和U1均传输0时，误码位数的期望为

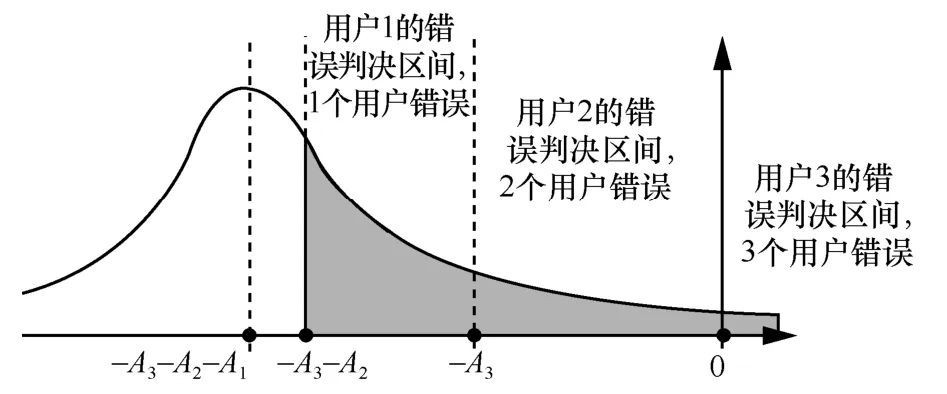
图4 当3个用户都传输0时3-SIC的解码错误判决区间

同理，可得3个用户传输其他数据值时的误码个数。

综合其他情况，可得3-SIC的误码率表达式如式(11)所示。4-SIC的误码率表达式也可依此方法得出，如式(12)所示。

由式(11)以及式(9)可知，3-SIC解码过程中包含了完整的2-SIC解码过程，也即解码完功率最大的用户之后，即为2-SIC解码过程。同理，4-SIC解码过程中包含了3-SIC解码过程。这为本文获得k-SIC下的位错误率的闭式表达式提供了有益的启示。

定理1k-SIC接收机的误码率为

其中，j为SIC解码层数，取值范围为为下取整操作。考虑解码层数为j时，(A1,A2,…,Aj)的取值组合共有2j-1种，用i代表这2j-1个信号幅度的取值组合的序号，有

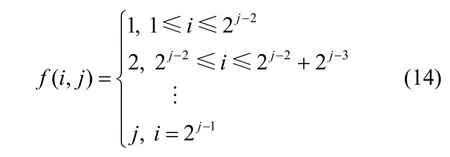
证明利用数学归纳法进行证明。当只有一个用户传输时，显然成立。假设l（l＜k）个用户传输时，误码率表达式成立。下面对第l+1个用户传输时的情况进行分析。

为了获得一个相对直观的理解，本文先分析当用户U1～Ul全传0，新加用户Ul+1也传0时的情况。一方面，如图5所示，当接收到的复合信号值时，由于X1=…=出现该情况的概率为Q(Al+1+…+A1)。此时，Ul+1解码错误，并导致U1～Ul全部误判，即错了l+1位。而此时，由于因此Ul将必定被译码为1，并导致U1～Ul-1全部误判，也即译码错了l位。从而，错误新增了1位。综上所述，得到

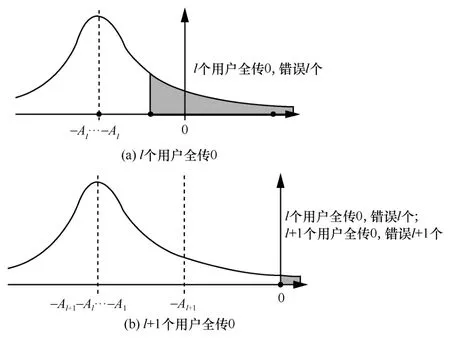
图5 当l个用户和l+1个用户均传输0时的解码错误判决区间

当U1～Ul全传1，新加用户Ul+1传0时，如图6所示，当接收到的复合信号值-Al+1+Al+…+＞0时，由于因此出现该情况的概率为此时，Ul+1解码错误，并导致U1～Ul全部误判，即错了l+1位。而此时，由于，因此U1～Ul将全部被正确判决，从而，错误新增位数为l+1。综上所述，得到

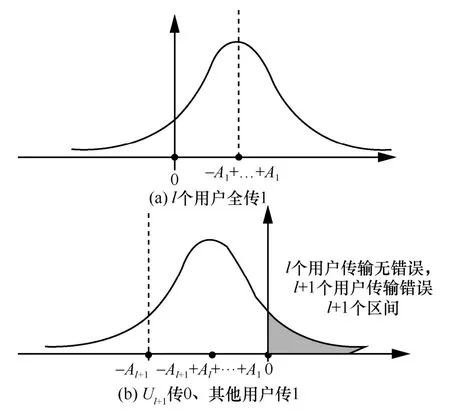
图6 当l个用户全传1和Ul+1传0、其他用户传1时的解码错误判决区间

一般情况下，当U1～Ul传输某个确定的值（用C代表该值）时，接收的复合信号值的概率分布曲线的中心点坐标记为S。当Ul+1发射0时，概率分布曲线中心点将平移至S-Al+1，此时，对Ul+1判决错误的概率为Q(Al+1-S)；当Ul+1发射1时，概率分布曲线中心点将平移至S+Al+1。此时，对Ul+1判决错误的概率为Q(Al+1+S)。

Ul+1和Ul传输数据位相同的情况共有2l-1种，此时新增错误位数为1；Ul+1和Ul传输数据位不同，但是和Ul-1传输数据位相同时共有2l-2种，此时新增错误位数为2。依次类推，Ul+1与Ul,Ul-1,…,Ul-s传输数据位均不同，且与Ul-s-1传输数据位相同的情况为2l-s-2种，此时新增错误位数为s+1。

把式(13)的BER(A1,A2,…,Al)及S的表达式代入上式，得到的表达式恰为与式(13)相同的BER(A1,A2,…,Al+1)。从而，当有l+1个用户时，式(13)所代表的误码率公式仍成立。证毕。

3.3 问题描述

定义2可靠的k-SIC上行链路调度问题。在一个单跳网络中包含一个配备了基于BPSK的完美k-SIC接收器的基站。U1,U2,…,Un共n个用户为发送端，对应的信道增益分别为G1,G2,…,Gn。不失一般性地，假设G1≥G2≥…≥Gn。所有用户的最大发送功率相同，噪声功率也相同（均为б2）。记用户的发送功率分别为p1,p2,…,pn。对这些用户进行用户调度以及功率分配，当满足1)每个用户在同一帧里面只调度一次；2)帧长不超过指定的长度L时，用户的平均误码率最小。

问题可以描述为

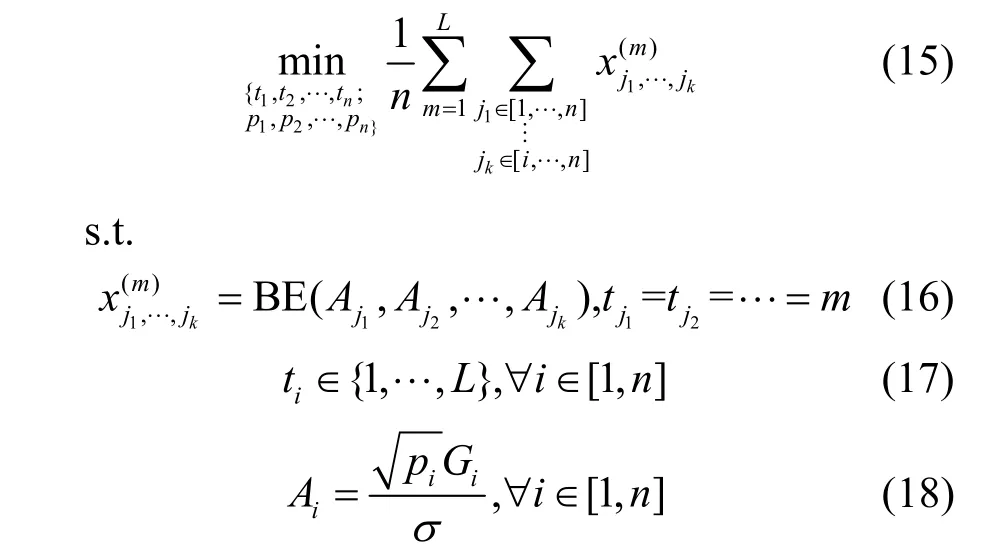
其中，ti是Ui被调度时的槽序号；j1～jk是同一个时槽中的k个用户；系统的可靠性受{t1,t2,…,tn}和{p1,p2,…,pn}共同影响，它们分别是用户组配策略和功率分配策略；L是帧长限制，用于衡量实时性能（用户的最大接入时延不会超过一个帧的时长，其值可参考文献[13]，这里不进行赘述）；k是单时槽内最多可同时解码的用户数，即k-SIC中的参数k。

4 问题的快速求解

可靠的k-SIC上行链路调度问题似乎是一个组合优化问题，因此，如果通过基于优化的算法解决它，将会导致高的时间复杂度。本文提出了一种启发式的策略，并依据此启发策略提出低复杂度的算法，其思路为将原始问题顺序分解成用户组配和功率分配子问题，然后分别求解。4.1节提出一个启发式用户组配策略，4.2节则介绍了单时槽下的启发式功率分配策略，将4.1节与4.2节的算法顺序联合在一起，就得到了最终的快速启发式算法。目前本文还无法证明该算法在k-SIC下是最优的，但在第5节证明了当k=2时该算法是最优的，这已经能够满足绝大多数的应用场合[9]。

4.1 启发式用户组配策略

若时延上界为L，则从传输的平均可靠性角度考虑，用户要尽量均匀分布在这L个时槽中。之所以采取这个策略是因为在一个时槽内，用户功率将会随用户数呈指数增长趋势，从而会给其他用户造成大的干扰，导致可靠性下降。对于U1,U2,…,Un，如果最大时延限制为L个时槽（显然，只有n≤kL满足时才可能满足要求），那么一个启发式的组配策略如算法1所示。

算法1k-SIC启发式用户组配算法

输入用户U1,U2,…,Un，用户到基站的信道增益CG[n]，规定的时延界L

输出用户组配策略GM[L]

步骤1将用户按照它们的信道增益升序排列，不失一般性，假设CG[i]≤CG[i+1]，i=1,2,…,n-1；

步骤2将每个用户排序后的编号模L取余，余数相同的用户分到一组，得到GM[L]；

这里，用户Ui的最大归一化接收幅度为。对于U1,U2,…,Un，如果它们已经按信道增益升序排列，则最后生成的用户组配策略为{{U1,UL+1,…};{U2,UL+2,…};…;{UL,U2L,…}}（不考虑时槽之间的先后关系）。

4.2k-SIC单时槽启发式功率分配策略

基于4.1节的误码率解析表达式，本节提出单时槽内的功率分配的一个启发式策略[12,23]。

引理 1BER(A1,A2,…,Al)是一个关于Al的减函数。

证明根据式(13)可知，由于，因此BER(A1,A2,…,Al)关于Al单调递减。

引理1说明，为了最小化平均误码率，第一个被解码的用户的接收功率应该取其最大值。

从而可得，一个启发式的功率分配算法如算法2所示。对于l（l≤k）个并行用户U1,U2,...,Ul，假设它们的最大归一化接收幅度满足也即它们的解码顺序为Ul,…,U1，用户Ul的发射功率应设置成最大。对于Ul-1用户的功率设置，则在把用户U1,U2,…,Ul-2的发射功率都设置为0的前提下，通过求导使最小的功率值Al-1即可，其余用户依次类推。

下面，对k-SIC功率分配算法进行解释。步骤1为让最先解码的幅度最大，求得归一化接收信号幅度的最佳值Ak，这一步的合理性已经在引理1中得到证明。步骤2将步骤1中得到的Ak代入式(13)，并求得第k-1层的最优接收幅度，依次类推，直至所有用户功率都确定。最后将归一化接收幅度转化为发射功率。

4.3k-SIC下的启发式算法

将算法1和算法2组合起来，得到算法3，它是求解可靠的k-SIC上行链路调度问题的一个启发式算法。

算法3k-SIC下的启发式算法

步骤1按算法1得到用户组配策略；

步骤2在每个时槽中按算法2得到用户发射功率；

显然，算法3的复杂度为O(nlogn)，实质是快速排序算法的复杂度。

5 2-SIC下算法3的最优性

5.1 2-SIC下单时槽功率分配的最优性

首先说明在单时槽2-SIC的情况下，算法2是可靠性最优的功率分配算法。

引理1已经说明了为达到本时槽内的最高可靠性，第一个被解码的用户（标记为Ua）的功率应该尽可能大。接下来，引理2表明，此时Ub的最优功率解是唯一的。

引理2对于任意指定的Aa，当Aa＞5时，Ab有使BER(Aa,Ab)最小的唯一值。

综上所述，当第一个用户以满功率发送，而第二个用户控制功率，使其归一化接收幅度为时，此时在该时槽内的可靠性最优。为方便起见，记其为

5.2 2-SIC下用户组配的最优性

如果Ua和Ub共享一个时槽，它们的平均位错误率被表示为BER(Aa;Ab)，其中

引理33个用户Ua、Ub和Uc，如果它们的归一化接收幅度满足Aa＞Ab＞Ac，有以下不等式成立。

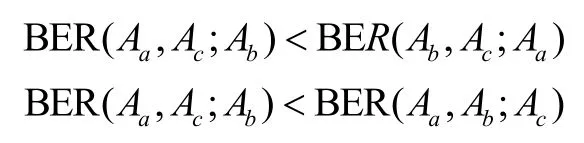
证明先写出3种不同组配关系下的误码率表达式BER

证毕。

有了上述的铺垫，下面，本文去寻找最优解满足的必要条件。

定理2如果L≤n≤2L，对于可靠的2-SIC上行链路调度问题的最优解，一定没有空闲的时槽。

证明 如果最优解有空余时槽，根据抽屉原理，那么一定存在某个时槽，其中有2个用户。假设这2个用户为Ui和Uj，它们相应的信道增益Gi＞Gj。因此，它们的最大归一化接收功率满足

根据引理2和引理3，针对这2个用户，它们的平均最小误码率为

然而，如果Ui和Uj分别在2个不同的时槽传输，则它们最优的误码率为

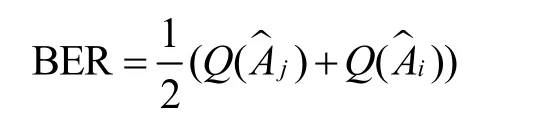
因为Q(x)是x的减函数，所以这与假设的最优解矛盾。证毕。

因此，如果2个用户分别在不同的时槽内传输，可以得到更低的误码率。综上，最优解的必要条件之一为L个时槽都被利用起来，没有空时槽出现。接下来的2个定理揭示了任意2个时槽之间的最佳用户配对策略，这2个定理是2-SIC最佳用户组配策略的关键所在。

定理3对于3个用户U1、U2和U3，它们最大归一化接收幅度分别为且满足如果它们在2个时槽内传输，那么它们的最优组配关系为{{U3,U1};{U2}}，即U1和U3共享一个时槽，U2单独占用一个时槽。

证明显然有3种可能的组配方式，α1={{U3,U1};{U2}}、β1={{U2,U1};{U3}}和γ1={{U3,U2};{U1}}。下面直接比较3种组配关系的误码率。

由引理1、引理2和定理2可知，α1的最优功率分配方式为β1的最优功率分配方式为，γ1的最优功率分配方式为

1)比较α1和β1的误码率

综上，α1是3个用户在2个时槽传输的最优用户组配策略。证毕。

定理4对于4个用户U1、U2、U3和U4，假设它们的最大归一化接收幅度分别为和并且满足。如果它们在2个时槽内传输，那么它们最优的组配关系为{{U1,U3};{U2,U4}}，即U1和U3在同一个时槽内传输，同时U2和U4共用一个时槽。

证明显然，一共有3种组配关系，分别是α2={{U1,U3};{U2,U4}}、β2={{U2,U3};{U1,U4}}和γ2={{U1,U2};{U3,U4}}，下面对这3种组配关系分别进行比较。

综上，α2是2个时槽4个用户下的最优用户组配策略。证毕。

显然，可靠的2-SIC上行链路调度问题的最优解必须满足定理2、定理3和定理4。经分析发现，满足这3个定理的解竟然是唯一的。也就是说在2-SIC的情况下，算法3输出的解是唯一最优解。举例如下：对于U1,U2,…,Un，假设它们的信道增益呈降序排列，如果时延最高为个时槽，那么最优的组配策略必定如图7所示。其理论证明如定理5所示。

图7 2-SIC条件下的最优解

定理5在2-SIC的情况下，算法3输出的解是唯一最优解。

证明反证法。如果还有另一种组配及功率分配方式，它与算法3的输出不同，则它一定会违背最优性的必要条件。具体来说，如果它的所有时槽都是有2个用户，则它一定违反定理4。如果存在一个包含2个用户的时槽和另一个只有1个用户的时槽，则它一定违反定理3。总之，找不到比算法3输出的更优的解。证毕。

6 实验仿真

本文的模拟参数设置如下。所有用户随机部署在环形区域内，其内半径和外半径分别为500 m和1 200 m，并且在中心处有一个k-SIC接收基站。噪声功率为-126 dBm，功率谱密度为-173 dBm/Hz，带宽为50 kHz。所有用户的最大发射功率为16 dBm。信道增益模型为CG=-20log(f)-26log(d)+19.2，其中，d为用户到基站的距离，f=5 GHz。

6.1k-SIC下的性能比较

如图8所示，本文设置了25个用户在5-SIC下、20个用户在4-SIC下、15个用户在3-SIC下的情况，时延界限L在5～15变化。用户按照算法3进行传输。在每种情况下，随着时延参数L的逐渐增大，每个时槽内的用户数逐渐减少，此时，误码率会显著下降。注意，图8纵坐标为对数坐标，误码率随着时延的下降呈指数下降。系统可以通过组配算法迅速达到可靠性最优。

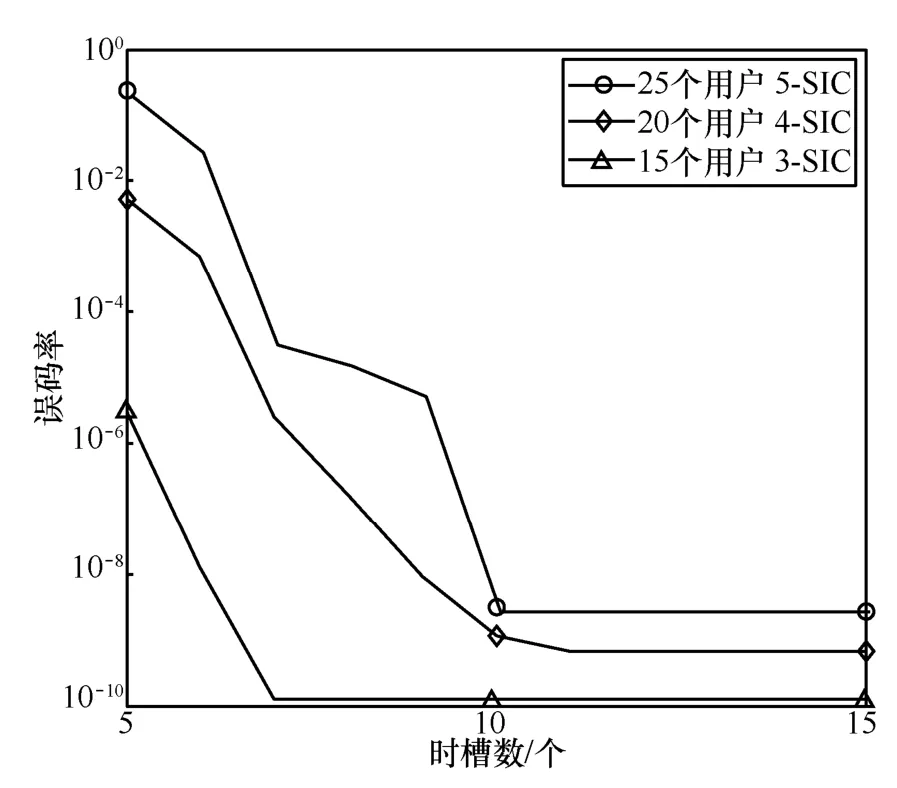
图8 不同时延、用户数和k值下的k-SIC平均误码率

从图8中可以看出，这几条曲线均有一段可靠性较平坦的区域，平均误码率无法随着时延界限的放宽而继续降低。主要原因是：对于离基站距离较远的用户，其信道增益很低，因此很难降低该用户的BER，从而其所在的整个时槽的BER也难以降低。

PD-NOMA应用的主要缺陷在于其功率消耗比较大。图9为在与图8相同条件下的每个节点的平均发射功率，即在L个时槽下，所有节点发射功率的平均值。从图9中可以看出，在给定用户数下，随着最大时延的增加，用户平均功率在增加，这是因为为了最优化可靠性，越多的用户采用高功率发射。而在相同的最大时延情况下，当L=5时，图9的3种仿真实例中，每个时槽分别为3、4、5个用户，因此与其他2个实例相比，15个用户实例的高功率用户相对比例会更大，从而节点平均功耗最大。而随着L的进一步增大，这种高功率用户的比例差距会逐步缩小，因此节点平均功耗也会逐步趋向一致。可以看出，节点平均功耗主要受高功率节点比例值的影响，当最大时延越大（小于节点数目的前提）时，平均功耗会越大，当然，其传输可靠性也会增强。

6.2 2-SIC下算法3的最优性

如图10所示，本文分别设置了30、40、50个用户的场景，时延界限L在15～50变化。从图10中可以发现，对于给定的用户数，平均BER均随时延范围的增加呈指数下降。在相同的时延限制要求下，平均BER总是随着用户数量的增加而增加，这个现象是合乎理论的。50个用户对应的曲线末端比较平滑，这是因为由于用户数量和时延界限都比较大，因此用户组配策略有了更大优化空间，因此不会带来可靠性性能的迅速变化。

图9 不同时延、用户数和k值下的k-SIC平均功率

图10 2-SIC下算法3和随机算法的平均误码率

虽然已经在理论上证明了算法3在2-SIC下具有最优可靠性，本文在实验中又加入了其与其他一般性算法的对比，使用随机算法来表征其他一般性算法。算法实质是随机选择用户组配策略，并在所选定的组配策略下按照算法2确定发射功率，计算出平均误码率后再以此指标作为策略留存的依据。经过一段时间的迭代比较，最终收敛到一个局部最优策略。显然，在可靠性指标上，算法3明显优于随机算法。

7 结束语

本文分析了基于PD-NOMA的物联网可靠接入问题。通过建立信号级误码率模型，提出了启发式算法，并证明了该算法在2-SIC情况下的唯一最优性。理论证明和性能评估均验证了所提算法的有效性。传输可靠性是无线网络的重要指标。由于PD-NOMA是下一代无线网络的候选媒体访问技术标准，因此，为其找到用于高可靠通信的快速算法是必不可少的。本文的研究结果为下一代高可靠低时延物联网奠定了理论和技术基础。