基于Matern簇过程的NOMA-HetNet覆盖概率分析

景小荣，陈怡西，陈前斌

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.重庆邮电大学移动通信技术重庆市重点实验室，重庆 400065）

1 引言

作为第五代无线移动通信系统（5G,5th generation）新兴无线网络架构技术[1]的重要组成部分，密集异构网络（HetNet,heterogeneous network）[2]通过密集部署多种类型的基站（BS,base station），缩小了用户（UE,user）与无线接入点间的距离，大幅提升了网络的覆盖能力；同时，非正交多址接入（NOMA,non-orthogonal multiple access）采用非正交资源分配方式来容纳更多用户，使频谱效率得到显著提升[3]。将NOMA应用在HetNet中，形成NOMA-HetNet，可在增强通信覆盖的同时，使系统所服务的UE数量得到进一步提升，因此，NOMA-HetNet引起了学术界的极大关注[4]。

由于网络的随机性和不规则性[5]，随机几何近年来被广泛应用于HetNets的建模中，常用的方法包括泊松点过程（PPP,Poisson point process）和泊松簇过程[6]（PCP,Poisson cluster process）。在基于PPP的HetNet研究中，文献[7]将随机几何模型从无线自组织网络中推广到多层HetNet，推导了覆盖率、中断率和平均可达速率的表达式；但各层BS和UE被假设为完全相互独立的PPP，没有考虑节点间、用户间的相关性。

现实中，在一些热点区域，UE通常成簇分布，与BS间存在一定的耦合性。最新研究表明，由PPP引申出的PCP非常适合用来表征网络节点的空间相关性，它能够利用点的聚类效应，弥补3GPP提出的HetNet模型实例与基于PPP对HetNet进行分析的差距[8-9]，其中最受欢迎的包括Thomas簇过程（TCP,Thomas cluster process）和Matern簇过程（MCP,Matern cluster process）。基于此，学者们对HetNet的结构进行了细致的理论研究，其中文献[10]讨论了PPP和PCP混合分布时的网络模型，并利用PCP中的相关距离分布和干扰的拉普拉斯变换推导出了覆盖概率的积分表达式；而文献[11]则采用PCP建立了以用户为中心的双层HetNet网络模型，将宏基站（MBS,macro base station）建模为PPP，小基站（SBS,small base station）和UE均建模为TCP，进而在基于最小距离和最大平均接收功率2种关联准则下，讨论了系统参数与关联概率和覆盖率的关系。由于在基于PPP和PCP的HetNet模型中，推导覆盖率和中断率时均离不开用户与传输节点间距离的分布特性，因此，文献[12]和文献[13]基于TCP和MCP分别讨论了最近邻距离和接触距离的分布特性。

随着NOMA技术的兴起，基于随机几何理论，针对NOMA的研究成为热点。文献[14]采用PPP建立了下行NOMA系统分析框架，通过求解信道增益的分布特性，推导了用户覆盖率和平均可达速率的表达式；文献[15]研究了NOMA中串行干扰消除（SIC,successive interference cancellation）引起的错误传播率对系统性能的影响。然而，这两项研究均未考虑UE与BS间的关联性。以各BS为中心，采用NOMA技术为固定数量的用户提供服务，文献[16]在分析覆盖概率之余，提出了最大化小区和速率的功率分配算法，并证明了残留的小区间干扰较小时，NOMA较正交多址接入（OMA,orthogonal multiple access）能获得更高的小区和速率。上述工作研究了融合NOMA技术且具有随机几何特性的单层网络，但对于涵盖了多种类型基站的HetNet而言，这些工作存在一定的局限性。此外，采用SIC技术抑制簇内干扰时，文献[14]假设信道增益大的强用户总是能成功解码弱用户信号；在文献[16]中，强用户若不能解码弱用户信号，该强用户便不能成功解码。两者分别考虑了SIC解码时的最好和最坏情形，然而在实际情况中，强用户不能总是成功解码弱用户信号，解码弱用户信号失败时，也有可能成功解码自身信号。这些不足在现有工作中均未充分考虑。

针对NOMA-HetNet，学者们进行了有意义的探讨和研究。文献[17]阐述了NOMA对5G HetNet容量提升的意义，证明了在HetNet中实行NOMA或混合多址接入方式时，采用多种用户配对方案均能有效提高系统和速率，但没有考虑网络的不规则性，忽略了BS和UE在空间分布上的相关性和随机性。针对双用户NOMA-HetNet场景，考虑层内和跨层干扰并存时的干扰管理问题，文献[18]研究了最大化和速率目标下，联合频谱分配和功率控制的优化问题，证明了其提出的NOMA增强型HetNet在和速率和用户连接性方面均显著优于基于OMA的HetNet；文献[19]则在该场景下，重点研究了基于压缩感知理论的干扰管理方案，表明在NOMA-HetNet系统中，采用合适的干扰管理技术，系统和速率和中断概率方面的性能较OMA更优。但文献[18-19]是在已完成用户关联方案的前提下进行的研究，存在一定的局限性。针对多小区多用户NOMA-HetNet场景，文献[20]融合5G中的能源协作技术，研究了可再生能源和常规电网2种方式为BS供能情况下，最大化能效的资源分配算法，证明了NOMA可以实现比OMA更高的能效性能。尽管上述工作从不同角度证明了NOMA应用在HetNet中提升系统整体性能的优势，但鲜有研究考虑BS和UE在空间上的相关性，关注基于随机几何的NOMA-HetNet中用户的性能。

在上述分析的基础上，针对现有研究工作的不足，本文的创新工作总结如下。

1)根据网格的不规则性和UE与BS间的相关性，将MBS建模为PPP，SBS和UE共同建模为PCP，提出了一种基于MCP的NOMA-HetNet模型，为NOMA-HetNet部署提供了一定理论支撑。

2)为了分析系统中UE覆盖概率，提出了利用空间坐标系、概率论、随机几何理论和顺序统计量等数学工具来求解关联概率和服务距离分布特性的思路。所得结果有助于分析实际情况中节点间存在相关性的无线网络性能。

3)针对现实中的非完美SIC方案，根据弱用户信号是否解码成功，给出了一种更符合实际情况的信干噪比（SINR,signal to interference plus noise ratio）上限更新规则，并基于此，利用干扰的拉普拉斯变换推导了用户覆盖概率的理论表达式。

4)给出的基于MCP的双层NOMA-HetNet模型具有一般性，可扩展到其他PCP（如TCP）或基于其他关联准则的网络中。

2 系统模型

本节给出基于MCP的新型NOMA-HetNet模型，具体包括空间网络模型、关联策略及用户成簇方式。

2.1 空间网络模型

考虑如图1所示的双层超密集异构网络模型。其中，MBS建模为强度为λm的齐次泊松点过程（HPPP,homogeneous Poisson point process），Φm≡{m0,m1,m2,…}表示网络中所有MBS的位置矢量集合，对MBS所在宏小区基于Voronoi图进行划分；SBS和UE共同建模为MCP，即SBS为MCP的父过程点，假设这些父过程点为强度λs的独立HPPP，Φs≡{s0,s1,s2,…}表示网络中所有SBS的位置矢量集合；UE建模为MCP的子过程点，假设N个UE均匀地分布在以SBS为圆心，R为簇半径的圆内。令表示系统中的所有UE，其中表示SBSs覆盖范围内的UE位置矢量集合。于是，在单个宏小区内，近似分布着表示四舍五入取整操作。

根据MCP的定义，SBSs覆盖范围内的任意UEu的概率密度函数（PDF,probability density function）为

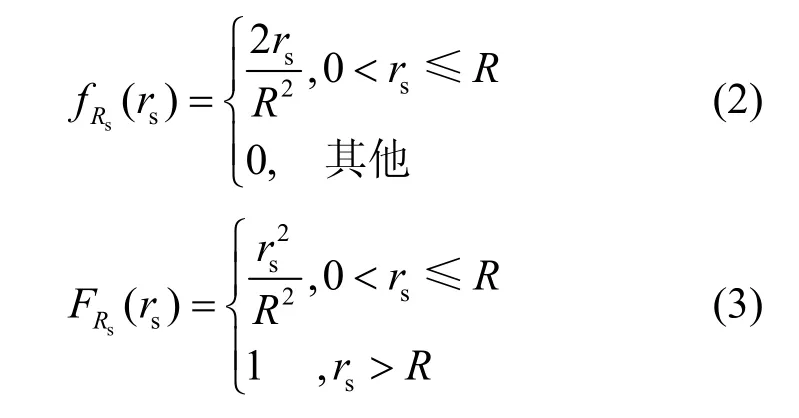
图1 双层超密集异构网络模型

根据HPPP的性质[21]，SBS与距其最近的MBS之间的距离rb的PDF和CDF分别如式(4)和式(5)所示。

2.2 关联策略及用户成簇方式

如图1所示，系统中每个UE有2个候选关联BS，分别为父过程点SBS、父过程点SBS所在宏小区内的MBS。基于平均接收功率最大化原则，UE选择其中之一关联。关联同一个BS的UE，形成一个簇，采用NOMA技术与关联BS进行通信。

不失一般性地，假设典型UEu0位于典型SBSs0的小小区内，典型SBSs0位于典型MBSm0的宏小区内，则与UEu0关联的BS可表示为

3 SINR分析

4 覆盖概率分析

覆盖概率定义为UE实现目标SINR的概率，即UE的实际SINR大于门限γ的概率，则在本文的NOMA-HetNet中，UE的平均覆盖率可表示为

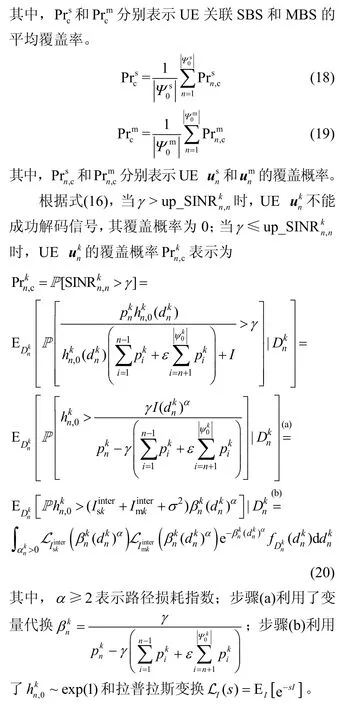
从式(20)可看出，除了需要比较SINR上限与γ的大小外，为求覆盖概率，还需要给出UE关于干扰的拉普拉斯变换、服务距离的PDF和功率分配方案。下面将在给出SINR上限更新规则的基础上，对所需的各部分进行详细的理论分析。

4.1 SINR上限更新规则

针对现实中非完美SIC方案，本节给出了一种更符合实际情况的SINR上限更新规则。

在文献[14]中，信道增益大的强用户总能成功解码弱用户信号，而根据式(16)可知，并非恒成立，即强用户未必总能成功解码弱用户信号；在文献[16]中，强用户若不能解码弱用户信号，该强用户便不能成功解码，而根据式(16)，当时，不一定有，即强用户解码弱用户信号失败时，也有可能成功解码自身信号。两者分别考虑了SIC解码时的最好和最坏情形。在实际情况中，强用户未必总能成功解码弱用户信号；同时，即使解码失败，也有可能成功解码自身信号。本文考虑强用户采用SIC解码弱用户信号时，若不能成功解码，则将该弱用户的信号视作簇内干扰信号继续解码。

4.2 干扰的拉普拉斯变换

4.3 服务距离分析

本节重点关注NOMA-HetNet下服务距离的分布特性。服务距离定义为UE与关联BS间的距离，而服务距离分布则对应地是UE关联某个特定BS下的条件分布，于是，UE与关联SBS间服务距离Ds＞ds和UE与关联MBS间服务距离Dm＞dm的概率可分别表示为

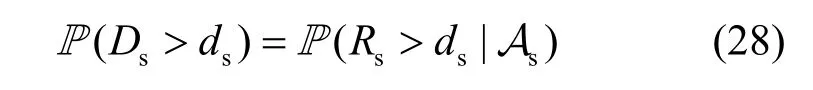
为了得到服务距离的分布特性，需要求出UE与SBS或MBS间的距离分布和UE关联SBS或MBS的概率，而UE与SBS间的距离分布已由式(2)和式(3)给出。下面分析UE与MBS的距离分布特性和UE关联SBS或MBS的概率。

4.3.1典型UE与典型MBS的距离分布

步骤1给定典型SBS与MBS间距离rb，推导典型UE与MBS间距离rm的条件分布特性。

如图2所示，以典型MBSm0为原点，MBSm0与SBSs0所在直线为横轴，建立直角坐标系，则m0=(0,0),s0=(rb,0)，同时令u0=(u1,u2)表示典型用户的坐标位置，则。根据MBS是否在SBS覆盖范围内，典型用户的坐标范围有所不同，因此，下面对rb≤R和rb＞R这2种情况进行分析，其中R表示典型SBS的覆盖半径。

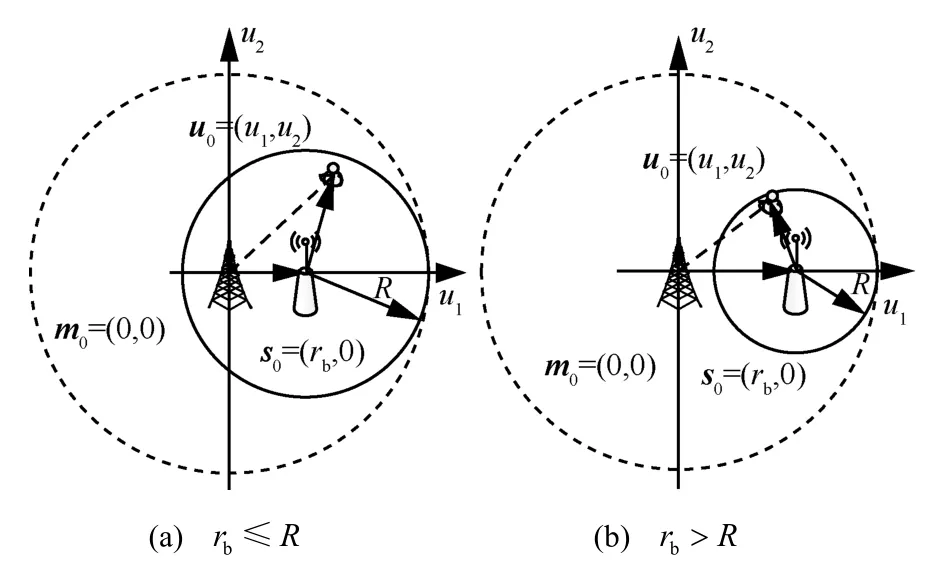
图2 UE、SBS和MBS的空间位置关系

根据图2所示的空间位置关系，当rb≤R时，有0≤rm≤rb+R；当rb＞R时，有rb-R≤rm≤rb+R。进一步地，考虑到rm在[0,R-rb]和(R-rb,R+rb]2个范围内变化时，图2(a)中典型UE的u0=(u1,u2)分布的区域将不同。因此，结合rm的3种取值情况（如图3所示），下面将展开具体分析，其中b(o,a)表示以o为圆心，a为半径的圆域。

1)rb≤R

当0≤rm＜R-rb时，典型UE的位置如图3(a)中D1区域所示，其中D1=b(s0,R)∩b(m0,rm)，结合式(1)，当典型SBS与MBS间距离rb给定时，典型UE与MBS间距离rm的CDF为

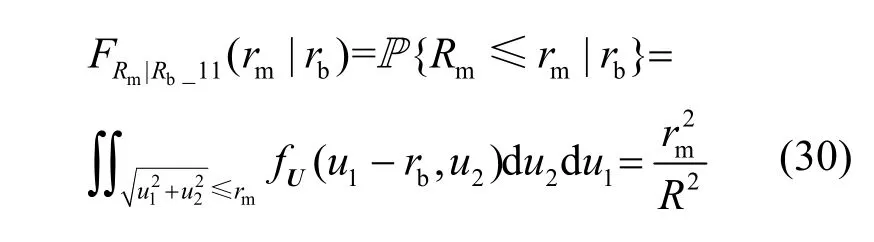
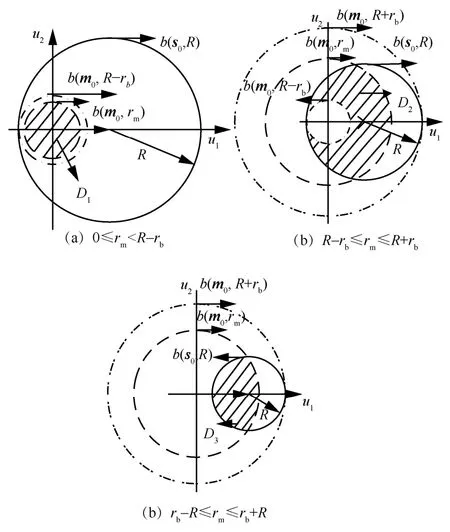
图3 UE的3种位置示意

进而有

综合参考学生认知水平、教学目标，进行问题情境的创设，以此来激发学生的能动性。与此同时，遵循循序渐进的原则，将问题设计成递进的问题，引导学生跟随问题进行思考、探究，并通过实践验证掌握技术要领，这能增强学生的探究能力、促进学生智力的发展。

步骤2推导典型UE与MBS间距离rm的分布特性。

根据rm的分段特性，需分3段来推导，具体如图4所示。

图4 分段求解rm示意

4.3.2关联概率

本节给出UE关联SBS/MBS的概率。记UE关联SBS为事件As，UE关联MBS为事件Am，则UE关联SBS的概率分布为

UE关联MBS的概率分布为

4.3.3UE与关联SBS/MBS的服务距离分布

由4.3.1节和4.3.2节分析可得出UE与关联SBS/MBS的服务距离分布，如式(43)～式(46)所示。

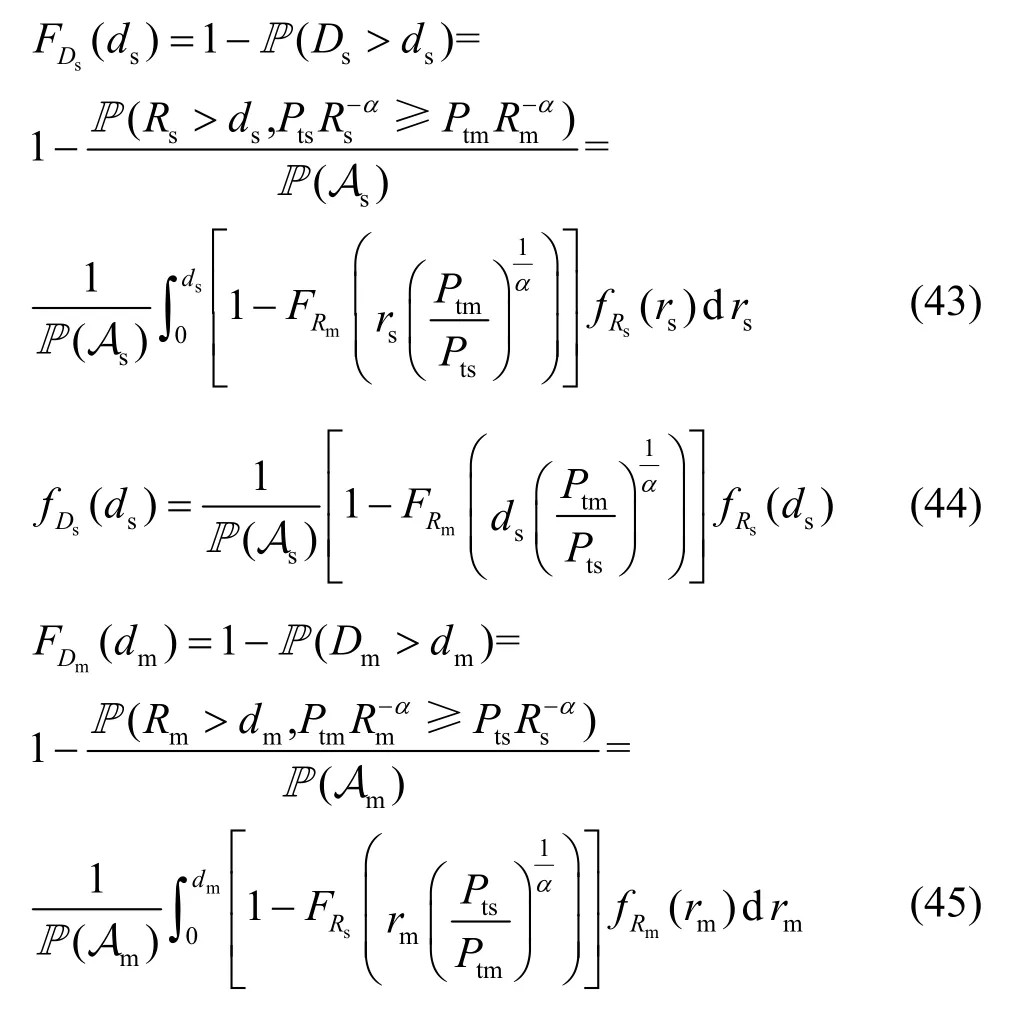
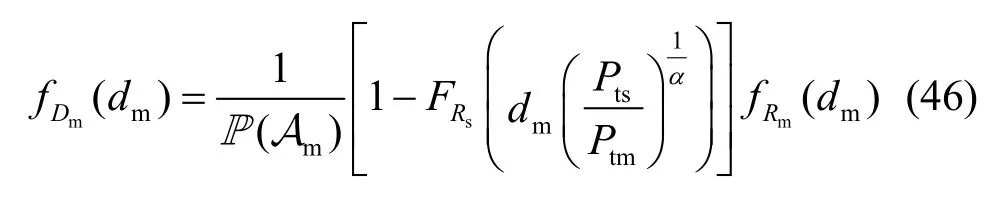
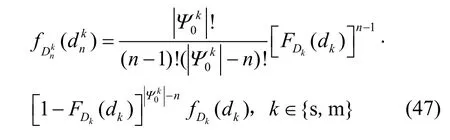
4.4 功率分配方案

根据式(7)、式(8)、式(41)和式(42)，每个NOMA簇的用户数量与BS密度、BS发射功率和Matern簇半径等参数密切相关，并随之动态变化。而现有关于NOMA的功率分配算法研究大多数都是基于固定用户数量进行优化，故与文献[14]类似，本文采用固定功率分配方案。具体表述为，针对每个NOMA簇，保证分配给的功率为

综上所述，将4.1节～4.4节的分析结果代入式(21)，即可获得各类用户的覆盖概率。

5 数值仿真分析

根据3GPP规范中基站设定的发射功率和相关文献[11,23]，本节利用仿真工具，根据第2节所述系统模型，对基于MCP的双层NOMA-HetNet模型中相关理论推导结果进行了仿真验证和分析，主要仿真参数如表1所示。

表1 仿真参数

图5和图6分别为关联概率和NOMA簇内平均用户数量随簇半径R和MBSs密度λm变化的仿真结果。可以看出，随着R和λm的增大，用户关联MBS的概率增大，关联SBS的概率减小，进而影响MBS和SBS服务的NOMA簇大小。原因在于，式(3)中随簇半径R增大而减小，会使式(41)中随之减小，从而引起式(7)中关联SBS的平均UE数量减小；另一方面，UE与SBS的相对密度保持不变时，λm的增大，会使UE在距离MBS更近的地方出现的概率增大，从而使式(42)中增大，引起式(8)中关联MBS的平均UE数量减小。

图5 关联概率

图6 NOMA簇内平均用户数量

图7～图10给出了不同簇半径大小下，UE与BS间服务距离的总体分布特性。仿真参数为λm=1km-2,λs=5km-2。图7和图8分别描述了UE关联SBS时，服务距离Ds的PDF和CDF；图9和图10分别描述了UE关联MBS时，服务距离Dm的PDF和CDF。根据图8和图10的仿真结果，Ds和Dm的理论CDF曲线和实际结果几乎重合，验证了理论推导结果的正确性。图7和图9表明，服务距离Ds的概率密度随着簇半径R的增大而变小，而在Dm较小时，服务距离Dm的概率密度随着簇半径R的增大而减小，在Dm很大时，Dm的概率密度随着簇半径R的增大而增大；在同一簇半径R下，距离越大，Ds的概率密度越大，而Dm的概率密度先增大后减小。原因在于，R的增加对和几乎无影响，但会使减小，导致子过程点变得更稀疏，从而影响

图7 Ds的PDF

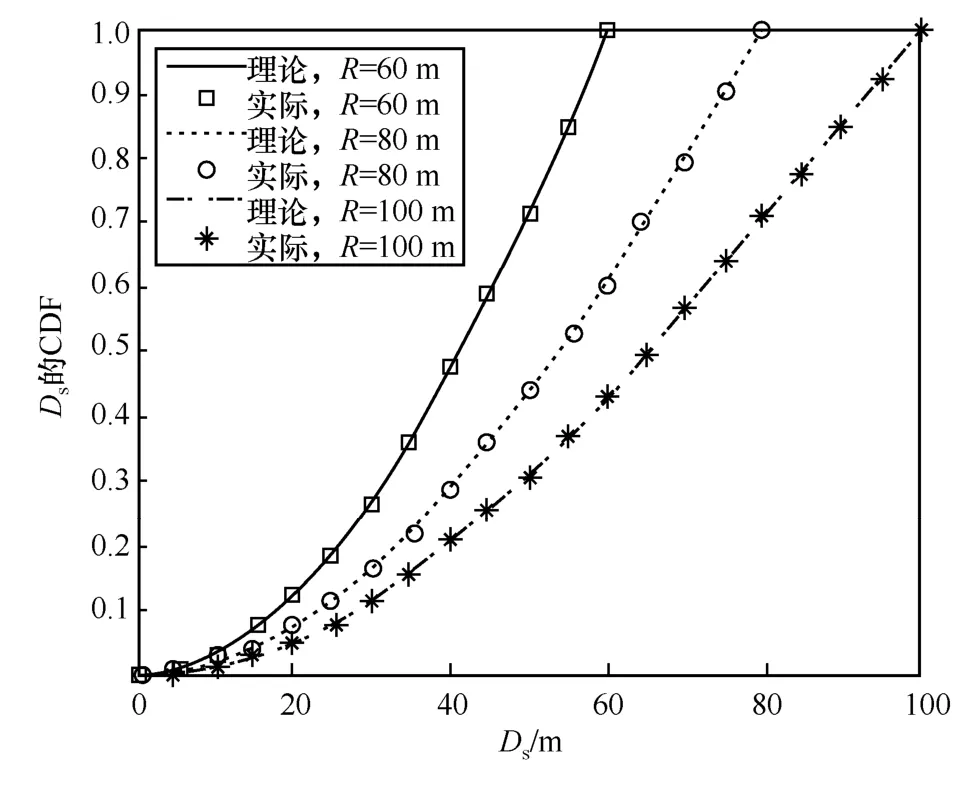
图8 Ds的CDF

根据图6，当λm=1km-2、λs=5km-2、簇半径R=100m 时，关联SBS和MBS的UE数量分别为3和5。图11和图12分别描述了SBS和MBS所服务的NOMA簇内各个用户与基站间服务距离的分布特性（即式(47)中的并与各自的母体分布曲线（式(44)中的和式(46)中的进行了比较。由仿真结果可知，距离BS越近的用户（根据2.2节的假设，n越小，UE距离BS越近），在短距离范围内的概率密度越大，在长距离范围内的概率密度越小；各个用户的服务距离分布曲线与母体的分布曲线走势相似，符合顺序统计量的性质，证明了理论推导结果的正确性。

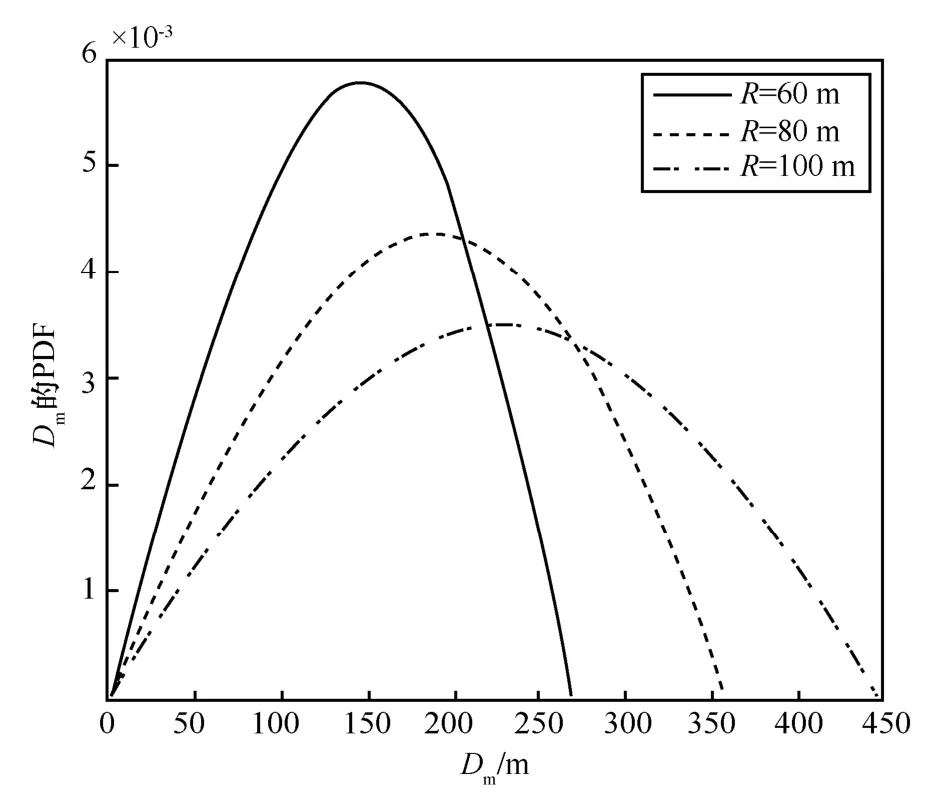
图9 Dm的PDF

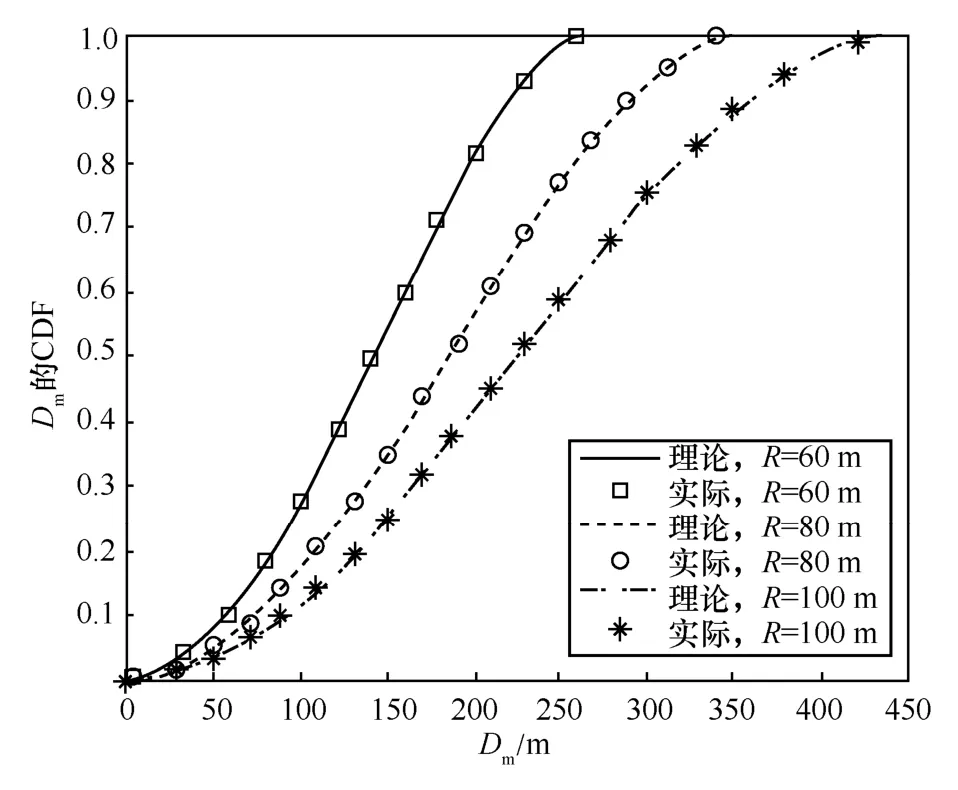
图10 Dm的CDF

图13和图14分别为由SBS和MBS服务的NOMA簇内用户的覆盖概率随SINR门限变化的关系曲线；同时将文献[14]中完美SIC方案与本文不完美SIC解码方案下的覆盖概率进行了对比。仿真参数为λm=1km-2，λs=5km-2，R=100m。结果表明，距离BS越近的用户覆盖概率越大。原因在于，根据式(9)～式(14)，针对同一NOMA簇中的用户，相同，而n越小，越小，即越接近BS的用户，受干扰影响更小，信道质量更好，故覆盖概率越大；同时，NOMA簇的规模越小，簇内各用户的覆盖性能越好，这是因为簇的规模越小，簇内干扰越小，进行SIC解码时受到的限制越小（在本文功率分配方案下，式(16)中小于解码门限的概率越小）。另一方面，与文献[14]中完美SIC情形相比，在本文考虑的不完美SIC情形中，当NOMA簇内最弱的UE不能成功解码时，簇内其他UE在同一SINR门限下也不能成功解码，尽管其覆盖概率有所削弱，同时更新SINR上限值方面增加了少量复杂度，但更符合实际。

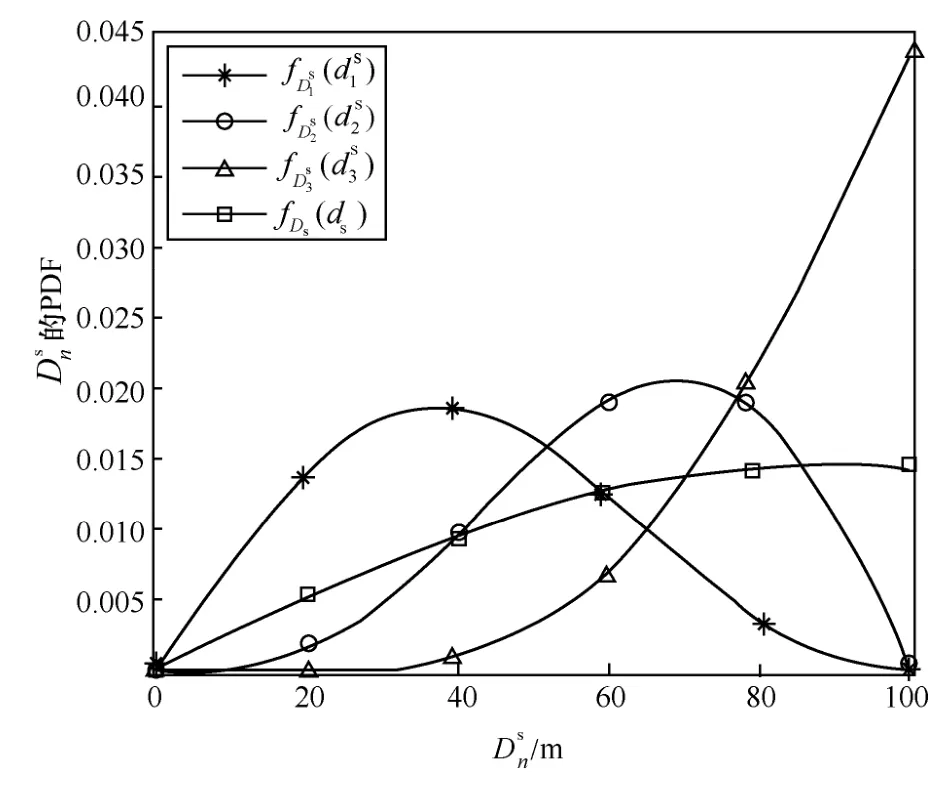
图11 的PDF

图13 SBS服务的NOMA簇内用户覆盖概率

图14 MBS服务的NOMA簇内用户覆盖概率

图15为系统平均覆盖概率、关联SBS和MBS的UE的平均覆盖概率（即式(17)～式(19)中的Prc、随SINR门限的变化曲线。可以看出，在较低SINR门限（小于-3 dB）下，簇内的用户均能成功解码时，2种不同类型NOMA簇的平均覆盖概率差别较小，在满足一定覆盖率的同时保证了用户的公平性；而在较高SINR门限（大于-3 dB）下，MBS服务的簇内部分用户不能成功解码，导致关联MBS的UE的平均覆盖概率迅速下降，大幅降低了系统平均覆盖概率。同时，与文献[14]中完美SIC情形相比，在本文中的不完美SIC情形中，由于UE的SINR上限值变化，覆盖性能不可避免地有所削弱，但更符合实际情况。

图16和图17分别为SIC后，干扰残余因子ε对由SBS和MBS服务的NOMA簇内用户的覆盖概率的影响。仿真结果表明，较低的干扰残余（例如ε=0.1）对覆盖性能影响较小，但当干扰残余率较大时（例如ε=0.5），对覆盖概率的恶性影响将会显著加深。这是因为干扰残余因子ε的增大，会增大簇内干扰式(10)中的，使越靠后解码的UE（距离BS越近的UE）受到更严重的簇内干扰影响，进而减小SINR，导致覆盖概率降低。

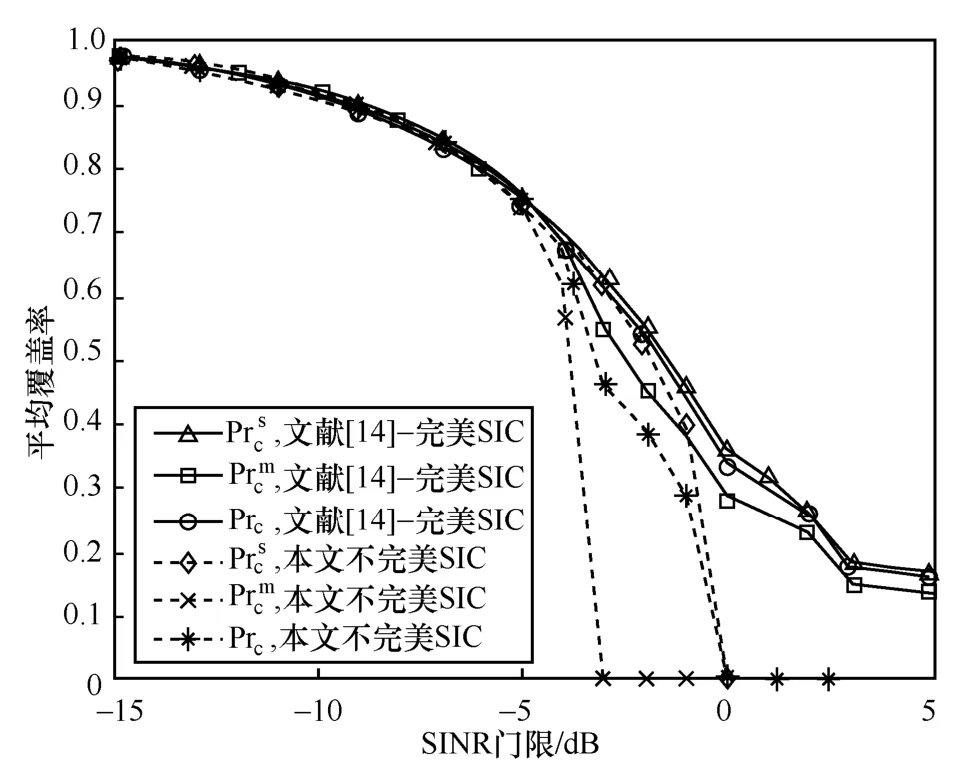
图15 平均覆盖概率

图16 干扰残余因子对SBS的用户覆盖概率的影响

6 结束语

考虑用户与小基站的相关性和现实网络中的随机性和不规则性，融入NOMA技术，建立了一种基于MCP的新型NOMA-HetNet模型，进而借助随机几何理论和顺序统计量等数学工具，推导了该模型下服务距离和覆盖概率的理论表达式；通过数值仿真，分析了簇半径、基站密度和SIC干扰残余因子对服务距离和覆盖概率的影响，验证了理论推导的正确性。结果表明，通过设置合适的系统参数，基于MCP的新型NOMA-HetNet模型能在保证一定覆盖概率的同时，进一步提升系统服务的UEs数量，从而给未来NOMA-HetNet的部署提供了一定理论支撑。

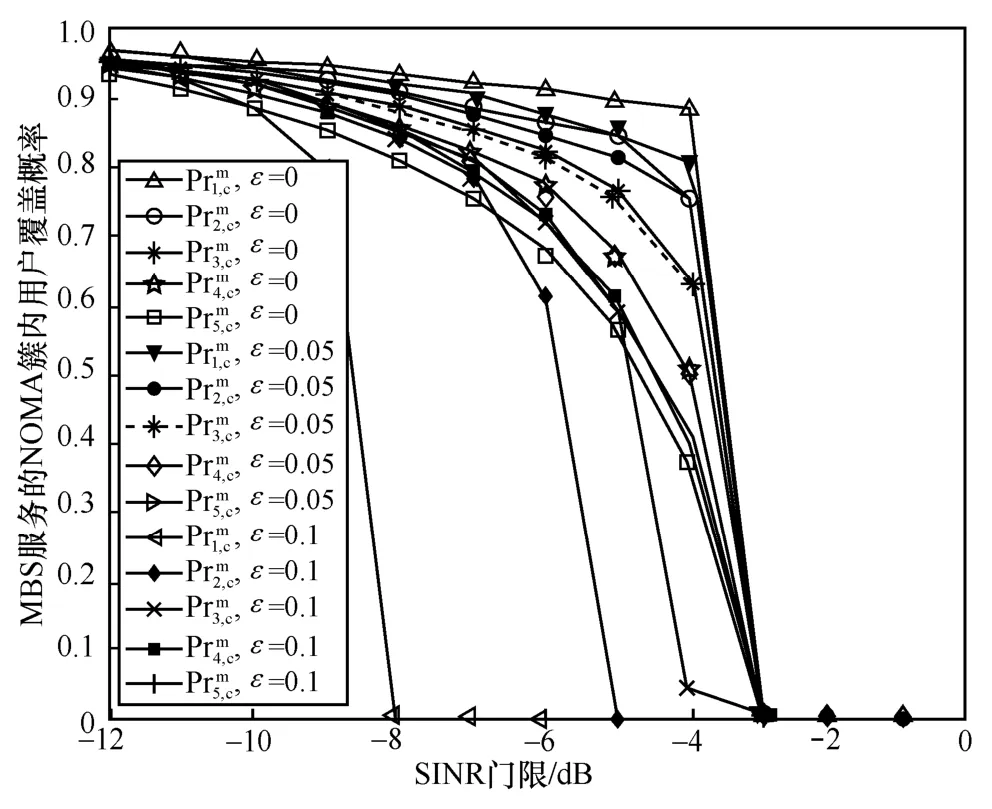
图17 干扰残余因子对MBS的用户覆盖概率的影响