基于贝叶斯攻击图的网络入侵意图分析模型
2020-10-11罗智勇杨旭刘嘉辉许瑞
罗智勇,杨旭,刘嘉辉,许瑞
(哈尔滨理工大学计算机科学与技术学院,黑龙江 哈尔滨 150080)
1 引言
信息技术的飞速发展,使现代社会对互联网更加依赖,但是也使网络攻击更加复杂,更具有危害性。传统的入侵检测系统(IDS,intrusion detection system)只能在攻击发生后对节点漏洞间的依赖关系进行分析,进而监控攻击行为,这属于被动防御[1]。因此IDS无法对网络进行系统的安全风险评估,针对未知网络中潜在的风险,如轨迹隐蔽的多部攻击进行有效防护[2]。20世纪90年代,Phillips等[3]最早提出了攻击图的概念,利用受攻击节点的配置信息、节点间的因果关系和攻击者的能力生成攻击图,并将其应用于对网络脆弱性的分析。攻击图是一种由顶点和有向边组成的有向图,根据模型的不同,顶点可以表示主机、服务、漏洞、权限、网络安全状态的要素,有向边表示攻击者攻击路径的攻击顺序[4]。攻击图可以直观地图形化地展示攻击行为的细节,如目标网络、漏洞、攻击路径等[5],为预测攻击者的攻击意图和后续攻击行为提供支撑,便于管理员及时应对突发的网络入侵事件[6]。
胡浩等[7]提出的状态转移概率归一化算法将攻击图映射为吸收马尔可夫链,利用马尔可夫链的马尔可性和漏洞评分系统计算状态转移概率,对各个节点的可能访问次数和通向目标节点的路径长度做出预测。雷程等[8]为了对网络中的移动目标进行防御并计算出成本和收益,利用攻击图建立分层网络资源图,结合变点检测方法,提出了一种基于变点检测的网络移动目标防御效能评估方法,有效提高了网络资源图的构建效率。Hu等[9]利用不同维度的告警信息和实时攻击行为,计算出漏洞利用率,评估攻击者的能力,提出基于动态贝叶斯攻击图的威胁预测算法,实现量化网络威胁和遭受持续攻击的风险。王辉等[10]利用贝叶斯理论计算各节点的可达概率,描述单步攻击发生概率,动态预测网络中潜在的风险,结合攻击图提出一种基于改进型攻击图的入侵预测算法,简化告警证据和攻击行为的联系,提高预测的准确性。秦虎等[11]用矩阵描述主机间的关系和状态转移过程中攻击者权限的提升,提出一种基于权限提升矩阵的攻击图生成方法,该方法对于复杂网络的攻击图生成问题具有更好的适应性。
上述研究基于攻击图建立了不同的网络安全风险评估模型,但对于原子攻击概率的评估指标过于单一,无法真实地反映攻击者对目标网络和攻击路径选择的可能性,且没有针对攻击者的意图量化网络节点的风险情况。本文基于贝叶斯攻击图建立了一种动态网络入侵意图分析模型,主要工作和创新如下。
1)考虑到影响攻击者攻击行为的复杂因素,从漏洞价值、攻击成本和攻击收益3个指标对原子攻击概率进行计算,更真实地反映了漏洞在实际网络中被利用的情况。
2)将贝叶斯信念网络和攻击图结合,针对攻击者的攻击意图,建立动态风险评估模型应对安全要素不断变化的复杂网络,提高了风险评估的准确性。
3)生成攻击路径并计算出路径总体可达概率,实现对攻击路径的预测,避免了单个网络节点漏洞对路径选择的影响,提高了预测的准确性。
2 贝叶斯攻击图建立
攻击图可以分为状态攻击图和属性攻击图。状态攻击图中顶点表示网络状态信息,边表示状态的迁移方向和过程,但是状态攻击图无法应对快速增长的状态节点,并且结构上不够直观,因此不适用于大规模网络。属性攻击图中每个属性顶点代表一个独立的安全要素,避免了状态攻击图的状态爆炸问题[12],因此,属性攻击图对复杂的大规模网络具有更好的适应性。为了计算出攻击图中顶点到达概率和可能的攻击路径,本文利用贝叶斯信念网络来描述攻击间的因果关系,结合攻击图的图形化结构,生成贝叶斯攻击图对目标网络进行风险评估。
2.1 贝叶斯攻击图定义
贝叶斯攻击图(BAG,Bayesian attack graph)是一个有向无环图,可以表示为BAG=(S,A,E,R,P),具体定义如下。
1)S为属性节点集合,分为三类,即S=Sstart∪Stransition∪Starget,其中,Sstart为网络攻击的发起节点,Stransition为攻击行为的过程节点,Starget为攻击者的目标节点。其中,Si={0,1},1表示攻击者已经成功利用该属性节点漏洞占用该节点,0表示该节点未被占用。
2)A={Ai|i=1,2,…,n}为原子攻击集合,表示攻击者对节点漏洞的攻击行为,即属性节点的迁移方式,可表示为Ai:Spre→Snext。
3)E={Ei|i=1,2,…,n}为攻击图中的有向边集合,表示属性节点间攻击行为的因果关系,其中(Spre,Snext)∈Ei表示从Spre攻击Snext的一条有向边。
4)R表示父子属性节点间的关系,可用二元组
5)P为攻击图中属性节点的可达概率;P1为攻击图中节点属性的静态可达概率;P2为攻击图中节点属性的动态可达概率。
2.2 贝叶斯攻击图结构建立
贝叶斯攻击图的结构与一般攻击图的结构类似,本文采用模型化方法生成攻击图的主要结构,示例如图1所示。
图1中,S0为攻击的发起节点,S1和S2为过程属性节点,S3和S4为攻击者的目标网络节点,A1、A2、A3、A4、A5、A6为原子攻击。AND表示原子攻击A5和A6到达S4的攻击策略全部为真,攻击才可实现;OR表示原子攻击A3和A4到达S3的攻击策略只要有一个为真,攻击就可实现,即图例所示2条攻击路径完成其中任意一个,就可完成对目标节点S3的攻击。

图1 贝叶斯攻击图示例
2.3 贝叶斯攻击图量化
2.3.1漏洞价值
漏洞价值与该属性节点漏洞被利用的难易程度和影响大小有关,一般采用美国国家通用漏洞数据库(NVD,national vulnerability database)提供的通用漏洞评分系统(CVSS,common vulnerability scoring system)[13]进行量化。CVSS能提供完整的评分参数和开放的评分框架,将动态评估和属性节点间漏洞的依赖关系结合,量化漏洞被利用的难易程度。本文根据CVSS量化标准,从可利用性、影响度和范围3个指标进行量化,其中,可利用性包括攻击途径(AV,access vector)、攻击复杂度(AC,access complexity)、权限要求(PR,privileges required)和用户验证(UI,user interaction);影响度包括机密性(C,confidentiality)、完整性(I,integrity)和可用性(A,availability);范围表示漏洞的影响是否会扩大到其他组件。CVSS指标评分如表1所示。
攻击者攻击漏洞时会依据漏洞的可利用性和影响度两方面来考虑漏洞价值,所以为了量化漏洞价值,首先计算出代表漏洞价值的漏洞评分Score,其计算式为

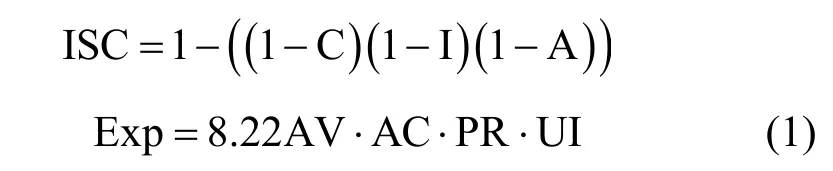
其中,Impact表示漏洞影响因子,Exp表示漏洞利用因子,ISC表示中间变量,常数10表示Score的最大取值为10,其他常系数取值由CVSS根据安全策略进行设置。
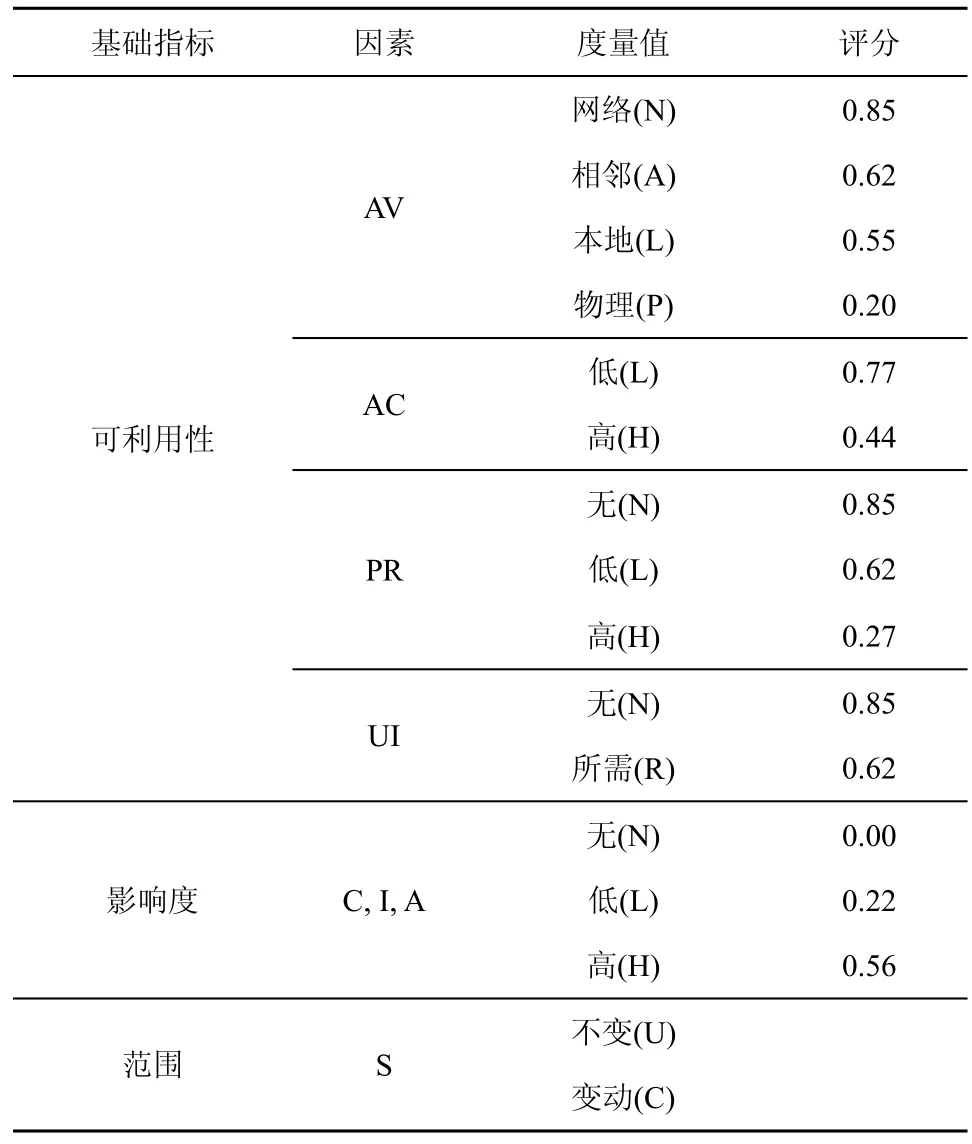
表1 CVSS指标评分
定义1漏洞价值表示攻击者利用某漏洞的可能性对于漏洞vi,用value(vi)表示其漏洞价值,大小与漏洞评分有关。由于CVSS标准的漏洞评分取值范围是[0,10],为了方便后续概率的计算,value(vi)的计算式为

2.3.2攻击成本与收益
攻击者对某网络节点发起攻击时,不仅会考虑该节点漏洞的价值,还会考虑攻击该节点的成本与攻击完成后所带来的收益。攻击的成本与收益不会影响节点间原本的状态转移性质,但是会影响攻击者对攻击节点的选择,一个理性的攻击者会选择攻击成本低、收益高的节点。本文参考马春光等[14]的方法对攻击成本与收益进行定义。
定义2攻击者在发起一次攻击行为时,会投入人力资源、物力资源、攻击代价等必要的成本,对于原子攻击Ai,用cost(Ai)表示该次攻击所消耗的成本,即攻击成本。
本文从攻击代码信息(SI,shellcode information)、攻击代码对应平台(SP,shellcode platform)、攻击操作需求(Or,operation requirement)、信息收集需求(IR,information requirement)4个指标对攻击成本进行评估,具体评分如表2所示。

表2 攻击成本评分指标
利用SI、SP、Or、IR这4个指标的评分可以对攻击成本进行量化,计算式为

定义3对于某一原子攻击Ai,攻击者通过该攻击完成对节点的攻击时,所能获得的收益称为攻击收益,用income(Ai)表示,具体评分如表3所示。

表3 攻击收益评分指标
攻击完成后的属性节点最终状态价值等同于该次攻击的收益income(Ai),本文给出的每个最终状态价值评分是一个范围值,在不同实际运行的网络环境中,具体的值可由管理员根据经验来赋值。
2.3.3原子攻击概率
综合对节点漏洞价值、攻击成本与收益的量化,可以计算出攻击者在当前属性节点对其子节点发起攻击的概率,即某一原子攻击的概率,取值范围为[0,1]。当攻击概率为0时表示该次攻击对于攻击者无收益,攻击者不会发动攻击;攻击概率为1时表示该次攻击可获得的收益远远大于成本,攻击者必定会发起攻击。
定义4攻击者通过漏洞vi完成一次原子攻击Aj的概率称为原子攻击概率,用P(Aj)表示,计算式为

2.3.4条件概率
在攻击图中,属性节点并非是独立的,能否被占用还受其父节点的影响,所以需要计算该节点在整个攻击图中的条件概率。
定义5条件概率表示某属性节点在其父节点的影响下被攻击的可能性,对于属性节点Sj,条件概率用P(Sj|Par(Sj))表示,其中Par(Sj)表示Sj的父节点集合。根据dj的不同,条件概率的计算式分别如式(5)和式(6)所示。
1)当dj=AND时,有
2)当dj=OR时,有

2.3.5静态可达概率
利用贝叶斯攻击图中全部属性节点的条件概率,可计算出每个节点的可达概率,即静态可达概率。静态可达概率可以对网络风险进行静态评估,展示网络的静态风险情况。
定义6静态可达概率表示静态网络中各个属性节点的可达概率,是当前节点与其祖先节点的联合条件概率,即对于Sj∈Stransition∪Starget,用P1(Sj)表示该节点的静态可达概率,计算式为
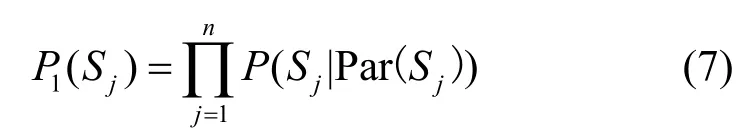
在图1中,属性节点S1、S2的静态可达概率由其条件概率结合S0静态可达概率计算得出。属性节点S3的静态可达概率同样依赖S1、S2的静态可达概率,具体如图2所示。

图2 贝叶斯攻击图漏洞利用概率
S1、S2、S3的静态可达概率为

2.3.6动态可达概率
网络并非是静态的,任何网络安全要素的变化都会影响到静态可达概率,当攻击者的攻击意图已知(即Starget=1)时,整个攻击图中属性节点的可达概率都可能随之发生改变,所以为了针对攻击者的意图量化网络风险,需要结合已知目标属性节点来更新其他节点的可达概率。
定义7将贝叶斯攻击图中属性节点集合S={Si|i=1,2,…,n}分为目标节点集合Supdate={Sj∈S|Sj=0}和需要更新的节点集合Starget=S-Supdate。动态可达概率表示已知目标节点为Sa(Sa∈Starget)后,对更新集中节点Sb(Sb∈Supdate)的可达概率进行动态更新后的概率,用P2(Sb|Starget)表示,计算式为

在图1中,假设已知攻击者的目标属性节点为S3,则属性节点S2的动态可达概率为
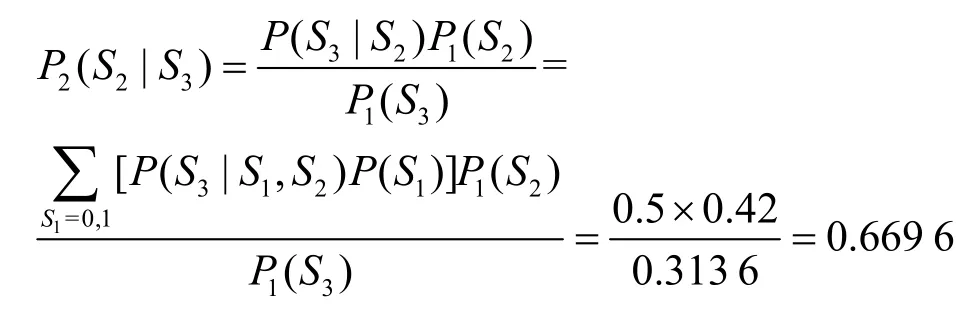
3 贝叶斯攻击图风险分析方法
3.1 静态风险评估
计算出属性节点的条件概率和静态可达概率后,可在原始攻击图的基础上构建静态风险评估模型,静态风险评估可以评估网络中的潜在风险,构建算法如算法1所示。

3.2 动态风险评估
现实的复杂网络中,网络安全要素会随着网络的运行不断发生变化,在知道攻击者的攻击目标时,静态风险评估的准确率会降低。因此,必须结合根据贝叶斯理论计算出的动态可达概率不断更新属性节点的可达概率,构建动态风险评估模型。构建算法如算法2所示。


3.3 攻击路径生成
对网络进行入侵风险评估时,需要针对攻击者的意图预测出攻击者可能发起攻击的攻击路径。依据3.2节和3.3节中的攻击图算法,以目标节点为起点,自下向上查找,得到可对此目标节点发起攻击的攻击路径。需要注意的是,对于某一目标节点Si,如果其有3个父节点且父子间得依赖关系是OR时,需要再生成2条攻击路径来容纳另外2个父节点,即通向该节点的路径至少有3个。
定义8攻击路径表示在生成的贝叶斯攻击图中,入侵者可由初始属性节点Sstart沿着一组属性节点入侵至目标节点Starget,则该组节点组成的路径为贝叶斯攻击图的一条攻击路径APi,攻击图中的攻击路径集合记为Attack Path,具体算法如算法3所示。


定义9为了比较不同路径被攻击者攻击的概率,将某条路径上所有节点的可达概率进行乘积运算,其积为该路径的总体可达概率,即对于APi,总体可达概率计算式为

4 实验分析与优化评估
4.1 实验建立
为了验证基于贝叶斯攻击图的入侵意图分析模型的准确率,本文建立了如图3所示的网络拓扑结构。该结构主要包含D1域、D2域、D3域和DMZ域,通过安装防火墙划分网络区域,并制定子网间的通信规则,保证外部访问无法到达内网区域。具体访问规则介绍如下。

图3 实验网络拓扑结构
1)D1域内只有主机H6可以访问SQL数据库。
2)D2域内只有主机H9可以访问SQL数据库。
3)D1域和D2域的主机可以与DMZ域内的服务器相互访问。
4)D1域访问D2域只能通过主机H6访问主机H7。
5)域内主机可以相互访问,禁止其他跨域访问。
4.2 攻击图生成
利用OVAL漏洞扫描器对实验网络进行扫描,得到各主机与服务器存在的漏洞信息,并利用式(1)和式(2)计算出漏洞价值,如表4所示。

表4 漏洞信息和漏洞价值
在图3的实验网络中,SQL数据库服务器存在着重要数据,可以将H12看作攻击者的入侵意图,利用扫描到的漏洞信息、漏洞间的关系、主机与服务器信息、网络配置等数据生成并输出图形化的攻击图,如图4所示。
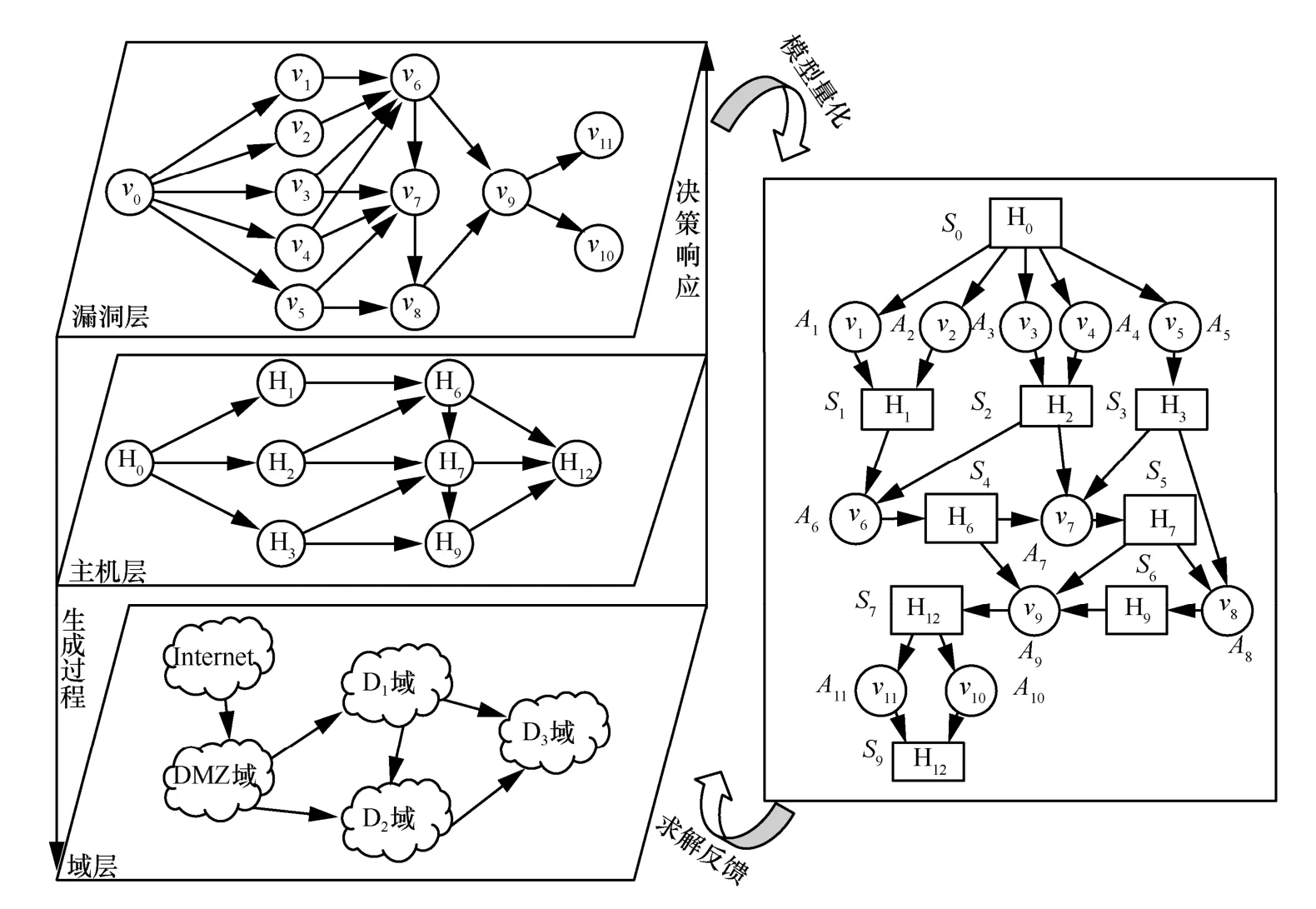
图4 实验环境下的攻击图
图4所示的攻击图中,属性节点表示主机信息或者漏洞信息,原子攻击表示属性节点状态迁移的方式。当某一节点拥有多个父节点时,父子节点间的关系全为OR,即dj=OR。
4.3 风险评估
为了计算出不同原子攻击的概率,首先要计算出对应的攻击成本。根据表2的评分标准,利用式(3)可以计算出攻击图中每次原子攻击的消耗成本,如图5所示。

图5 原子攻击成本
将计算出的攻击成本与表4所示漏洞价值以及实验攻击图中原子攻击的收益代入式(4),计算出各个原子攻击概率,如图6所示。

图6 原子攻击概率
结合图6中获得的攻击图上每个原子攻击的概率,计算出每个属性节点的条件概率,再利用条件概率联合攻击轨迹依据算法1得出各个节点的静态可达概率,对实验网络进行静态风险评估。其中,节点S0的静态可达概率初始化为P(S0)=0.7。确定攻击目标为S8后,按照3.3节提出的算法2和式(8)对攻击图中各个属性节点的可达概率进行更新,得到动态风险评估攻击图中各个节点的动态可达概率。其中,每个节点的静态可达概率和动态可达概率分布如图7所示。
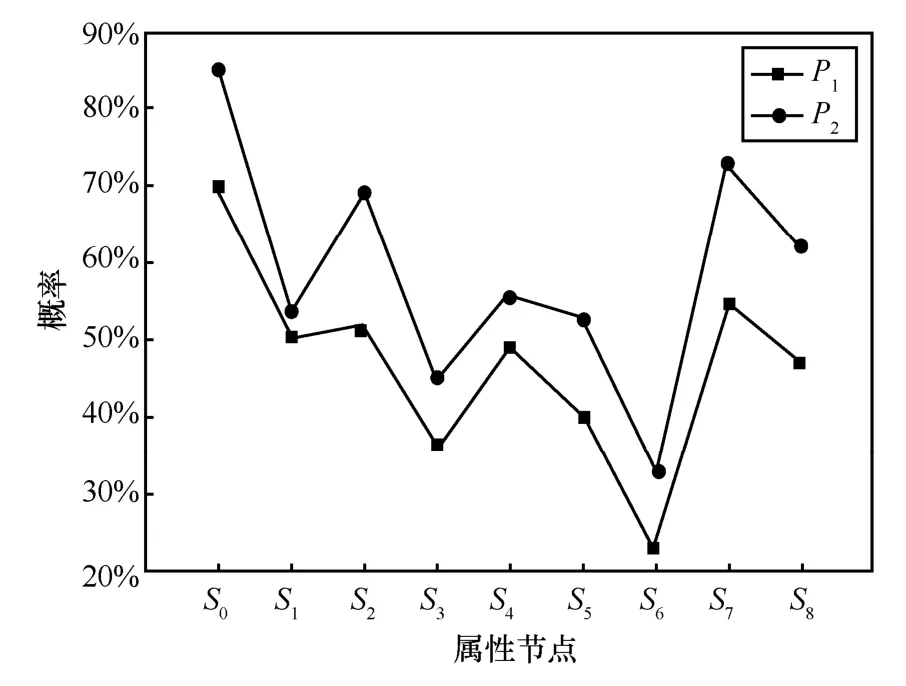
图7 属性节点可达概率
在知道攻击者的目标节点后,实验网络中各个属性节点的可达概率都呈现上升趋势,即网络的入侵风险有明显的提升,目标节点S8的可达概率也由47%上升到62%,中间属性节点S2、S7的被入侵风险最高,需要采取措施更新主机补丁。所以在真实的网络环境中,动态评估方法对网络风险评估的准确性明显高于静态评估,可以为管理员进行网络风险管理提供良好的支撑。
4.4 攻击路径
利用算法3对图4所示的攻击图进行查找,得到7条攻击路径,如表5所示。
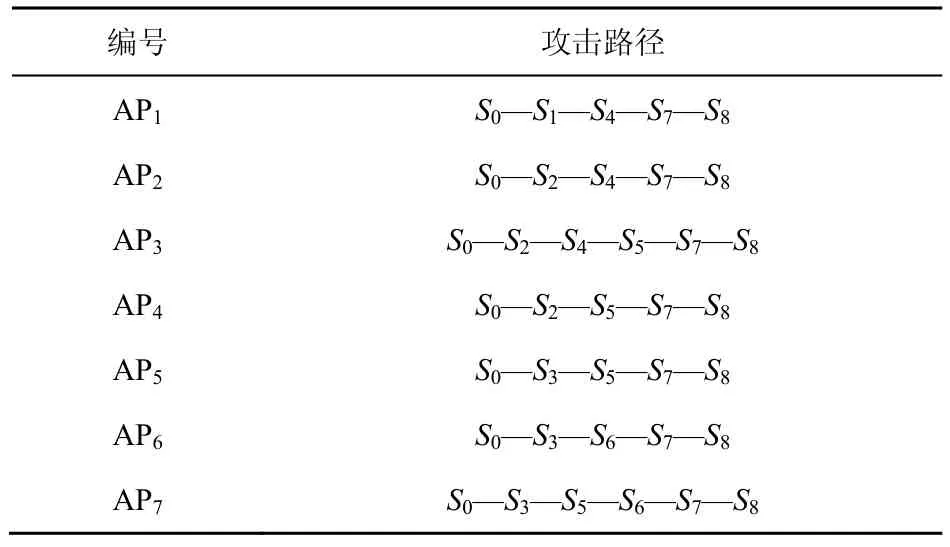
表5 攻击路径
利用式(9)计算出每条路径在静态攻击图和动态攻击图中的总体可达概率,如图8所示。从图8可以看到,无论在静态模型还是动态模型中,攻击路径AP2被入侵的风险最高。当明确攻击者的目标后,各条路径的总体可达概率均有所提高,特别是攻击路径AP4,通过该条路径入侵节点S8的风险已经接近AP2。数据表明,在确定攻击者的意图后,网络风险发生了变化,动态风险评估能够更加准确地分析网络风险。

图8 攻击路径总体可达概率
4.5 方法对比
攻击图中各属性节点的可达概率是对网络安全风险评估的主要指标,攻击路径的预测可以为网络管理员提供入侵防御依据。为了验证本文模型的优越性,在同样的网络环境下,分别给出文献[15]方法、文献[16]方法与本文方法的实验数据对比。
图9给出了同样在图5所示的网络环境下,3种方法中不同属性节点的动态可达概率分布。文献[15]和文献[16]的评估模型也是采用贝叶斯信念网络来描述网络攻击行为间的因果关系,但是由于其对漏洞的评估指标过于单一,且没有考虑到攻击的成本与收益,导致二者的漏洞利用率并没有真实地反映网络中漏洞的被利用情况。由图9可以看出,本文评估模型的准确性明显优于二者,因为本文从多个指标对原子攻击概率进行计算,评估更加准确。
预测攻击者实施攻击行为的攻击路径选择是对网络风险的进一步分析。本文分别利用3种方法进行攻击路径的预测,在相同网络环境下,预测攻击者对目标节点所选择的攻击路径。图10展示了3种方法分别在静态网络和动态网络下对目标节点S8预测被攻击路径的总体可达概率对比。
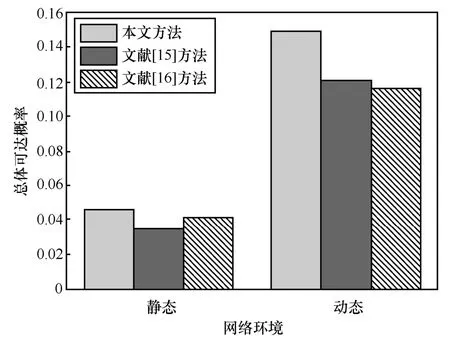
图10 预测路径可达概率对比
虽然3种方法都对攻击者可能利用的攻击路径进行了预测,但是很明显,本文方法预测的路径总体可达概率高于另外二者。这是因为,首先,二者对于原子攻击概率的量化过于单一,导致属性节点的可达概率计算并不准确。其次,二者预测攻击路径的方法是从目标节点开始,不断向上查找可达概率最大的属性节点,但是忽略了单个节点对攻击路径预测的影响。例如,通向某目标节点有2条攻击路径,其中各属性节点可达概率分别是(0.9,0.9,0.5,0.4,0.3)和(0.7,0.7,0.6,0.4,0.3),如果按照文献[15]和文献[16]方法预测的结果应该为后者,但是从整体性上考虑,攻击者对攻击路径的选择应该更倾向于前者。
5 结束语
为了保护重要的网络节点,针对攻击意图量化网络安全风险,给网络安全管理员提供安全策略支撑,提出了一种基于贝叶斯攻击图的网络入侵意图分析方法。首先,利用漏洞价值、攻击成本和收益3个评估指标计算出原子攻击概率,通过原子攻击概率得到静态可达概率和动态可达概率量化攻击图,构建基于入侵意图的风险分析模型;其次,利用构建的风险分析模型计算出每条攻击路径总体可达概率,预测可能的攻击路径;最后,从属性节点的可达概率和预测路径的总体可达概率2个方面和其他文献的评估方法进行对比,验证本文方法的优越性。在实际网络中,漏洞间的关联性也会影响原子攻击的概率,下一步将对此展开研究,优化网络入侵风险评估模型。
