基于Stackelberg博弈的双目标WOA频谱共享算法

张力，廖天，何业军

（深圳大学电子与信息工程学院，广东 深圳 518060）

1 引言

人们对通信的需求从早期的文字通信演变为当今的视频通信[1]。随着通信需求的不断增加，有限的频谱资源很难满足人们的需求[2]，主要表现为现有频谱资源调度和分配的不合理[3]。

现有的频谱资源共享方式[4]无法最大程度地保证通信服务质量，原因是在解决认知用户和授权用户之间频谱资源的共享问题及认知用户之间频谱资源的竞争问题时没有考虑授权用户和认知用户的通信质量，也没有考虑系统中所有用户的公平度，对于系统中授权用户和认知用户之间的竞争也没有考虑。而解决这类问题的主要方法就是博弈论[5]，通过博弈论的相关原理有效地解决授权用户和认知用户之间的竞争关系，使最终的调度方案达到纳什均衡[6]。

Niyato等[7]对合作博弈方式和非合作博弈方式进行了对比分析，对这2种博弈方式的应用场合、优缺点及构架进行了介绍，并给出了不同场合选择博弈方式的依据，为博弈论的进一步应用奠定了基础，但只停留在理论分析阶段。Kim 等[8]提出了一种多主多从结构的Stackelberg博弈理论，并从理论上论证了该方法通过多次迭代和反馈之后可以搜索到最优的纳什均衡，但复杂的反馈决策限制了应用。Nguyen等[9]提出一种基于预测和感知的频谱共享方法，该方法将资源块的时间结构分为频谱预测、频谱感知和数据传输，改善了部分性能但未在博弈理论进一步研究。Zhu等[10]针对宏用户提供更多访问频谱的机会，设计了一种激励机制，该机制使用一种分层的动态博弈框架，下层建立演化博弈模型，上层建立Stackelberg差分博弈模型，然而该分层博弈架构将引入层间干扰问题，但文中并未考虑。张婷等[11]设计演化博弈算子，建立分式规划机制的次用户效用函数，实现了能效最优的资源分配，但该方法仅考虑能效而未考虑如频谱利用率等问题。Vidal等[12]基于博弈论研究在不干扰主用户的条件下让次用户使用频谱，而该方法提高的频谱利用率有限。Yang等[13]基于Stackelberg博弈调整使资源分配最大化效用，降低能耗，该方法在其他资源分配模型中有待进一步验证。Al-Talabani等[14]研究基于Stackelberg博弈让主网络和次节点共享频谱资源，并加入噪声提高认知无线电网络传输保密性。韩松等[15]考虑主用户二次边际成本，设计主用户反馈机制和次用户信任机制，以最大化效用和提高频谱利用率，其考虑的主次用户效用函数较为简单。博弈和非博弈集中调度最主要的差异是博弈集中调度的认知用户和授权用户的博弈结果会相互影响，从而不断在博弈策略中选择较优的博弈结果，非博弈集中调度取决于具体的调度参与者，一般不会相互影响。

本文考虑用户的公平度，给出了反映认知用户频谱需求的效益函数，引入了双目标鲸鱼优化算法（WOA,whale optimization algorithm），实现公平有效的频谱分配。本文的贡献如下：1)基于Stackelberg博弈引入双目标WOA，将授权用户和认知用户共同的收益优化分为各自的收益优化过程，设计出一种新的基于Stackelberg博弈的频谱共享调度算法；2)通过加入影响认知用户公平分配频谱的函数到认知用户收益的优化模型中，能实现认知用户较为公平的频谱分配，最终得到授权用户和认知用户的最优频谱分配结果。

本文首先描述双目标WOA；然后建立频谱共享博弈模型，提出了双目标WOA频谱共享算法，并介绍了算法的实现步骤和流程；最后对本文算法进行仿真验证，分析了算法复杂度、仿真时间、系统效用方面等性能。

2 双目标WOA

传统的WOA[16]主要针对单一目标的猎捕，当考虑2个目标猎物时，主要会涉及以下关键因素。

1)每个“猎物群”的“猎物”数量。如果2个“猎物群”中的“猎物”个体数量差异比较大，“猎物”个体是否优先考虑大“猎物群”，以满足“猎物”个体最后的“捕食”需求。

2)距离2个猎物群中心位置的距离。如果“猎物”个体与小数量猎物群的距离远小于与大数量猎物群的距离，是否先考虑捕食小“猎物群”，进而围捕大“猎物群”。

3)约束条件。在何种情况下会形成双目标捕食环境等。

2.1 初始条件

针对初始鲸鱼群个体环绕数量，设置个体数量浮动因子F，群族个体数量Q，环绕“猎物”（“猎物1”和“猎物2”）的初始个体数量表示为

其中，rand()表示(0,1)之间的随机量，Q1与Q2分别表示“猎物1”与“猎物2”初始环绕的捕猎者数量，F表示(0,1)之间的变量。

2.2 距离与权重

距离是优先考虑的因素，当距离优势足够明显时，即d1＞2d2，则不考虑其他因素的影响直接追击“猎物2”，反之亦然，其中d1和d2表示捕猎者分别与“猎物1”“猎物2”的距离。当距离优势不够明显时，则需要考虑目标对于个体的最要性来决定下一时刻的追击目标，可得式(3)。

其中，μi表示猎物个体在整个猎物群体中的权值，i=1,2,…,N。当同时考虑距离与权重时，则每个个体在更新位置前需要做出式(4)所示的判断。

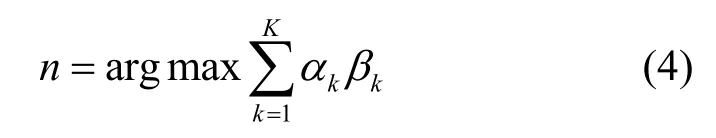
其中，K表示影响目标选择的个数；αk表示各影响因素之间的比重；βk为对应因素的权值；n表示该时刻捕猎的目标，以对下一时刻的位置进行更新。

2.3 收敛速度与精度

在鲸鱼螺旋捕食阶段[16]，根据式(5)进行优化。

其中，X(t+1)为捕猎者的位置向量；t为迭代参数；D′为捕猎者与猎物的距离向量；l为 0～1的随机变量；b为常量；X*(t)为每次迭代捕猎者的局部最优位置向量；γ为更新权值，如式(6)所示。

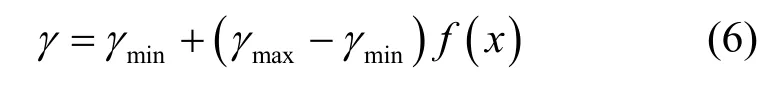
其中，γmin表示最小权值，取值为0.05；γmax表示最大权值，取值为0.95；f(x)表示修正函数，如式(7)所示。

其中，μ表示xi的均值。

2.4 停止条件

选择狩猎目标数量比和单目标权重比的关系为停止条件，对收敛速率和收敛精度都有一定影响。当满足式(8)时，停止对于狩猎目标的选择，以前一时刻的目标为基准，直至完成狩猎目标的捕获。

其中，Q1(t)和Q2(t)分别表示t次迭代时，环绕“猎物1”与“猎物2”鲸鱼的数量。

3 频谱共享博弈模型

当分布式天线系统（DAS,distributed antenna system）和集中式天线系统（CAS,centralized antenna system）通信过程产生相同的吞吐量时，CAS需要更大的发送功率。当DAS和CAS以相同的发送功率进行通信的时候，DAS具有更高的吞吐量[17]。

DAS和CAS能量效率和频谱效率的关系如图1所示。从图1可知，CAS和DAS在频率效率小于2 bit/(s.Hz)时，随着频率效率的增加，两者的能量效率均增加。当频率效率大于2 bit/(s.Hz)时，两者的能量效率逐渐降低并趋于平稳。由于其天线距离用户较远，CAS的大尺度衰落现象较为严重，因此能量效率较低。由于DAS的天线随机分布在小区的不同位置，天线距离用户较近，因此大尺度衰落现象较轻，能量效率较高。由图1还可知，DAS的理论最小值的能量效率也大于CAS，因此本文在DAS的基础上进行研究。

图1 DAS与CAS能量效率与频谱效率关系

本文频谱共享的认知无线电系统如图2所示。假设系统有M个授权用户，一个基站及N个随机分布的天线，其中，N个天线只用于数据信号的发送和接收。所有授权用户将闲置的频谱资源整合为一个共享池，并出售频谱资源给认知用户，从而获得收益。认知用户通过购买共享池的频谱资源来实现信号发送和接收。基站在整个交易环节作为“中间人”，协调授权用户和认知用户间的交易。

图2 网络频谱共享系统

3.1 认知用户的收益建模

假设授权用户的价格策略为P*，认知用户购买的带宽b*，引入式(9)所示的认知用户收益函数[18]。

其中，U(b)为认知用户的收益；b=[b1,...,bi,...,bM]表示M个授权用户给基站的带宽向量；表示认知用户的频谱利用率；ωi表示认知用户所拥有的单位传输速率下所带来的收益；Pi表示授权用户i的频谱价格；b′j表示认知用户j的实际频谱需求；f(·)表示实际的频谱需求函数，其作用是当实际的网络频谱需求改变时，认知用户收益也会改变，所得的均衡点也会发生改变[19-20]，从而使认知用户收益更符合实际频谱需求情况。

假设xij表示天线j的频谱资源是否分配给用户i，如果是，则xij=1，否则xij=0。那么认知用户的收益目标函数为

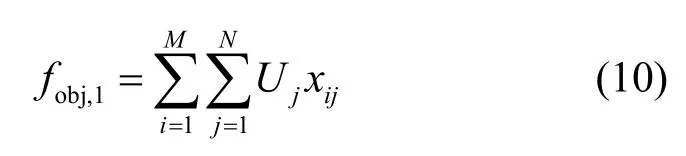
其中，Uj表示认知用户的收益函数，即式(9)的认知用户收益函数。如果某个用户i被分配天线j，那么将产生一个收益Uj。然后通过式(10)计算得到所有认知用户的整体收益值。

3.2 授权用户的收益建模

单个授权用户的收益函数为[21]

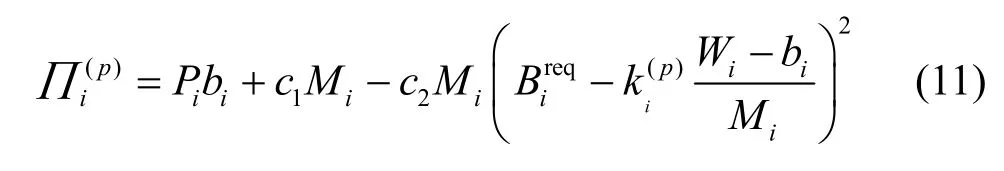
其中，Mi表示授权用户的连接数量；c1表示授权用户收益权值；c2表示授权用户损失权值；表示授权用户系统连接者需求带宽；表示授权用户的频谱利用率；Wi表示授权用户拥有的闲置频谱资源。

当存在多个授权用户时，授权用户的收益函数将有所不同。在Stackelberg博弈中，假设授权用户A的频谱资源价格为pA，授权用户B观测到A的价格后，考虑自身的利益，选择价格pB。在整个过程中，A先有价格，B根据A的价格选择价格，而A无法预先获得B的价格。B的策略定义为SB:QA→QB，其中，QA=(0,∞)表示A的价格区间，QB=(0,∞)表示B的价格区间。因此，其价格向量可以表示为(pA,SB(pA))。同理，对于授权用户C，其价格向量表示为(pA,pB,SC(pA,pB))，其中，pB=SB(pA)。在Stackelberg博弈中，本文以2个授权用户为例，则授权用户收益函数为[21]

那么授权用户的收益目标函数为

其中，Пi(P)为授权用户的收益函数，即式(12)的授权用户收益函数。如果天线j的频谱资源被出售，那么对授权用户将产生一个收益Пi。通过式(13)计算得到所有授权用户的整体收益值。

3.3 认知用户公平度建模

频谱分配的公平度目标函数如式(14)所示。

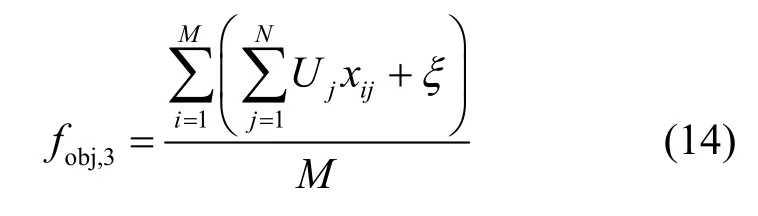
其中，ξ表示一个较小值，一般取0.000 01，以避免出现值为0的情况。

假设某一天线的闲置频谱资源较多，其他天线闲置频谱资源较少，若大多数用户都去抢占该天线资源，将会导致认知用户的个体收益下降，而采用频谱分配的公平度目标函数后，认知用户则选择不同的天线来均衡地购买频谱资源。

3.4 系统效用的建模

认知用户和授权用户的整体收益反映系统效用，设认知用户和授权用户收益归一化值分别为y1和y2，系统效用函数为

其中，λ1和λ2表示加权值，均取值0.5。

3.5 双目标WOA频谱共享算法

在Stackelberg博弈的基础下，本文所采用双目标WOA频谱共享算法的优化模型如式(16)和式(17)所示。

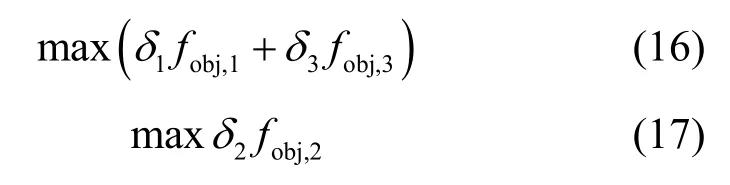
其中，δ1、δ2和δ3表示权值，有δ1+δ2+δ3=1。如果频谱分配结果偏向于认知用户收益，增大δ1；如果频谱分配结果偏向于授权用户收益，增大δ2；如果频谱分配结果偏向于认知用户的公平度，则增大δ3的值。

在优化模型中，为了避免出现不符合实际情况的最优解，使频谱分配更符合实际情况，设置了3个约束条件[17]，如式(18)～式(20)所示。其中，式(18)表示所有认知用户的整体频谱资源需求之和小于所有授权用户的闲置频谱资源；式(19)表示每一个用户只使用某一个授权用户的频谱资源或者不使用任何授权用户的频谱资源；式(20)表示如果认知用户被分配某授权用户的频谱资源，那么xij={1}，否则xij={0}。在该约束条件下的优化结果中，优化模型的结果将更符合实际频谱需求。

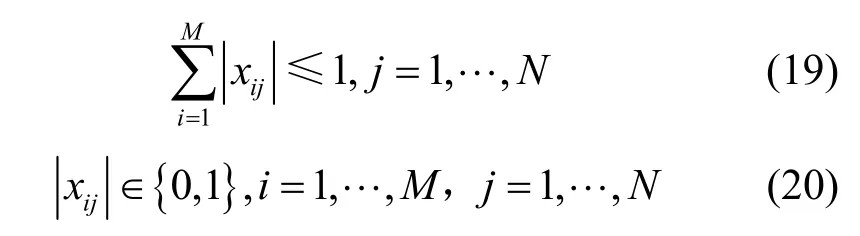
3.6 算法步骤及流程

在双目标WOA频谱共享算法中，需要优化变量xij的值，所有的xij可组合成M×N维向量，将其转换为一维向量记为

那么在双目标WOA频谱共享算法中，只需要将待优化变量[x11,...,x1N,x21,...,x2N,...,xM1,...,xMN]、式(16)和式(17)的优化目标加入算法进行优化即可。具体步骤如下。

Step1进行参数初始化，随机分配参数[x11,...,x1N,x21,...,x2N,...,xM1,...,xMN]，即在初始条件下，认知用户随机分配频谱资源。

Step2根据式(16)和式(17)计算初始参数下认知用户的优化目标和授权用户的优化目标。

Step3开始进入双目标WOA优化，结合第2节，通过WOA的鲸鱼行走觅食阶段、鲸鱼包围阶段和鲸鱼螺旋捕食阶段实现参数[x11,...,x1N,x21,...,x2N,...,xM1,...,xMN]的迭代更新，并同时计算对应的优化目标函数值。

Step4将每次迭代计算得到的优化目标函数值和当前迭代的最优目标函数值进行对比，并获得较优的目标函数值。

Step5重复上述步骤，直到完成所有的迭代计算，将最后迭代输出的参数[x11,...,x1N,x21,...,x2N,...,xM1,...,xMN]作为最后的优化结果，即频谱分配结果。

双目标WOA频谱共享算法流程如图3所示。

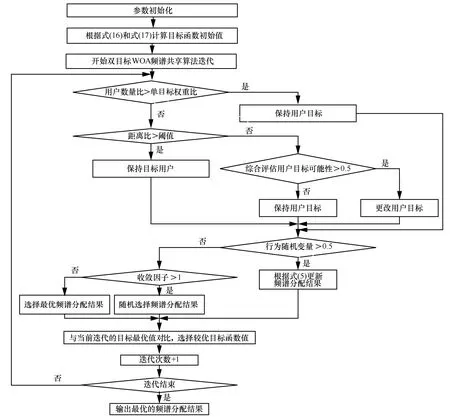
图3 双目标WOA频谱共享算法流程

4 性能测试与分析

仿真实验参数如表1所示。本文算法将与基于Bertrand博弈算法和基于Stackelberg博弈算法进行对比仿真，其中，基于Bertrand博弈算法无法反映实际的频谱需求，属于静态博弈；基于Stackelberg博弈算法可以反映实际的频谱需求，属于动态博弈。通过与这2种博弈进行对比，可讨论不同博弈对仿真性能的影响。

表1 仿真实验参数

价格纳什均衡点和频谱请求带宽纳什均衡点的仿真结果如图4和图5所示，这2个均衡点是与性能相关的分技术指标。由图4可知，2个授权用户的价格呈正向变动，这意味着当一个授权用户提高价格时，另一个授权用户也会提高价格，其反应函数曲线呈y=x对称形式。图4中，P1和P2表示授权用户1和授权用户2的归一化价格。由图5可知，2个认知用户的频谱请求带宽与授权用户价格呈反比，即授权用户价格越低，请求带宽越高。认知用户的请求带宽提高会降低授权用户的频谱价格，间接提高授权用户出租的频谱资源，从而提高认知用户和授权用户的收益，进一步提高系统效用，而系统效用的提升也意味着通信系统的吞吐率的提升。由图4和图5可知，基于Stackelberg博弈算法相对于基于Bertrand博弈算法，其频谱价格有一定程度的降低，而认知用户的频谱请求则较大幅度提升。而本文算法中，各授权用户在参考其他授权用户的价格后才给出价格，因此其最终的价格将低于基于Stackelberg博弈算法的博弈模型，而其对应的认知用户频谱请求则最大。

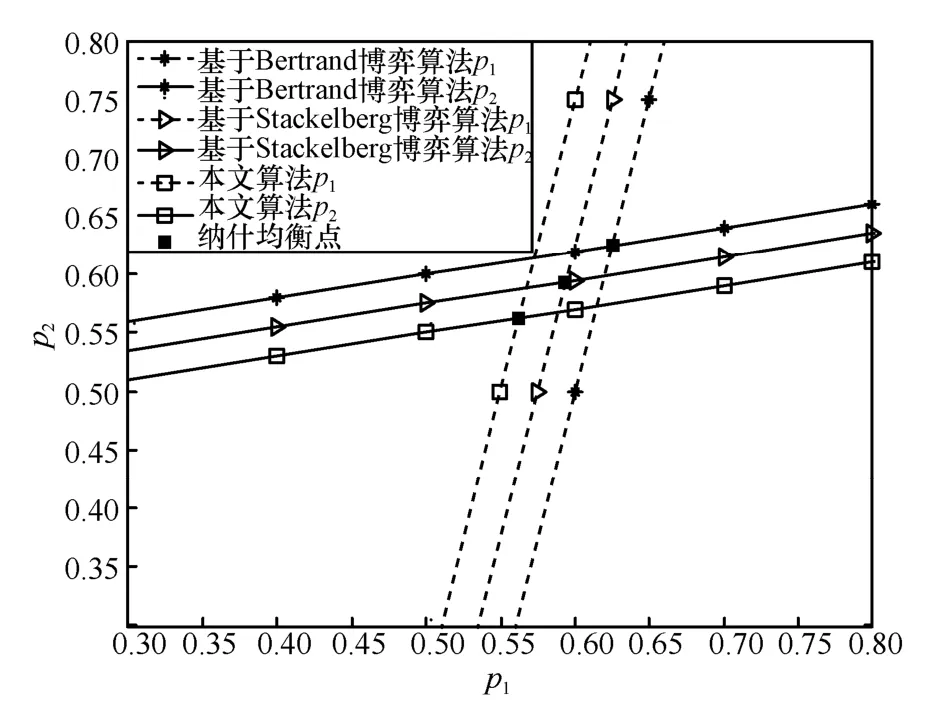
图4 授权用户的价格纳什均衡点

最佳授权价格随可出租的闲置频谱资源增加而变化的仿真结果如图6所示，最佳授权价格是与性能相关的分技术指标。由图6可知，随着可出租的闲置频谱资源的增加，为了让更多的认知用户购买频谱资源，其最优的授权价格逐渐减低。当闲置频谱资源增加到一定程度时，为保证授权用户的收益，其授权价格将趋于稳定。其中，基于Bertrand博弈算法考虑的情况较为理想化，认为博弈参与者最优价格最大，从而使认知用户收益降低。基于Stackelberg博弈算法相对于基于Bertrand博弈算法更符合实际情况，能够吸引更多的认知用户来购买频谱资源，因此得到的最优授权价格低于基于Bertrand博弈算法的价格。本文算法采用了基于Stackelberg博弈算法，各个授权用户在参考其他授权用户的价格后才给出价格，最终的价格将低于基于Stackelberg博弈算法，因此具有最低的授权价格。3种算法的最终价格分别为5.95（本文算法）、6.36（基于Stackelberg博弈算法）、7.03（基于Bertrand博弈算法）。本文算法的最终价格为基于Bertrand博弈算法价格的84.64%，为基于Stackelberg博弈算法价格的93.55%。

图6 授权频谱最佳授权价格变化

授权用户收益随着可出租的闲置频谱资源增加而变化的仿真结果如图7所示，授权用户收益是与性能相关的分技术指标。由图7可知，随着可出租闲置频谱资源的增加，授权用户的收益逐渐增加，这是由于当闲置频谱资源逐渐增加，其售价不断减低，从而吸引更多的认知用户购买频谱资源。当闲置频谱资源大于5的时候，随着认知用户的频谱需求逐渐得到满足，授权用户出售的频谱价格逐渐趋于稳定，系统的整体收益也逐渐平稳。同理，由于基于Bertrand博弈算法假设博弈参与者的条件是完全相同的，在实际的系统中的最优价格最大，导致参与购买频谱资源的认知用户较少，因此整体的收益最低。基于Stackelberg博弈算法的频谱价格小于基于Bertrand博弈算法，因此整体收益更高。本文算法采用了基于Stackelberg博弈，价格最低，参与购买的用户数量也最多，因此整体收益也最大。3种算法对应的授权用户的最终收益分别为455（本文算法）、364（基于Bertrand博弈算法）、418（基于Stackelberg博弈算法）。本文算法授权用户的收益相对于Bertrand博弈算法价格提升了25%，相对于基于Stackelberg博弈算法价格提升了8.85%。

认知用户收益随着可出租的闲置频谱资源增加而变化的仿真结果如图8所示，认知用户收益是与性能相关的分技术指标。由图8可知，随着可出租的闲置频谱资源的增加，认知用户的收益逐渐增加，由于频谱资源价格的不断降低，对于购买者认知用户来讲，其收益逐渐增加，当闲置资源数量大于20时，绝大多数认知用户的频谱需求得到了满足，授权用户出售的频谱价格也趋于稳定，因此其收益保持不变。由于基于Bertrand博弈算法假设博弈参与者的条件是完全相同的，因此该算法应用到实际的系统中，其最优价格最大，认知用户的收益自然也就最小。而基于Stackelberg博弈算法，其频谱价格小于基于Bertrand博弈算法，认知用户的收益较高。而本文算法的价格最低，认知用户的收益也最大。3种算法对应的认知用户的最终收益分别为2 789（本文算法）、2 563（基于Bertrand博弈算法）、2 307（基于Stackelberg博弈算法）。本文算法中认知用户的收益相对于基于Bertrand博弈算法价格提升了20.89%，相对于基于Stackelberg博弈算法价格提升了8.82%。

图7 授权用户收益

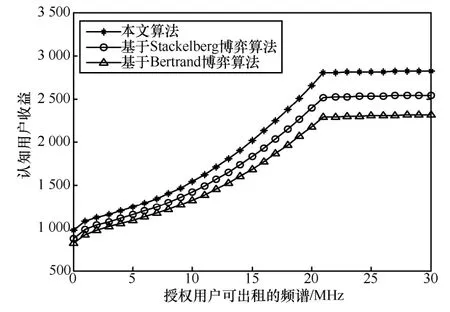
图8 认知用户收益

系统效用是系统的技术指标，系统效用随用户数量的变化情况如图9所示。由图9可见，随着用户数量的逐渐增加，不同博弈模型下的系统效用均逐渐增加。若都不考虑认知用户公平度，基于Bertrand博弈算法及基于Stackelberg博弈算法的系统效用均比本文算法低，这是由于仿生智能算法具有强并行计算能力，经过复杂的迭代优化获得了较优授权用户受益和认知用户受益，因此其系统效用将会更高。

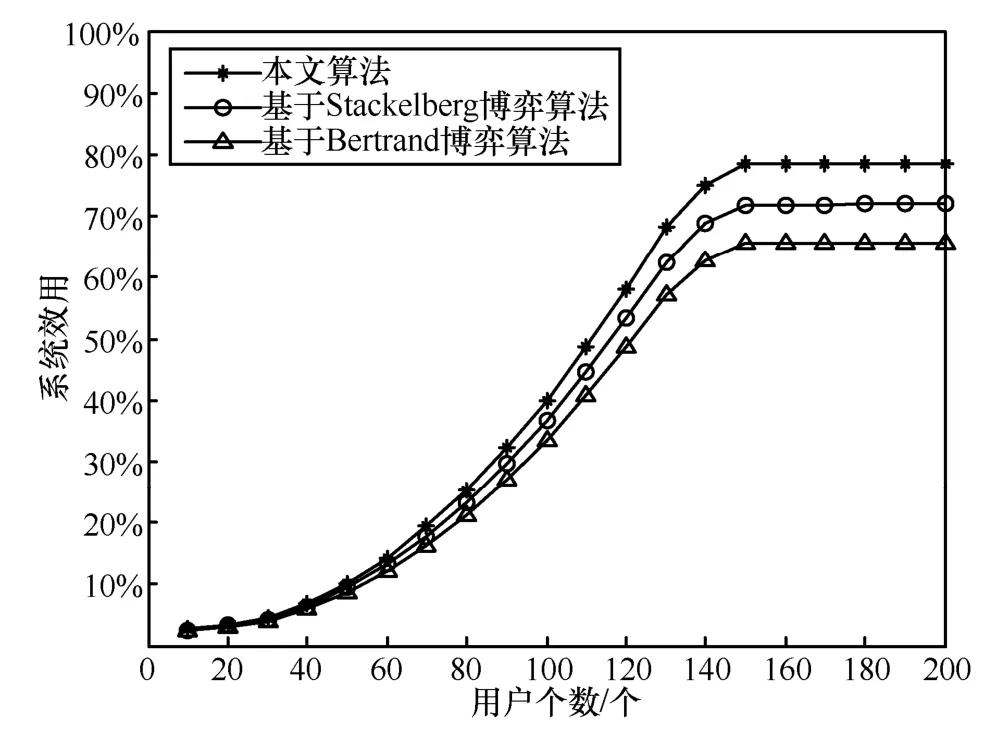
图9 系统效用

图10给出了不同公平加权系数δ3对算法性能的影响，分别设置δ3=0.9、δ3=0.5、δ3=0.1。公平度是通信性能的技术指标，它和通信网络的业务吞吐率是相互矛盾的，如果公平度越高，通信网络的业务吞吐率将会越低，如果公平度越低，通信网络的业务吞吐率将会越高。由图10可知，对比3种算法的系统效用，当公平度加权系数较小的时候，频谱资源分配受认知用户信道质量影响较小，本文算法可以获得更高的系统效用，而当公平度加权系数较大的时候，由于算法过于强调公平度，信道较差的认知用户也能获得较多频谱资源，反而影响了最终的系统效用。因此，在实际中，需要根据用户的实际需求来设置加权系数。

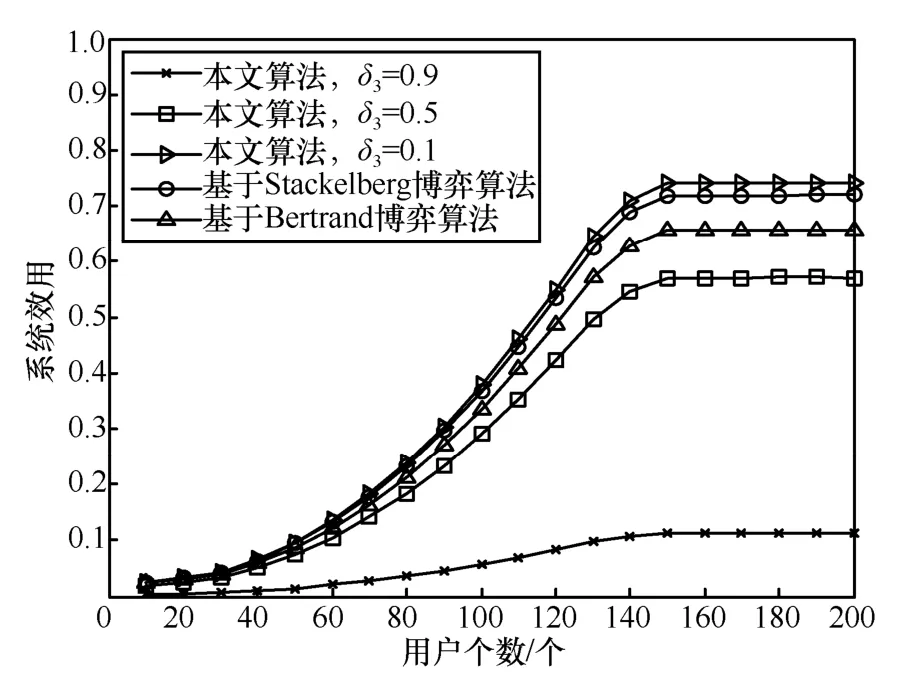
图10 不同公平加权系数δ3对系统效用的影响

图11给出了对200个用户使用3种对比算法其对应的公平度指标，此时由图11可知，由于本文算法在频谱分配过程中，考虑了频谱分配公平度指标，因此进行频谱分配时具有最高的公平度，平均达到了86.8%。而基于Stackelberg博弈算法虽然考虑了实际博弈过程的特点，但是由于没有涉及公平度的因素，其最终分配结果所计算得到的公平度只有71.3%。基于Bertrand博弈算法假设了各个博弈参与者完全相同的条件，因此在实际中，无法获得较好的频谱分配结果，其公平度只有59.2%。

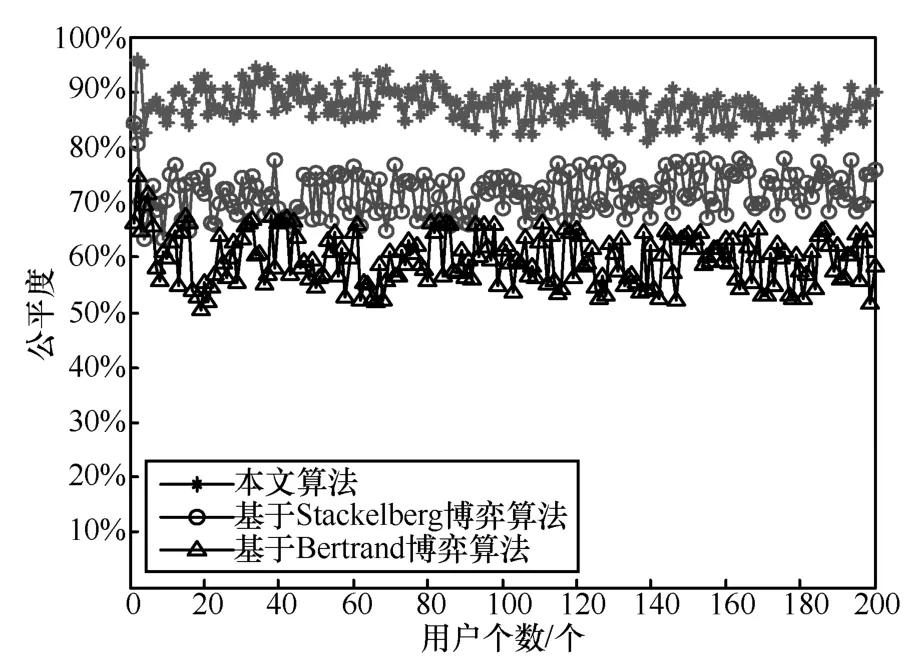
图11 系统公平度指标对比

图12给出了3种对比算法对应的仿真时间，其是与通信相关的分技术指标，对认知用户数量从10逐渐递增到200的仿真时间进行对比。由图12可知，本文算法的仿真时间最长，因为通过双目标WOA优化需要迭代，这会增加算法的复杂度。而基于Bertrand博弈算法的实现复杂度最小，因此其仿真时间最短。

图12 算法仿真时间对比

通过以上分析，在考虑公平度的情况下，本文算法的复杂度和仿真时间虽然不占优势，但其他性能优势明显，故本文算法在整体上有较为明显的性能优势。

5 结束语

通过分析WOA的特点及应用对象，提出了一种双目标WOA频谱共享算法，并给出了算法步骤和流程。本文基于Stackelberg博弈，引入强并行计算能力的双目标WOA，加入影响认知用户公平分配的函数，建立基于Stackelberg博弈的双目标WOA频谱共享算法。仿真结果符合预期目标，在算法复杂度、仿真时间和系统效用方面性能虽稍占劣势，但其他性能均取得较好结果，因此，所提方法在博弈论的频谱共享中有一定探索价值。