捻制系数不等式的建立及证明
2020-10-10沈志军佟玉飞赵宪海彭桂嘉魏晓旭
沈志军, 佟玉飞, 赵宪海, 彭桂嘉, 魏晓旭
(1.咸阳宝石钢管钢绳有限公司, 陕西 咸阳712000; 2.鞍钢钢绳有限责任公司, 辽宁 鞍山114000)
0 引言
用户根据工况和设备参数,可确定钢绳使用直径,然后将数据提供给钢绳生产商,以便生产商制造钢绳.然而钢绳是由数百根钢丝甚至上千根钢丝捻制而成,所以钢绳一般不采用一次捻制. 生产中,钢绳通用制造方法包括捻股和合绳等生产阶段. 制造过程会引入一个未知的股直径参数,然后才能用股合成钢绳. 这种由绳直径倒推股直径参数的比例系数一般称为捻制系数. 钢绳设计中,工程师特别关注捻制系数的取值,根据文[1-2]可知,捻制系数计算涉及一元四次方程求解,对于工程师而言,求解一元四次方程是困难的工作. 为计算捻制系数,文[3]求解了捻制系数的理论计算公式.
钢绳工作者指出如下问题:尽管文[3]已证明理论公式,但利用计算器等工具计算捻制系数并不容易,若能给出捻制系数下限也特别有意义. 因此,本文讨论了捻制系数不等式的建立过程,并给出了证明.
1 捻制系数精确解
为描述方便并兼顾钢绳工业的习惯,约定捻制系数为m,中心角为φ(φ是锐角),捻距倍数为K(K>π),股根数为N,π(圆周率)为常数,捻角为α.
文[1]中,参数关系如下

字符除m外,其他字符为已知常量,且各参数均为正值. m的理论计算式即[3]

2 捻制系数下限
实际中,如果将钢丝不经过捻制而直接放在一起,则有K→+∞,此时可给出m的下限[4],如下所述.
当K→+∞,则

3 建立捻制系数不等式
2011 年,在理论分析的基础上,笔者曾在《不等式研究通讯》中提出:
笔者称式(7)为捻制系数不等式.
4 证明捻制系数不等式
在北京师范大学物理学系白在桥教授的指导下,笔者证明了式(7).
4. 1 证明方法的形成
注意式(7)中的m(K,N)来自于式(1),因此

式(8)中,若f(m)=0,则
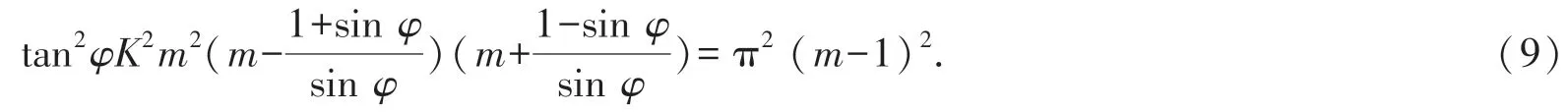
设式(9)等式左边的四次函数为L(m),再设右边的二次函数为R(m).将L(m)与R(m)画在一个坐标系,见图1.图中用φ=π/6、K=3.15 演示.
根据图1 可见: 1)函数L(m)的4 个根,依次为-(1-sinφ)/sinφ、0、0、(1+sinφ)/sinφ; 2)当0<m<(1+sinφ)/sinφ,L(m)<0. f(m)=0 有两实根m1、m2,两根数值:m1<(-1+sinφ)/sinφ,m2>(1+sinφ)/sinφ,可见含有m2的不等式就是捻制系数不等式.
据此需要分析的f(m)各阶导数函数性质,然后根据零点定理证明捻制系数不等式.
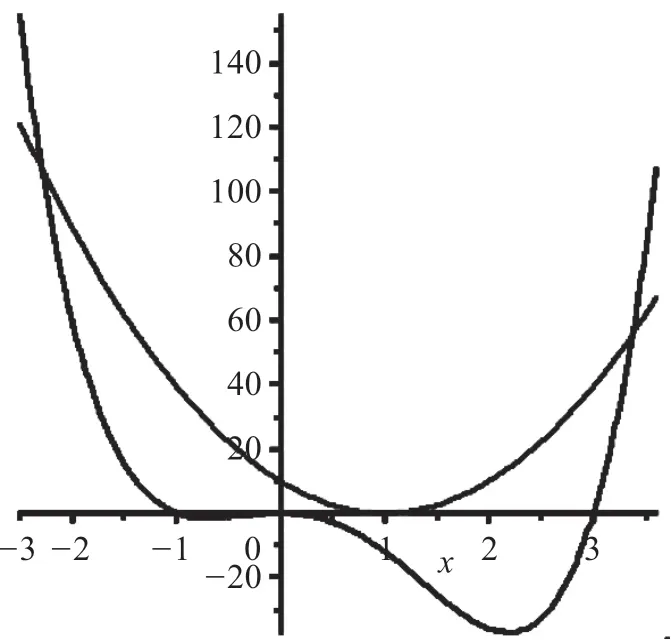
图1 二次函数R(m)与四次函数L(m)的仿真
4. 2 f(m)各阶导数的函数性质
为方便讨论,约定m∗=(1+sinφ)/sinφ,根据式(1)得[5]
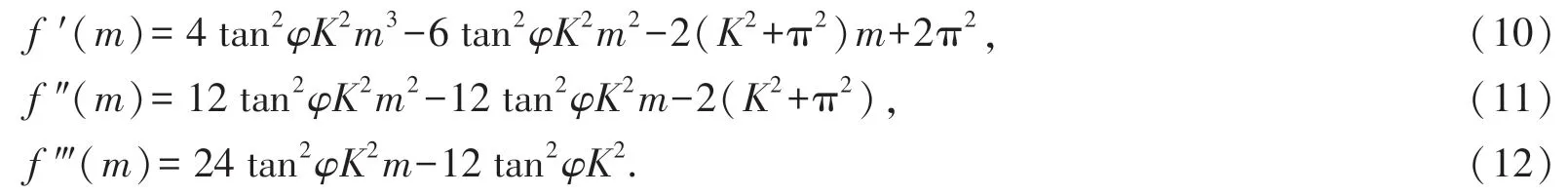
当m>m∗时,有f ‴(m)>0,则f ″(m)为增函数.因此,
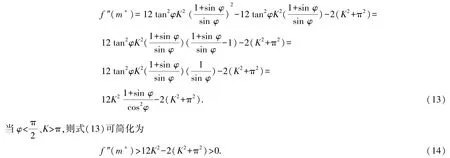
即m>m∗时,有f ″(m)>0.
改写式(10)中f ′(m∗),即

其中:g(m∗)=2K2m∗2-3K2m∗-cot2φ(K2+π2).
如果g(m∗)>0,则f ′(m∗)>0.实际上,

即f ′(m∗)>0.
因此,K>π 且m>m∗时,f(m)为增函数.另一方面,f(m)各阶导数均为多项式,根据高等数学可知连续.
综上所述,K>π 且m>m∗时,f ‴(m)>0,f ″(m)>0,f ′(m)>0;f ‴(m)、f ″(m)、f ′(m)以及f(m)为增函数且连续.将m∗代入可知f(m∗)<0,而f(+∞)>0.因此根据零点定理,存在m∈(m∗,+∞)使得f(m)=0,即式(7)成立.
5 推广捻制系数不等式
近期,在微分几何基础上,笔者建立钢丝绳参数关联因子n的概念[6].经过咸阳宝石公司多位工程师的努力[7-8],发现n和m存在函数关系.因此,笔者对于捻制系数不等式的证明有了新理解,此外推广了捻制系数不等式.
5.1 捻制系数下限的简单证明
在式(9)中,令K→+∞,可得

注意到m>0,可得

为了直观说明5.1 的含义,见图2.
图2 直接说明了本文建立的捻制系数不等式的含义.
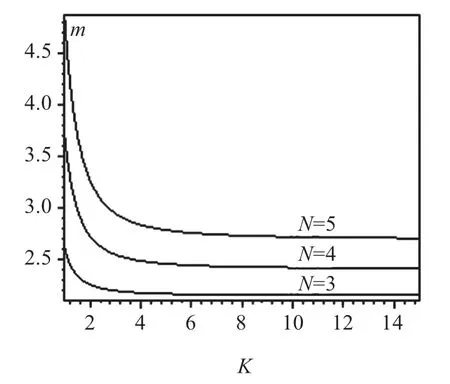
图2 N 与K 对m 的影响示意图
5.2 推广捻制系数不等式
钢丝绳参数关联因子含有很多对称性,受n启发,建立推广的捻制系数不等式.

其中:Δ 与式(2)相同.除m1外,其他字符为已知常量,且各参数均为正值,则

5.3 两类捻制系数不等式的统一证明
将式(9)变形为

在m∈R、K>π 下,

则

式(23)的正确性可用文[3]的数据检验.
必须指出:式(23)对于认识钢丝绳参数关联因子n有重要意义.式(23)反映出与n相关参数具有函数对称性.笔者曾和孙冠工程师猜测:除了实数表达式,n具有复数表达式.根据文[3],关于m的一元四次方程有2 个实根、2 个复数根,而n与m存在函数关系,即通过m可直接说明前述猜测正确.
6 讨论
工程不等式背景深刻且应用广泛,它值得理论工作者关注,文[9]给出了一些工程不等式的例子.工程中的不等式对于产品质量控制等方面有积极意义,解决工程中与不等式相关的问题,经常会涉及不同的数学分支,它是很好的应用数学方向.美国劳伦斯实验室的邵美悦老师曾对笔者说过,数学证明过程有助于理解工程结果的合理性.捻制系数不等式左边表示m的“实际值”,而右侧表示m的“理论值”.捻制系数不等式表明:理论的钢绳捻制系数m影响因素少于生产中的,即生产中不可以忽略捻制对钢绳的影响.通过捻制系数不等式的证明,笔者深刻体会了邵老师的观点.
致谢感谢陕西理工大学数学与计算机科学学院孙越老师的指导.
