多移动机器人分层优化调度算法研究

郑誉煌， 卜国富， 聂永怡

（1.广东第二师范学院 教务处， 广东 广州510303；2.广东第二师范学院 物理与信息工程系， 广东 广州510303）

0 引言

随着我国老龄化问题日益凸显，人口红利逐渐消失，生产方式逐步向智能化转变. 在电子商务和物流业空前发展的今天，仓库自动化是实现高效物流的关键. 在工业自动化系统中，移动机器人主要用于对工件或产品进行搬运、装卸等操作. 在生产过程中，工业物料不断处于运输、加工、组装、装卸、存储等状态. 物料流通不畅，会影响企业的生产效率，严重的会导致生产的暂停. 引入移动机器人，解决了当前劳动力不足的问题，高效和准确完成物料的运输和装卸任务. 实际生产场景中，往往需要多台移动机器人同时协助解决一项任务，机器人的调度系统需要优化每个移动机器人的行走路径，避免路径重复，提高移动机器人的运行效率. 当前仓储物流面临着产品批次和货物种类多样化的挑战，传统的移动机器人调度方法已经难以应对这些挑战. 当多个货物的提货单同时到达时，如何在减少移动机器人数量的条件下，尽快把这些货物提取并搬运到目标地点是关键问题［1］.当前的研究主要是采用容量约束的车辆路径优化模型问题（Capacitated Vehicle Routing Problem ，缩写CVRP）处理［2－3］，而且这些算法的移动机器人数量是一个常数，导致在实际应用中受到很大的限制.

为了解决这个问题，本文提出了多移动机器人的分层优化调度算法（Genetic Algorithm－MobileRobot－CVRP，缩写GA－M－CVRP），本算法分为两个层次，第一层是基于0－1 规划模型，分析了每个生产任务所需要的移动机器人数量； 第二层是基于CVRP 模型，获得每个移动机器人的最优运行路径. 每层算法的求解都基于遗传算法. 仿真实验结果表明：对于智能仓库中的多机器人调度和任务分配问题，GA－M－CVRP 算法优于现有的算法.

1 模型分析

1.1 仓库布局模型

不同的仓库有不同的布局形式，本文采用了文［2－3］的网格n×n式布局，如图1 所示.

假设圆形区域是移动机器人工作起点和提取货物后交付地点，在矩形区域中是移动机器人的货物提取点.当机器人被分配任务时，移动机器人从圆形区域出发，沿着规划路径按顺序到矩形区域提取货物，最后返回圆形区域，记圆形区域是配送中心.在移动机器人取货和返回的这工作过程，假设：1）某一空间内有N处货物提取点，每个提取点的货物已经打包成标准的包装箱，每个提取点的货物量可以用包装箱的个数描述，每个提取点的货物量不完全相同.移动机器人从搬运这些货物开始，直至把全部货物搬运到配送中心为止，称为一个工作任务.在一个工作任务内，每个提取点的货物不会增加.2）移动机器人每到货物提取点，必须把这个提取点的货物全部一次取走，不能分多次提取.3）不考虑包装箱与移动机器人车舱内其他包装箱的碰撞和滚动情形，设某一个货物提取点i的货物量是Si，车舱的最大容纳货物量是S0.4）在不同批次的工作任务中，每个提取点的货物量是不同的.5）多移动机器人之间没有发生碰撞和没有发生相互道路阻塞，不存在未能完成提货任务的移动机器人.6）移动机器人运行速度v、提取一个包装箱时间t1和卸货一个包装箱时间t2是恒定值.

设M个移动机器人把N处提取点的货物全部搬运，第j个移动机器人所走过的路径长度是Lj，则所需平均耗时是

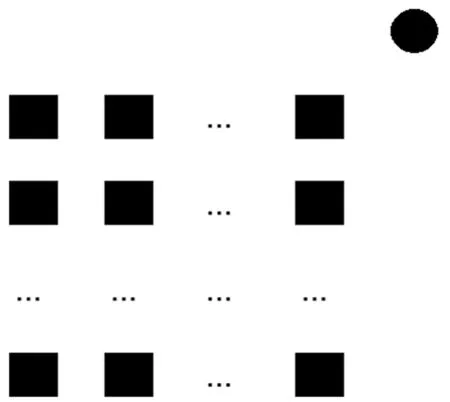
图1 参考布局

在同一批生产任务中，N、Si、t1、t2是不变的，移动机器人搬运所需耗时的可控变量是其所走过的移动机器人所走过的路径总长，这也是移动机器人在最短时间内完成一次工作任务的关键.

移动机器人货物搬运关键要解决两个问题，一是在给定一个生产任务后，完成此任务的移动机器人数量最小化； 二是对多移动机器人的路径进行优化，以达到最小运行距离.

1.2 所需移动机器人数量分析

移动机器人数量M的求解属于典型的一维装箱问题，可以建立如下0－1 规划模型：

目标：

约束：

式（2）为0－1 规划模型总求解目标，即每次工作任务所需要的移动机器人数量M最少； 式（3）表示每次搬运的提取点货物量总和不超过移动机器人的车舱容量； 式（4）限定了每个提取点的货物只能被搬运一次.式（5）中yi＝1 表示移动机器人第i次搬运时车舱有装入货物，反之表示移动机器人第i次搬运车舱是空载.式（6）中xij＝1 表示移动机器人第i次搬运时提取点j的货物装入车舱，反之表示提取点j的货物未装入车舱.

1.3 CVRP 模型

CVRP 可以描述为：以车辆总行驶距离最小为目的，在载运货物不超过其载重上限的前提下，合理调度车辆服务对象与运输路径［4］.

根据CVRP 的问题描述和上述模型假设，建立移动机器人搬运过程描述：一个移动机器人从配送中心空载出发搬运N个货物提取点，某一个货物提取点i的货物量是Si，移动机器人车舱的最大容纳货物量S0，而且满足移动机器人每到货物提取点，必须把这个提取点的货物全部一次取走，不能分多次提取； 每个货物提取点的坐标位置已知，则其相对距离可表示为di，j，每个货物提取点到配送中心的距离为d0，j； 由于车舱的限制，移动机器人不能一次搬运全部的货物，一旦车舱满载后，要回到配送中心卸货.移动机器人至少要搬运M次，设nk为第k次运送的货物数，集合Rk表示第k条路径，而元素rki中的i表示货物提取点rki在路径k中的顺序，配送中心为rk0＝0.从而建立如下的移动机器人搬运过程的多目标CVRP 数学模型.

目标：

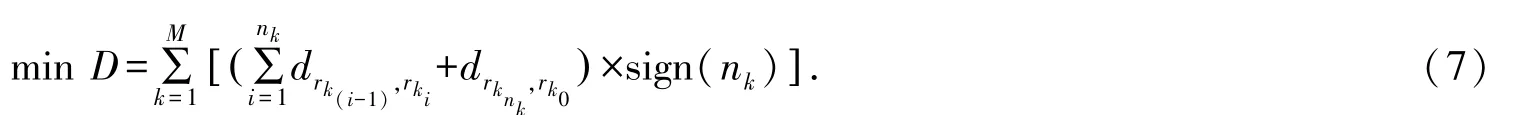
约束：

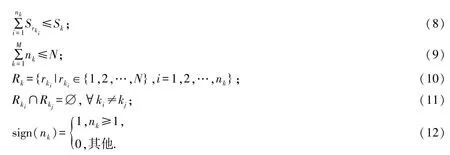
式（7）为CVRP 问题的总求解目标，即移动机器人总行走路径最短； 式（8）表示每条路径上的提取点货物量总和不超过移动机器人的车舱容量； 式（9）表示每个提取点货物都要被搬运到配送中心； 式（10）表示每条路径的提取点货物组成； 式（11）限制提取点货物只能由移动机器人搬运一次； 式（12）表示如果移动机器人第k次出发搬运提取点货物，则sign（nk）＝1，反之没有出发.

2 基于遗传算法的模型求解

2.1 遗传算法求解

根据上述分析，多移动机器人分层调度主要解决两个问题，一是最少移动机器人数，二是多移动机器人中的最短总行驶距离.这两个问题对应数学模型分别是0－1 规划模型和CVRP 模型. 0－1 规划模型和CVRP 模型都是NP 难题，高效的精确算法存在的可能性不大，主要研究是探索智能算法解决，最常见的智能算法包括模拟退火算法（Simulated Annealing）、禁忌搜索算法（Tabu Search）、遗传算法（Genetic Algorithm）、蚁群算法（Ant Colony） 和神经网络（Neutral Networks）方法等［4］.

随着问题规模的增大，组合优化问题的搜索空间也急剧增大，有时在计算上用枚举法很难求出最优解. 对这类复杂的问题，人们已经意识到应把主要精力放在寻求满意解上，而遗传算法是寻求这种满意解的最佳工具之一. 实践证明，遗传算法对于组合优化中的NP 问题非常有效. 本文解0－1规划模型和CVRP 模型所采用相同参数的遗传算法，其求解流程图［5］如图2 所示.

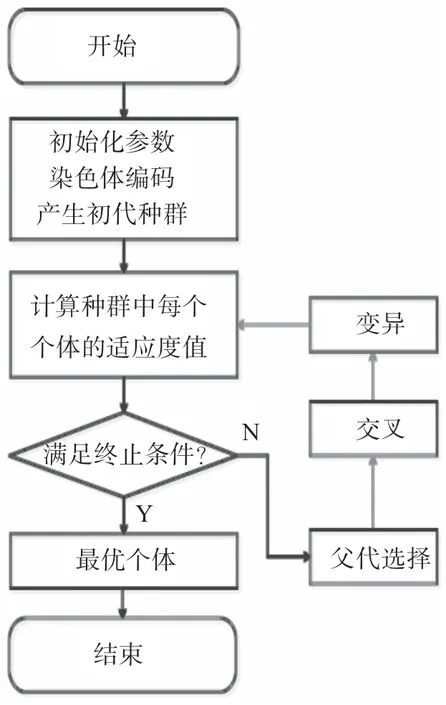
图2 遗传算法求解流程图

图3 分层优化调度算法

2.2 分层优化调度算法

本文所采用的分层优化调度算法（GA－M－CVRP）如图3所示，首先初始化遗传算法的参数和本次生产任务的货物提取点参数. 第一层基于遗传算法获得本次工作任务所需要的最少移动机器人数M0. 第二层在基于遗传算法获得本次工作任务的M0 个移动机器人的最优移动路径. 由于遗传算法的特点，或许会出现某个移动机器人所需要移动路径为0 的情况，即不需要M0 个移动机器人即可完成本次工作任务. 分层优化调度算法最后输出的是完成本次工作任务的实际需要移动机器人数和这些机器人的运行路径.

2.3 实验验证

由于0－1 规划模型和CVRP 模型都是NP 难题，遗传算法的每次求解不一定能获得最优解. 最优解即为保证每台移动机器人不超载的情况下，保证全体移动机器人的走过总路径最短. 在遗传算法参数是本算法中，设置最大迭代次数为Max ＝1 000，种群大小pop ＝40，交叉概率p＝0.4，变异概率q＝0.8，S0＝100，Si在（10，20）上均匀分布，即Si～U（10，20）.在每种布局的条件完成1 000 次随机的工作任务，获得结果如图4 所示. 实验结果可见，GA－M－CVRP 算法比文［3］提出的GA－CVRP 算法效果要好得多.随着布局规模的增加，两种算法的非最优率有所提高，但是GA－M－CVRP 在7×7 提取点布局以内的非最优率接近为0%，到了10×10 布局非最优率超过10%，而GA－CVRP 所得的非最优率几乎与布局规模的增大成正比. 采用GA－M－CVRP 算法后的平均减少行驶距离如表1 所示，在不同的布局下，本算法比GACVRP 获得的平均行驶距离有不同程度的减少，特别是随着提货点数量的增大，算法平均减少行驶距离越多，可见本算法是有效的.

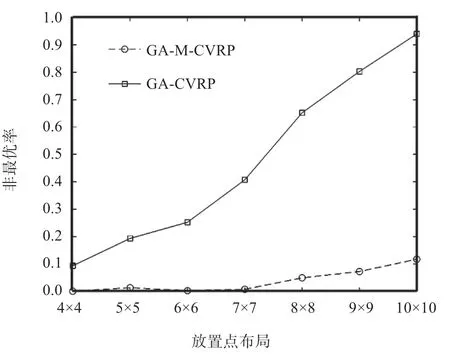
图4 不同放置点布局的非最优率对比

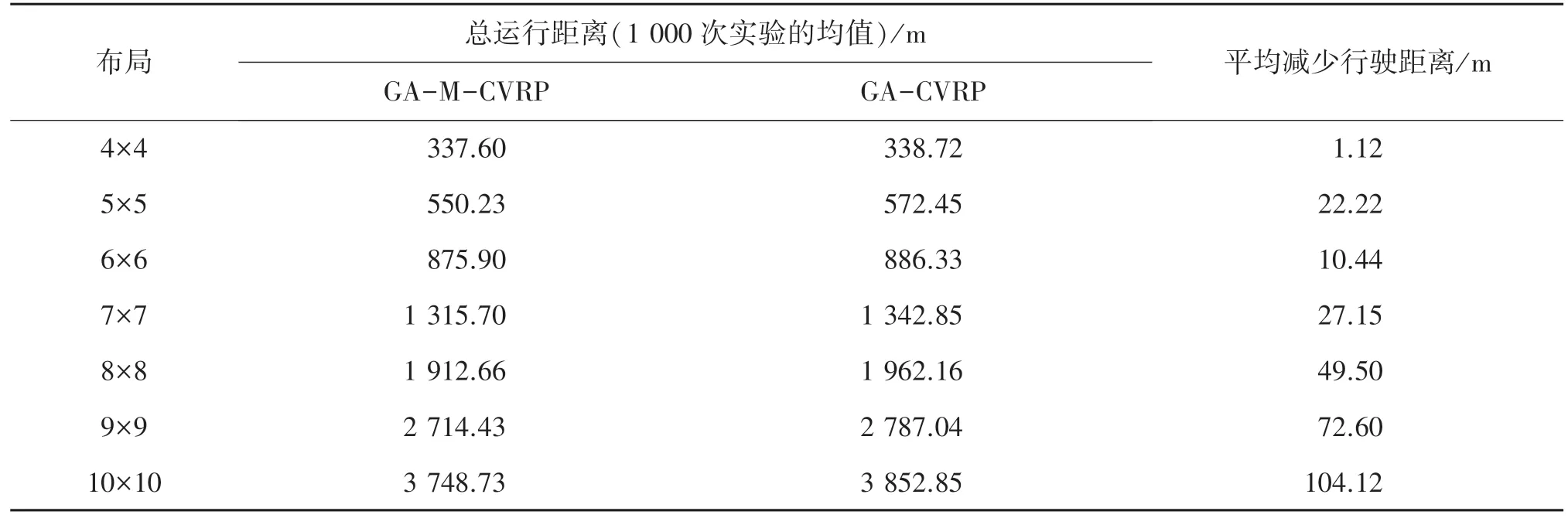
表1 不同布局的行驶距离分析

针对10×10 布局，修改遗传算法参数中的最大迭代次数分别为Max ＝1 000、1 500、2 000 和修改种群大小分别为pop ＝40、60、80 下，每个参数组合分别完成1 000 次随机的工作任务，所得的非最优率结果如图5所示. 可见在最大迭代次数Max ＝1 500 和种群大小pop ＝80 时，非最优率只有0.03 左右. 可以推断，对于小于10×10 的布局，非最优率会更小. 值得注意的是，10×10 布局在不同（Max， pop）组合下本算法获得的所需最少移动机器人数有一定差异，如图6 所示. 在Max ＝1 500 和pop ＝60 时，大部分情况下16 台移动机器人足够满足完成工作任务. 之所以出现15 台或17 台移动机器人的情况，是因为各个货物提取点在10 ～20 个标准箱子随机生成，最大需要机器人数20 台，最少10 台.

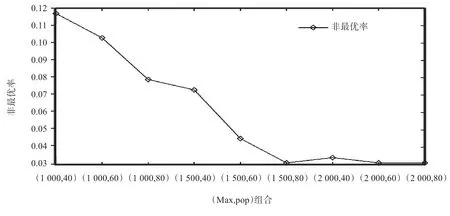
图5 10×10 布局时不同（Max， pop）组合下的非最优率

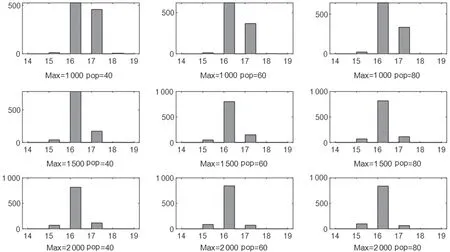
图6 10×10 布局在不同（Max，pop）组合下每1 000 次实验所获最少移动机器人数直方图

图7 是针对10×10 布局在1 000 次工作任务实验中，每次工作任务的实际提取货物量与本次所需要的移动机器人容量总和之比的直方图. 不同的遗传算法组合参数的实验结果如表2 所示，这个比值的均值在0.94左右，比值最小值超过0.85，最大超过0.98，说明本算法获得在遗传算法参数组合（1 500， 60）上基本达到较好的效果，保证了移动机器人负荷能在一定冗余的情况下满足所需要的提货量，但不至于出现仓位过度冗余的情况. 图8 显示了10×10 布局时不同（Max， pop）组合下的平均行驶距离分析，可见不同的组合会影响平均行驶距离的大小，一般Max 和pop 越大，平均行驶距离越小，但Max 和pop 的取值到了一定值后，平均行驶距离的减少量会不明显.

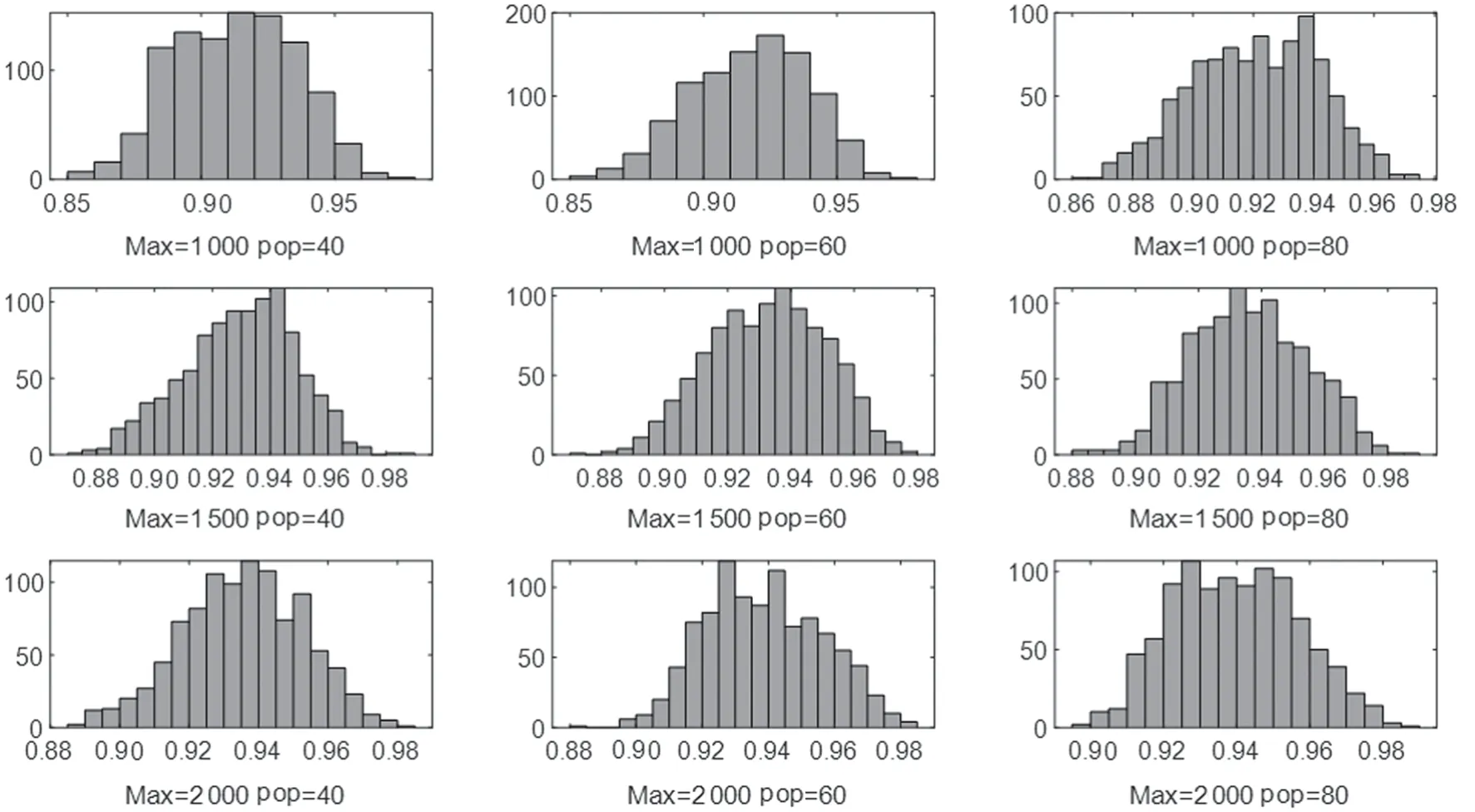
图7 实际负荷与移动机器人容量之比

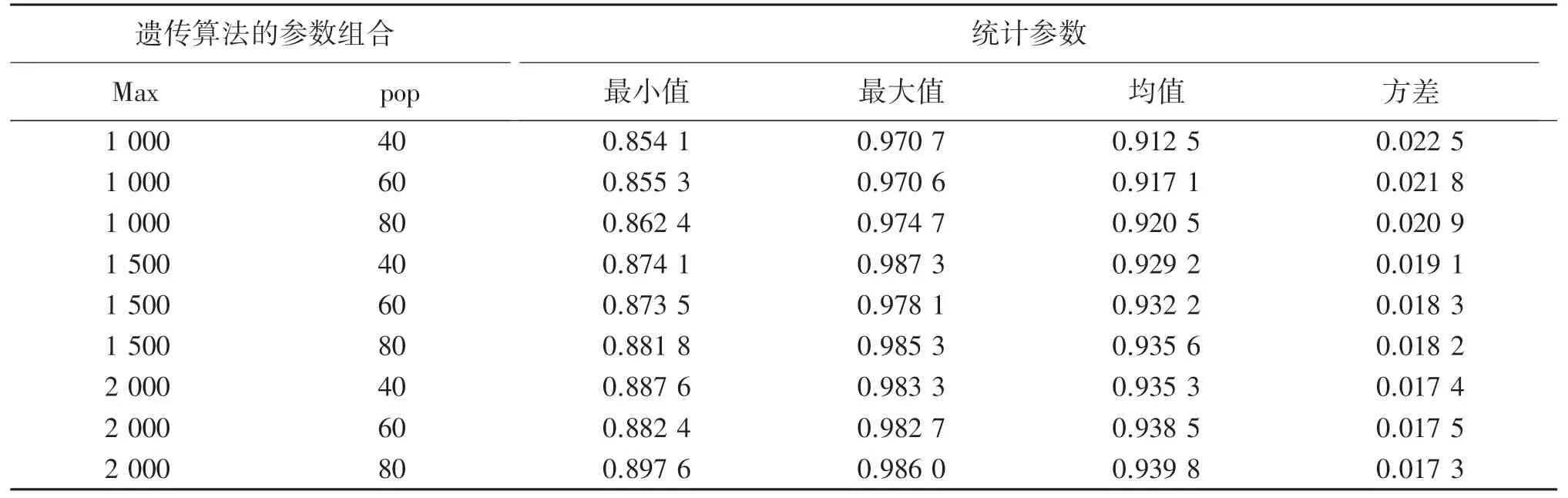
表2 实际负荷与移动机器人容量之比的实验结果表

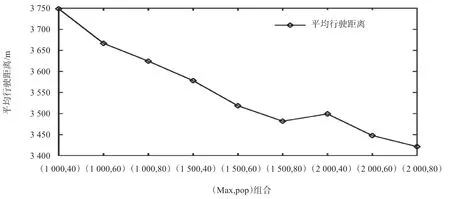
图8 10×10 布局时不同（Max，pop）组合下的平均行驶距离分析

3 结语

本文分析了多移动机器人在网格式布局仓库中搬运货物的特征，分析了多移动机器人在最短时间内完成一次搬运工作任务的关键问题，并提出了多移动机器人的分层优化调度算法GA－M－CVRP 解决这个问题. 本算法首先基于0－1 规划模型，分析了每个生产场景所需要的移动机器人数量，其次基于CVRP 模型获得每个移动机器人的最优运行路径，0－1 规划模型和CVRP 模型的求解均采用遗传算法以获得最优解. 仿真实验证明：本算法能较好实现多移动机器人在最快能完成各个提前点货物搬运，算法效果优于GA－CVRP 求解，并且保证每台移动机器人的仓位有一定合理的冗余，保证机器人不会过载运行，提高货物搬运的效率.本文尚未考虑移动机器人电池容量、载重、各个提取点货物在机器人搬运期间随机变化的情形，后续工作可以考虑将这些因素加入调度算法中进一步的分析.