不同止水方式对平面钢闸门静力特性影响分析

蔡许姣

(江苏省淮沭新河管理处， 江苏 淮安 223005)

平面钢闸门是水工建筑物常用的部件之一[1]。闸门与门槽埋件间止水位置布设不合理可能会导致止水的失效，止水的失效则会进一步引发闸门的漏水[2]、缝隙气穴、埋件气蚀破损等一系列问题[3]，严重时甚至会引发闸门结构的震动，影响闸门构件正常安全的服役[4]。为此，国内外诸多学者对于止水方式的设计作了相关研究。周和平等[5]研究了用于检修门强迫止水的弹压支承；熊威等[6]针对高水头闸门止水元件开展了非线性仿真分析；邓翼峰等[7]、钱军祥等[8]、时爱祥等[9]、薛小香等[10]基于实例工程的特点，针对不同的止水形式分别开展了设计及优化研究。而针对平面闸门止水系统布置的研究较少，目前闸门止水的布置形式主要分为前止水式与后止水式两种，具体布置方式一般均依据经验而定。基于上述背景，本文以某平面钢闸门为原型建模，分别采用前、后止水这两种止水方式进行对比计算，以期得到两种止水方式对闸门静力特性的影响，为同类水闸工程止水布置及结构的设计提供参考。

1 工程概况

以某水工平面钢闸门为研究对象，该闸门为潜孔式平面闸门，闸门尺寸4.50 m×3.60 m(宽×高)，板梁结构。面板由主横梁、水平次梁、纵梁以及边梁形成的梁格支承，梁格焊接在面板上。4根主横梁是截面为工字型的组合梁，从上至下编号依次为1～4号；3根纵梁为T形截面组合梁，从左至右编号依次为1～3号；边梁为II形截面组合梁，从左至右编号分别为1号和2号；6根小横梁为14号工字型钢，底梁为14号槽钢，从上至下编号依次为1～7号。闸门各构件的外形尺寸和厚度均按设计图纸取用。

2 模型建立

该平面钢闸门是一种较为复杂的空间薄壁结构体系，其主要由面板、主横梁、水平次梁、纵梁和滑轮构件组成。为准确反映闸门各构件的特性，得到精确度较高的计算结果，本次计算选用完整空间薄壁结构的仿真建模方式。上述各构件中，闸门的滑轮构件选用solid45实体单元，剩余结构均选用壳单元shell63。

2.1 计算模型及材料参数

为了便于对比计算结果，约束条件、材料参数、材料类型及长度等条件均保持一致，止水封条的位置分别设置在上、下游面，其位置前后相对应。整个模型结构离散成32 684节点，35 620个单元，闸门的结构和所受荷载均左右对称，整体的有限元模型如图1所示。闸门采用Q235钢材料。计算时材料弹性模量取E=2.06×105MPa，泊松比取ν=0.3，密度取ρ=7.8×103kg/m3。

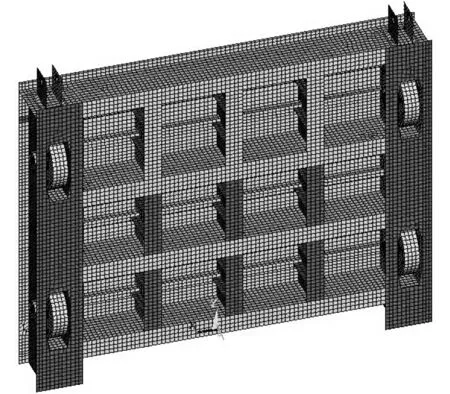
图1 结构网格模型

2.2 计算工况及边界约束条件

计算工况为设计工况：闸门作用水头25.00 m(底槛高程576.4 m)。为保持模型的几何性不变，假定模型底部面板的中间节点在闸门宽度方向位移为零，定义如下坐标系：以闸门主横梁轴向为x方向，以铅直向为y方向，以顺水流向为z方向。

2.3 荷载计算方法

由于此次计算是为了得到不同止水方式对闸门静力特性的影响，计算时仅考虑了闸门的自重与静水压力两个荷载。结构前止水的受水压力面为面板，后止水的受水压力面为顶梁腹板、面板、边梁腹板。两种不同的止水方式受水压力作用下的荷载面分别如图2和图3所示。

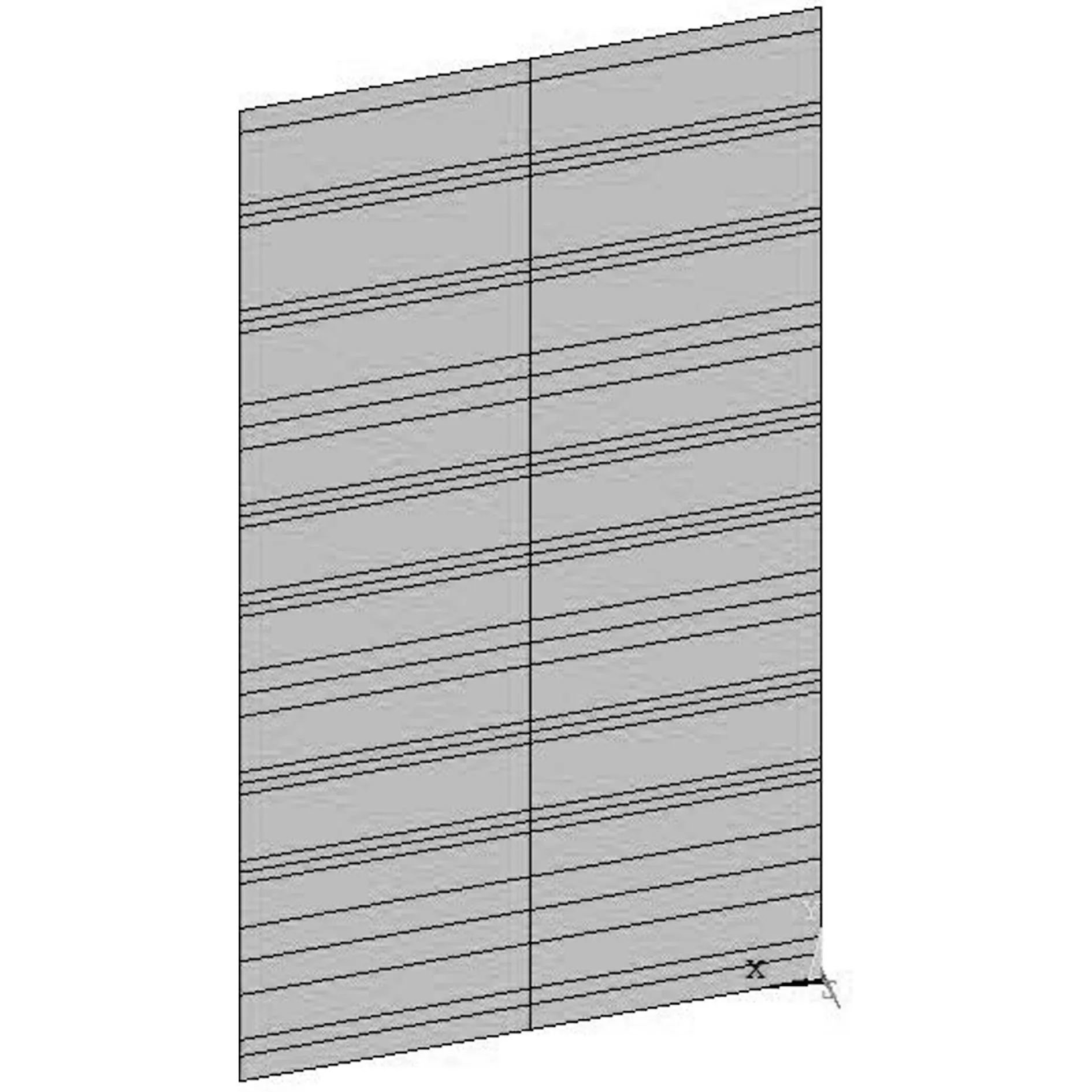
图2 前止水式闸门受水压力面

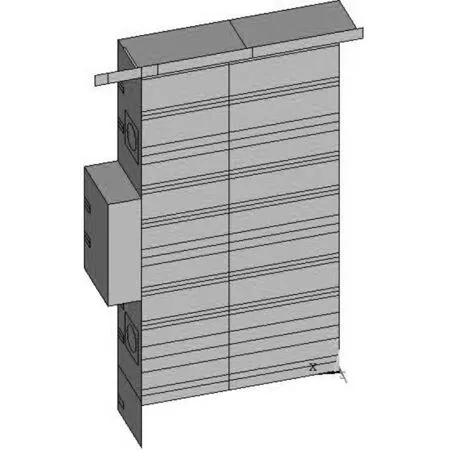
图3 后止水式闸门受水压力面

3 结果分析

3.1 应力分析

由于闸门模型左、右对称，因此只取其中左半部分(从水流方向视角观察)来取样分析。

3.1.1面板

图4为面板样点、区域位置示意图，平面钢闸门面板直接承受水压力。图5～6为面板在两种不同的止水方式时面板样点折算应力值对比图。

图4 样点、区域位置示意图

图5 面板1～4号样点折算应力

图6 面板5～8号样点折算应力

由应力计算结果可知：(1)后止水式平面钢闸门面板最大折算应力为90 MPa，最大应力出现在2号小横梁腹板、3号纵梁腹板与面板三者的交点上。前止水式平面钢闸门面板最大折算应力为105 MPa，比闸门采用后止水式时大了17%，最大应力出现在2号小横梁、2号纵梁内腹板和面板三者的交点上；(2)样点的应力值相差较小，最大差值为样点7，两者相差了3.72 MPa，其余样点应力差值均在1.78 MPa以下。表征此两种止水方式对于边梁之间的面板区域的应力影响不大；(3)面板应力分布在边梁所在区域处差别较大，即在图5中所表示的区域1到区域4。在前止水式时，区域1到区域4是不直接承受水压的，其中区域1与区域3存在应力较大的区域，该区域是面板与边梁内腹板的连接处区域，且小横梁也在此区域和边梁内腹板相交，导致面板在这两个区域处存在应力集中现象，折算应力最大值为105 MPa；而区域2中小横梁贯穿边梁腹板至面板两端，在该区域中未发生应力集中现象。在后止水式时，面板在z方向的两边均存在水压力的作用，在与前止水式面板应力集中区域相对应的地方未存在应力值很大的现象，从区域1到区域4，应力最大值为70 MPa；(4)两种止水方式对面板应力分布的影响主要在边梁所在区域，即区域1到区域4。综上所述，采用后止水式时，面板的应力分布要优于前止水式。

3.1.2主横梁

图7为1号主横梁1～5号取样点位置示意图，后止水式闸门1号主横梁直接承受水压力，2～4号主横梁则没有；前止水式闸门主横梁则未直接承受水压力的作用。图8为主横梁腹板最大折算应力值对比图，主横梁从上至下的编号依次为1～4号。

图7 1号主横梁1～5号取样点位置示意图

图8 1号主横梁腹板最大折算应力值对比

由应力计算结果可知：(1)前止水方式时，1号主横梁腹板最大折算应力值为76 MPa，后止水方式时，1号主横梁腹板最大折算应力为188 MPa，比闸门采用前止水方式时的最大折算应力大147%；(2)从1号主横梁样点折算应力图8可得，5个样点的折算应力值均相差较大，最大差值为105.81 MPa，最小差值为31.04 MPa。在对比图中，从样点4到样点5，两种止水方式下的应力值都下降较多，原因在于样点5靠近吊耳，而在吊耳处有加强板的存在，使得样点5处的应力值偏小；(3)平面钢闸门采用后止水方式时，主横梁腹板的折算应力值远大于采用前止水方式时的值。

3.1.3纵梁

结构的纵梁不直接承受水压力，其从左至右的编号依次为1～3号，由于在模型中1号纵梁和3号纵梁对称，所以只取3号纵梁作分析。图9为所取样点位置示意，腹板最大正应力值对比绘于图10中。

图9 纵梁1～8号所取样点位置示意图

图10 腹板最大正应力值对比

由应力计算结果可知：(1)后止水式时，平面钢闸门纵梁腹板最大轴向应力值为30 MPa，最大应力出现在1号、3号纵梁腹板与6号小横梁贯穿的开孔处区域。前止水式时，平面钢闸门纵梁腹板最大轴向应力值为32 MPa，比闸门采用后止水式时大了7%，最大应力出现在1号、3号纵梁腹板与4号主横梁上方区域；(2)样点1和5处的正应力值相差较大。2号纵梁腹板上，样点1在闸门采用后止水式时比采用前止水式时的值均大了2.05 MPa，在3号纵梁腹板上，比采用前止水式时的值大了7.67 MPa。其他样点在2号与3号纵梁腹板上差值较小，最大差值小于0.33 MPa，最小差值仅为0.09 MPa；(3)纵梁腹板靠近1号主横梁区域的正应力在闸门采用后止水式时要大于采用前止水式的值，这可能是由于采用后止水式时，闸门1号主横梁直接承受水压力，并且把一部分压力传递给纵梁，引起该区域的应力值大于采用前止水式的应力值；(4)两种止水方式对纵梁腹板正应力的影响主要在靠近1号主横梁区域，后止水方式时，该区域应力值大于采用前止水式时的值。

3.1.4边梁

后止水式结构边梁部分腹板直接承受水压力作用；而前止水式结构边梁未直接承受水压力作用。其从左至右的编号分别为1号和2号，由于两者为对称分布，因此只考虑其中的2号边梁。图11为区域位置示意图。

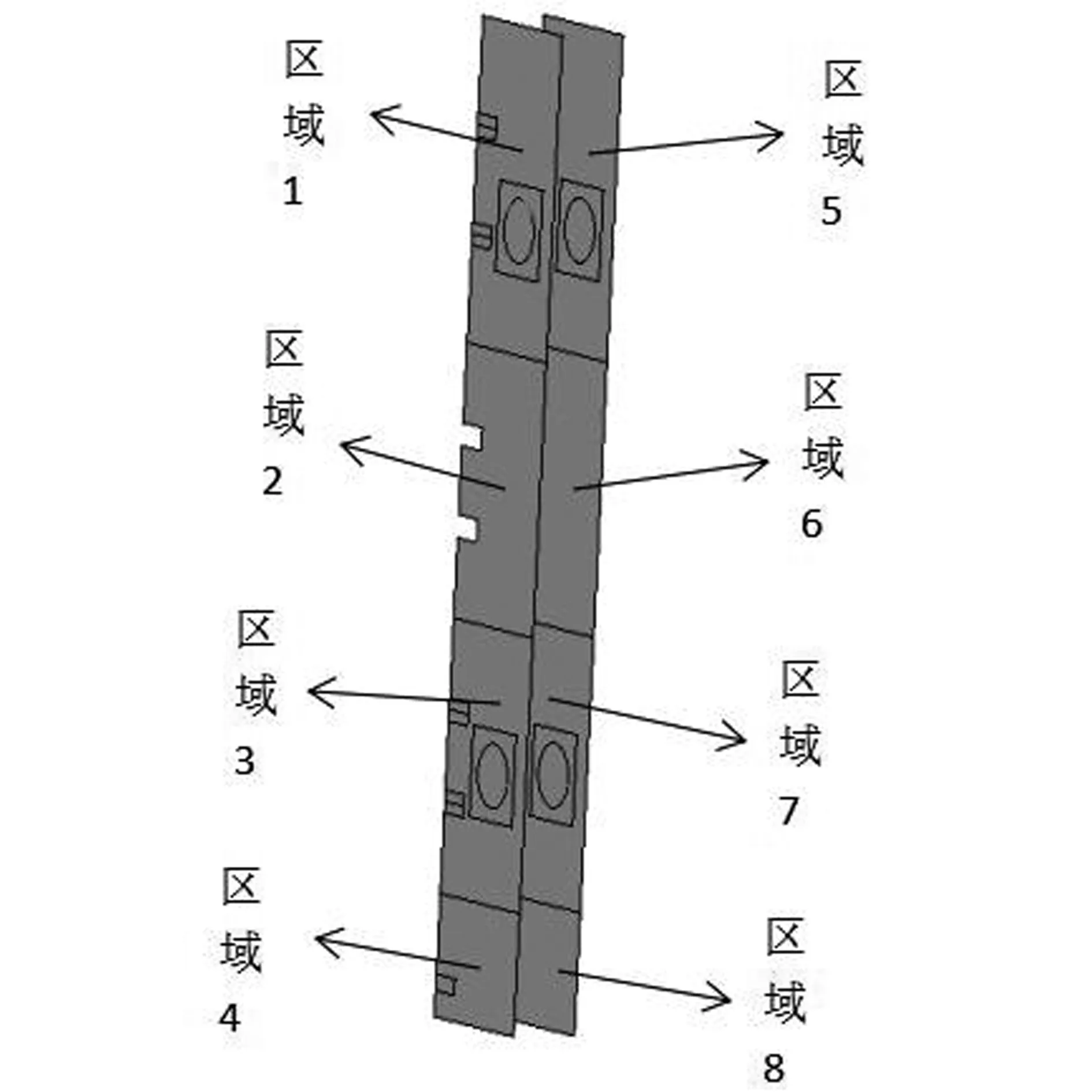
图11 区域位置示意图

由计算可得：(1)内腹板的应力分布差别主要在区域1、3、4三处区域。在后止水式时，区域1、3、4直接承受水压力，导致应力值大于区域2，应力最大值为126 MPa，区域1、3这两区域的中心处有应力比较小的区域，这是由于边梁腹板与轮轴交接处有加强板的存在。在前止水式时，区域1、3这两块区域在边梁腹板与轮轴交接处的周围区域存在应力值较大的小区域，可能由于定轮的存在，在闸门采用前止水式时，易产生应力集中现象，应力最大值为132 MPa，与后止水式时的差值为4%。在区域4中，由于闸门采用后止水式时，该区域直接承受水压力，导致应力大于前止水式。(2)外腹板的应力分布差别主要在区域6以及靠近区域6的部分小区域。这是由于在后止水式时区域6直接承受水压力，导致应力值较大，为108MPa；而在前止水式时，该区域则不承受水压力，也无应力集中现象，所以应力值的大小为13 MPa。(3)在后止水式时，边梁腹板部分区域直接承受水压力(即区域1、3、4、6)，导致该这几个区域应力值较大；闸门在前止水式时，区域1和区域3存在小区域内应力集中现象，导致最大应力值较大。

3.1.5小横梁

结构小横梁纵梁部分不直接承受水压力作用，小横梁(包括次梁和底梁)自上向下的编号依次为1～7号。

由应力计算结果可知：(1)后止水式时，平面钢闸门小横梁最大正应力值为128 MPa，最大应力出现在2号小横梁腹板与后翼缘连接处区域。前止水式时，平面钢闸门小横梁最大正应力值为126 MPa，比闸门采用后止水式时小了1%，最大应力出现在2号小横梁腹板与后翼缘连接处区域；(2)两条折线基本重合，相差最大处在4号小横梁，差值为4.7 MPa；(3)表征平面钢闸门止水方式采用两种不同的止水方式时，对小横梁的应力影响均较小。

3.2 位移分析

由计算结果可知：(1)后止水式时，平面钢闸门主横梁最大挠度变形量为2.63 mm，最大变形出现在主横梁腹板介于3号纵梁与2号边梁内腹板之间区域。前止水式时，平面钢闸门主横梁最大挠度变形量为3.15 mm，比后止水式时主横梁最大挠度变形量大了19.8%，最大变形出现在主横梁跨中区域；(2)前止水式时，1～4号主横梁的挠度变形量逐渐增大。后止水式时，1号主横梁的最大挠度变形量大于其他主横梁，且大于前止水式时1号主横梁的最大挠度变形量，两者差值为0.51 mm，这是由于该止水方式下，1号主横梁直接承受水压力，导致挠度变形量变大。后止水式时，2～4号主横梁的最大挠度变形量亦逐步增大，但最大挠度变形量均小于前止水式时相应主横梁，且差值均在1.22 mm以上；(3)在后止水方式下，闸门1号主横梁的最大挠度变形量大于前止水式时，2～4号主横梁的挠度变形情况则相反。总体而言，闸门在采用后止水方式时，主横梁的挠度变形情况优于采用前止水式时。

4 结 论

(1)由计算可知，两种止水方式下闸门各构件应力均满足强度要求，但局部位置易出现应力集中现象，针对这些薄弱区域，建议采取补强加固措施。

(2)后止水平面钢闸门面板和2～4号主横梁的应力分布优于前止水式，且最大应力值小于前止水式；两种止水方式对于主横梁的应力分布影响均较大；后止水方式对边梁的主要影响在于腹板直接承受水压力区域；边梁和1号主横梁的应力分布情况表明前止水式优于后止水式；两种止水方式的应力计算结果对小横梁影响均可以忽略。

(3)后止水平面钢闸门2～4号主横梁的挠度变形小于前止水式，由于后止水式闸门1号主横梁直接承受水压力的作用，导致1号主横梁挠度变形大于前止水式。经过整体综合分析，后止水平面钢闸门抗变形能力更强。