深海管道轴向定向移动消减方案研究

刘 润, 郝心童, 李成凤, 彭碧瑶

(天津大学 水利工程仿真与安全国家重点实验室, 天津 300072)

铺设于海床表面的深海管道, 在启闭操作和管内温压联合作用下, 极易发生轴向移动(pipeline walking)。海管轴向移动本身不会导致管道的破坏, 但由此造成的连接结构应力超标、钢悬链线立管(steel catenary riser, SCR)丧失预应力及侧向屈曲管段载荷增加是导致海底管道失效的重要原因。Bruton 等[1]指出, 现已在很多管道中观察到轴向移动现象, 其中有一起案例, 由于海管的轴向移动, 导致端部连接处断裂, 进而使海管系统发生故障。由此可见, 采用必要的工程措施消减海底管道的轴向移动量至关重要。

关于海底管道轴向移动现象的研究最早见于2000 年。Tornes 等[2]首先提出了由于瞬态热梯度作用导致的轴向“棘轮”效应, 并且根据管道的膨胀行为, 将管道进行了“长短”分类。此后很多学者针对海管的轴向移动现象进行了相关研究, 早期海底管道轴向移动的研究主要集中在诱发因素方面。2003 年, Carr 等[3]正式将海管的轴向整体移动命名为“walking”(本文翻译为轴向移动), 并分析了在瞬态热梯度作用与SCR 张力作用下管道发生轴向移动的机理; 2008 年, Carr 等[4]对walking 现象的诱发因素(海床斜坡, SCR 张力, 瞬态热梯度)进行了全面的描述与分析, 建立了各诱发因素下管道轴向移动的解析解; 2017 年, 彭碧瑶等[5]阐述了高温高压海底管道发生轴向移动的运动机理, 建立了单因素与多因素诱发管道轴向定向移动的数值模拟方法, 运用多元非线性回归分析了多因素诱发管道的轴向移动规律。此外, 在管道整体屈曲与轴向移动的耦合[6]以及管土相互作用模型对轴向移动的影响[7]等方面也不断有新的研究成果。

但对消减海底管道轴向定向移动方法的研究相对较少。2003 年Carr 等[3]提出对管道进行锚固可以抑制管道的轴向移动量, 但提出的最大锚固力理论计算方法与实测值相差较大, 因此后续研究主要采用有限元模拟。Carneiro 等[8]提出了一种简化的一维模型, 用来研究管道轴向移动现象, 结果显示一维模型计算得到的轴向移动量与复杂的三维模型相差在10%以内, 但锚固力结果与三维模型相差较大。为了探究不同模型锚固力结果差异的来源, Castelo 等[9]在Carneiro 等人的研究基础上, 针对同一工况建立了二维模型, 研究表明数据结果的差异源于模型的不同, 与采用的有限元软件无关, 2D 模型结果与1D模型非常相近, 与3D 模型相差较大, 同时Castelo 等指出, 最常用消减管道轴向移动的方法是在管道终端(pipeline end termination, PLET)使用锚链锚固, 或是将PLET 滑动基础与吸力桩刚性连接。其他关于消减海底管道轴向移动的措施多见于具体的工程项目,例如Demel 等[10]以西非海岸一个海底管道工程为例,提出采用海底混合基础的双锚固系统限制管道轴向移动, 并介绍了此锚固系统的设计、制造和安装过程。Carneiro 等[11]以Brazilian 海底管道工程中两个6 km 长的管道为例, 提出采用双枕木防止管道屈曲破坏, 采用端部锚链锚固限制管道轴向移动。综上所述, 对消减海底管道轴向移动措施的研究很少, 尚无锚固力的准确计算方法, 针对具体工程项目的研究并没有揭示规律, 因此不具普适性。

为解决不埋深海管道在温压荷载循环作用下,轴向移动量不断累积的问题, 本文针对Castelo 等[9]提出的消减管道轴向移动的两种方法开展有限元模拟分析, 并对锚链锚固的位置与形式进行优化, 针对一端为SCR, 一端为PLET 的典型短管模型, 提出采用中部单向锚链锚固结合端部滑动基础的措施是消减管道产生移动的最有效方法。

1 短管轴向移动诱因的敏感性分析

管道中有效轴力最大的点称为虚拟锚固点。升温时, 虚拟锚固点为管道膨胀的中心点, 即管道由虚拟锚固点向两端膨胀; 降温时, 虚拟锚固点为管道收缩的中心点, 即管道由两端向虚拟锚固点收缩。以往研究显示[4], 高温高压海底管道在受到SCR 张力、海床倾角及内部瞬态热梯度作用时, 可能会发生轴向移动。其主要机理为, 在以上3 种因素作用下, 升温时管道的膨胀中心点与降温时管道的收缩中心点不一致, 导致管道在冷却收缩后无法回到最初的位置, 因此产生轴向移动。管道轴向移动的产生依赖于管道的启闭循环, 若频繁启闭管道, 每一启闭循环产生的轴向移动将会累积, 最终管道会朝向受拉一端, 沿斜坡向下一端及升温滞后一端产生持续的严重的管道整体移动。

为比较SCR 张力、海床倾角及内部瞬态热梯度作用对海管轴向移动量的影响, 开展了管道轴向移动诱因的敏感性分析。升温过程中, 流过管道的热流造成的管道温度在时间和空间上分布的不均匀性称为管道内部瞬态热梯度。实际工程中, 管道开启时热流由热端向冷端移动并逐渐加热管道, 管道热端总是先被加热至设计温度, 因此管道内部一定存在瞬态热梯度作用。故在敏感性分析时, 主要针对瞬态热梯度与海床倾角顺向耦合, 瞬态热梯度与SCR 张力顺向耦合两种工况, 具体如图1 所示。

图1 敏感性分析模型Fig. 1 Sensitivity analysis model

图1 两种工况瞬态热梯度方向相同, 将管道坐标x=0 m 处设为管道热流入口, 即管道热端, 将管道坐标x=2 000 m 处设为管道冷端。工况a 中海床整体倾角假设为3°, 管道两端皆为PLET 端; 工况b 管道一端为PLET 端, 一端为SCR 端, 在风暴条件下,SCR 底部张力可达1 600 kN, 不考虑风暴条件, 管道正常启动下产生的SCR 张力一般为200 kN[12]。

应用ABAQUS 软件, 采用通过与经典解析解结果对比验证合理的静力算法[5], 建立了管道轴向定向移动数值模型。管道平直无弯曲, 全长2.0 km, 管道外径为0.273 1 m, 管道壁厚为0.014 4 m, 单位管重为689.07 N/m, 膨胀系数取1.1×10–5℃–1, 弹性模量为2.06×1011Pa, 泊松比取0.3, 建模时管道采用梁单元,单元类型为PIPE31; 土体全长2.1 km, 弹性模量为2.0×107Pa, 内摩擦角为18°, 土体密度为1 556.6 kg/m3,粘聚力为1 800 Pa, 泊松比取为0.3, 建模时土体采用实体单元, 单元类型为C3D8R。管土间接触选取罚接触和法向硬接触, 摩擦系数取为0.5。

SCR 张力以管道终端集中力的方式施加, 取SCR 底部张力为FSCR=200 kN。PLET 端采用非线性弹簧模拟, 力-位移关系曲线见图2。

图2 中以管道向冷端即x轴正向移动时，轴向移动量u为正；管道有效轴力P以拉为正。

管道开启时, 管道沿程逐渐升温, 将管道内部瞬态热梯度作用简化为线性曲线, 图3 为简化的升温曲线。

如图3 所示, 瞬态热梯度为20℃/km, 将此升温曲线写入inp 文件。假定海底环境温度为20℃, 管道开启时, 为保证油气的正常输送, 需将管道逐渐加热至150℃; 管道关闭后, 在周围海水的冷却作用下管道均匀降温至环境温度20℃, 将此开启关闭的过程视为一个循环, 用n表示。

图4 为图1 中工况a 的P-x图, A 表示降温过程的虚拟锚固点, B 表示升温过程的虚拟锚固点; 图5为两种工况管道热端轴向移动量u与循环次数n的关系曲线。

图2 PLET 力-位移曲线Fig. 2 PLET force-displacement response

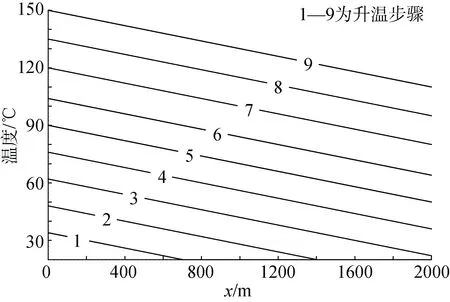
图3 升温曲线Fig. 3 Heating curve

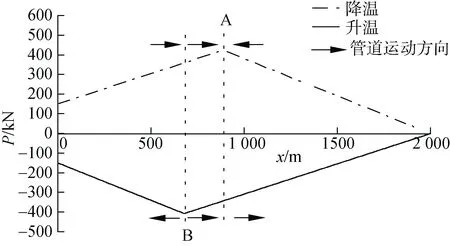
图4 工况a 管道有效轴力分布Fig. 4 Effective axial force profile of case a

图5 不同模型管道热端轴向移动量-循环曲线Fig. 5 Hot end walking vs. cycle of different models

由图4 可得, 降温过程的虚拟锚固点A 和升温过程的虚拟锚固点B 不重合, 锚固点两侧管道运动方向如图中箭头所示, 由于AB 段升温降温过程管道运动方向均指向沿斜坡向下一端, 因此管道向下坡发生整体轴向移动。由图5 所示, 管道在瞬态热梯度与SCR 张力顺向耦合情况产生的轴向移动量远大于瞬态热梯度与海床倾角顺向耦合情况。为进一步揭示SCR 张力相比其他两种因素对轴向移动的影响规律, 采用图6 所示的三因素综合作用模型, 并分别取SCR 张力为0, 100, 200 kN 进行计算。

图6 SCR 张力敏感性分析模型图Fig. 6 Model for SCR tension sensitivity analysis

仍将海床倾角取为3°, 瞬态热梯度取为20℃/km,且将管道坐标x=0 m 处设为管道热端。海床倾角使管道产生朝向热端的轴向移动, SCR 张力和瞬态热梯度使管道产生朝向冷端的轴向移动。图7 为FSCR=200 kN 时, 管道的P-x图。

由图7 所示, 由于AB 段升温降温过程管道运动方向均指向SCR 作用端, 因此管道向SCR 作用端发生整体轴向移动。降温时, 最大的有效轴力为516 kN;升温时, 最大的有效轴力为–301 kN。图8 为管道热端的u-n图。

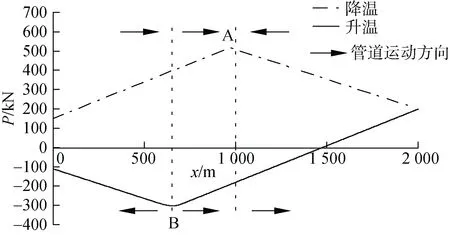
图7 FSCR=200 kN 下管道有效轴力分布Fig. 7 Effective axial force profile when FSCR = 200 kN

图8 不同SCR 张力下管道热端轴向移动量-循环曲线Fig. 8 Hot end walking vs. cycle under different SCR tensions

由图8 可知, 当FSCR=0 时, 管道会向热端移动,这是由海床倾角作用产生的, 其每循环轴向移动增量Δu=–0.238 m。当FSCR=100 kN 时, 管道会向冷端移动, 这是由于SCR 张力和瞬态热梯度的联合作用大于海床倾角的作用, 每循环轴向移动增量Δu=+0.113 m。当FSCR=200 kN 时, 每循环轴向移动增量Δu=+0.477 m, 10 个温度循环管道产生的整体轴向移动增量达Δu=+4.77 m, 最大轴向移动量u达到+5.98 m, 且轴向移动量u会随着n不断累积, 产生了工程中难以控制的累积轴向移动量, 对海底管道系统安全造成了巨大的威胁。

综上所述, SCR 张力对管道轴向移动的影响显著。因此以下针对如图6 所示模型(其中FSCR=200 kN)研究管道轴向移动的最佳消减措施。

2 最佳锚固方式的确定

2.1 锚固方案

1) 常见锚链系统组成

减少管道轴向移动的原理大致分为增加轴向摩擦力及施加外力两种[13]。工程上常采用的方法有使用混凝土配重层, 开沟/埋放, 局部抛石/沉排等, 但是这些方法在深海中都存在局限性。工程经验表明, 轴向锚固是一种消除深海管道轴向移动的常用方法, 具有很高的成功率和稳定性。图9 为管道中部锚固示意图。

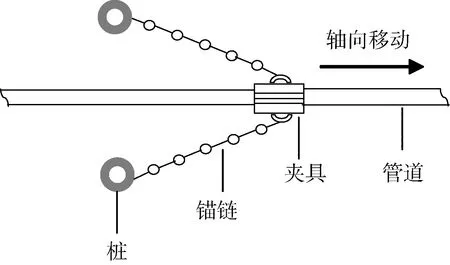
图9 管道中部锚固示意图Fig. 9 Anchor at the pipeline midpoint

工程中常采用锚链连接管道与锚桩。升温时, 允许管道自由膨胀通过锚桩; 冷却收缩时, 管道向背离锚桩的方向移动, 当管道回到初始安装位置仍继续朝背离锚桩的方向运动时, 锚链会产生拉力以消减轴向移动量。

2) 锚固计算方案

实际工程中可在管道沿程任何位置进行锚固,为了得到最有效的锚固方案, 可对锚的位置进行优化。本文提出六种锚固方案, 如表1 所示。其中单向锚仅限制管道发生朝向SCR 端的运动; 双向锚则限制管道朝向PLET 端和SCR 端的运动。

2.2 不同锚固方案计算结果

6 种锚固方案下分别计算了u与n的关系, 计算结果如图10 所示。

图10 6 种锚固方案管道轴向移动量-循环曲线Fig. 10 Walking vs. cycle for six anchor cases

由图10 可得, 相比于图8 不对管道进行锚固的工况, 6 种锚固方案每循环管道的轴向移动增量Δu均为0, 即6 种锚固方案均有效限制了管道轴向整体移动趋势, 使管道轴向移动量不会随着循环而不断累积。冷端移动量由大至小分别为方案2, 方案1, 方案5、6, 方案3, 方案4; 热端移动量由大至小分别为方案4, 方案3, 方案5、6, 方案1, 方案2, 即热端移动量与冷端移动量呈相反趋势, 其中方案5 及方案6 的热端与冷端u-n图相同。方案4 冷端移动量为0, 这是由于锚固在SCR 处的双向锚将管道锚固点的位移完全限制, 但方案4 热端移动量最大, 这是由于锚固点距离冷端较远, 不能有效控制冷端移动量; 同理, 方案2 热端移动量为0, 但冷端移动量最大。而方案5 及方案6 两端移动量均较小, 这是由于锚固点在中部时, 对两端的约束力较为均衡。虽然六种方案都有效控制了管道的轴向移动, 但每种方案中的管道有效轴力差异很大。

图11 为方案1 及方案2 的管道有效轴力分布图。图12 为方案1 管道降温过程中的有效轴力变化图。

图11 方案1 及方案2 有效轴力分布Fig. 11 Effective axial force profile of cases 1 and 2

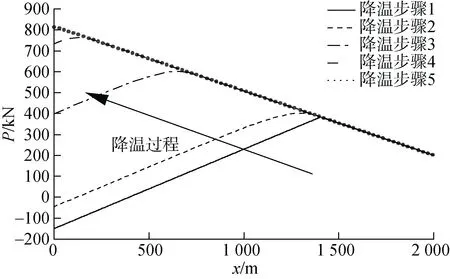
图12 方案1 卸载过程中有效轴力变化图Fig. 12 Effective axial force during the unloading of case 1

由图11 可知, 升温时, 管道由中点朝向两端膨胀, 方案1 由于采用了单向锚固方式, 升温时锚链不受力, 因此有效轴力在管道中部达到最大, 最大值为–333 kN; 方案2 由于采用了双向锚固方式, 管道在锚固位置移动量为0, 但有效轴力达到了–559 kN。降温时, 管道由两端向中点收缩, 方案1 与方案2 的有效轴力分布图相同。可见当热端收缩到初始安装位置时, 两种方案锚链均产生了拉力以限制管道继续收缩, 最大有效轴力均发生在锚固位置处, 约为814 kN。对比图7 可知, 锚固后的最大有效轴力显著增加, 增量为298 kN。

方案1 升温时锚链未对管道运动产生限制, 因此锚固力产生于降温过程, 由力的平衡条件可知, 锚固力为814 kN。而方案2 升温与降温过程锚链均限制了管道的移动, 升温时, 由1 号锚桩提供559 kN 拉力;降温时, 由2 号锚桩提供814 kN 的拉力。锚固力越大,对锚桩要求越高, 对工程安全越不利。由图12 可知,方案1 的卸载过程中锚链提供的阻力是逐渐增大的,直至锚的作用被完全激发达到最大值, 此时管道P也达到了最大值, PLET 端的收缩被完全限制。

图13 为方案3 及方案4 的P-x图。

图13 方案3 及方案4 有效轴力分布Fig. 13 Effective axial force profile of cases 3 and 4

图13 与图11 相似, 但是由于锚固位置的改变, 单向锚与双向锚在升温阶段均会发挥作用, 以限制管道朝向SCR 端的移动。而升温阶段管道内的有效轴力为压力, 过大的压力累积将导致管道发生整体屈曲。对比图13 与图11 可得, 在SCR 端锚固比在PLET 端锚固积聚的压力更大, 因此其发生整体屈曲的风险更高。

方案3 升温时锚链立即产生作用力限制管道移动, 由力的平衡可得, 管道在锚固处的锚固力应为SCR 张力与P之和, 即964 kN。而方案4 升温与降温锚链均提供力以限制管道移动, 升温时, 由1 号锚桩提供765 kN 拉力; 降温时, 由2 号锚桩提供608 kN 的拉力。

在端部进行锚固时, 有效轴力重新分布后, 往往由一端向锚固端逐渐累积, 直到在锚固处达到最大,由于累积路径较长, 锚固处的有效轴力往往很大, 而在中部锚固, 由于累积路径缩短, 可以解决有效轴力过大的问题。图14 为方案5 与方案6 的P-x图。

在中部锚固时管道有效轴力分布图与无锚固时(图7)管道有效轴力分布图相似, 都是由两端向中间逐渐累积, 在管道中部某一位置有效轴力达到最大,因此相较于在一端锚固, 中部锚固能显著降低有效轴力。由图14 可知, 管道最大有效轴向压力仍位于锚固处, 其值为457 kN。中部双向锚固与单向锚固得到的u-n图及P-x图相同。

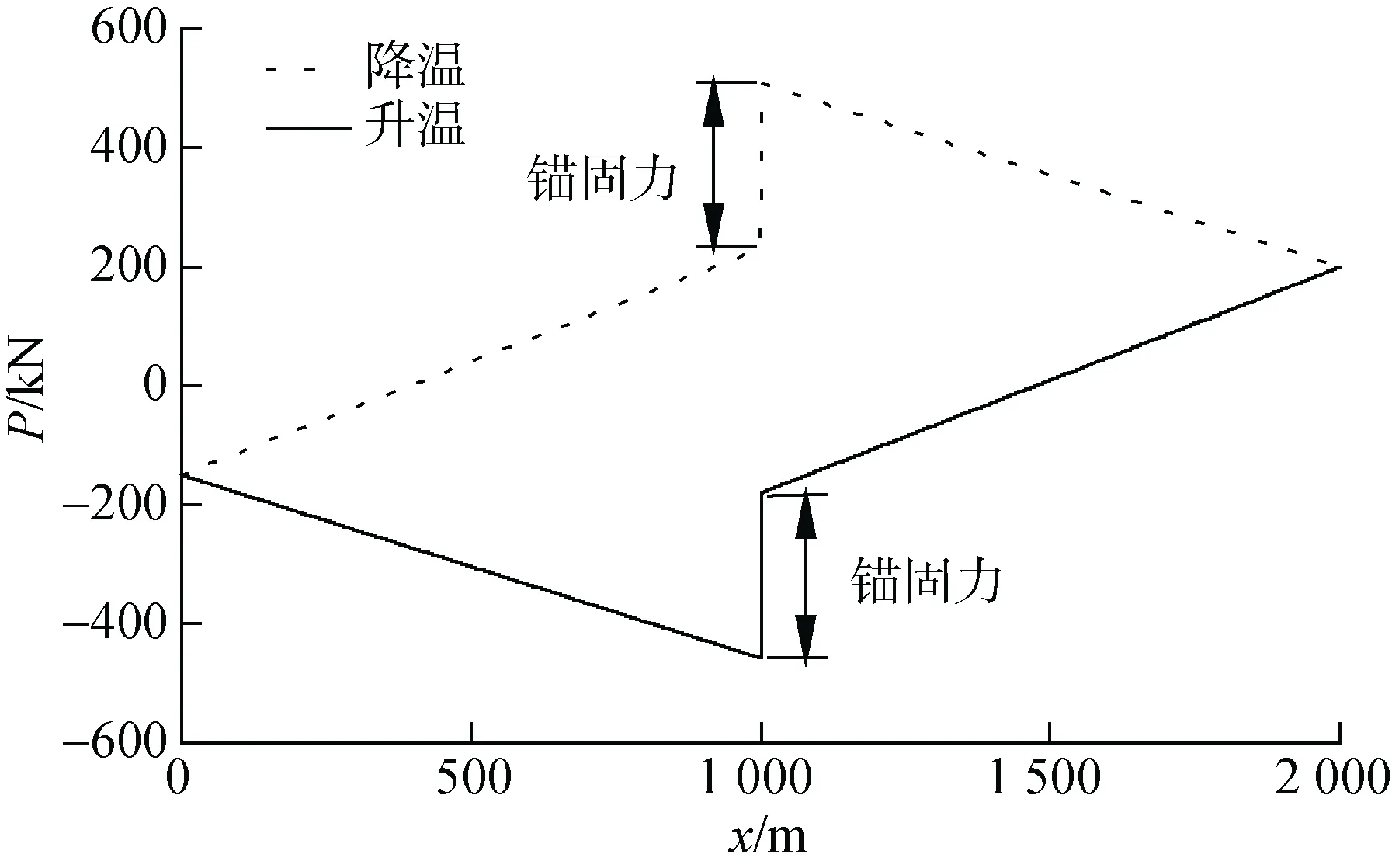
图14 方案5 及方案6 管道有效轴力分布Fig. 14 Effective axial force profile of cases 5 and 6

2.3 推荐的锚固方案

综合考虑SCR 端最大移动量、PLET 端最大移动量、最大锚固力Fanc,max、最大有效轴向压力Feff,max、有效轴向压力影响长度leff, 对以上6 种锚固方案进行比较, 见表2。

表2 锚固方案比较Tab. 2 Comparison of anchor cases

由表2 可知, 6 种不同的锚固方式对两端最大轴向移动量的结果影响较小; 但不同锚固方式对锚固力的要求不同, 端部锚固产生的锚固力约为中部锚固的2.8～3.5 倍。

综合考虑以上几方面因素, 在管道的中部锚固具有较大的优势。在中部锚固的单向锚与双向锚其锚固力与位移控制均具有同样的结果, 即使用双向锚是不必要的。因此可得出结论: 对于不考虑整体屈曲的短管, 方案5 为最佳锚固方案。

3 锚固与滑动基础的耦合

3.1 端部锚固耦合滑动基础

滑动基础在设计之初主要是解决“长管”膨胀与收缩问题的。海底管道因为启闭循环, 常常会出现明显的轴向膨胀与收缩, 而管道的端部结构例如PLET, PLEM 等由于具有较大的重量和面积, 导致与管道相比其受到的地基土体摩擦力更大。因此当管道运动受到端部结构的限制时, 会对管道系统施加相当高的负荷。滑动基础允许管端自由移动,可以有效地解决这一问题。管道轴向移动作为近年来新发现的安全问题, 在设计中往往被忽略。如果滑动基础设计没有考虑管道轴向移动, 那么管道系统将承受设计中没有预料的载荷。Thompson 等[14]对传统的滑动基础做出改动, 即将端部锚固与滑动基础联合以解决海管的整体轴向移动问题。滑动基础机构如图15 所示。

图15 带滑动基础的PLET 示意图Fig. 15 Sketch of the PLET sliding foundation

图15 中,L1用于管道受热膨胀时滑动基础的预留偏移,L2用于管道降温收缩时向中点的应急偏移。数值模拟中, 为模拟滑动基础与端部锚固耦合,L1=2.5 m、L2=1.0 m, 采用非线性边界条件。即当轴向移动在滑动基础设计的运动范围之内时, PLET 可以在基础上自由移动, 当PLET 移动到滑动基础端部并进一步发生位移时, 其位移将被完全约束。

图16, 图17 是一端为SCR, 一端为滑动基础的海底管道模型在启闭循环中的P-x图及u-n图。

分析图16, 图17 可得, 管道以每循环0.516 m的恒定速度向SCR 端移动, 直至在第三循环管道收缩时达到滑动基础右端端部, 此后管道整体移动被限制, 每循环升温过程有效轴力不变, 但降温过程的有效轴力不断增加, 直至n=5 时有效轴力趋于稳定, 最大值为808 kN。

图16 带滑动基础的管道有效轴力分布Fig. 16 Effective axial force profile with the sliding foundation

图17 带滑动基础的管道两端轴向移动量-循环曲线Fig. 17 Walking vs. cycle with the sliding foundation

3.2 中部锚固耦合滑动基础

虽然锚链系统能较好地控制管道的整体移动, 但显著增加了管道的有效轴力; 滑动基础能够在一定程度上放开对位移的限制, 从而降低管道的有效轴力。将二者相结合并选用前述最佳锚固方式即在管道的中部锚固端部采用滑动基础。图18 为锚链系统与滑动基础联合方案与只在中部单向锚方案的管道两端轴向移动量-循环对比图, 图19 为有效轴力对比图。

图18 管道两端轴向移动量-循环曲线Fig. 18 Walking vs. cycle

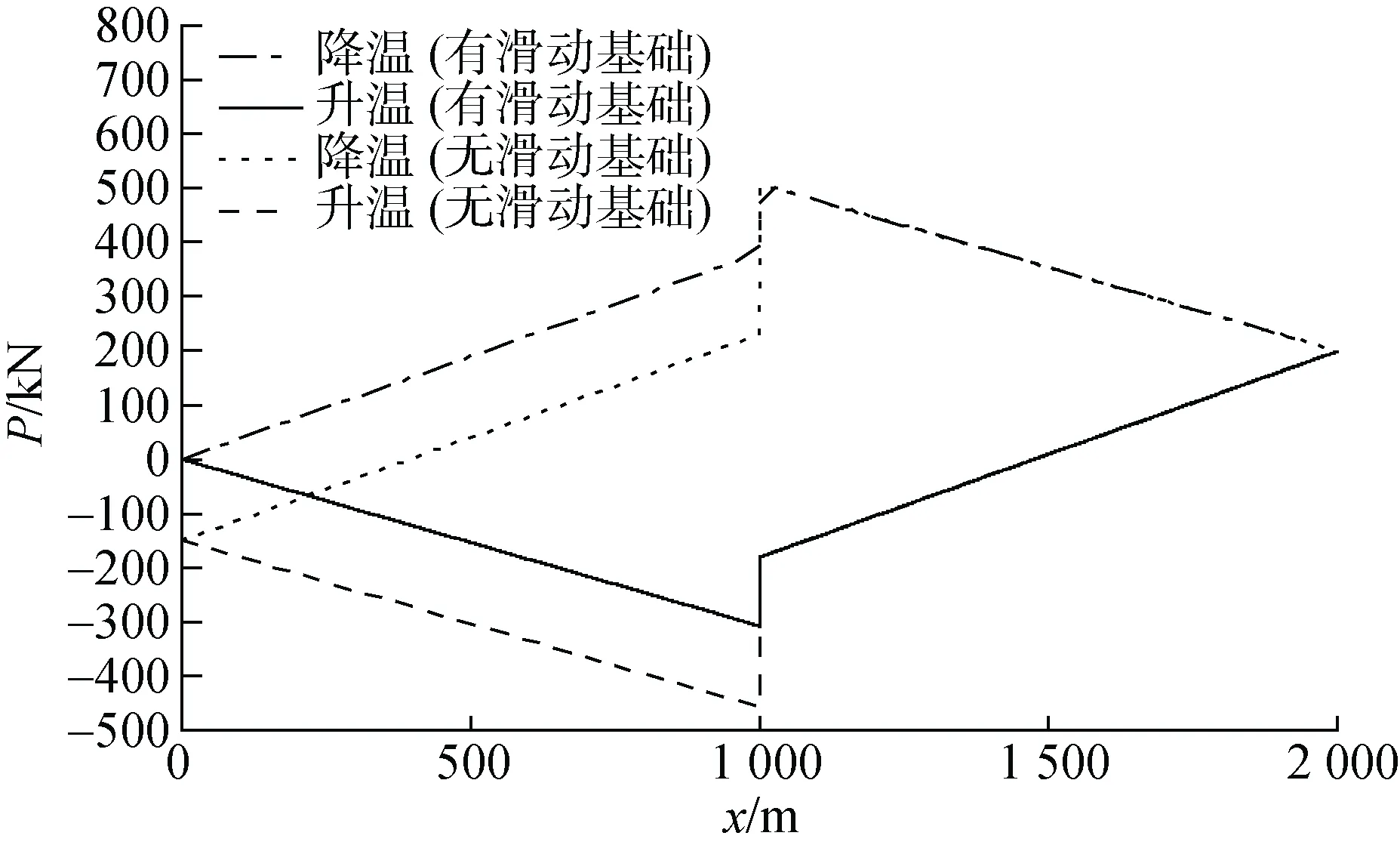
图19 管道有效轴力分布对比Fig. 19 Comparison of the effective axial force

如图18, 两种方案位移差别很小。但由图19 所示两种方案有效轴力分布差别较大。采用滑动基础时锚固力约为127 kN, 管道中的最大有效轴向压力为307 kN; 而无滑动基础时, 锚固力约为278 kN,管道中最大有效轴向压力为457 kN。因此, 相较于仅在中部锚固的情况, 锚链系统与滑动基础相结合可以有效降低锚固力和有效轴向压力, 是最佳的消减管道轴向移动量的方法。

4 结论

本文研究了2 km 长的海底管道一端连接SCR,另一端连接PLET 时轴向整体移动的消减方案, 确定了最佳锚固点及锚固方式, 分析了滑动基础对消减轴向移动的作用。具体结论如下: (1)相较于海床坡度和瞬态热梯度等诱发因素, SCR 张力对海管轴向整体移动的影响更为显著。(2)对管道进行锚固能较好的消减管道轴向整体移动量。但不同的锚固方式所需的锚固力大小不同且显著影响管道内部的轴力分布, 研究提出最佳锚固点宜设置在管道的中部并采用单向锚固方式, 与其他锚固方式相比, 所需的锚固力可降低64%～71%。(3)采用滑动基础与锚桩刚性连接的方式能有效解决短管轴向移动问题。滑动基础能显著地降低管道有效轴力。在中部单向锚的基础上, 两端增加滑动基础能进一步减小锚固力与有效轴向压力, 所需锚固力降低了54%, 最大有效轴向压力减小了33%, 因此对于不易发生整体屈曲的短管, 端部采用滑动基础中部采用锚桩锚固的方式最为适合。