砾石单元法与SPH 耦合模型在数值波浪水槽中的应用研究
2020-10-09李彦卿别社安李大鸣
李彦卿, 别社安, 李大鸣, 王 鑫
(1. 天津大学 水利工程仿真与安全国家重点实验室, 天津 300072; 2. 国家海洋技术中心, 天津 300112)
光滑粒子动力学 (Smoothed Particle Hydrodynamics, 简记为SPH)方法是一种处理大变形边界运动问题的有效方法。20 世纪70 年代为研究天体运动的物理问题, Gingold 与Monaghan 提出了用追踪粒子的方法描述宇宙天体中星云的运动过程[1]。1992 年Monaghan 将SPH 方法扩展到求解不可压缩流体的大变形运动问题[2]。其后许多学者在SPH 的应用中做了多方面研究[3-6]。离散单元法(Discrete Element Method, 简记为DEM)最早是由Peter Cundall 博士于1971 年提出的[7-8]。DEM 的基本思想是利用一系列离散的粒子来模拟固体介质, 其中每个粒子为一个单元,具有固定的大小和形状, 粒子与粒子之间可以在小范围内相互挤压重叠从而产生相互作用力, 在通过牛顿运动定律计算出粒子的运动参数, 模拟固体介质的运动情况。近年来SPH-DEM 耦合模型也有新的研究成果[9-11]。SPH 与DEM 同时离散为粒子时, 两者颗粒尺度相当, 只是在颗粒性质上有区别[12]; 当SPH 离散为粒子, DEM 用组合形式表示固体物面时, 主要描述大尺度、数量不多、结构形式确定(可以有一定变形)、具有独立运动(一般为悬浮)的固体物面。对堆积砾石来说,与SPH 流体粒子尺度不同, 堆积砾石数量较多, 砾石轮廓形式复杂(可以统一模化), 堆积砾石相互挤压、遮挡运动相互制约。为解决堆积砾石的群体运动问题, 本文提出了砾石单元法(Gravel Element Method, 简记为GEM), 建立了单砾石近似为力学球的概念, 用球度系数和形状系数对砾石几何形态进行近似; 对于不规则的砾石轮廓, 用傅里叶级数展开砾石边界轮廓, 将砾石表面的力学特征赋予在周期函数变化的展开函数中,在力学球形态的砾石表面增加对应非球形砾石位置处的滚动摩擦阻力系数、滑动摩擦阻力系数和转动惯量分布。研究了有级配非圆形状颗粒对给定坝型的随机填充方法, 对堆积砾石力学球的受力状态进行了分析,提出了拟序排列、分级求解和静力传递的方法。建立了SPH-GEM 耦合波浪水槽和堆积砾石塌落、滚落的数学模型。
1 堆积砾石的受力分析
1.1 单砾石几何形态
假定砾石颗粒内部密度均匀, 在边缘轮廓线段的基础上, 可以求出砾石颗粒投影平面θ上的图形形心(xc, yc), 以形心为极点, 可以确定颗粒边缘轮廓曲线的极角φ和极坐标半径R, 颗粒边缘轮廓线的半径以T=2π 为周期循环变化, 可以表示为R(θ, 2π+φ)=R(θ,φ)。
理论上讲砾石颗粒具有三维特征, 可以在球坐标中将砾石的任意切面以平面坐标展开, 足够的切面组合可以描述砾石的三维特征, 研究任意切面上砾石的轮廓则具有二维特征。
对不规则的砾石轮廓, 在θ平面上用傅里叶级数来逼近周期函数R(θ,φ), 得
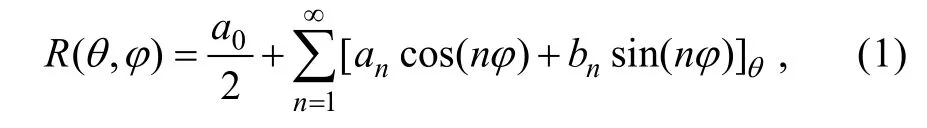
式中:n=1, 2, 3, ...为级数的各项级数;a0为常数项, 表示颗粒投影平面上的平均粒径;an和bn为傅里叶级数各项系数, 表示在平均粒径基础上的半径修正量。
傅里叶系数由以下公式确定
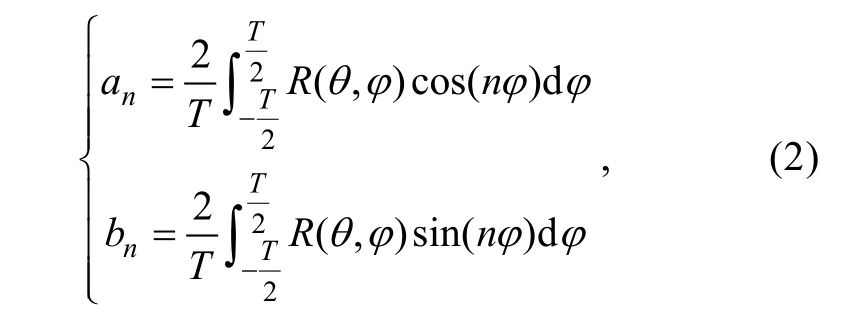
当an和bn均为零时, 砾石颗粒半径为,a0为圆形砾石。低频谐波(n较小)反映砾石颗粒表面较大尺度的形态变化, 高频谐波(n较大)反映砾石颗粒表面较小尺度的形态变化。谐波越多, 傅里叶级数生成的轮廓线越接近于实际砾石颗粒的轮廓线。图1a 为砾石颗粒的图像采集, 图1b 为砾石颗粒的轮廓模拟。
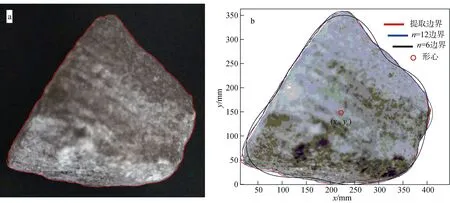
图1 砾石颗粒图像和轮廓模拟Fig. 1 Image of gravel particles and contour simulation
砾石与球体的偏离程度可以用球度系数和形状系数来描述[13], 球度系数公式为[14]
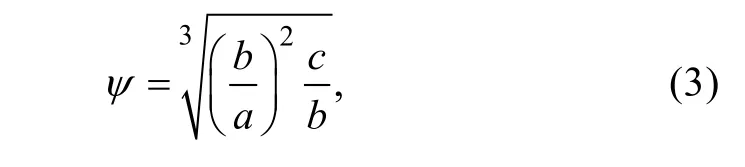
式中:a为砾石长轴;b为砾石中长轴;c为砾石短轴。
形状系数公式为[14]
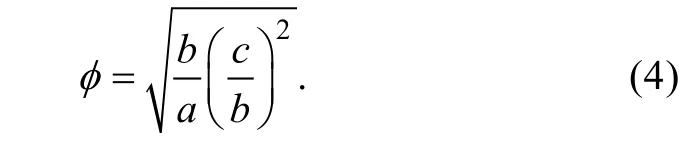
对退化的二维砾石颗粒, 可以假定c=b。对二维砾石颗粒, 引用公式(1)中傅里叶级数各项系数an、bn作为傅里叶级数各级砾石的长轴和中长轴, 可以将非圆颗粒形状用数个圆颗粒部分表面的组合形状来近似(图2)。砾石的二维圆周矢量半径展开曲线为图3。
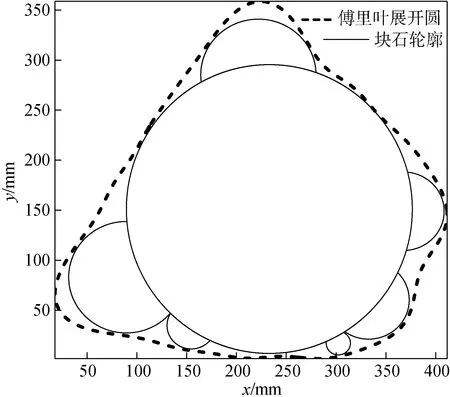
图2 非圆颗粒的组合形状Fig. 2 Combined shape of non-circular particles
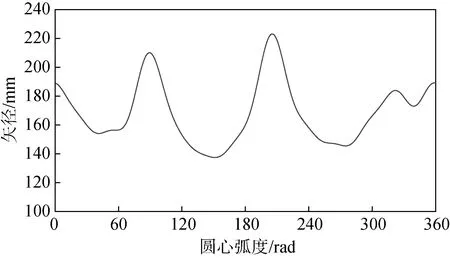
图3 砾石的二维圆周矢量半径分布Fig. 3 Distribution of the 2D circumferential vector radius of the gravel
1.2 单砾石力学球概念
通过考察不同投影平面的砾石傅立叶级数各级系数半径, 可以得到砾石的球度系数或形状系数,不仅从砾石表面整体上获取砾石对球的近似程度,而且可以对不同位置的球面近似形态进行描述。可以将泥沙颗粒的球度系数延伸到砾石的球态研究中,表1 为砾石几何形状与球度系数的关系。
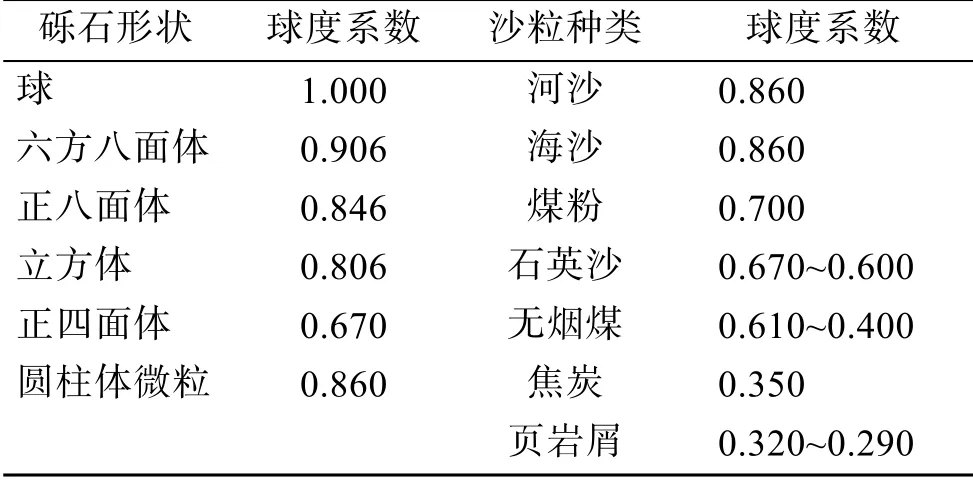
表1 砾石几何形状与球度系数的关系Tab. 1 Relationship between gravel geometry and sphericity coefficient
用球体近似砾石不仅是通过球度系数对砾石形态的形似, 而且要赋予球表面上砾石的力学性质。球形砾石容易滚动, 与其他球形颗粒主要为点接触,表面相对阻力较小, 具有较均匀的表面摩擦力和不变的转动惯量。而非球形砾石的棱角有时会阻碍滚动, 有时会使颗粒迅速翻转, 在各部位转动惯量不一致, 局部较平缓粗糙的表面会增加表面摩擦力。为达到用球形砾石模拟非球形砾石运动的目的, 引入力学球的概念, 即当球形砾石与非球形砾石的力学特征相同时, 这种球形砾石称为力学球。
力学球以球的形状存在, 用球度系数作为砾石与球体的形状修正系数, 在球形砾石表面增加对应非球形砾石位置处的滚动摩擦阻力系数、滑动摩擦阻力系数和转动惯量分布, 这样就可以达到用球形砾石模拟非球形砾石运动的效果。这在理论上完全可行, 但在实际操作中面对数量较多、表面复杂的堆石工程来说, 不可能对每一砾石颗粒进行表面测量和轮廓模拟。但可以选择有代表性的砾石, 采集砾石表面轮廓特征, 确定力学球表面的样本函数, 引入随机分布的力学函数来近似解决这一问题。
力学球的滑动或滚动摩擦的阻力系数可以表示为
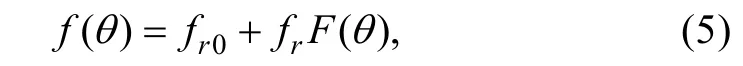
式中:fr0为球面滑动或滚动摩擦系数;fr为非球面平均滑动或滚动摩擦系数;F(θ)为随θ变化的随机函数。
力学球的转动惯量可以表示为
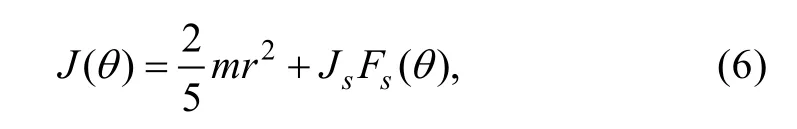
式中:Js为非球面平均转动惯量;Fs(θ)为随θ变化的随机函数。
1.3 堆积砾石的受力状态
堆积砾石表层石块所受到的作用力会通过接触压力、反力、碰撞传递给其它砾石, 使砾石进入运动状态或达到新的平衡状态。堆积砾石受力见图4, 力学球砾石堆见图5。
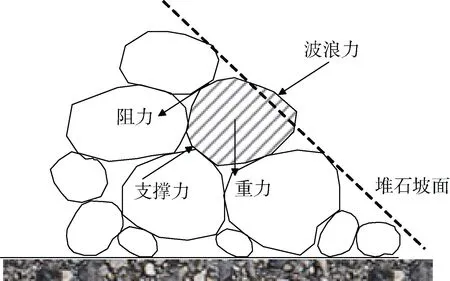
图4 砾石受力示意图Fig. 4 Gravel strength diagra m
可以看出内部砾石除自身重力外, 还有砾石上面的压力作用, 和下面砾石的反力。显然要研究每一砾石的受力情况必须从外层砾石颗粒入手。为求解每一力学球上的受力, 可以由外及内逐次递进对力学球上的作用力进行求解, 求解顺序显得尤为重要。需要根据求解层次进行重新编号, 将这种重新编号的过程称为拟序排列过程, 图6 为按求解层次编排的级别号, 图7 为按级别求出的压力分布。
当取直径d=1.0 m, 密度与重力加速度乘积ρg= 2 650 kg/m2s2。按球体计算, 累加球体重力为321 745.344 88 N, 通过传递力模式计算的地面总反力为321 745.344 08 N, 工程上并不需要如此精度的数值,这里主要是为验证传递力模式计算结果的可靠性; 同时地面给予力学球的摩擦力为193 047.2 N, 以保证堆积球体不滑落。
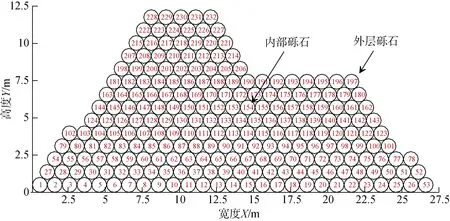
图5 力学球砾石堆Fig. 5 Mechanical ball gravel pile
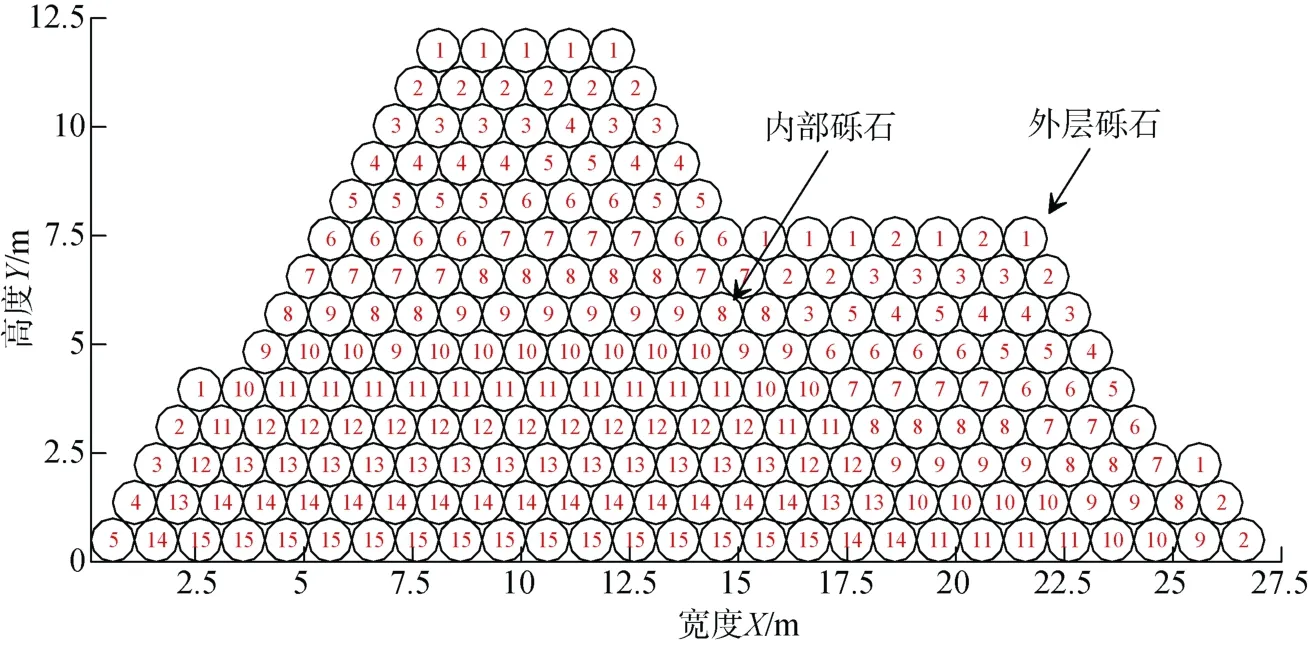
图6 按求解层次编排的级别号Fig. 6 A level number organized by the solution level
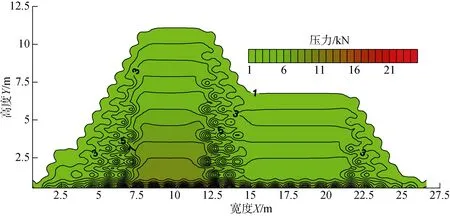
图7 按级别求出的压力分布Fig. 7 Pressure distribution by grade
2 砾石单元法(GEM)
2.1 GEM 模式
GEM 是以独立的砾石整体作为一个刚性单元,砾石表面的轮廓线是单元边界, 砾石以整体运动,具有平动和转动的形式。砾石间可以通过接触传递力和力矩, 具有运动速度的砾石可以传递动量。在GEM 模式中引入力学球的概念, 不考虑砾石的形状变化; 力学性质可以分布在力学球表面, 使力学球具有静、动摩擦系数, 不同表面位置具有不同的转动惯量。力学球之间不能压入和穿越, 运动受拟序排列控制, 将砾石刚体碰撞效果代替微弹性假定, 力用接触压力和反力模拟, 力矩用接触摩擦和重力对支撑点之矩模拟[15-16]。运动受力球动力传递模式如图8所示。
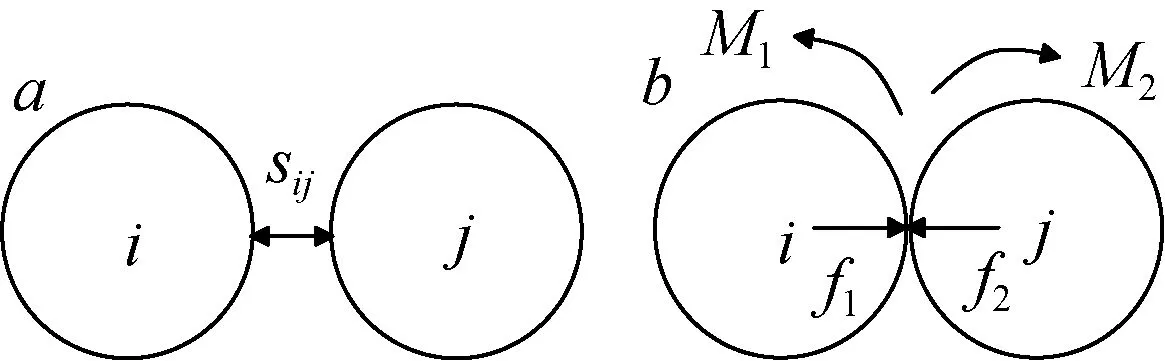
图8 砾石力学球动力传递示意图Fig. 8 Schematic of the dynamic ball transmission of gravel mechanics
砾石的运动模式主要有塌落、平移、滚落、碰撞和跳跃。作用力较小或砾石较大时平移和跳跃不容易发生, 塌落和滚落是两种主要的运动形式, 碰撞处理为力的传递。
2.2 GEM 主要力学公式
在碰撞过程中力的传递是以与位移和速度的形式表达力的传递, 可以表示为
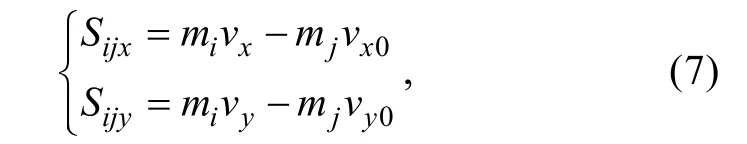
式中:Sx,Sy分别为砾石传递的冲量;vx,vy为位移速度;mi,mj为砾石质量。
根据力的合成原理, 砾石受到的合外力Fi以及合外力矩Ti为:
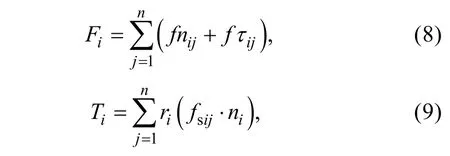
式中:n为砾石颗粒i相接触的颗粒j的数量;fs为颗粒间的滑动摩擦力;ni和iτ 为砾石轮廓线处的法线和切线的单位向量。
力和力矩传递表示为
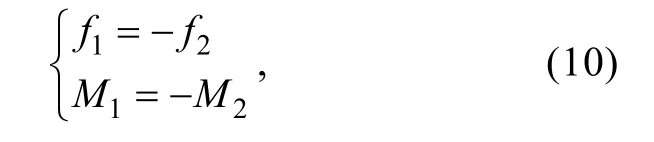
式中:f1,f2表示接触力;M1,M2表示接触力矩。
砾石间的不嵌入条件为
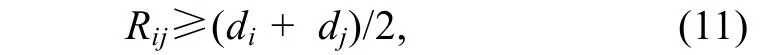
式中:Rij表示力学球心间的距离;di,dj表示两力学球的直径。
2.3 GEM 与DEM 比较
GEM 与DEM 主要有以下几点不同:
(1) 砾石单元法以砾石为整体刚性单元, 主要以硬球的接触模式为主, 忽略砾石表面的变形细节; 离散单元法以粒子形式分布单元, 主要考虑软球模式的接触方式, 把颗粒间的法向力简化为弹簧和阻尼器。
(2) 砾石单元法以堆积砾石为研究对象; 离散单元法可以模拟固体颗粒群的运动, 一般不考虑砾石承压和遮蔽引起的运动次序的差别。
(3) 砾石单元法是在堆积砾石稳定性研究基础上提出来的, 在力学模式上具有外部失稳但内部稳定的物理意义; 离散单元法以模拟固体颗粒群体运动的效果为基础, 具有整体失稳的物理意义。
3 SPH 与GEM 耦合波浪砾石模型
3.1 SPH 波浪水槽模型及其控制方程
采用SPH 方法, 建立了波浪水槽的数值模型, 水槽由底部和右侧的固壁边界及左侧的造波推板边界组成, 其内部填充流体粒子。水槽初始水位为0.4 m,粒子初始间距为0.01 m, 光滑长度取3.2 倍的光滑长度取3.2 倍的粒子初始间距。
SPH 控制方程严格遵循质量守恒、动量守恒及能量守恒这三条物理守恒定律, 将描述流体运动的Navier-Stokes 方程, 通过SPH 法基本理论的思路对N-S 方程进行空间离散化, 得到了在笛卡尔坐标系下并且适用于广义流体动力学的SPH 控制方程。SPH中最常用的连续方程粒子近似式为:
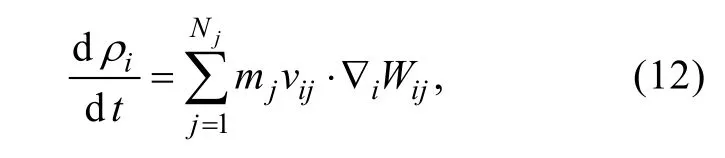
式中:m为粒子质量;ρ为粒子密度;v为粒子速度;W为粒子核函数; 下标i和j为粒子编号;Nj为光滑长度内粒子数量。
根据以上连续方程可知, 粒子密度变化率与所求粒子与其相邻粒子的相对速度有关。
在SPH 方法中, 带有层流黏性项的动量守恒方程为:
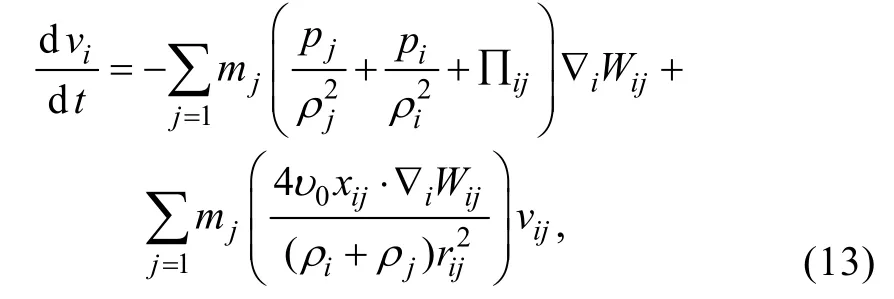
式中:p为压强;v0为黏性系数;x为坐标分量。
在SPH 的计算中, 流体被认为是弱可压缩的。这便于使用状态方程来确定流体压力, 这比求解泊松方程等方程要快得多。SPH 的状态方程为:
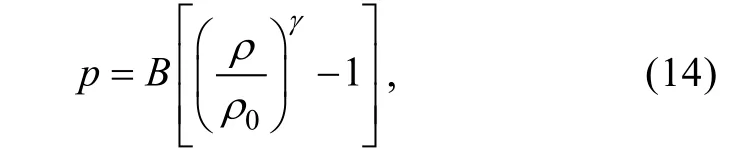
式中:γ为常数, 在大部分情况下取7; ρ0为参照密度,通常为1 000 kg/m3,B为参数用于限制密度的最大改变量, 在本文中为在参考密度下的声速。
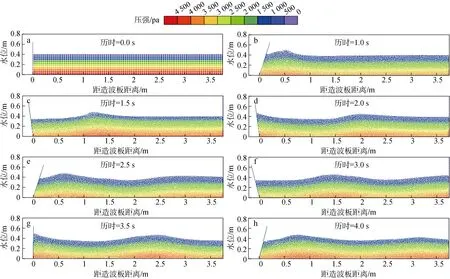
图9 数值波浪水槽模拟的造波过程和压力分布Fig. 9 Wave-making process and pressure distribution simulated using the wave numeric channel
图9 为波浪水槽造波过程和压力分布, 波浪周期取1.2 s, 输出数据的时间间隔为0.01 s, 总共输出4.5 s。模型计算由0.75 s 到1 s 的时间间隔内, 产生第一个大波, 此时刻波峰位置为距造波板0.5 m 左右,并持续向另一侧边壁移动。 在模型计算由1 s 至1.25 s的过程中, 造波板经由右侧最大摆幅处开始向回运动, 此时波峰运动到距造波板0.8 m 处。波峰左侧的流体粒子都拥有向右侧运动的加速度, 而由于造波板回移导致其附近处水面塌落, 波谷开始形成。在模型计算的1.25 s 至1.5 s 的过程中, 造波板完成一个造波周期, 波峰位置移动到距造波板1.2 m 处, 波谷位置仍处于造波板附近。其后, 在模型计算的1.5 s至3.0 s, 造波板重复此前的运动过程。
建立物理模型试验, 对数值模拟结果进行验证分析。数值波浪模拟结果如图10 所示, 为周期1.2 s的波浪数值模拟变化与实测波浪数值测试。由图10中可以看出, 当数值波浪模拟由初始时刻开始到达稳定状态后, 数值模拟与实测波浪模拟结果较吻合。
3.2 SPH 与GEM 耦合模型数学基础
SPH 与GEM 耦合模型由SPH 粒子和堆积砾石构成, SPH 粒子运动由方程(12)控制, 堆积砾石处为SPH 粒子的固体边界, SPH 粒子运动速度为
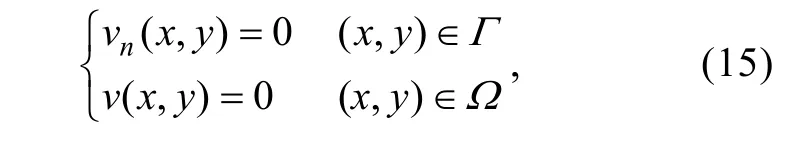
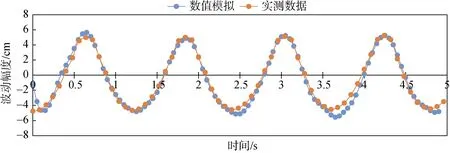
图10 波浪水槽数值模拟与实测数据对比Fig. 10 Numerical simulation of the wave channel compared with the measured data
式中,Г表示砾石表面;Ω表示砾石内部;n表示砾石表面法线方向。
SPH 粒子对砾石的作用力为沿砾石表面的法线方向压力的积分, 利用势流的伯努利方程为
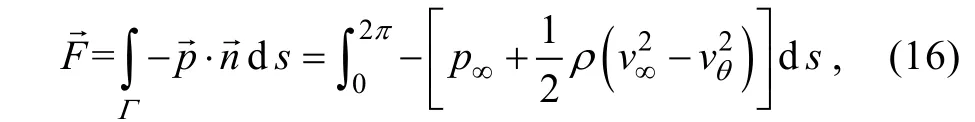
式中,p∞表示砾石表面;vθ表示砾石表面切线方向速度;n表示砾石表面法线方向。
砾石运动轨迹方程为
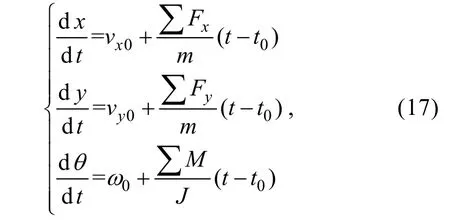
式中,vx0,vy0,ω0分别为砾石在计算时段初始t0的运动速度和角速度; ∑Fx, ∑Fy,∑M表示砾石所受的合力和合力矩;J表示砾石的转动惯量。
砾石间力的传递由公式(7)至公式(10)确定。
3.3 SPH 与GEM 耦合模型模拟过程
SPH 与GEM 的耦合过程主要有以下几点:
(1) 应用坝体轮廓线控制将具有级配的堆积砾石随机放置在SPH 数值水槽中, 确定每一块砾石轮廓线内受控制的SPH 粒子, 这些粒子称为受控粒子,不包含SPH 粒子的砾石是水面以上砾石或尺度较小的砾石, 不包含SPH 粒子的砾石不会影响砾石运动计算模拟。受控粒子与非受控粒子分布见图11。
(2) 在SPH 模型边界上使用推板造波, 砾石中的受控SPH 粒子参与核函数计算, 但运动速度为零,相当于将砾石对周边SPH 粒子的影响分解为受控粒子对周边SPH 粒子的影响, 体现了砾石边界轮廓对SPH 模式的耦合效果。
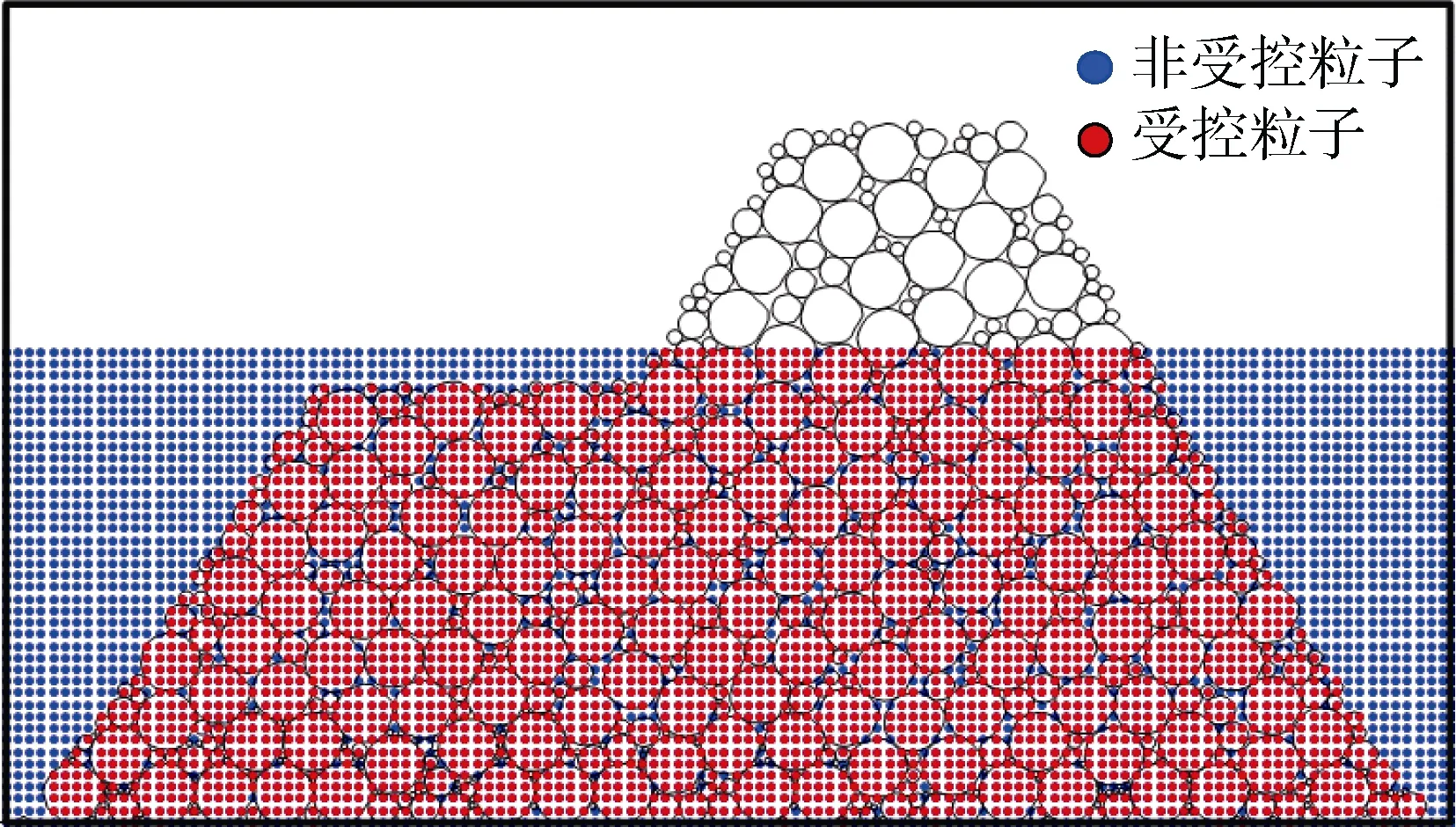
图11 受控粒子与非受控粒子分布Fig. 11 Distribution of controlled and uncontrolled particles
(3) 同步统计砾石的受力和周边的流速场影响(见图12), 砾石受到的总压力可以用砾石中受控粒子的总压力代替, 受控粒子(图12 黑轮廓线内粒子)的压力分布决定了砾石运动形态。砾石周边流场取砾石轮廓以外、砾石光滑长度以内的粒子做统计分析, 图12 中黑色砾石轮廓外与红色光滑长度圆内的粒子, 黑色矢量表示砾石光滑长度, 本文取2 倍的力学球半径, 这一区域的流速、流向可以处理为波浪对砾石的冲击效果, 砾石是否进入运动状态, 这也是重要判别条件之一。
(4) 在堆积砾石的受力分析中, 用拟序排列、虚位移原理确定砾石的承压力、反力、摩擦力和挤压力, 确定砾石进入运动状态的级别, 通常级别的确定会在每次计算前重新划分, 因为每一次砾石运动都会改变砾石堆的排列形式, 一般一次计算中只需考虑1 级砾石的运动, 其他级别得不到运动的机会。
(5) 波浪力不足以撼动砾石时, 砾石保持原有状态; 波浪力撼动砾石时, 要考虑砾石的反力分布确定砾石运动形式, 一般情况为没有反力作用时为塌落, 有支撑点时要找出支撑点砾石。
(6) 砾石运动和就位应在瞬时完成, 所以在一个时间步长内就应当确定出砾石运动后的位置, 这一位置应避免与其它砾石压入, 并位于砾石运动的路径上;砾石进入新的位置后将会放弃以前的受制粒子, 同时产生出新的受制粒子, 完成了一个计算的循环过程。
3.4 SPH 与GEM 耦合模型模拟结果
应用SPH-GEM 方法耦合的数学模型来模拟波浪作用下防波堤模型由静态平衡到动态平衡的变化过程。防波堤模型在数值波浪的作用发生改变, 边坡部分计算颗粒滑落, 但流体粒子仍正常穿越砾石边界之间的孔隙参加运动。数值模拟波浪水槽水深为0.4 m,波高为0.10 m。防波堤模型选取坡度为1︰1.5, 肩台高0.4 m, 堤顶高0.6 m。图13 展示了计算模型随时间的变化。当模型计算由初始0 时刻到3 s 的过程中, 造波程序生成波浪并传递至防波堤模型, 并开始于防波堤模型进行相互作用。当模型由3 s 至4.5 s 的计算过程中, 由于波浪作用导致防波堤模型的边坡粒子部分滑落并于坡面下部堆积。当模型计算由4.5 s 至5 s 的计算过程中, 防波堤模型达到稳定状态。由图可见在计算时刻为5 s 的防波堤模型, 其断面形状已经达到反S 的形状。
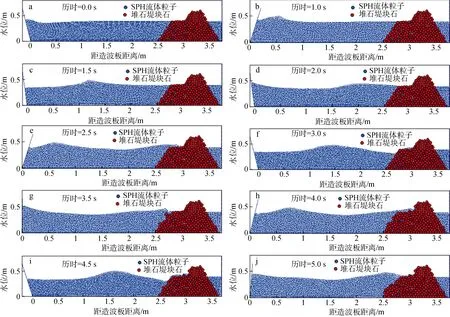
图13 防波堤模型坡面颗粒变化过程Fig. 13 Process of changing the grain slope in the breakwater model
图14 为防波堤模型初始状态, 图15 为防波堤模型稳定状态, 图16 为最终断面平衡对比图。防波堤模型砾石的最终动力平衡断面为反S 形状。
3.5 耦合模型的可靠性验证
为了进一步验证数值模型结果的可靠性, 采用本文数值模拟方法对文献[17]中的物模结果进行验证分析。模型选取的水槽长度为5 m, 水槽高度为0.8 m, 对应的水深为15 cm, 波高为5 cm, 周期选择1.5 s。以SPH 方法生成的初始流体粒子间距为0.01 m。防波堤物理模型的对应位置及测点位置如图17 所示。防波堤模型选取粒径为6 cm 左右的单一介质, 坡面角度为1︰1.5, 堤顶高30 cm, 堤顶宽10 cm, 模型的孔隙率约为0.35。图18 为数值模型的计算示意图。根据文献中的物理模型实验结果, 分别对4 个测点位置的波高数值进行验证分析。
对比模型的计算数据与文献中的试验数据发现波高数据基本吻合, 见图19。但是波浪模型的计算仍然存在误差, 考虑由于水深和波高都较小导致流体粒子的运算受到影响, 并且由于流体粒子的黏性系数考虑波高不能与实验数据完全吻合。
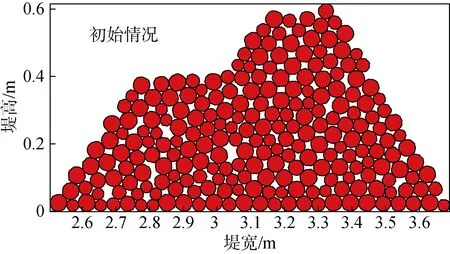
图14 防波堤模型初始状态Fig. 14 Initial state of the breakwater model
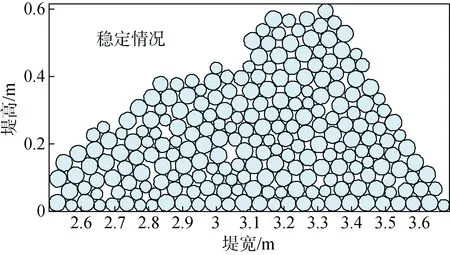
图15 防波堤模型稳定状态Fig. 15 Steady state of the breakwater model
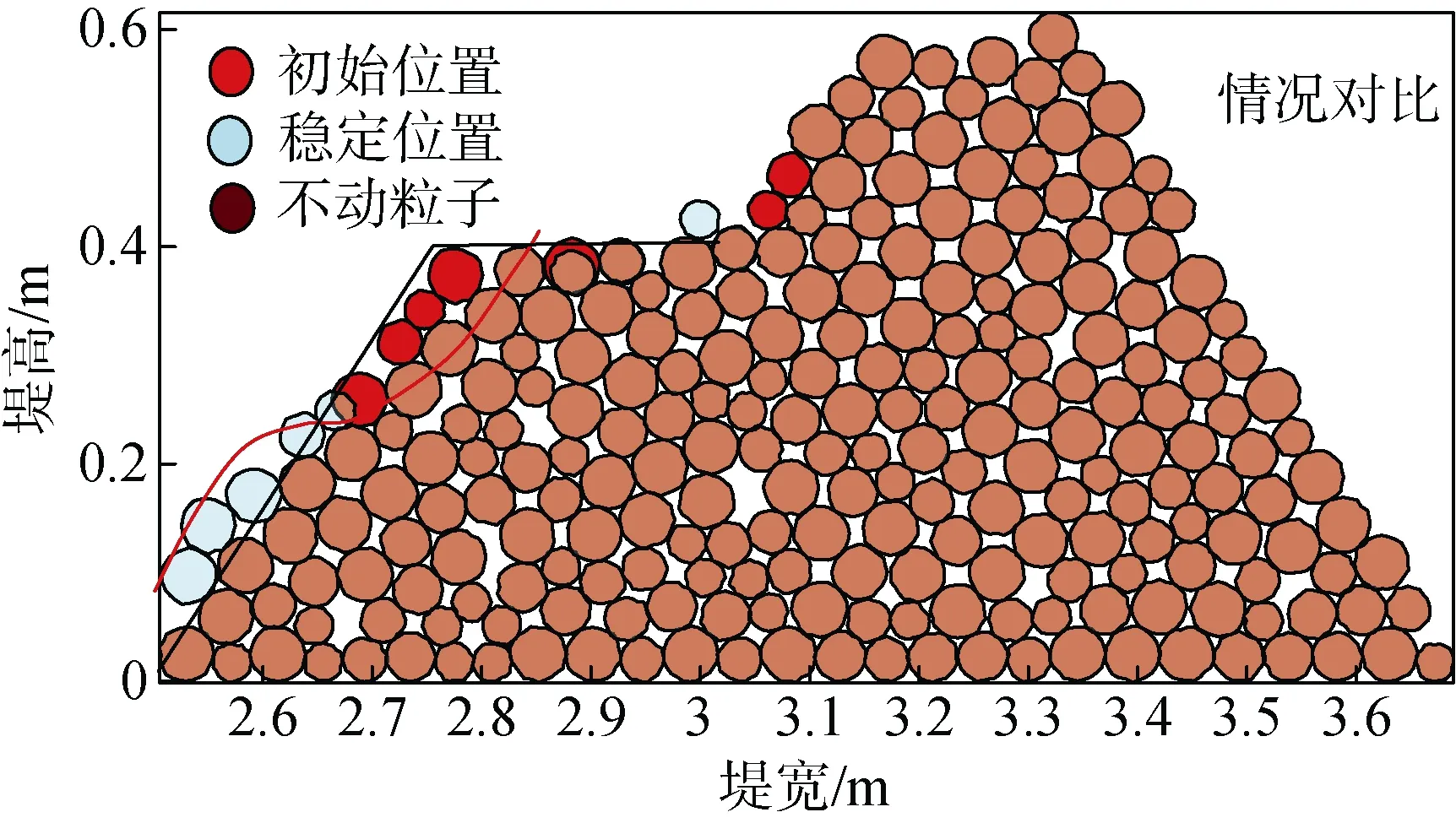
图16 防波堤模型断面变化对比Fig. 16 Comparison of the cross section of the breakwater model
4 波浪砾石物理模型试验
4.1 物理模型试验
物理模型试验在天津大学北洋园校区港口航道与海岸工程实验室的小水槽进行。试验水槽长35 m,宽1 m, 高1 m, 模型距离造波板28 m, 造波机为天津理工大学制造的AFM-124 型造波机, 该造波机可根据试验条件需求产生规则波与JONSWAP 谱的不规则波, 由计算机系统控制运行。试验波浪参数的测量与分析, 由中国水电科学研究院制造的波高仪、压力传感器和SG-800 型水工模型试验数据采集与处理系统完成, 流速测量采用声学多普勒流速仪Vectrino-II,试验过程由计算机进行数据输入、输出、和处理。波浪试验水槽见图20。

图17 文献实验布局示意图(单位: cm)Fig. 17 Literature experiment layout

图18 数值模型计算示意图Fig. 18 Schematic of the numerical model calculation
试验断面和设备分布如图21, 堤顶高程为50 cm,堤顶宽度为20 cm, 肩台高程为42 cm, 肩台宽度为25 cm, 迎波堤面坡度为1︰1.5, 肩台处及迎波面砾石护面层厚度为10 cm, 堤顶处砾石厚度为8 cm, 背波堤面坡度为1︰1.5, 背波堤面砾石护面层厚度为5 cm。
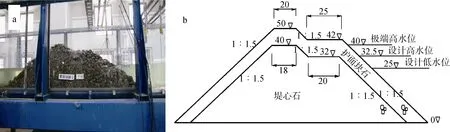
图20 波浪试验水槽Fig. 20 Experimental wave tank

图21 试验设计断面和试验设备在水槽中的分布Fig. 21 Test design and distribution section of the test equipment in the water tank
4.2 物理模型试验结果
图22 为在1 号点处物理模型的波浪观测值与数学模型模拟值的比较。可以看出物理模型造波平稳、波高变化较小, 数学模型造波周期稳定, 但波高起伏较大。因数学模型选取的粒子有限, 在波高处粒子相对少一些, 会影响波峰模拟的精度。但总变化趋势相同, 平均波高接近, 说明数值波浪水槽模拟成果基本正确。
图23 为在极端水位+ 40 cm 高程, 周期1.2 s, 波高H=10 cm 的规则波作用下, 波浪对坡面的冲刷区间开始上移, 整个+42 cm 高程肩台都在冲刷范围内。+42 cm 高程肩台在波浪的作用下迅速被冲刷并坍落。在持续波浪作用下, 肩台被冲刷的范围相比设计低水位及设计高水位有明显变化。当波浪持续作用200 个波后, 断面模型达到最终动力平衡状态。整个+42 cm 高程肩台被冲刷掉约7 cm 左右。坡面最大冲刷厚度约为4 cm, 冲刷滑落的块石在坡面下部堆积约4 cm, 部分块石滑落至坡脚并堆出近3 cm 左右的宽度。整个冲刷断面呈明显反S 形, 与数学模型结果变化趋势一致。

图22 波浪观察与波浪模拟的过程比较Fig. 22 Comparison between wave observation and wave simulation
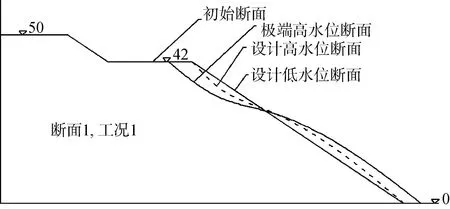
图23 防波堤断面1 模型试验工况1 动力平衡断面Fig. 23 Section 1 of the breakwater model test Condition 1 dynamic balance section
5 结论
(1) 采用傅氏级数的方法对块石轮廓进行了曲线展开, 说明块石轮廓沿曲线的矢径分布情况, 通过分布砾石轮廓上力学性质, 可以对砾石轮廓赋予力学上的摩擦系数、转动惯量等物理量, 提出了力学球体的概念。
(2) 分析了堆积砾石的受力特点, 提出堆积砾石分级方法和拟序排列求解方法, 对静态砾石堆应用拟序排列求得的解, 与理论值误差很小, 说明拟序排列求解方法可行。
(3) 提出了GEM 模型方法, 建立了SPH 波浪水槽与GEM 堆积砾石耦合数学模型, 模拟了砾石在波浪作用下的堤坝变形过程, 模拟结果与物理模型试验结果基本一致。
