基于1-D CNN的QRS波群检测算法

郭新杰，曾 成+，孙尚云，赵 地，花中秋

(1.河北工业大学 电子信息工程学院，天津 300401；2.中国科学院 计算技术研究所天津分所， 天津 300380；3.中国科学院 计算技术研究所，北京 100190)

0 引 言

近两年，卷积神经网络逐渐被应用于QRS波群检测。Marko等[1]提出了一种基于一维卷积神经网络(one-dimensional convolutional neural network，1-D CNN)的QRS波群检测算法，除去信号中的基线漂移后进行归一化处理，然后，选取包含145个采样点的滑动窗截取数据，若窗口中心距R波峰小于40 ms就作为正样本，否则为负样本，最终将1-D CNN模型的正输出做聚类以形成最终的QRS波群检测结果，准确率达到99.75%。Yande Xiang等[2]将基于注意力的二级1-D CNN方法用于QRS波群检测，首先通过数据预处理得到心电信号的差分信号和平均差分信号，然后，将不同信号分别送入对象级CNN和部分级CNN用于提取ECG信号不同粒度的特征，最终，将对象级CNN和部分级CNN所提取的形态特征融合提供给多层感知器进行QRS波群检测，准确率为99.67%。上述算法需对信号进行多次预处理操作，相当于对信号做滤波处理，会滤掉ECG信号中的有用信息且增加算法的计算复杂度。

本文提出一种基于1-D CNN的QRS波群检测算法，其不需要大量数据预处理，采用不同于前人的数据集制作方式，仅使用一个1-D CNN模型和非极大值抑制算法相结合就可以完成QRS波群的特征提取和检测。

1 方 法

算法框架如图1所示，主要分为数据预处理、1-D CNN模型和非极大值抑制算法3个部分。对数据进行重采样后，通过固定窗对数据进行截取和归一化形成心电信号片段喂入1-D CNN模型，最后通过非极大值抑制算法对1-D CNN输出的QRS波群检测概率序列进行处理，得到算法最终的QRS波群检测结果。

图1 基于1-D CNN的QRS波群检测算法框架

1.1 数据预处理

一个完整的心动周期在ECG中表现为一个完整的心拍，如图2所示，包括了P波、QRS波群和T波等，各个波形的不同形式往往体现了某些病变。在ECG的所有波形中，QRS波群最为明显，一般以它为基准来定位其它波的位置[3]。QRS波群检测是ECG信号分析诊断的前提和基础，只有QRS波群标定后，才有可能计算心率，检测ST段参数，区分正常和异常心拍，进而对心律异常进行分析。

图2 心拍波形

心电信号的频率分布在0.05 Hz-60 Hz之间，而信号中常见的干扰，如基线漂移、工频干扰和肌电干扰分布在信号的不同频段，任何去噪都会滤掉信号中的有用信息。因此，本文不对数据做去噪处理。

采样频率的高低对心电信号的波形产生很大的影响，提高采样频率能提高心电信号波形的质量，减少QRS波形的失真。当采样频率高到一定的数值之后，再提高采样频率对改善心电波形的作用就不明显了。为此，指定一个合适的采样频率是必要的。目前多数设备的采样频率为 125 Hz 左右，但是对于上限频率达到100 Hz的系统来说，合适的采样频率应该达到250 Hz，且为了使本算法能够更好的为可穿戴心电检测设备所使用，本文将所有数据重采样为250 Hz。

为了能够加快算法的收敛速度，方便后期数据处理，以QRS波群中的R波峰和随机非R波峰位置为中心，使用固定窗对数据进行截取形成心电信号片段后进行归一化处理。

1.2 1-D CNN模型

常见的二维卷积神经网络常被用来做图像分类，本文要处理的心电信号为一维离散序列，故先将二维卷积神经网络修改为适合于心电信号特征提取的一维卷积神经网络[4]。本文所使用的一维卷积神经网络结构如图3所示。

图3 1-D CNN模型结构

其由一个输入层，5个卷积层，4个池化层，5个归一化层，一个全连接层和一个输出层组成。前4个卷积层后面都尾随一个池化层和归一化层，第5个卷积层后面直接跟一个归一化层。

卷积层在上层的特征向量和当前层的卷积核之间执行卷积运算，使用Relu作为激活函数，可增强原始信号的特征并减少噪声，卷积层参数包括卷积核长度、滑动步长和填充，三者共同决定了卷积层输出特征向量的长度。其中卷积核长度可以指定为小于输入特征向量的任意值，卷积核越大，可提取的特征越复杂。滑动步长是卷积核在特征向量水平方向上每次的滑动长度，例如，若滑动步长为2时，卷积核隔一个点移动一次。随着卷积层的堆叠，特征向量的长度会逐渐减小。为此，填充的目的是人为增加特征向量的长度以抵消在计算中特征向量长度的减小，常见的填充方法为Same和Valid，本文所使用的填充方式为Valid，为非填充，P为0。每个卷积层后输出特征向量的长度X的计算公式为

(1)

式中：W为输入数据长度，F为卷积核长度，P的值要根据全0填充的类型来确定，S为卷积核滑动步长。

池化也称为下采样，其不会改变输入特征向量的个数，只会改变每个特征向量的长度，主要为了降低模型复杂度和减小过拟合。池化最常用的有最大池化和平均池化，本文采用最大池化来减小ECG数据的维数，对特征进行压缩，并提取有效特征。在池化核覆盖的特征向量区域内，选取最大值来替代当前区域的所有值[5]。每个池化层后输出特征向量的长度Y的计算公式为

(2)

式中：W为输入数据长度，F为池化核长度，S为池化核滑动步长。最终将全连接层的输出经过softmax得到概率值以计算分类结果。

1.3 非极大值抑制算法

本文数据集中以R波峰位置为中心的数据为正样本，任何以非R波峰位置为中心的数据都是负样本，卷积神经网络最终输出的是对一个样本判断的概率值，样本中心点越是靠近R波峰，概率值就越大，因此，1-D CNN模型在1个QRS波群上会有2-5个较大的概率值输出，如图4(b)为包含700个采样点的心电信号图4(a)对应的1-D CNN模型的概率输出。针对此问题，本文采用非极大值抑制的方法，若概率值大于1-D CNN模型分类的阈值，则使用包含10个概率序列的固定窗切割概率序列，若切割以后的概率序列中间值为最大，则此处为R波峰，如图4(c)所示。

图4 非极大值抑制算法的数据处理

2 实验及结果分析

首先，通过采用不同长度固定窗对心电数据进行切割得到3个不同长度的数据集，然后，通过将3个不同长度的数据集分别与两种归一化方式组合构成6组数据集后，将数据喂入1-D CNN模型得到6组对比实验结果，最后，通过将最优的1-D CNN模型和非极大值抑制算法相结合与传统QRS波群检测算法在测试集上作对比，得出本算法在准确度和抗干扰能力等方面都要优于传统的QRS波群检测算法。

2.1 数据切割与归一化方式

QRS波群最多可展宽至0.2 s，将数据重采样为 250 Hz 后，一个QRS波群可包含50个采样点，依据心电信号特性[6]，本文以MIT-BIH心律失常数据库提供的R波峰和随机非R波峰位置为中心左右分别各取50、75、100个采样点构成包含101、151、201个采样点的数据集，正、负样本数据分割如图5(a)，图5(b)所示。

图5 数据分割

MIT-BIH自带归一化方式如式(3)所示[7]，在将数据平移至中心点后进行伸缩处理。正常的RR间期在0.6 s-1 s之间[14]，所有非R波峰位置都作为负样本中心点的候选，因此，负样本中会有数据全取自上一心拍的S波与下一心拍的Q波之间，幅度较低，如图5(b)所示。将图5(b)中包含151个采样点的负样本数据单独取出，采用MIT-BIH自带归一化方式对数据进行归一化后，相当于对数据做平移拉伸，会导致其与QRS波群相似，如图6所示。针对此问题，本文对MIT-BIH自带归一化方式进行优化，对于最大值减最小值低于0.3 mv的数据仅对其进行平移不做拉伸处理

(3)

式中：x为当前ECG信号的电压值，xmax为该样本数据中最大值，xmin为该样本数据中最小值。

图6 归一化与未归一化数据

2.2 数据集

本文使用的ECG信号来自MIT-BIH心律失常数据库和中国科学院计算技术研究所天津分所大象随心宝可穿戴设备采集的数据。将MIT-BIH心律失常数据库的数据分为训练集和验证集，以验证本方法的可行性；将可穿戴设备采集的数据作为测试集，以检验算法的准确度、鲁棒性及抗噪声能力。

MIT-BIH心律失常数据库包括48个双通道动态心电图记录，前23个记录是从常规门诊患者的数据中提取的，而剩下的25个记录是由于包含一些比较少见、复杂且不易识别的室性、交界性、室上性心律失常以及传导异常等临床常见异常而选择的，其48个双通道信号分布见表1。正常QRS波群通常在第一个通道特征显著，第二个通道信号导联轴差不多与平均心电轴正交，为了准确定位QRS波群位置，本文采用的是第一通道信号。在MIT-BIH心律失常数据库中选择46条记录(102和104记录两通道信号均不来自MLII导联，本文不将其作为数据集)按照跨病人的方式分为训练集DS1和验证集DS2，其中DS1=(101，106，108，109，112，114，115，116，118，119，122，124，201，203，205，207，208，209，215，220，223，230)，DS2为剩下的24条记录[8]。

表1 MIT-BIH心律失常数据库每条记录的通道分布

通过对DS1和DS2中的记录做分割和归一化处理，最终3个不同长度数据集中训练集与验证集所含数据量见表2。

表2 数据集

用户通过将可穿戴设备粘贴于胸部，如图7(a)，图7(b)所示，获得250 Hz采样频率的模拟导联心电数据。本文在大象随心宝可穿戴设备所有用户中随机抽取50条较为常规的心电数据，记为first_50，然后随机抽取50条混有心肌缺血、基线漂移、工频干扰的心电数据，记为last_50，每条数据时长为10 min。

图7 可穿戴设备数据采集

为了检测算法的实时效果，针对测试集，本文不对其进行整体数据切割，而是通过每次滑动一个采样点的方式滑动固定窗对数据截取和归一化后直接喂入1-D CNN模型，经过非极大值抑制算法，输出连续的概率分布，来实时展示本算法的QRS波群检测效果。

2.3 评价指标

用于评估检测性能的测量指标是假阴性率(false negative rate，FNR)，假阳性率(false positive rate，FPR)和准确率(accuracy，Acc)，它们分别通过式(4)～式(6) 计算

(4)

(5)

(6)

其中，TP为正样本预测为正样本的数量，FP为负样本预测为正样本的数量，TN为负样本预测为负样本的概率，FN为正样本预测为负样本的数量。

2.4 1-D CNN模型特征提取

1-D CNN模型在对数据进行分类时，只需我们将数据输入网络，在模型内部通过前向传播和反向传播算法不断更新参数找到全局最优解或局部最优解来自动进行特征提取，在每个卷积层所提取的特征中随机选取3个并进行可视化，如图8所示，其中第一排为原始数据，后面依次是1-5卷积层随机选取的3个特征向量。

图8 特征向量可视化

从不同卷积层可视化出来的特征向量图可以得出：①浅层网络提取的是纹理，细节特征；②深层网络提取的是高纬度特征，可视化后的特征图越来越抽象，可解释性差，这也是卷积神经网络所存在的一个缺陷。

2.5 1-D CNN模型实验结果

实验结果见表3，可以看出，采用相同的归一化方式，包含101个采样点的数据集所训练的模型假阴性率过高，包含201个采样点的数据集所训练的模型假阳性率过高；相同数据集长度条件下，采用优化归一化方式所训练的模型在3个评价指标上都要优于MIT-BIH自带归一化方式所训练的模型，且在假阳性率和准确度上提升较为明显。由此可见，151个采样点与优化后的归一化方式组合，算法效果最佳。

2.6 最优检测算法实验结果

将该算法、苏志同等[9]提出的差分阈值算法以及 Merah 等[10]提出的小波变换算法均应用于测试集实时进行QRS波群检测，最终在100条测试集数据的准确度上求统计平均，1-D CNN检测算法准确度为98.51%，小波变换算法准确度为95.75%，差分阈值算法准确度为92.34%，本文算法要明显高于其它两个传统算法。在first_50和 last_50 数据上面的表现性能如图9所示，传统算法和本文算法对于常规的心电信号准确度相差无几，差分阈值方法仅有一条数据较低，但准确度也高于95%，然而，在混有基线漂移、工频干扰、肌电干扰等干扰的数据中准确度差别较大，充分说明本算法在抗干扰方面明显优于现有的QRS波群检测算法。

心房颤动(atrial fibrillation，AF)简称房颤，是一种常见的心律失常。发生房颤时心电图表现为：①P波消失，出现一系列连续并且不规则的心房激动波，称为f波；②RR间期绝对不规则[11]，房颤波形如图10心电信号所示。在心电信号幅值较低的患者中会将f波误判为R波，进而对心律失常进行误判，影响患者治疗。本算法在房颤心电信号的表现性能如图10中检测结果所示，能够很好的对房颤患者的心电信号进行准确的QRS波群检测。

表3 实验结果

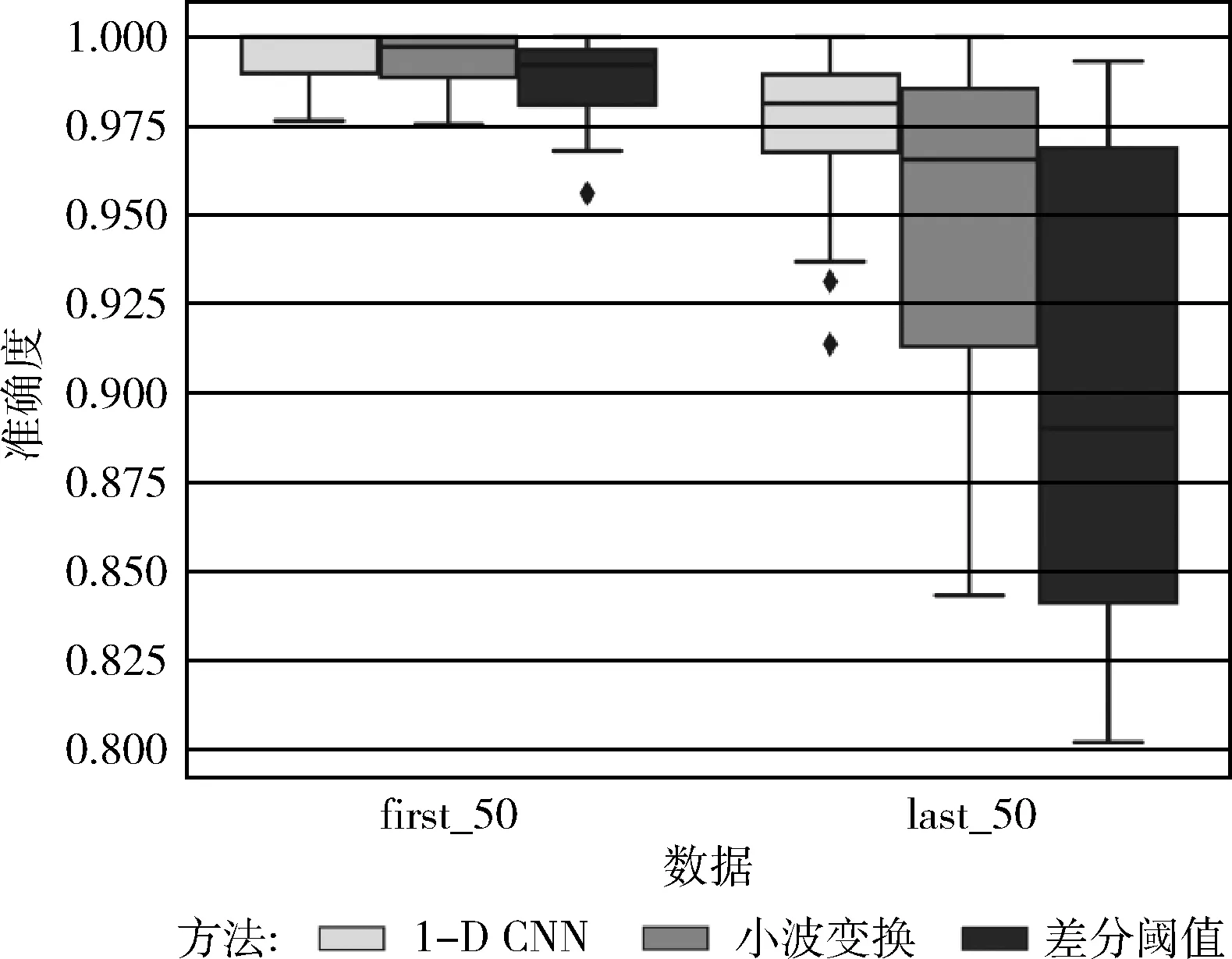
图9 实验结果对比

图10 房颤心电数据

在ECG的采集过程中，由于电极与体表接触不良、电极电阻变化、人体呼吸或其它肌肉缓慢运动等，导致ECG发生基线漂移，如图11中心电信号所示。在大多数研究中，都会通过曲线拟合、小波变换或自适应滤波等方法来消除基线漂移对心电信号的影响[12]，本文算法在不去除基线漂移的前提下，能够很好地识别混有基线漂移的心电信号中的QRS波群，如图11中检测结果所示。

图11 基线漂移心电数据

在心电图的采集、转化过程中容易受到环境和设备的影响，产生噪声，特别是50 Hz的工频干扰[13]。相比于在医院检查时静息状态下采集的心电信号，动态心电图是在人们运动中采集的，其中会混有大量的工频干扰，如图12中心电信号所示。因此，准确定位混有工频干扰的心电信号中QRS波群的位置，为患者的诊断提供良好的基础是至关重要，本算法在混有工频干扰的心电信号中的QRS波群检测的表现性能如图12中检测结果所示。

图12 工频干扰心电数据

3 结束语

本文通过将不同数据集长度、不同归一化方式组合作对比实验，得出结论：①在250 Hz采样频率下，对比3个不同长度数据集所训练模型的实验结果，取151个采样点所训练模型的QRS波群检测效果最好，101个采样点数会导致QRS波群检测假阴性率增高，201个采样点数会导致QRS波群检测假阳性率增高；②本文通过优化归一化方式试图解决非QRS波群因幅度较低经原始归一化后被判断为QRS波群的问题，实验结果表明新的归一化方式在假阳性率和准确度上都有所提升；③为了避免心电信号中的有用信息被过滤掉，本算法在不对数据做去噪处理的情况下，具有较好的噪声鲁棒性。

实际生活中，动态心电数据会因个体、时间、环境等因素发生变化，仅使用MIT-BIH心律失常数据库来对模型进行训练，不足以满足患者心电数据的特异性，还需要更多的数据加入模型训练来提高模型的鲁棒性；此外，QRS波群检测几乎是所有ECG自动分析的切入点，仅对其研究是不够的，接下来还需要对单个心搏进行分类，进而利用医学知识，根据心搏的排列顺序以及心率来对心律失常进行判断，以此来减少医生工作量，提高医生的工作效率。