基于改进粒子群优化的移动云应用卸载决策

李廷元

(中国民用航空飞行学院 计算机学院，四川 广汉 618307)

0 引 言

移动互联网的兴起，使得人们在移动终端上执行任务的需求越来越普遍，所执行的任务类型也越来越多样和复杂[1]。这类应用任务由大量非计算密集型任务和计算密集型任务构成。尽管元器件技术的更新换代使得移动终端的处理能力大幅提高，但是对于处理计算密集型任务仍然存在瓶颈问题[2,3]。通过云计算技术，移动终端可以将自身任务提交至远程无端执行，即移动云计算技术[4,5]。移动云计算环境下，应用任务从本地移动终端提交至功能更强大的云端资源执行，即为任务卸载技术[6-8]。由于任务卸载同时受到网络传输带宽资源及云端资源能力可用性的影响，任务卸载是否可以减小任务执行延时需要综合考虑。目前多数研究侧重于研究如何卸载部分任务至远程云端，以提升终端能效[9,10]。

目前的移动云环境中的任务卸载多集中于单站点环境[11,12]。然而，多站点环境下的任务卸载比单站点环境将拥有更好的性能表现。问题在于，多站点任务卸载求解是NP难问题。针对该问题，提出一种基于权重代价模型的多服务选择任务卸载决策算法。算法以权重代价模型综合考虑任务的执行时间和能耗，然后利用粒子群优化算法对任务卸载进行求解。同时，算法在粒子群优化过程上做了一些改进，包括通过预定义粒子种群提升种群丰富性，通过改进初始化操作和粒子进化操作提高了得到最优任务卸载决策的概率。

1 相关研究

文献[13]利用整数线性规划对任务卸载问题进行了求解，但仅仅优化了能耗。文献[14]同样考虑了能耗目标，提出一种基于资源按需分配的任务卸载算法。文献[11]引入网络带宽资源至任务卸载决策中，可以在执行效率和能耗间进行多目标优化。文献[12]通过遗传算法对工作流任务的卸载决策问题进行了求解，其适应度函数中综合融入了执行时间和执行能耗，可以优化综合代价。文献[15]提出一种任务卸载决策方法，在满足执行期限的同时对执行能耗进行了优化，可以实现任务分割的最优解。文献[16]在随机无线信道中以路径约束为基础设计了一种自适应任务卸载算法，进一步降低了能耗。文献[17]综合考虑能耗、延迟、子任务执行依赖，提出了联合卸载算法。以上研究方法均是基于单站点环境的任务卸载决策问题，无法应用于多供应方的云服务环境。

文献[18]利用粒子群优化算法设计了多站点环境下的任务卸载策略，虽然综合考虑了网络带宽和能耗问题，但算法复杂性较高，可能导致进行任务卸载决策的时间高于在本地终端上进行任务执行的时间。文献[19]提出一种基于蚂蚁优化算法的卸载决策算法，算法将收益和风险综合考虑至卸载决策中，具有较好的可行性。然而，以上多站点环境下的任务卸载虽然有一定可行性，但是忽略了影响任务卸载决策的一些重要因素，如：在执行延时、执行能耗或网络传输带宽无法综合考虑，而利用元启发式方法得到的卸载决策复杂度过高等问题。基于此考虑，本文综合考虑执行时间和本地设备的执行能耗，通过改进的粒子进化操作，对多重服务提供与选择的任务卸载问题进行求解，并通过仿真实验与同类算法的对比，验证算法的可行性和有效性。

2 模 型

表1给出本文相关符号说明。

2.1 任务构成

表1 符号定义及其说明

2.2 面向多站点的计算卸载模型

本节将面向多站点的计算卸载模型形式为一个考虑应用总体执行时间与总体执行能耗的权重代价模型。

(1)权重代价模型

将多站点计算卸载问题描述如下：寻找最优分割X’，满足X’=argmin(W(X))。 当分割解为X时，权重代价W(X) 为

(1)

(2)

其中，Θ(X)为执行时间，Φ(X)为执行能耗，ΘLocal为本地执行时间，ΦLocal为本地执行能耗，时间权重wθ和能耗权重wφ用于决定用户偏好，wθ=1且wφ=0为时间优化模型，wθ=0且wφ=1为能耗优化模型。

(2)时间模型

对于计算卸载决策解，执行时间由所有任务单元在本地或云站点上的执行时间与通信时间组成，任务执行时间为节点权重。时间优化模型目标是：寻找最优分割X’，满足X’=argmin(T(X))。 分割解X下执行时间Θ(X)计算为

(3)

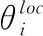
(4)

(5)

(6)

任务在本地执行的时间由式(7)计算，在远程云端执行的时间由式(8)计算

(7)

(8)

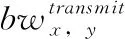
(9)

(3)能耗模型

执行能耗由任务执行能耗和通信能耗组成。能耗优化的目标是寻找最优分割X’，满足X’=argmin(Φ(X))。 分割解X下的执行能耗Φ(X)为

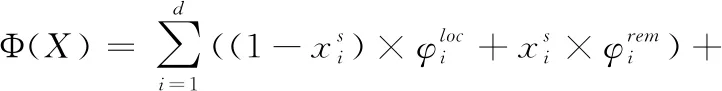
(10)

约束条件为

(11)

(12)

(13)

(14)

(15)

其中，pCPU为移动设备CPU的功率，ptransfer为传输功率。

3 OMPSO算法设计

本文设计一种基于粒子群优化的多站点计算卸载决策算法OMPSO，问题的解抽象为侯选粒子的集合，即粒子群。OMPSO算法中，每个粒子代表应用的一个分割解X，粒子由应用任务单元组成，即维度。粒子的每个维度附有一个值，代表分配给该任务的执行站点，图1代表一个算法中的粒子，OMPSO算法以最小化权重代价为目标，得到最优分割X’。执行步骤如下：

算法1： OMPSO

(1) Population Initialization

(2)Repeat

(3) Position Update//粒子位置更新

(4) Global_best Update//全局最优解更新

(5)Untilthe stop criteria are reached//判定迭代结束条件

图1 OMPSO算法中的粒子结构

3.1 种群初始化

该步骤初始化算法参数，包括：最大迭代次数I，粒子群模型SS，以及粒子本身也需要初始化。除了PSO中利用初始粒子群OS之外，算法还引入预留粒子群RS丰富OMPSO算法中的粒子。RS中的粒子(为任务分配的执行站点)与OS具有很大不同，可获得更高的适应度，这有助于丰富OMPSO中的粒子多样性并降低搜索过程陷入局部最优解。此外，多数遗传和粒子群进化操作以随机方式进行种群初始化，OMPSO算法将联立预定义和随机粒子的方式对粒子群进行初始化。根据移动云的卸载目标，由于任务卸载优于本地执行，算法先创建一个粒子，其所有任务单元均分配至本地执行，这有助于在迭代中保护更有效的粒子(其执行代价低于本地执行代价)。另外，根据云端服务器的数量M，进行粒子初始化，其所有粒子均分配至一个云端服务器，生成M个粒子。剩余粒子则随机产生。然后，为了获得每个粒子群中的最优粒子，以适应度对粒子排序，最优个体被选择为粒子群的全局最优粒子。算法2为初始化过程。

算法2： Initialization-初始化

(1)setOSas original swarm,RSas reserve swarm

(2)set maximum iteration numberI,swarm sizeSS, application unit numberdand execution sitesS

(3)fori=1 toSdo

(4)forj=1 toddo

(5) OS[i][j]=i-1

(6)RS[i][j]=random[0,S-1]

(7)endfor

(8)endfor

(9)fori=S+1 toSSdo

(10)forj=1 toddo

(11)OS[i][j]=random[0,S-1]

(12)RS[i][j]=random[0,S-1]

(13)endfor

(14)endfor

(15)fori=1 toSSdo

(16)OS_fitness[i]=set fitness by Equ.1//计算初始粒子群适应度

(17)RS_fitness[i]=set fitness by Equ.16//计算预留粒子群适应度

(18)endfor

(19)Ascending SortOS_fitness//初始粒子群作适应度降序排列

(20)Ascending SortRS_fitness//预留粒子群作适应度降序排列

(21)global_bestOS=the best particle ofOS_fitness//选择初始粒子群的最优粒子

(22)global_bestRS=the best particle ofRS_fitness//选择预留粒子群的最优粒子

3.2 适应度函数

OMPSO算法中，初始粒子群的适应度函数定义为式(1)。由于使用了预留粒子群丰富粒子多样性，基于预留粒子群的目标设计另一适应度函数，RS的适应度函数定义为

(16)

其中，SS表示粒子群规模，Pi表示OS中的第i个粒子，Pr表示RS中的给定粒子，H表示汉明距离函数，定义为

(17)

其中

(18)

FRS(r) 的汉明距离函数用于根据任务分配站点的不同计算给定粒子间的差异，gi,k表示初始种群中的粒子i的维度k，gr,k表示预留粒子群中的粒子r的维度k。

3.3 粒子更新

该步骤以维持在速度上的概率改变维度的分配站点(位置)至新站点，从而使粒子收敛至更优解上。速度上保存概率是为了改变每个维度的分配站点到特定站点序号上。如图2是OMPSO算法的速度表示。为了指定维度的值，需要从粒子群选择3个最优粒子。然后，每个粒子的对应维度根据OS和RS的局部适应度进行比较，两种适应度分别定义为

(19)

(20)

(21)

(22)

(23)

(24)

每个粒子群中的粒子或者根据对应速度的概率改变其位置至速度的分配站点，或者保持在当前位置上。

图2 OMPSO算法中粒子的速度表示

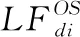
图3 OMPSO算法的杂交繁育实例

算法3： Position Update-粒子位置更新

(1)fori=1 to 3do

(2)forj=1 toddo

(5)endfor

(6)endfor

(7)fori=1 to 3do

(8)forj=1 toddo

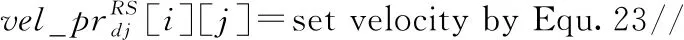
(11)endfor

(12)endfor

(13)fori=1 toSSdo

(14)OS[i]=update position byvel_prOS//更新初始粒子群粒子位置

(15)RS[i]= update position byvel_prRS//更新预留粒子群粒子位置

(16)endfor

(17)OS=crossbreeding(POSbest,PRSbest)//初始粒子群的杂交繁育

(18)RS=crossbreeding(POSbest,PRSbest) //预留粒子群的杂交繁育

(19)foritoSSdo

(20)OS_fitness[i]=set fitness by Equ.1//计算初始粒子群的适应度

(21)RS_fitness[i]=set fitness by Equ.16//计算预留粒子群的适应度

(22)endfor

(23)OS=keep the bestOSparticles//初始粒子群更新

(24)RS=keep the bestRSparticles//预留粒子群更新

3.4 全局最优更新

该步骤中，当前迭代中每个粒子群中获得的最优粒子与粒子群的全局最优global_best粒子比较，若当前迭代中的最优粒子优于全局最优粒子，则更新全局适应度。当到达预先定义的迭代次数或结果无法进一步更新时，OMPSO算法停止执行。OS中获得的全局最优粒子选择为多站点计算卸载问题的最优分割解X’。

4 实验评估

本节评估OMPSO算法的性能，以下将分别描述在仿真实验和试验台实验中的参数取值。实验中，式(2)中的时间因子和能耗因子均等于0.5，即应用执行对于执行时间和执行能耗具有同等的偏好，该取值可根据用户应用的执行需求进行调整。

4.1 仿真实验环境配置

仿真实验中，所有算法在配置为2.3GHz Intel core i7CPU和8 GB RAM的计算机上以JAVA实现。实验分别利用从现实应用抽象出的任务图和随机任务图进行仿真测试。为了评估应用规模的影响，实验生成了拥有不同数量顶点和边的不同随机图。对于现实应用的任务图，3种SpecJvm基准统计的开源应用DB、JESS和RayTrace通过统计分析用于现实应用测试。表2和表3给出了随机任务图和现实任务图的特征描述。假设现有4个执行站点可用，包括一个本地站点和3个过程云服务器站点。网络带宽范围为10 Kbytes/s～100 Kbytes/s，本地移动设备的CPU功率和数据传输功率与具体利用硬件相关，本文利用华为P6的硬件配置。

表2 随机应用任务图特征

表3 现实应用任务图特征

4.2 参数影响

OMPSO算法的执行首先需要获得最适合的参数配置，本节将通过实验获取算法得到最优结果时粒子群规模SS和最大迭代次数I，具体实验场景见表4。

图4和图5描述了两个参数对OMPSO的影响。图4代表场景C1下粒子群规模SS对算法的影响，同时考虑了DB和RayTrace应用。可以看到，粒子群规模的增加对OMPSO有直接影响，且在SS=50时算法得到了最优的适应度，大于50后，权重代价无明显改进，故设置SS=50作为OMPSO算法的最优粒子群规模。图5代表场景C2下迭代次数I对算法的影响。随着迭代次数的增加，在I=30时，算法得到了最优适应度，继续迭代并未对结果产生明显影响。故设I=30作为OMPSO算法的最优迭代次数。

表4 参数配置

图4 粒子群规模对权重代价的影响

图5 迭代次数对权重代价的影响

4.3 性能仿真对比研究

本节做算法的对比分析，实验参数设置如4.2节所述，对比算法包括：

(1)本地执行算法Local：该算法中所有应用任务均执行于本地移动设备上，该算法可用于衡量其它算法得到的卸载增益；

(2)标准粒子群算法SPSO：该算法即为常规的PSO算法；

(3)MMRO算法[19]：该算法利用蚁群算法实现多站点任务卸载决策。

表5给出了算法做出卸载决策的时间，可以看到，算法卸载决策时间是相近的，但OMPSO的时间略长于MMRO和SPSO，这是由于算法计算卸载最优解的粒子进化步骤有所改进导致的，但算法复杂度并未增加。

表5 算法卸载决策时间

图6～图8是迭代次数对任务总体执行时间(图6)、执行能耗(图7)和权重代价(图8)的影响。实验中传输带宽设置为100 Kbytes/s，粒子群规模为50。图中结果表明，Local算法由于在本地执行所有任务，执行时间不会发生变化，因为本地处理能力是固定的。由于本地处理能力远小于云服务站点的处理能力，故Local算法在各项指标上均是最差的。OMPSO算法相比其它算法可以更少的迭代次数得到更优解，表现在任务执行时间、执行能耗和权重代价均是最小的。与SPSO相比，OMPSO在初始化过程中引入预定义粒子群，使得初始粒子群中的粒子更加丰富且初始适应度更高，有利于后继进化时的最优解生成。而粒子更新中为不同类型粒子群定义不同适应度的方法也可以进一步使粒子进化加速收敛，也利于最优解生成。而MMRO算法虽然利用蚁群优化的思想可以降低应用执行代价，但没有根本解决局部收敛的问题，使得最终解并非真正的最优解。

图6 迭代次数对执行时间的影响

图7 迭代次数对执行能耗的影响

图8 迭代次数对权重代价的影响

图9～图11是传输带宽对任务总体执行时间、执行能耗和权重代价的影响。显然，增加带宽会降低执行时间，原因在于增加带宽虽然未影响任务在站点上的执行时间，但会降低数据的传输时间。OMPSO算法通过本文设计的粒子群进化机制更好生成了应用分割与卸载解，且在传输带宽较低时，性能也未受到明显影响。对比算法的性能结果在较低带宽时甚至得到了比本地执行更高的代价，这说明SPSO和MMRO算法仅在卸载环境拥有较高带宽时才可能通过任务分割与卸载产生更小的权重代价，对带宽的依赖性远高于本文算法。综合来看，OMPSO算法不仅在3个性能指标表现更高，并且对环境参数的改变具有更好的适应性。

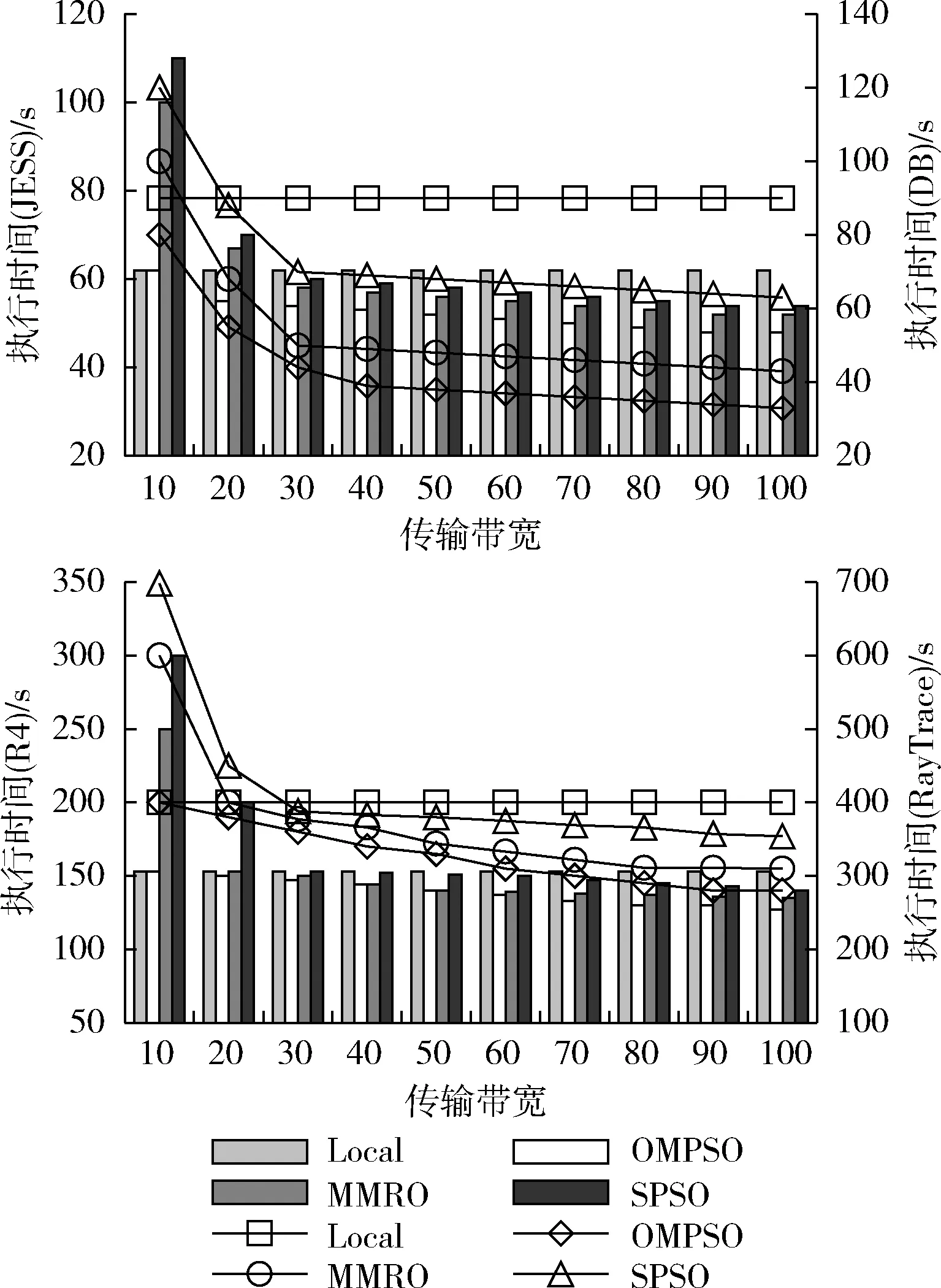
图9 传输带宽对执行时间的影响

图10 传输带宽对执行能耗的影响

图11 传输带宽对权重代价的影响

4.4 实验床对比研究

现实实验床研究中，选取Huawei V9和Galaxy S6两款智能手机作为移动设备，选择3台不同计算能力的计算机作为异构的远程卸载服务器，配置8 G RAM，CPU配置分别为2.3 GHz core I7、1.6 GHz core I7和2.2 GHz core I5。作为执行的移动样本应用，选择斐波那契算法、N-皇后求解和子串搜索求解3个问题运行于Android平台上，以上3个问题在相应输入规模n较大时，其执行时间也较长。分别利用在手机Android平台上的本地执行方法和本文提出的OMPSO算法在不同的输入值n下对以上问题进行求解。表6～表8的结果表明，CMPSO算法在执行3种应用时得到的执行时间优于本地执行算法。此外，算法得到的执行时间均随着n值的增加而增加，而本地设备在求解规模较大甚至无法求解出3个应用任务的解，这源于其本地设备RAM受限，执行时间过长，此时以N表示。综合来看，CMPSO算法可以比本地执行更快获得求解问题的解，验证算法是有效可行的。

表6 斐波那契算法执行时间/s

表7 N-皇后求解执行时间/s

表8 子串搜索求解执行时间/s

5 结束语

为了优化移动云计算中应用执行延时和移动设备能效，提出基于粒子群优化的移动云应用卸载决策算法。算法利用了预定义和随机粒子群方法混合生成粒子群的初始种群；为预定义的预留粒子群设计一种基于汉明距离函数的适应度函数，更好衡量粒子差异；为丰富种群多样性，利用杂交繁育生成了变异粒子。改进粒子进化操作可以更合理地获取应用分割的最优解。仿真结果表明，改进算法在能耗、效率及综合权重代价指标上均表现更好。