混沌BA的电机网络控制系统安全诊断策略

刘嘎琼，卢道华，田宝强，刘 镇

(1.江苏科技大学 计算机科学与工程学院，江苏 镇江 212003；2.江苏科技大学 海洋装备研究院，江苏 镇江 212003)

0 引 言

工业控制系统[1,2]中传感器与执行机构分布广，且工作条件恶劣，易发生故障。工业控制电机网络控制系统网络控制系统与传统数字控制系统相比最大的不同在于其相关数据是通过总线进行传输，但是也正是由于总线的存在导致其诱导时延以及数据丢包等问题，使得在进行故障诊断时必须将总线带来的不利因素考虑进去。王越男为离散时间延迟系统设计了功能强大的故障检测观测器，有效实现了对故障的鲁棒检测要求[4]。文献[5,6]则针对时滞系统实现了H∞故障检测，结果表明了上述方法在故障检测领域的有效性。虽然上述方法均能够一定程度的实现故障检测，但是都是以抑制噪声为出发点，极大地限制了故障检测准确率的提升。

为同时提升检测系统对噪声信号的鲁棒性以及故障信号的敏感性，提出基于混沌变异蝙蝠优化算法的安全诊断优化设计方法。

1 系统建模

根据文献[3]可知存在如下假设：①传感器、控制器、执行器均为事件驱动，周期为T。②忽略计算时间带来的延迟。③系统通过静态调度实现。④忽略数据包丢和数据包错乱。

工业电机网络控制系统可以将其看作一个整体进行建模[2]，具体的离散时间模型

(1)

B1，Β2，E，H1，H2代表的是常数矩阵，F(τk)表示的是关于τk的时变矩阵，且存在如下关系式：F(τk)TF(τk)≤I[7]。其中，ΔB1=EF(τk)H1，ΔB2=EF(τk)H2。

进一步建立观测器误差模型。传感器将数据发送给控制器的每个控制状态量封装在多个数据包中,并且将从每个控制器发送数据给执行器的每个控制状态量封装在不同数据包中,因此每个控制器和系统通过执行指令的机制接收传感器执行指令的状态量x(k)与执行器的控制量u′(k)分别为x′(k)与u(k)。

静态调度的应用可以使多数据包传输转换为具有两个交换机的交换系统。当在k时刻，开关K1和Si(i=1,2,…,m)连接，而开关K2则和S′j(j=1,2,…,n)连接，此时，未发送的数据分组被认为是分组丢失，令k-1时刻的数据替代。当前正在发送传输状态和控制变量，并且此时的数据变为当时的状态。因此，存在如下关系

(2)

故

(3)

同理，控制量的各个数据包之间有如下关系

(4)

即

(5)

状态反馈如下所示

(6)

(7)

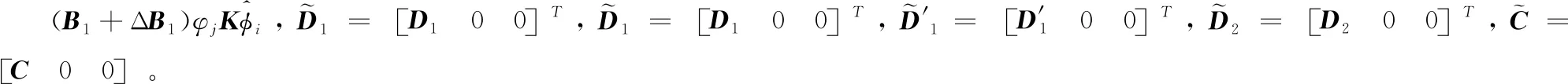
2 改进BA算法

蝙蝠算法一经提出，就由于其简单性与有效性得到了广泛的关注[8-10]。

具体的蝙蝠算法迭代过程为：蝙蝠的坐标为一个解，该坐标包含了速度和适应度函数值，蝙蝠种群利用新发出的频率、脉冲发射速率和声波响度得到新的解集，然后一次进行迭代得到最优值[11,12]。迭代过程的数学表达式如下

Fi=Fmin+(Fmax-Fmin)×RN,RN∈[0,1]

(8)

(9)

(10)

为提升算法的便利性，给出相应的更新公式如下

Xnew=Xbest+α×Al

(11)

其中，α代表在[-1,1]区间内的随机数；Al表示为第l代蝙蝠声波响度的平均值。

在式(11)的基础上，每一只蝙蝠的脉冲发射率Ri以及相应的脉冲声波响度Ai也会进行更新，具体的更新过程如下所示

(12)

(13)

式中：β，ω代表常值，β>0，0<ω<1。

BA具有收敛性强以及搜索范围大的优点，但是蝙蝠位置的更新效果过分依靠速度参数，使得在优化过程后期，容易陷入局部极值[13,14]。为提升其优化精度，将遗传算法中的理论与基本BA算法结合，具体步骤如下：

步骤1 将交叉比例和交叉方法引入蝙蝠种群的更新过程，具体的过程如式(14)所示

(14)

步骤2 为使得更新后的xi(t+1)发生变异，设置相应的变异激活函数如式(15)

(15)

其中，α∈[0.5,0.6]，β∈[0.1,0.3]，k代表种群内第k只蝙蝠，n代表维度，N代表蝙蝠种群的总个数，rand是[0,1]的随机数，若满足Activate(k)<1，则使得蝙蝠发生变异；

步骤3 变异主要包括均匀变换以及高斯变换，均匀变换主要为了提升收敛速度，高斯变换主要提升跳出局部极值的能力，相应的均匀变换和高斯变换如下式所示

(16)

其中，σ代表高斯分布的标准差。

在BA中，已知脉冲发射率更新迭代的初始值选则具有一定的主观性，因此该参数选择可能是的算法具有一定的人为保守性而无法达到最优。因此进一步改进脉冲发射率的迭代过程

(17)

图1 混沌BA脉冲发射率

图2 基本BA脉冲发射率

3 改进BA的故障检测观测器设计

设闭环观测器为

(18)

式中：Ll(l=1,2,…,m×n)表示的是目标增益矩阵，其系统结构如图3所示。

图3 观测器结构

(19)

通过等式(19)的Z变换能够将上式转换为传递函数矩阵

(20)

其中，Gf代表的是残差ε与故障f的传递函数矩阵，Gω表示的是残差ε与干扰ω的传递函数矩阵。

但是优化该增益矩阵必须首先满足如下几条原则：

(1)稳定性。

(2)灵敏性。

(3)鲁棒性。

根据文献[3]可知系统满足稳定性的充分条件如下

(21)

因为矩阵Ωij存在不确定矩阵F(τk)，所以进行如下变换

(22)

将式(22)代入式(21)中，根据文献[6]可知该式等价于：存在ηl>0(l=1,2,…,m×n)，使得

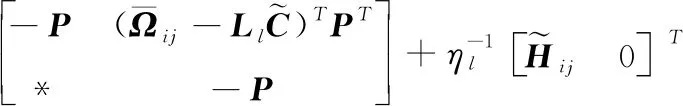
(23)

(24)

因此，稳定性充分条件可以转换为：增益矩阵Ll必须满足存在对称正定矩阵P以及ηl>0(l=1,2,…,m×n)，使得矩阵不等式(24)成立。

令优化问题的适应度函数如下所示

(25)

式中：J1表示的是系统与干扰信号之间的传递函数系数矩阵，ωr表示的是干扰信号的频率大小，J1应尽可能小，以减少干扰对系统的影响。J2表示的是系统对故障的传递函数系数矩阵，参考文献可知z=1。优化的目的是使拟合函数最小，从而使系统对故障信号更敏感，对干扰信号更具有鲁棒性。

因此优化问题可以转换为

(26)

具体的优化步骤为：

步骤1 设置算法的基本参数与初始值大小，给定输入为观测器矩阵的元素，并且计算出初始适应度函数值；

步骤2 对蝙蝠种群进行交叉运算，判断蝙蝠个体是否发生了变异，若发生变异，则按照变异过程进行处理；

步骤3 更新此时的蝙蝠种群位置，求解线性矩阵不等式(26)，如果求出可行解，则更新后的种群以细微扰动量在当前最优解附近重新寻优，否则重新进行位置寻找；

步骤4 计算蝙蝠种群新位置的适应度函数值，并更新声波响度、混沌脉冲发射率以及最优值；

步骤5 对比得到当前种群内适应度函数的最优值，并记录最优值的位置；

步骤6 判断是否达到最大迭代次数Iterate_times，若到达，则得到增益矩阵Ll；若未满足，返回步骤2。

4 实验与分析

4.1 仿真平台介绍

实验所用的半物理平台为分布式框架结构。图4显示了该平台的设计框架思路。该系统主要包括：仿真计算机和控制器、智能执行器和智能传感器以及CAN总线。仿真计算机实现发动机数学模型的仿真。智能传感器实现数据测量以及初步转换并将其通过CAN总线传至控制器。控制器实现相应的控制功能，并输出控制信号控制智能执行机构。智能执行器收到CAN总线的数据之后实现相应的控制行为。整个过程实现闭环控制。系统照片如图5所示。

图4 系统框架

图5 网络控制系统仿真平台实物

4.2 仿真分析

设工业电机网络控制系统表达式为

(27)

设置采样周期时间T=20 ms可得

(28)

(29)

首先进行参数的初始化设置，设置的根本依据是遵循试凑法的原则以及相关参考文献的结论而来[16]。令寻优解域属于[-10,10]6，令采样步长设置τ=20 ms，gmax=1000，sizepop=100，相关参数设置为m=5,α0=β0=0.7。

以基本蝙蝠算法以及改进蝙蝠优化算法对优化问题(26)进行迭代优化，相应的结果如图6和表1所示。

从图6和表1中可以看出,改进蝙蝠优化算法到达极小值时的收敛速度比基本BA快7个迭代周期。且改进蝙蝠优化算法收敛曲线无明显的转折,进一步表明该方法不易陷入局部最优，改进蝙蝠算法具有更好的优化效果。

图6 优化结果对比

表1 优化结果对比

从表1中可以得到最优适应度函数所对应的故障观测器矩阵为L1=[0.3552-0.99011.30210-0.57970]T，同理可得其它3种情况的观测器增益矩阵为

由于系统发送的数据量很少，因此数据包的数据量仅为在半物理平台上模拟双通道多数据包传输所需的3位。因此将第四个数据位设置为CAN总线数据包标识位。通过该标识位识别不同的数据包，图7显示了发送设置数据包的随机序列。

图7 数据包随机传输序列

传感器发生短路故障，则状态变量会出现一个突变，该种故障模式与阶跃型故障十分类似，故通过阶跃故障来模拟短路故障，对系统施加一个幅值较小的阶跃型故障，当添加了一幅度为0.92的干扰信号。检测结果如图8和图9所示，分别显示了经典检测方法以及改进蝙蝠优化算法优化检测方法的结果。经典方法的残差信号的抖动幅度为0.12，而优化方法的残差方法的振动幅度仅为0.069，表明添加的干扰对经典检测方法会产生显著的影响，使得设置阈值并不能完全区分状态。而提出的检测方法对故障信号实现了显著的放大,另外还大大降低了干扰信号幅值。提出的方法使得阈值设置范围从经典方法的0.12～0.166增加至0.069～0.202。该范围扩大了3.52倍，表明该方法有助于区分故障状态和正常状态。

图8 传统鲁棒观测器检测残差

图9 改进BA观测器检测残差

另外，传感器中若发生漂移故障，将会导致状态变量一某一斜率变化，该型故障与斜坡故障十分切合，故通过斜坡故障进行模拟。令传感器漂移模拟故障为f=0.15*(t-20)*δ(t-20)，图10显示了当添加一幅度为0.11的干扰时，使用经典方法和改进蝙蝠优化方法获得的残差的比较图。从图10中可以发现，经典方法针对干扰信号的十分敏感，相反，优化的故障观测器方法可以显著降低噪声含量,并且故障信号具有显着的放大效果,从而导致阈值和系统漂移的快速判别误差。

图10 斜坡故障监测残差对比

进一步给定一个传感器的非线性故障

(30)

添加一幅值为0.08的噪声信号。图11展示了检测残差的比较结果。经典方法的误差振动约为0.0042，而优化方法的误差振幅为0.0022。结果表明，噪声信号对传统的检测方法影响很大。此外，优化方法的阈值选择范围是0.0022～0.0184，而经典方法的阈值选择范围是0.0042～0.0083，相当于优化方法的阈值选择范围相比经典方法增大4.12倍。此外，验证了这种优化方法可以更好地辨别故障和正常情况。

图11 非线性故障检测残差对比

总之，改进蝙蝠算法优化的观测器增益矩阵可以将干扰信号放大，并减少干扰的影响。这样可以有效降低故障误诊率，提高故障检测的准确性。

5 结束语

针对工业电机网络控制系统，提出了基于混沌变异蝙蝠优化算法的安全诊断优化设计方法。通过仿真验证可得出如下结论：

(1)在不同的丢包情况下能够保证系统的收敛性与稳定性。

(2)改进蝙蝠算法比基本蝙蝠算法在优化准确率以及优化速度上具有更好的效果。

(3)提出方法不仅可以抑制噪声信号，还能够提升故障状态和正常状态之间的区分度，使得阈值选择具有更大的容错范围与选择空间，有效改善各种故障类型的检测效果。