完全正则半群和幺半群上的Rees 矩阵半群

黎宏伟

（宿迁学院数学系，江苏 宿迁223800）

1 预备知识

其中 P =[ pλi],pλi∈ H1, λ , μ ∈Λ, i ,j ∈I,则S 关于此运算构成半群,称为幺半群上的Rees 矩阵半群,记作S = M [ A; I , Λ; P].设A 是含幺Clifford 半群, 则 S = M [ A; I , Λ; P]是含幺Clifford 半群上的Rees 矩阵半群.设含幺Clifford 半群A 是群{Ge|e ∈ E ( A)}的强半格,由文[3]知Se= M [ Ge; I , Λ; P]是含幺Clifford 半群上的Rees 矩阵半群S = M [ A; I , Λ; P]的子完全单半群,且S 是它的子完全单半群{Se}的强半格.根据文[3]的结论可知含幺Clifford 半群上的Rees 矩阵半群是完全单半群。

文[3]研究了含幺Clifford 半群上的Rees 矩阵半群S 的性质,给出了S 的正规加密群结构,指出正规加密群是含幺Clifford 半群上的Rees 矩阵半群当且仅当它是幺半群上的Rees 矩阵半群.由文[3]知正规加密群是一种特殊的完全正则半群,如果把正规加密群改为普通的完全正则半群,那么当幺半群上的Rees 矩阵半群是完全正则半群的时候, 它会是含幺Clifford 半群上的Rees 矩阵半群吗?本文对这个问题进行了研究,证明了下面的定理:

定理1 完全正则半群是含幺Clifford 半群上的Rees 矩阵半群当且仅当它是幺半群上的Rees 矩阵半群.

2 几个引理

设S 是完全正则半群,则S 是它的子完全单半群{Sα=M [Ge; Iα, Λα; Pα]|α ∈ Y }的半格,即 S =(Y , Sα),其中e 是群Ge 的单位元,则可以证明下面的引理.

引理1 设完全正则半群S 是它的子完全单半群{Sα=M [Ge; Iα, Λα; Pα]|α ∈Y }的半格, 且S 是幺半群上的Rees 矩阵半群,即 S = M [ A; I , Λ; P],其中A 是幺半群,则Iα= I ,Λα=Λ.

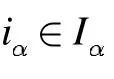
但 Sα是S 的子完全单半群,而 ( a , iα, λ )∈Sα,故( a , iα, λ)∈ S,这与 ( a , iα, λ )∉S矛盾.故假设不成立,即Iα⊆I.

再证 Iα= I.假设 Iα≠ I,则存在 i。 ∈I,但 i。 ∉Iα.

设(i, λ )∈ Iα×Λα,显然 (i 。 , λ )∉ Iα×Λα.于是任意的 a ∈ Ge,有 ( a , i。 , λ )∉Sα，但 ( a , i。 , λ )∈S.

故( a , i。 , λ ) L ( a , i, λ).

由[4]知 ( a , i。 , λ ) J ( a , i, λ).

由于 Sα是S 中的J 类且 ( a , i, λ)∈Sα，故( a , i。 , λ )∈Sα.这与 ( a , i。 , λ )∉Sα矛盾。

故假设不成立，于是可得 Iα= I.同理可证 Λα=Λ.引理1 得证。

引理2 设 Sα= M [Ge; I , Λ; Pα]是S = M [ A; I , Λ; P]任一J 类,则

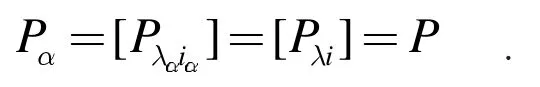
由引理2 可知S 任一J 类可以表示为

Sα= M [Ge; I , Λ; P].

引理3 设完全正则半群S 是幺半群上的Rees 矩阵半群,即S = M [ A; I , Λ; P],其中A 是幺半群,且S 是它的子完全单半群 {Sα= M [ Ge; I , Λ; P] |α ∈ Y }的半格,则A 是{Ge}的不交并集。

证明:由[4]知S 是它的子完全单半群 {Sα}的并集,从而可得A 是 {Ge}的并集。设

Sα= M [Ge; I , Λ; P]和Sβ= M [Gf; I , Λ; P]是S 的两个不同的子完全单半群,由[4]知 Sα和 Sβ的交集是空集,从而可得Ge和Gf的交集是空集.故A 是 {Ge}的不交并集.

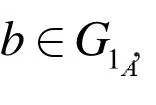
由于 Sα和 Sαγ是S 中的J 类, ( a , i , λ)∈Sα且( a , i, λ )∈ Sαγ,故 Sα和 Sαγ是S 中的同一个J 类,即Sα= Sαγ.由 (b a , i, λ )∈ Sαγ可得 ( ba , i, λ )∈Sα,于是ba ∈ Ge.同理可证 ab ∈Ge.引理4 得证.

设Sα=M [Ge; I , Λ; P ], Sβ=M [Gf; I , Λ; P]是S = M [ A; I , Λ; P]的两个J 类.

引理5Sαβ= M [Gef; I , Λ; P]

证明:设 Sαβ= M [Gh; I , Λ; Pαβ],

( a , i, λ) ∈Sα,( b, i, λ)∈Sβ.

设x =(e f )-1∈Gh,则(e f ) x = efx = h, x( e f )= xef =h 由( fxe)2=f ( xef )xe = fhxe =fxe知fxe 是Gh中的幂等元,因此, fxe =h.由于

( ef )( fxe) ( ef ) = ef2xe2f = efxef = e( fxe) f = ehf =ef,( fxe) (e f )( fxe) = fxe2f2xe = fxefxe = ( fxe)2=fxe,故ef = ( fxe)-1= h-1=h .同理可证fe=h.故Sαβ= M [Gh; I , Λ; Pαβ] = M [Gef; I , Λ; Pαβ].

3 证明定理1

(⇒ )设S 是完全正则半群, 若S 是含幺Clifford 半群上的Rees 矩阵半群，则S 显然是幺半群上的Rees 矩阵半群.

(⇐ )设S 是完全正则半群, 且S 是幺半群上的Rees 矩阵半群,即 S = M [ A; I , Λ; P],其中A 是幺半群,其单位元是1A.由S 是正则半群知A 是正则半群.

由引理3 知A 是子群 {Ge}的不交并集,下证A 是子群{Ge}的半格。

设Sα=M [Ge; I , Λ; P ], Sβ=M [Gf; I , Λ; P]是

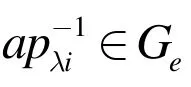
由文[6]知A 是Clifford 半群,又因为A 是幺半群,故A 是含幺Clifford 半群, 进而可得 S = M [ A; I , Λ; P]是含幺Clifford半群上的Rees 矩阵半群.定理1 得证。