主并合星系对SFR的增幅与其他参数关系的研究
2020-09-28邱佳杰孙艳春
邱佳杰 孙艳春
(北京师范大学天文系北京100875)
1 引言
星系是宇宙的重要组成部分, 它们是包含恒星、气体、尘埃等成分的引力束缚系统. 星系中的恒星形成是星系演化的直接驱动因素之一. 而量化星系当前恒星形成的关键参数, 是星系内的恒星质量(M∗)与恒星形成率(SFR). 它们是星系的两个最基本物理参数[1–2].
由于宇宙中的星系并非孤立存在, 许多星系之间的相互作用无法忽略, 因此, 星系的演化过程不仅受到星系本身恒星质量以及恒星形成率的影响, 同时还受制于星系的外部环境[3–4]. 这两者并不完全独立, 而是存在相互关联, 但在不同环境中(星系团与星系群、星系对以及孤立星系环境), 不同影响占据主导作用[5–9]. 在孤立星系环境中, 星系演化过程主要受到星系本身的影响, 而外部环境的影响通常可以忽略[8]. 与之相反的是星系团环境, 所有星系构成了一个统一的星系团环境, 同时, 外部环境对每个星系都施加影响, 使得环境影响与星系的性质存在强烈相关性.
星系对环境介于以上两种环境之间, 仅有两个存在强烈相互作用的星系, 它们以星系本身的影响为主, 同时需要考虑外部环境影响[9]. 与星系团环境不同的是, 由于星系对仅包含两个星系(目标星系与伴星系), 星系所处环境相对简单, 使得外部影响易于度量.通常情况下, 在星系对的研究中, 需要考虑的外部环境参数主要包括星系对之间的投影距离[10–12](投影距离是真实距离在天球上的投影, 两者之间存在函数关系, 真实距离无法准确测量), 伴星系的恒星质量或光度、形态类型等[9].
另一个需要考虑的影响星系对恒星形成的物理量, 是星系对之间的相对倾角(relative inclination), 其定义是两个盘星系的盘的法线之间的夹角. 选择这一参数的原因是, 它可能不仅与星系间的相互作用有关, 同样与局部大尺度结构有关. Wang等[13]对星系群中的小质量盘星系进行研究, 发现这些星系的朝向存在规律性. 他们认为这一规律与宇宙中的纤维(filament)结构有关. Lee等[14]则通过对一些星系以及它们的邻近星系(2000 kpc以内)的研究, 发现这些星系的旋转轴方向显著受到邻近星系运动的影响. 而更早的时候, Tempel等[15]研究了星系所处位置与大尺度中宇宙纤维状结构之间可能存在的关系. 因此, 尽管这些研究主要针对的是大尺度结果, 但是我们将尝试在更小尺度的星系对上, 讨论这些规律是否存在.
由于可以相对准确地测量出星系本身与外部影响, 星系对成为研究星系之间相互作用的重要研究对象[10–12]. 而主并合星系对是星系对的一种, 指星系对中两个星系的恒星质量相近(根据不同文献有不同定义, 常见的恒星质量之比小于3:1、4:1以及10:1)[13,16–17]. 主并合星系对从开始相互作用直至完全成为一个星系的过程称为主并合过程. 主并合过程是低密度环境中星系主要的外部环境演化过程, 对星系演化有明显作用, 是星系并合演化的主要研究对象[18–19]. Patton等[19]与Pearson等[20]的研究表明,主并合过程能使得星系的SFR相对于孤立星系平均有所增加, 并且这种影响可以扩展到星系相距约2000 kpc的范围. 此外, 由于银河系与仙女座星系处于主并合过程的最初阶段(相距约800 kpc, 并且相互靠近), 对观测到的主并合星系的研究可以用来推断未来数千万年发生在本星系群中的星系动力学过程[21–22].
本文旨在研究对于不同恒星质量的盘主导(disk-dominated)星系, 其主并合过程(具体地说, 是指星系从相距约200 kpc开始发生显著的相互作用, 直至星系盘明显发生形变或星系之间物质交汇为止[20])中, 星系对之间的投影距离与星系对之间的相对倾角、星系恒星形成率的增幅(即主并合过程中星系的恒星形成率与对照的孤立星系恒星形成率之间的差异)之间的关系. 在这些关系中, 除了相对倾角外, 其他参数都已经得到研究.例如, Ellison等[10]与Pearson等[20]都给出恒星质量与恒星形成率增幅之间的正相关性,Patton等[12]与Ellison等[23]则发现, 除了最小投影距离处恒星形成率的增长外, 更大投影距离的增幅不明显.
本文的结构如下: 第2节给出星系数据来源, 并通过判据选择出目标星系, 得到所需的相关物理性质参数; 在第3节中, 结合机器学习方法, 我们对物理参数进行分析, 并得到它们之间的相关性; 在第4节中, 我们分析了这些关系形成的可能原因, 并给出未来的研究方向.
2 星系数据的获取与处理
星系的基本参数来自GSWLC (GALEX SDSS WISE Legacy Catalog), 包含约700000个0.10z0.30且r波段星等小于18星系的信息[24], 其中z表示红移. 这些星系的坐标参数(赤经α、赤纬δ), 5个波段(u、g、r、i、z)以及Hα等发射线的流量来自斯隆数字巡天(Sloan Digital Sky Survey, SDSS)[25]. 除此以外, 星系演化探测器(Galaxy Evolution Explorer, GALEX)与广域红外巡天探测卫星(Wide field Infrared Survey Explorer, WISE)分别给出紫外波段(远紫外波段FUV与近紫外波段NUV)与红外波段(3.4µm、4.6µm、12µm以及22µm)的流量[26–27].
2.1 恒星质量与恒星形成率数据的获取
GSWLC数据集通过CIGALE(Code Investigating Galaxy Emission)软件,使用光谱能量分布(Spectral Energy Distribution)方法,直接提供了星系的恒星质量lg(M∗/M⊙)与恒星形成率lg[SFR/(M⊙·yr−1)], 恒星形成率在之后直接使用SFR表示[28].
2.2 视向速度与投影距离的计算
在接下来的星系对选择与参数获取中, 两个星系之间的投影距离∆D/kpc以及视向速度v/(km·s−1)[29]需要得到确定. 其中在计算投影距离前需要先计算每个星系的角直径距离DA/kpc. 星系的角直径距离, 两个星系之间的投影距离以及视向速度的定义如下:
角直径距离:
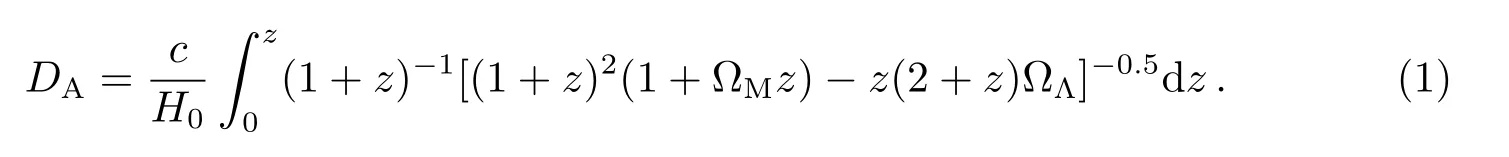
在标准宇宙学模型中, 宇宙学常数为ΩΛ= 0.7, 物质密度为ΩM= 0.3, 哈勃常数为H0=72 km·s−1·Mpc−1, 光速c= 299792.458 km·s−1.
两个星系之间投影距离:
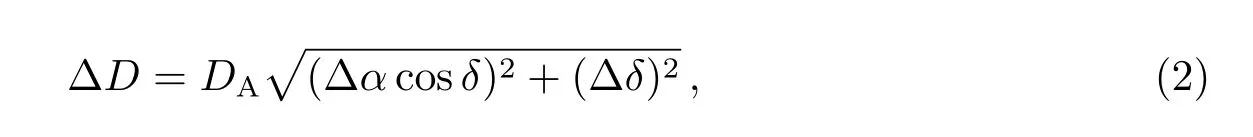
其中δ是星系赤纬, ∆α与∆δ分别是两个星系赤经与赤纬之差.
视向速度:

2.3 主并合星系对的选择与恒星形成率增幅的计算
选择主并合星系对的原因是, 目标星系的恒星形成率不仅受到星系本身性质的制约, 同样受到星系对中的伴星系的强烈影响. 如果主并合星系对周围还有其他星系, 那么外部影响将会难以度量. 因此, 主并合星系对的选择需要考虑以下这些因素[3–4].
首先, 经验上认为, 对于存在相互作用的两个星系, 它们的视向速度之差小于一定范围(经验范围200–2000 km·s−1), 取1000 km·s−1[29]; 其次, 由于一些研究表明投影方向上星系之间的相互作用可以一直影响到约2000 kpc的范围, 星系对所处环境不能是星系团或星系群环境, 需要处于低密度环境(经过星系群环境与经验认定, 要求在2000 kpc范围内星系数量N210)以及目标星系与最近伴星系的投影距离较小, 与其他星系的投影距离相对较大(目标星系与伴星系的投影距离rp(即, 上一小节中的∆D)不能超过与其他星系中最近星系的投影距离r2的10%, 这时可以认为其他星系的影响可以忽略不计); 最后,根据主并合的定义, 伴星系恒星质量M′∗与目标星系恒星质量M∗之比需要受到限制(选取10:1)[19].
最终, 主并合星系对样本的限制条件如下:
(1)视向速度之差: ∆v1000 km·s−1;
(2)伴星系投影距离:rp0.1r2且rp200 kpc;
(3)低密度环境:N210;
(4)星系对的恒星质量之比: 0.1M′∗/M∗10;
其中, 投影距离rp不仅是主并合星系对的判据之一, 同时是主要的研究对象.rp与r2均使用2.2节中的投影距离∆D计算得到.
为了计算恒星形成率的增幅, 需要选择一个孤立星系样本作为对照, 将目标星系的恒星形成率与孤立星系的恒星形成率之差作为恒星形成率的增幅. 这些孤立星系除了没有伴星系之外, 其他性质与目标星系相似. 当这些性质的差异小于一定范围时, 可以认为目标星系恒星形成率的增长主要是由伴星系的存在导致的[19].
主并合星系对与对照星系的选择见图1, 在图1中, 左图表示在主并合星系对中的目标星系(中心点)与伴星系(邻近中心的点)以及其他星系(左下点). 右图表示无伴星系的对照星系(中心点). 其中目标星系与伴星系的投影距离应小于200 kpc(左图圆圈).

图1 主并合星系对与对照星系的选择Fig.1 The selection of major-merger pairs of galaxies and compared galaxies
对照星系4个性质(z、lgM∗、N2、r2)的匹配容忍度如下. 最大红移差异∆z= 0.01;最大恒星质量差异∆lgM∗= 0.1; 低密度环境中星系数量N2差异小于10%; 其他星系最近距离r2差异小于10%. 由于不同星系的这4个性质存在差异, 对于每个主并合星系对中的目标星系, 要求至少有10个不同对照星系, 以减小随机误差对恒星形成率的影响.
每个目标星系的所有对照星系需要进行加权平均, 以得到与目标星系数量相同的对照样本. 假设一个目标星系(其参数表示为z、lgM∗、N2、r2以及SFR)有N个对照星系,其中第k个对照星系的主要参数为zk、lgMk、N2k、r2k以及SFRk. 那么加权平均过程如下:
红移权重(∆z=0.01, 其余3个参数计算权重的方法完全相同):

第k个对照星系的总体权重:

对于对照样本的恒星形成率, 可以通过下式构建:

其中SFRk是每个对照星系的真实SFR, SFRc是对照样本构造的SFR. 恒星形成率增幅可以使用∆SFR=SFR−SFRc得到.
2.4 盘主导星系的目视检查与倾角计算
上一节筛选出处于主并合星系对中的目标星系. 由于涉及到主并合星系对之间的相对倾角, 因此, 目标星系与伴星系都需要进行光谱与图像的目视检查, 并通过星系图像计算相对倾角. SDSS的光谱与图像可以用来去除不符合条件的星系, 仅保留目标星系与伴星系均为盘主导星系的样本.
盘主导星系的特征包括: 星系图像整体呈现清晰完整、没有重叠的盘状, 盘上有旋臂结构, 盘中心没有核球或者核球不明显; 星系光谱以窄的发射线为主, 没有明显吸收线. 需要说明的是, 早型盘主导星系由于存在明显的核球以及缺乏气体, 予以去除.
盘主导星系之间的相对倾角∆i计算方式如下:
首先, 测量单个星系的旋转轴相对于视线方向的倾角1方法同Galaxy Inclination Zoo, 网址http://edd.ifa.hawaii.edu/inclination/index.php. 通过测量SDSS星系图像的短轴b与主轴a之比b/a, 可以计算出星系盘的法线相对于视线方向的倾角[25]. 计算公式如下:

其中b/a是星系的短轴与主轴之比, 即轴比. 由于盘主导星系存在一定厚度, 因此观测到的盘主导星系最小的b/a不为0. 使用的定义为, (b/a)min= 0.2表示侧向星系[30–31];
其次, 星系之间的相对倾角计算需要知道单个星系的主轴方向, 因此在本文中统一测量了星系的主轴相对于图像正东方向的方位角α. 结合倾角i, 可以计算出目标星系与伴星系之间的相对倾角∆i:
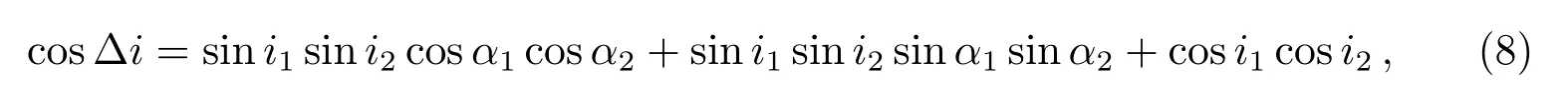
其中, 目标星系与伴星系的下标分别是1与2. 盘主导星系对相对倾角的计算如图2,a1、b1、α1、i1分别表示目标星系的主轴、短轴、方位角与倾角;a2、b2、α2、i2则分别是伴星系的主轴、短轴、方位角与倾角.此外, 图2呈现十字四周围4个字母(N、E、S、W)分别表示天球上北、东、南、西4个方位.
图2左侧目标星系的b/a= 0.2 (侧向星系), 伴星系的b/a= 1 (正向星系). 目标星系α1= 25◦, 伴星系α2= 0◦. 那么根据相对倾角的计算公式可以得到∆i= 90◦, 即这两个星系盘之间相互垂直. 与左侧示意图相似, 右侧目标星系b/a= 0.8与α1= 12.5◦, 伴星系b/a= 0.5与α2= 50◦, 可以得到∆i= 37.2◦. (在计算相对倾角时, 使用这种方法无法区别例如i= 30◦与i=−30◦的情况, 使得最终计算得到的∆i存在误差. 但这并不显著影响∆i的整体趋势.)

图2 盘主导星系对相对倾角的计算Fig.2 The calculation of the relative inclination in disk-dominated galaxy pairs
最后得到163个目标星系, 主要参数范围如下: 0.02z0.2、9.0lgM∗11.5、0rp200 kpc、0∆i90◦、−0.5∆SFR2.0. 这些星系均有活跃的恒星形成活动(如图3).

图3 GSWLC数据集中星系的M∗与SFR的分布Fig.3 The distribution of galaxies’ M∗and SFR in the GSWLC dataset
在图3中展示GSWLC数据集中所有星系样本(轮廓线)与目标星系(黑点)在SFRM∗图中的分布. 所有星系样本呈现双峰分布, 其中上部是恒星形成率较大的恒星形成星系区域, 下部是恒星形成率接近于零的宁静星系区域. 而目标星系全部位于恒星形成星系区域内.
3 主并合星系对物理性质的关系及其分析
3.1 机器学习方法分析物理性质之间的关系
首先使用随机森林(RF)与相关系数矩阵的方法, 对所有数据进行分析. 随机森林的特征重要性是指在随机森林回归的机器学习训练过程中, 这4个物理性质对训练结果(即,∆SFR)的影响程度. 特征重要性最大的性质对机器学习的过程影响最大, 说明其重要程度最高. 从表1中可以看出, lgM∗对于∆SFR几乎有决定性的影响作用. 在其余3个物理性质中, ∆i有相对重要的影响程度, 而对于rp与z, 它们则相对不重要.

表1 4个物理性质在RF过程中的特征重要性Table 1 Feature importance of four properties in random forest processes
然后, 给出这4个物理性质的相关系数矩阵以表示不同性质之间的关系. 表2的相关系数显示, 除了z与lgM∗之间存在强相关性, 其他物理性质之间几乎没有相关性. 而在这4个物理性质与∆SFR之间的相关系数中, 只有rp与∆SFR之间没有相关性. 0.8–1.0为极强相关, 0.6–0.8为强相关, 0.4–0.6为中等程度相关, 0.2–0.4为弱相关, 小于0.2为不相关.

表2 4个物理性质以及∆SFR的皮尔逊相关系数矩阵Table 2 Pearson correlation coefficient matrix of four properties and ∆SFR
需要说明的是,z与lgM∗之间存在强耦合(SDSS观测的选择效应[25]). 由于lgM∗的特征重要性更高, 而z的特征重要性很低, 因此可以认为,z与lgM∗的相关性导致z与∆SFR之间存在弱正相关性, 可以只考虑lgM∗. 接下来的几个小节将分析lgM∗、rp与∆i对∆SFR的影响.
3.2 恒星质量与恒星形成率增幅的关系
星系的恒星质量是星系最重要的物理参数之一, 恒星质量与恒星形成率之间的关系在天体物理研究中有着非常重要的作用. 图4给出了目标星系的恒星质量与恒星形成率增幅之间的关系, 其中空心点表示lgM∗相差0.5的间隔范围内的平均数据, 横轴方向误差棒表示每个bin取值的范围, 纵轴方向误差棒表示该bin内数据的标准差. 在lgM∗∈[9,−9.5]与lgM∗∈[11,−11.5]的范围内, 目标星系的数量相对较少, 统计误差可能较大.

图4 目标星系的lg M∗与∆SFR之间的关系Fig.4 The relation between lg M∗and ∆SFR in the chosen galaxies
在主并合星系对中, 目标星系的恒星形成率增幅与其恒星质量存在强正相关性(皮尔逊相关系数0.60). 对于lgM∗= 9.25的低质量星系, 平均恒星形成率增幅仅为∆SFR= 0.14; 而对于lgM∗= 11的大质量星系, 可以达到0.96. Ellison等[10]使用B波段绝对星等MB作为恒星质量的替代, 给出了相似的结果. Pearson等[20]则使用SDSS、KiDS (Kilo Degree Survey)以及CANDELS (Cosmic Assembly Near-infrared Deep Extragalactic Legacy Survey)这3个数据集, 同样发现并合星系恒星形成率的增长与恒星质量存在正相关性. 这一关系的可能原因是, 对于更大质量的盘星系, 它们含有更多的气体. 如果所有目标星系有相同恒星转化效率, 则更大质量的盘星系可以达到更高的恒星形成率增幅.
3.3 投影距离与恒星形成率增幅的关系
图5给出了主并合星系对之间的投影距离与目标星系恒星形成率增幅之间的关系.其中空心点表示rp相差30 kpc的间隔范围内的平均数据, 横轴方向误差棒表示每个bin取值的范围, 纵轴方向误差棒表示该bin内数据的标准差. 在rp超过150 kpc的范围, 目标星系的数量相对较少, 统计误差较大.
由于本文研究的是没有明显发生形变或物质交汇的主并合星系对, 研究的结果发现这些主并合星系对之间的投影距离与目标星系恒星形成率增幅之间不存在相关性. 平均恒星形成率增幅在所有范围内的变化基本不超过0.3. 我们得到的结果与Ellison等[23]给出的结果相似, 但他们使用的投影距离范围仅是rp∈[0–80]kpc. Patton等[12]在投影距离rp∈[0–200]kpc范围内进行了类似的研究, 但他们的样本包含明显发生碰撞的星系.他们的结果表明, 当rp不超过50 kpc时, 恒星形成率明显增加.

图5 目标星系的rp与∆SFR之间的关系Fig.5 The relation between rp and ∆SFR in the chosen galaxies
3.4 相对倾角与恒星形成率增幅的关系
图6给出了相对倾角与恒星形成率增幅之间的关系. 其中空心点表示∆i相差15◦的间隔范围内的平均数据, 横轴方向误差棒表示每个bin取值的范围, 纵轴方向误差棒表示该bin内数据的标准差. 由于定义(b/a)min= 0.2, 使得图上出现一系列竖直排列的点. 但这些点并不显著影响结论.

图6 目标星系的∆i与∆SFR之间的关系Fig.6 The relation between ∆i and ∆SFR in the chosen galaxies
在主并合星系对中, 主并合星系对之间的相对倾角与目标星系恒星形成率增幅之间确实存在一定联系(皮尔逊相关系数−0.40, 弱相关). 在两个星系的盘接近相互垂直时,∆SFR = 0.39; 但是在两个星系的盘接近相互平行时, ∆SFR = 1.00.
这一结果可能表明, 相对倾角与恒星形成率增幅之间的关系可能是由星系间的相互作用(Cen等[32]与Zhang等[33]的讨论)以及局部大尺度结构(Wang等[13]与Tempel等[15])引起的. Cen等[32]使用高分辨率宇宙流体动力学模拟, 发现星系恒星成分的旋转方向与星系相互作用有关. 对于后者, 我们尝试将样本星系与Tempel等[15]给出的位于纤维状结构附近的星系进行匹配(他们给出了这些星系与纤维状结构的最近距离). 但受限于本文中的样本星系数量, 匹配得到的结果无法呈现这一相对倾角与最近纤维距离的关系. 我们将在接下来的工作中给出两者之间的关系, 如果在不同最近纤维距离的范围内, 相对倾角的分布呈现一定规律, 那么这一结果可以印证我们的结论.
4 讨论与结论
本文通过GSWLC数据集, 得到主并合星系对样本, 并研究了样本中目标星系的lgM∗、rp与∆i这些物理性质与∆SFR之间的关系.
使用随机森林特征重要性与相关系数分析, 得出以下结论:
首先, ∆SFR与lgM∗存在强正相关性, lgM∗相对较大的目标星系, 其∆SFR值更大.这一关系可能原因是, 恒星质量更大的目标星系, 本身含有更多的气体. 当它们处于主并合过程中时, 并合导致的气体扰动使得气体内流并在星系中心形成恒星. 在相同恒星形成效率的情况下, 气体内流并转化为恒星的质量更大, 因而可以产生更高的恒星形成率;
其次,在本文研究的没有明显发生形变或物质交汇的主并合星系对中,∆SFR与rp没有相关性,∆SFR在所有rp处没有显著差异. 结合Patton等[12]与Ellison等[23]提出的,在rp= 10 kpc处, 目标星系的恒星形成率可能有所增长以及本文图5中rp小于30 kpc的区间同样可能存在上升的趋势, 这可能意味着, 星系的主并合过程中, 星系恒星形成率的增长主要发生在非常小投影距离的范围内;
最后, ∆SFR与∆i存在弱的负相关性, 倾向平行(∆i= 0◦)的主并合星系对, 有更大的∆SFR. 这些结果产生的可能原因是相对倾角可能受到星系的相互作用与更大尺度环境的影响, 但这两方面的解释仍然需要进一步研究.
受限于星系性质的复杂性, 主要的研究参数仅包括恒星质量、投影距离、相对倾角以及恒星形成率的增幅, 并没有对其他重要的物理参数(例如金属丰度、气体分布等)进行讨论, 可能使得潜在的结论没有得到发掘; 由于观测数据处理的条件相对严格, 得到的目标星系数量较少, 这可能导致最后的结果与实际存在一定偏差; 另外, 星系的统计研究实际上是大量星系在某一时刻的快照(snapshot), 而非单个星系在主并合过程中的连续演化, 两者之间存在差异, 前者仅是后者的间接分析.
单个星系在主并合过程中的演化仅从观测上进行研究是不可能的, 需要使用马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)方法, 或者宇宙流体动力学模拟(例如: Illustris、Evolution and Assembly of GaLaxies and their Environments、Millennium Simulation Project等程序)的研究. 后者提供了一个更加可靠的方法研究主并合过程中星系的不同物理参数的变化[34–36].
在接下来的工作中, 我们的研究将主要集中到宇宙流体动力学模拟上, 以进一步揭示主并合过程对星系的巨大影响.
