五轴线性插补中进给速度的规划控制方法
2020-09-28陈良骥睢英照王中州魏广西
陈良骥,睢英照,王中州,魏广西
(天津工业大学机械工程学院, 天津 300387)
目前数控系统已经得到较快速的发展,为高效地获得高精度加工零件,国内外研究者已越来越重视数控系统在刀具进给速度控制方面功能的开发和研究工作[1-5].刀具进给加减速控制是实现高速、高精数控加工的重要环节之一.按照与轨迹插补的时间先后顺序,加减速控制可分为前加减速控制[6-8]和后加减速控制[9].后加减速控制是一种插补点位置数据获得后再调整插补步长的速度规划方式,容易产生插补点处的位置误差.前加减速控制则是在插补之前按照给定的速度变化规律调整好插补步长后再插补计算出插补点位置数据,更能有效保证插补点的位置精度.因此,前加减速控制方式在数控系统有关加减速控制中研究得更为广泛.
使用前加减速控制方式在对进给速度规划处理时,一般会将每个插补路径段的加工执行时间规划处理为数控系统采样插补周期的整数倍,此时如果插补步长的计算不准确,往往会导致难以真正将刀具控制到插补路径的终点位置,产生终点位置偏差,降低路径插补控制的精度.
国内外研究学者已提出了多种加减速规划控制方法,主要有以下几种:梯形加减速[10]、“S”型加减速[11-12]、指数型加减速[13]、三角函数加减速[14]和三次多项式加减速[15-16].王宇晗等[17]通过实时前瞻当前插补点与插补路径段的终点间距离来判断减速点的位置,但该方法存在距离计算误差及实时插补计算量等问题.Leng等[18]根据数据采样插补的离散特性,建立了加减速控制离散数学模型,得到了理论减速长度的离散表达式,同时针对加减速控制插补前难以预先确定减速点的问题,从理论减速长度的表达式出发,推导出自适应加减速控制算法.Zhang等[19]通过求解二阶微分方程,给出了脉冲达到极限时速度函数的表达式,提出了一种最优的约束进给量规划算法.赵翔宇等[20]提出了一种三次S曲线加减速算法,给出了相应的加加速度、加速度、速度和位移的数学表达式,对数控加工中各种情况进行了速度规划.综上所述,以上方法均可以有效规划数控加工过程中的速度,但是其算法实现过程相当复杂,涉及到多个计算参数,需要花费大量的时间去计算.前加减速规划都是采用离线的方式进行计算,当一些计算参数发生变化时,数控机床很难及时地做出响应.再者目前相关学者大多是对机床的平动轴速度进行最大值限制,而忽略了旋转轴的速度极限,导致数控机床在加工过程中旋转轴速度超过极限值,对机床产生冲击,缩短机床寿命,产生较大的表面误差,无论是在加工效率方面还是在加工精度方面都还存在一些弊端.
针对当前相关研究存在离线算法的复杂性及忽略旋转轴速度按比例分配时角速度、角加速度超限等方面的问题,本文拟采用计算简单、易实现、加工效率较高的梯形加减速模型规划数控加工中的进给速度,该方法无须预测减速点且能够精确加工到加工路径段的终点,同时对旋转轴的角速度、角加速度增加极限值约束,可使平动轴与旋转轴平稳协调运动,能极大地避免刀具速度超限引起的轮廓误差,并减少对数控机床的冲击,提高机床在轨迹插补控制方面的精度.
1 梯形加减速控制算法模型
梯形加减速控制算法是在所有速度规划模型中计算量最小、效率最高的控制模型,它一般分为3个阶段:匀加速阶段、匀速阶段、匀减速阶段.在匀加速阶段,机床控制刀尖点以机床允许的最大加速度进行加速,直到速度达到插补路径段指定的进给速度后开始控制刀尖点匀速进给,然后再以机床允许的最大加速度开始减速,直到到达插补路径段的终点时结束.设Vmax为指定进给速度,Vs为起始速度,Ve为终止速度,ta为加速阶段时间,tc为匀速段时间,td为减速度段时间,如图1所示.
2 平动轴的运动学约束控制
2.1 最大速度可以达到Vmax
若在加工过程中速度可以达到指定进给速度Vmax,则完全符合如图1所示的梯形加减速控制模型.设机床所能承受的最大加速度为amax,插补路径段的总长度为l,机床的插补周期为T,加速周期数为Na,匀速周期数为Nc,减速周期数为Nd.则
加速时间
(1)
加速周期数
(2)
减速时间为
(3)
加速段和减速段总的位移为
(4)
若l>D,则存在匀速段,匀速段时间为
(5)
匀速周期数为
(6)
匀速段的位移为
Sc=NcTVmax
(7)
加速段、匀速段和减速段的总位移为
Sz=D+Sc
(8)
由于周期数规划时,采用的是取整运算,因此加工路径可能会产生残余,残余的长度为
De=l-Sz
(9)
减速段最后一个周期的速度
Vl=Vmax-NdTamax
(10)
将残余距离以一个平均速度ΔV分配到减速段的每个周期内,但要保证减速段的最后一个周期的加速度要小于amax,即
(11)
若式(11)成立,则
(12)
若式(11)不成立,需要减速段增加一个周期,则重新规划
(13)
综上可得每个周期内的速度
Vi=
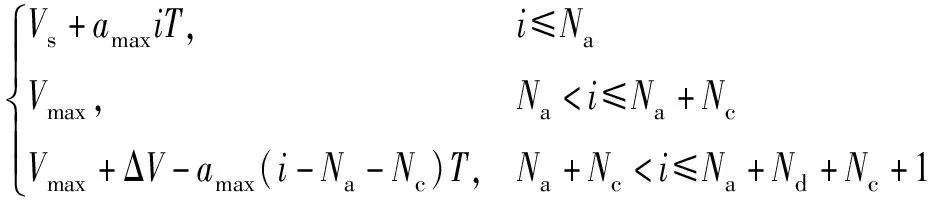
(14)
2.2 最大速度V′max当最大速度达不到Vmax时,加工过程只存在加速段和减速段,其速度模型如图2所示.
计算能达到的最大速度V′max
(15)
解得
(16)
加速段的周期数
(17)
减速段周期数
(18)
由公式(4)可得,残余长度为
De=l-D
(19)
减速段最后一个周期的速度为
Vl=V′max-NdTamax
(20)
同理判断式(11)是否成立得到式(12)(13),每个周期的速度为
Vi=
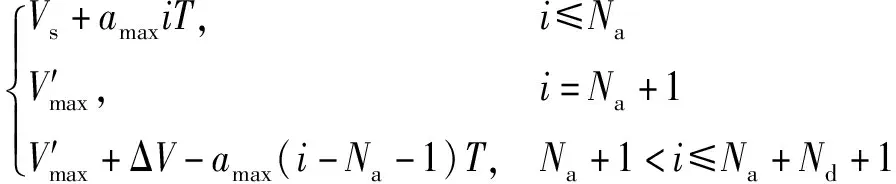
(21)
2.3 加工段只存在加速段
当Ve>Vs时,加工段只存在加速过程,速度模型如图3所示.
加速段周期数为
(22)
加工的位移为
(23)
残余长度如式(19)所示,加速段最后一个周期的速度为
Vl=Vs-NaTamax
(24)
同理判断式(11)是否成立,若成立得到式(12),若不成立则重新规划
(25)
则每个周期的速度为
Vi=Vs+ΔV+amaxiTi≤Na
(26)
2.4 加工段只存在减速段
当Vs>Ve时,加工段只存在减速过程,速度模型如图4所示.
加速段周期数为
(27)
加工的位移为
(28)
残余长度如式(19)所示,减速段最后一个周期的速度为
Vl=Vs-NdTamax
(29)
同理判断式(11)是否成立,若成立得到式(12),若不成立则重新规划
(30)
则每个周期的速度为
Vi=Vs+ΔV-amaxiTi≤Nd
(31)
平动轴的速度规划流程图如图5所示.
3 旋转轴的运动学约束控制
五轴数控机床平动轴与旋转轴在运动形态方面的差异,直接导致2种进给伺服轴在运动时所能承受的最大速度、最大加速度也不同.然而,传统速度规划方法并未深入考虑上述差异性,仍然沿用平动轴最大速度、加速度极限去规划旋转轴的转动角速度和角加速度,这将可能导致旋转轴角速度、角加速度超出机床旋转轴的最大可承受角速度、角加速度极限范围,换句话说也就是转动跟不上平动,结果必然是平动轴与旋转轴之间的运动不协调,不协调运动又会产生机械冲击,加工工件时可能发生过切现象,影响加工表面质量和精度.为避免平动轴与旋转轴之间的运动不协调情况发生,本文增加对旋转轴的角速度及角加速度的动力学约束条件,提出如下旋转轴角速度、角加速度控制方法.
3.1 平动轴可达到的最大合成进给速度
经过第2小节的速度规划后,假设在第m个插补周期时,平动轴具有最大合成进给速度,本文中将其定义为Vm,根据前述分析,显然有Vm≤Vmax成立.以A-C型双摆头五轴数控机床为例,根据五轴线性插补原理可知,在第m个插补周期内有
(32)
成立.式中:Δlm为平动轴在第m个插补周期的合成位移;ΔAm为A旋转轴在第m个插补周期的角位移;ΔCm为C旋转轴在第m个插补周期的角位移;VAm为A旋转轴在第m个插补周期的角速度;VCm为C旋转轴在第m个插补周期的角速度.
式(32)中的旋转轴角位移ΔAm和ΔCm可按照以下线性比例进行分配获得:
(33)
式中:l为当前插补路径段的总长度;As为A旋转轴在当前插补路径段的起点坐标;Ae为A旋转轴在当前插补路径段的终点坐标;Cs为C旋转轴在当前插补路径段的起点坐标;Ce为C旋转轴在当前插补路径段的终点坐标.
式(33)中ΔAm和ΔCm分别与(Ae-As)和(Ce-Cs)取得相同的符号.
3.2 旋转轴角速度约束控制
由式(32)和(33)可知,平动轴在第m个插补周期达到Vm的进给速度时,A、C旋转轴角速度的绝对值也将分别达到最大值|VAm|和|VCm|,只要控制|VAm|和|VCm|均在机床旋转轴可承受的角速度约束范围内即可.
根据式(32)和(33),可推导出第m个插补周期内平动轴的合成进给速度Vm与A、C旋转轴的角速度VAm、VCm的关系式
(34)
假设五轴数控机床A、C旋转轴的最大极限角速度约束分别为VAmax和VCmax(机床旋转轴无论正转还是反转,角速度约束应恒为正值,即VAmax和VCmax均大于0).对A、C旋转轴角速度约束控制计算过程如下.
1)根据式(34)计算出VAm和VCm,将结果分别表示为
VAm=sgn(VAm)abs(VAm)
VCm=sgn(VCm)abs(VCm)
式中:sgn(x)为取x符号的函数;abs(x)为取x的绝对值函数.
2)当abs(VAm)≤VAmax且abs(VCm)≤VCmax时,表示A、C旋转轴的角速度均未超出机床旋转轴最大极限角速度,同时也表明此时的平动轴与旋转轴均可在各自允许的极限速度范围内协调运动,第2小节中关于平动轴进给速度的规划结果满足旋转轴角速度约束控制要求.
3)当abs(VAm)>VAmax或abs(VCm)>VCmax时,表示之前在第2小节里规划计算得到的实际可达到的平动进给速度偏高,使得至少有1根旋转轴的角速度已超出该旋转轴最大可承受的极限角速度,此时超出角速度约束范围的旋转轴将出现与平动轴运动不协调一致的情况.为此,需降低实际可达到的平动进给速度,使得对应的旋转轴角速度被约束控制在机床旋转轴最大极限角速度以内.对此,本文提出如下重新规划计算方法.
① 平动轴最大合成进给速度的修调
对1根旋转轴的角速度超出该轴角速度极限约束范围的情形(不妨设为A轴),可以sgn(VAm)VAmax代替式(34)中的VAm,可求得新的平动轴最大合成进给速度
(35)
同理对2根旋转轴的角速度均超出各自角速度极限约束范围的情形,分别以sgn(VAm)VAmax和sgn(VCm)VCmax代替式(34)中的VAm和VCm,求得
(36)
此时应取(V′m)A和(V′m)C中较小者作为新的平动轴最大合成速度V′m,即
V′m=min((V′m)A,(V′m)C)
(37)
式中min(x,y)函数为返回x和y中较小的数.
② 平动轴进给速度的重新规划计算
根据式(35)~(37)计算获得平动轴新的最大合成进给速度V′m后,将第2小节中Vmax重新赋值为V′m,对平动轴的进给速度进行重新规划计算.
3.3 旋转轴角加速度约束控制
假设五轴数控机床A、C旋转轴的最大极限角加速度约束分别为aAmax和aCmax(aAmax和aCmax均为正数),在整个加工过程中,实际最大角加速度应不大于aAmax和aCmax.在任意的第i个插补周期,旋转轴角加速度的计算公式为
(38)
式中ai为平动轴在第i个插补周期的加速度.
根据式(38)可知,旋转轴的角加速度与平动轴加速度之间具有线性相关性,即当平动轴具有加速度时,旋转轴同时也将具有角加速度,而且有
(39)
式中:(aA)max为A旋转轴实际的最大角加速度;(aC)max为C旋转轴实际的最大角加速度.
(aA)max和(aC)max(都取为非负数值).对式(39)的运算结果作如下讨论:
1)当(aA)max≤aAmax且(aC)max≤aCmax时,表示A、C旋转轴的角加速度均未超出机床旋转轴最大极限角加速度,同时也表明如按照机床平动轴最大极限加速度amax进行速度规划,其计算结果可以满足旋转轴角加速度约束控制的要求.
2)当(aA)max>aAmax或(aC)max>aCmax时,表示至少有1根旋转轴的角加速度已超出该旋转轴最大可承受的极限角加速度,此时表明第2小节中如果继续按照机床平动轴最大极限加速度amax进行速度规划,将导致旋转轴角加速度超出相应的最大极限角加速度约束范围.因此,需在进行平动轴速度规划前重新计算新的平动轴最大加速度amax,本文采用如下方法对平动轴最大加速度amax进行修调.
① 当1根旋转轴的角加速度超出该轴角加速度最大极限约束时(不妨设为A轴),可以(aA)max代替式(38)中的aAi,解得新的平动轴最大加速度
(40)
② 当2根旋转轴的角加速度均超出各自角加速度最大极限约束时,可分别以(aA)max和(aC)max代替式(38)中的aAi和aCi,求得
(41)
取式(41)中(amax)A和(amax)C的较小者作为新的平动轴最大加速度amax,即
amax=min((amax)A,(amax)C)
(42)
将式(40)~(42)计算出的amax作为平动轴进给速度规划时的加速度约束参数使用.
4 进给速度规划控制流程
综上所述,本文在第2、3小节中分别详细介绍了关于平动轴运动学约束控制方法和旋转轴的运动学约束控制方法.平动轴进给速度规划控制的约束条件为最大速度和最大加速度,旋转轴进给速度规划控制的约束条件为最大角速度和最大角加速度.在进给速度规划时,必须同时满足所有的约束条件,否则会对机床产生冲击或加工工件产生过切和欠切现象.因此,规划进给速度时必须对超限的速度或加速度参数进行重新计算.现将五轴数控加工时机床运动学参数约束条件下的进给速度规划控制流程(控制流程图如图6所示)归纳总结如下:
1)用式(39)计算旋转轴A/C的最大角加速度(aA)max和(aC)max.
2)若(aA)max≤aAmax且(aC)max≤aCmax
① 以平动轴的最大加速度amax进行速度规划,同时计算出平动轴最大合成速度Vm;
② 用式(34)计算A/C的最大角速度VAm和VCm;
③ 当abs(VAm)≤VAmax且abs(VCm)≤VCmax时,转入第4)步;
④ 当abs(VAm>VAmax或abs(VCm)>VCmax时,用式(35)~(37)计算V′m;
⑤ 令Vmax=V′m,转入第4)步.
3)若(aA)max>aAmax或(aC)max>aCmax
① 用式(40)~(42)重新计算平动轴的最大加速度amax;
② 转入第2)①步.
4)按照第2小节中的方法进行平动轴速度规划(见图5).
5 实际数据仿真与结果分析
为了验证本文提出方法的有效性,选取数控加工文件中的2个相邻程序段作为待插补路径段进行速度规划计算,如表1所示.
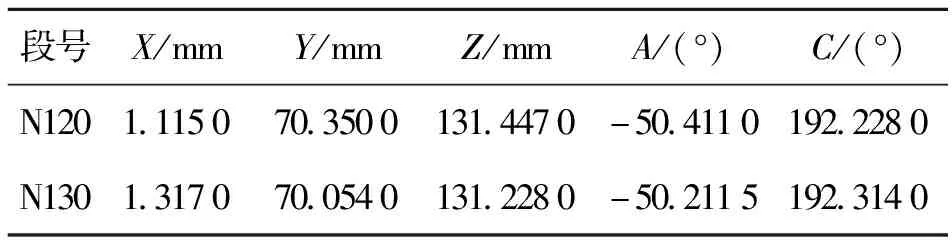
表1 相邻加工程序段数据
各类已知参数为:1)五轴数控机床相关的运动学约束参数,平动轴最大可承受的加速度amax=1 000 mm/s2,旋转轴的最大角速度为VAmax=VCmax=0.073 rad/s,最大角加速度为aAmax=VCmax=7 rad/s2;2)数控系统采样插补周期T=0.004 s;3)插补路径段起点线速度Vs=2 mm/s,终点线速度为Ve=4 mm/s;4)程序段指定的进给速度Vmax=12 mm/s.
使用本文提出的方法,平动轴合成进给速度曲线如图7所示.D点为预测加减速规划中的减速点,由于在速度规划中,周期数要进行取整,故实际的减速点并非D点,而是图中的D1点.理论减速点和实际减速点不重合,产生定位误差,导致实际不能达到插补路径段的终点,会产生残余位移,即图7中传统加减速规划速度曲线与本文加减速规划速度曲线所围成的面积.
为了避免产生残余距离,本文提出的方法可以提前规划好周期数,在规划好的周期内,将残余距离用一特定的速度分配到减速段的周期内,由于减速段每个周期都增加了一个速度,即在匀速段与减速段转接的这一周期加速度变小,其他周期加速度不变,因此本文的加减速规划控制方法不会导致加速度变大,该方法可不必预测减速点位置也能够精确到达插补路径段的终点,提高了位置控制精度.
以程序段指定的进给速度Vmax规划旋转轴的角速度、角加速度时,本文将旋转轴的最大极限角速度和最大极限角加速度作为速度规划的运动学约束条件.计算出的旋转轴角速度、角加速度若超出上述约束条件时,则以修改平动轴指定进给速度和最大可承受加速度amax的方式对进给速度进行重新规划控制,重新规划前后的旋转轴角速度曲线和角加速度曲线分别如图8、图9所示.
由修正前A轴角速度和角加速度曲线可知,A轴在修正前其角速度和角加速度都超出了旋转轴的最大角速度和角加速度限制,需要按照A轴的最大极限角速度和角加速度值来修正平动轴的指定进给速度和最大可承受加速度,修正后重新计算A轴的角速度和角加速度使其满足约束条件.由修正前C轴角速度和角加速度曲线可知,C轴在修正前其角速度和角加速度并没有超出旋转轴最大极限角速度和角加速度,但由于A轴的角速度和角加速度超限,重新规划使平动轴指定进给速度和最大可承受加速减小,同样也会使C轴的角速度和角加速度减小.
以满足旋转轴的最大极限角速度和最大极限角加速度约束条件的平动轴指定进给速度和最大可承受加速度来重新规划进给速度,重新规划前后的进给速度和加速度曲线分别如图10、11所示.可以看出修正后的进给速度和加速度都有所减小,这也将会增加插补周期数量.优点是有效避免了A轴对机床的冲击以及刀具对加工面产生的过切现象.
本文提出的加减速规划控制方法对五轴线性插补时的非线性误差的影响情况如图12所示.可以看出,在使用本文方法前的最大非线性误差为8,使用本文方法后的最大非线性误差为5,非线性误差降低了37.5%,表明本文提出的加减速控制方法仍能有效地提高加工表面的轮廓精度.
6 结束语
1)本文通过提前规划加减速周期,避免了预测减速点的难题,同时通过加工路径的前瞻运算,将剩余加工路径以某一速度平均分配到减速段的各个周期,从而使机床刀具精确地到达插补路径段的终点,提高加工精度.
2)分析传统旋转轴的速度按比例分配导致机床旋转轴会出现角速度、角加速度超过其最大值限制,机床不能平稳运动的问题,通过增加旋转轴的角速度、角加速度约束条件,提出速度修正算法来控制旋转轴的运动速度,从而使机床避免产生冲击,延长机床的使用寿命.
3)使用速度修正算法对平动轴的最大进给速度和最大加速度进行修正,通过Matlab软件进行实际数据仿真验证,非线性误差减小了37.5%,有效地提高了加工工件的精度.
当最大速度达不到Vmax时,加工过程只存在加速段和减速段,其速度模型如图2所示.
计算能达到的最大速度V′max
(15)
解得
(16)
加速段的周期数
(17)
减速段周期数
(18)
由公式(4)可得,残余长度为
De=l-D
(19)
减速段最后一个周期的速度为
Vl=V′max-NdTamax
(20)
同理判断式(11)是否成立得到式(12)(13),每个周期的速度为
Vi=
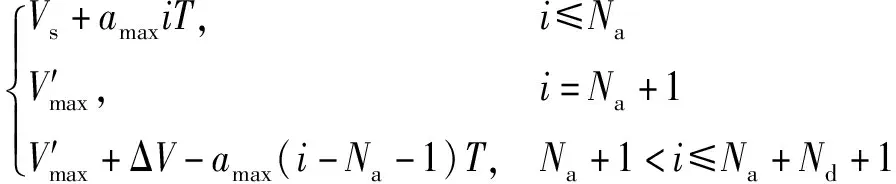
(21)
2.3 加工段只存在加速段
当Ve>Vs时,加工段只存在加速过程,速度模型如图3所示.
加速段周期数为
(22)
加工的位移为
(23)
残余长度如式(19)所示,加速段最后一个周期的速度为
Vl=Vs-NaTamax
(24)
同理判断式(11)是否成立,若成立得到式(12),若不成立则重新规划
(25)
则每个周期的速度为
Vi=Vs+ΔV+amaxiTi≤Na
(26)
2.4 加工段只存在减速段
当Vs>Ve时,加工段只存在减速过程,速度模型如图4所示.
加速段周期数为
(27)
加工的位移为
(28)
残余长度如式(19)所示,减速段最后一个周期的速度为
Vl=Vs-NdTamax
(29)
同理判断式(11)是否成立,若成立得到式(12),若不成立则重新规划
(30)
则每个周期的速度为
Vi=Vs+ΔV-amaxiTi≤Nd
(31)
平动轴的速度规划流程图如图5所示.
3 旋转轴的运动学约束控制
五轴数控机床平动轴与旋转轴在运动形态方面的差异,直接导致2种进给伺服轴在运动时所能承受的最大速度、最大加速度也不同.然而,传统速度规划方法并未深入考虑上述差异性,仍然沿用平动轴最大速度、加速度极限去规划旋转轴的转动角速度和角加速度,这将可能导致旋转轴角速度、角加速度超出机床旋转轴的最大可承受角速度、角加速度极限范围,换句话说也就是转动跟不上平动,结果必然是平动轴与旋转轴之间的运动不协调,不协调运动又会产生机械冲击,加工工件时可能发生过切现象,影响加工表面质量和精度.为避免平动轴与旋转轴之间的运动不协调情况发生,本文增加对旋转轴的角速度及角加速度的动力学约束条件,提出如下旋转轴角速度、角加速度控制方法.
3.1 平动轴可达到的最大合成进给速度
经过第2小节的速度规划后,假设在第m个插补周期时,平动轴具有最大合成进给速度,本文中将其定义为Vm,根据前述分析,显然有Vm≤Vmax成立.以A-C型双摆头五轴数控机床为例,根据五轴线性插补原理可知,在第m个插补周期内有
(32)
成立.式中:Δlm为平动轴在第m个插补周期的合成位移;ΔAm为A旋转轴在第m个插补周期的角位移;ΔCm为C旋转轴在第m个插补周期的角位移;VAm为A旋转轴在第m个插补周期的角速度;VCm为C旋转轴在第m个插补周期的角速度.
式(32)中的旋转轴角位移ΔAm和ΔCm可按照以下线性比例进行分配获得:
(33)
式中:l为当前插补路径段的总长度;As为A旋转轴在当前插补路径段的起点坐标;Ae为A旋转轴在当前插补路径段的终点坐标;Cs为C旋转轴在当前插补路径段的起点坐标;Ce为C旋转轴在当前插补路径段的终点坐标.
式(33)中ΔAm和ΔCm分别与(Ae-As)和(Ce-Cs)取得相同的符号.
3.2 旋转轴角速度约束控制
由式(32)和(33)可知,平动轴在第m个插补周期达到Vm的进给速度时,A、C旋转轴角速度的绝对值也将分别达到最大值|VAm|和|VCm|,只要控制|VAm|和|VCm|均在机床旋转轴可承受的角速度约束范围内即可.
根据式(32)和(33),可推导出第m个插补周期内平动轴的合成进给速度Vm与A、C旋转轴的角速度VAm、VCm的关系式
(34)
假设五轴数控机床A、C旋转轴的最大极限角速度约束分别为VAmax和VCmax(机床旋转轴无论正转还是反转,角速度约束应恒为正值,即VAmax和VCmax均大于0).对A、C旋转轴角速度约束控制计算过程如下.
1)根据式(34)计算出VAm和VCm,将结果分别表示为
VAm=sgn(VAm)abs(VAm)
VCm=sgn(VCm)abs(VCm)
式中:sgn(x)为取x符号的函数;abs(x)为取x的绝对值函数.
2)当abs(VAm)≤VAmax且abs(VCm)≤VCmax时,表示A、C旋转轴的角速度均未超出机床旋转轴最大极限角速度,同时也表明此时的平动轴与旋转轴均可在各自允许的极限速度范围内协调运动,第2小节中关于平动轴进给速度的规划结果满足旋转轴角速度约束控制要求.
3)当abs(VAm)>VAmax或abs(VCm)>VCmax时,表示之前在第2小节里规划计算得到的实际可达到的平动进给速度偏高,使得至少有1根旋转轴的角速度已超出该旋转轴最大可承受的极限角速度,此时超出角速度约束范围的旋转轴将出现与平动轴运动不协调一致的情况.为此,需降低实际可达到的平动进给速度,使得对应的旋转轴角速度被约束控制在机床旋转轴最大极限角速度以内.对此,本文提出如下重新规划计算方法.
① 平动轴最大合成进给速度的修调
对1根旋转轴的角速度超出该轴角速度极限约束范围的情形(不妨设为A轴),可以sgn(VAm)VAmax代替式(34)中的VAm,可求得新的平动轴最大合成进给速度
(35)
同理对2根旋转轴的角速度均超出各自角速度极限约束范围的情形,分别以sgn(VAm)VAmax和sgn(VCm)VCmax代替式(34)中的VAm和VCm,求得
(36)
此时应取(V′m)A和(V′m)C中较小者作为新的平动轴最大合成速度V′m,即
V′m=min((V′m)A,(V′m)C)
(37)
式中min(x,y)函数为返回x和y中较小的数.
② 平动轴进给速度的重新规划计算
根据式(35)~(37)计算获得平动轴新的最大合成进给速度V′m后,将第2小节中Vmax重新赋值为V′m,对平动轴的进给速度进行重新规划计算.
3.3 旋转轴角加速度约束控制
假设五轴数控机床A、C旋转轴的最大极限角加速度约束分别为aAmax和aCmax(aAmax和aCmax均为正数),在整个加工过程中,实际最大角加速度应不大于aAmax和aCmax.在任意的第i个插补周期,旋转轴角加速度的计算公式为
(38)
式中ai为平动轴在第i个插补周期的加速度.
根据式(38)可知,旋转轴的角加速度与平动轴加速度之间具有线性相关性,即当平动轴具有加速度时,旋转轴同时也将具有角加速度,而且有
(39)
式中:(aA)max为A旋转轴实际的最大角加速度;(aC)max为C旋转轴实际的最大角加速度.
(aA)max和(aC)max(都取为非负数值).对式(39)的运算结果作如下讨论:
1)当(aA)max≤aAmax且(aC)max≤aCmax时,表示A、C旋转轴的角加速度均未超出机床旋转轴最大极限角加速度,同时也表明如按照机床平动轴最大极限加速度amax进行速度规划,其计算结果可以满足旋转轴角加速度约束控制的要求.
2)当(aA)max>aAmax或(aC)max>aCmax时,表示至少有1根旋转轴的角加速度已超出该旋转轴最大可承受的极限角加速度,此时表明第2小节中如果继续按照机床平动轴最大极限加速度amax进行速度规划,将导致旋转轴角加速度超出相应的最大极限角加速度约束范围.因此,需在进行平动轴速度规划前重新计算新的平动轴最大加速度amax,本文采用如下方法对平动轴最大加速度amax进行修调.
① 当1根旋转轴的角加速度超出该轴角加速度最大极限约束时(不妨设为A轴),可以(aA)max代替式(38)中的aAi,解得新的平动轴最大加速度
(40)
② 当2根旋转轴的角加速度均超出各自角加速度最大极限约束时,可分别以(aA)max和(aC)max代替式(38)中的aAi和aCi,求得
(41)
取式(41)中(amax)A和(amax)C的较小者作为新的平动轴最大加速度amax,即
amax=min((amax)A,(amax)C)
(42)
将式(40)~(42)计算出的amax作为平动轴进给速度规划时的加速度约束参数使用.
4 进给速度规划控制流程
综上所述,本文在第2、3小节中分别详细介绍了关于平动轴运动学约束控制方法和旋转轴的运动学约束控制方法.平动轴进给速度规划控制的约束条件为最大速度和最大加速度,旋转轴进给速度规划控制的约束条件为最大角速度和最大角加速度.在进给速度规划时,必须同时满足所有的约束条件,否则会对机床产生冲击或加工工件产生过切和欠切现象.因此,规划进给速度时必须对超限的速度或加速度参数进行重新计算.现将五轴数控加工时机床运动学参数约束条件下的进给速度规划控制流程(控制流程图如图6所示)归纳总结如下:
1)用式(39)计算旋转轴A/C的最大角加速度(aA)max和(aC)max.
2)若(aA)max≤aAmax且(aC)max≤aCmax
① 以平动轴的最大加速度amax进行速度规划,同时计算出平动轴最大合成速度Vm;
② 用式(34)计算A/C的最大角速度VAm和VCm;
③ 当abs(VAm)≤VAmax且abs(VCm)≤VCmax时,转入第4)步;
④ 当abs(VAm>VAmax或abs(VCm)>VCmax时,用式(35)~(37)计算V′m;
⑤ 令Vmax=V′m,转入第4)步.
3)若(aA)max>aAmax或(aC)max>aCmax
① 用式(40)~(42)重新计算平动轴的最大加速度amax;
② 转入第2)①步.
4)按照第2小节中的方法进行平动轴速度规划(见图5).
5 实际数据仿真与结果分析
为了验证本文提出方法的有效性,选取数控加工文件中的2个相邻程序段作为待插补路径段进行速度规划计算,如表1所示.

表1 相邻加工程序段数据
各类已知参数为:1)五轴数控机床相关的运动学约束参数,平动轴最大可承受的加速度amax=1 000 mm/s2,旋转轴的最大角速度为VAmax=VCmax=0.073 rad/s,最大角加速度为aAmax=VCmax=7 rad/s2;2)数控系统采样插补周期T=0.004 s;3)插补路径段起点线速度Vs=2 mm/s,终点线速度为Ve=4 mm/s;4)程序段指定的进给速度Vmax=12 mm/s.
使用本文提出的方法,平动轴合成进给速度曲线如图7所示.D点为预测加减速规划中的减速点,由于在速度规划中,周期数要进行取整,故实际的减速点并非D点,而是图中的D1点.理论减速点和实际减速点不重合,产生定位误差,导致实际不能达到插补路径段的终点,会产生残余位移,即图7中传统加减速规划速度曲线与本文加减速规划速度曲线所围成的面积.
为了避免产生残余距离,本文提出的方法可以提前规划好周期数,在规划好的周期内,将残余距离用一特定的速度分配到减速段的周期内,由于减速段每个周期都增加了一个速度,即在匀速段与减速段转接的这一周期加速度变小,其他周期加速度不变,因此本文的加减速规划控制方法不会导致加速度变大,该方法可不必预测减速点位置也能够精确到达插补路径段的终点,提高了位置控制精度.
以程序段指定的进给速度Vmax规划旋转轴的角速度、角加速度时,本文将旋转轴的最大极限角速度和最大极限角加速度作为速度规划的运动学约束条件.计算出的旋转轴角速度、角加速度若超出上述约束条件时,则以修改平动轴指定进给速度和最大可承受加速度amax的方式对进给速度进行重新规划控制,重新规划前后的旋转轴角速度曲线和角加速度曲线分别如图8、图9所示.
由修正前A轴角速度和角加速度曲线可知,A轴在修正前其角速度和角加速度都超出了旋转轴的最大角速度和角加速度限制,需要按照A轴的最大极限角速度和角加速度值来修正平动轴的指定进给速度和最大可承受加速度,修正后重新计算A轴的角速度和角加速度使其满足约束条件.由修正前C轴角速度和角加速度曲线可知,C轴在修正前其角速度和角加速度并没有超出旋转轴最大极限角速度和角加速度,但由于A轴的角速度和角加速度超限,重新规划使平动轴指定进给速度和最大可承受加速减小,同样也会使C轴的角速度和角加速度减小.
以满足旋转轴的最大极限角速度和最大极限角加速度约束条件的平动轴指定进给速度和最大可承受加速度来重新规划进给速度,重新规划前后的进给速度和加速度曲线分别如图10、11所示.可以看出修正后的进给速度和加速度都有所减小,这也将会增加插补周期数量.优点是有效避免了A轴对机床的冲击以及刀具对加工面产生的过切现象.
本文提出的加减速规划控制方法对五轴线性插补时的非线性误差的影响情况如图12所示.可以看出,在使用本文方法前的最大非线性误差为8,使用本文方法后的最大非线性误差为5,非线性误差降低了37.5%,表明本文提出的加减速控制方法仍能有效地提高加工表面的轮廓精度.
6 结束语
1)本文通过提前规划加减速周期,避免了预测减速点的难题,同时通过加工路径的前瞻运算,将剩余加工路径以某一速度平均分配到减速段的各个周期,从而使机床刀具精确地到达插补路径段的终点,提高加工精度.
2)分析传统旋转轴的速度按比例分配导致机床旋转轴会出现角速度、角加速度超过其最大值限制,机床不能平稳运动的问题,通过增加旋转轴的角速度、角加速度约束条件,提出速度修正算法来控制旋转轴的运动速度,从而使机床避免产生冲击,延长机床的使用寿命.
3)使用速度修正算法对平动轴的最大进给速度和最大加速度进行修正,通过Matlab软件进行实际数据仿真验证,非线性误差减小了37.5%,有效地提高了加工工件的精度.
